基于组合拍卖的城市能源系统共享储能运行方法
2022-09-19武昭原王剑晓李庚银
武昭原,周 明,王剑晓,李 昂,陈 琳,李庚银
(1. 新能源电力系统国家重点实验室(华北电力大学),北京市 102206;2. 中国华电集团有限公司,北京市 100031)
0 引言
在“双碳”目标的驱动下,构建以新能源为主体的新型电力系统已成为未来能源电力的发展形态[1]。大量分布式可再生能源的接入给城市能源系统的灵活高效运行带来了新的挑战,以分布式储能为代表的具有快速响应能力的需求侧灵活性资源得到了广泛关注。但实际中,分布式储能的进一步应用仍然存在着一系列限制:1)从成本可竞争性角度而言,当前储能设备投资成本较高,而城市能源系统中,分布式储能仍然缺少合理的成本疏导机制,投资回报周期长;2)从电网调度角度而言,相对于大电网传统运行模式,目前城市能源系统中分布式储能接入及出力具有布局分散、可控性差等特点,若任其自发运行,相当于接入一大批随机性的扰动电源,其无序运行不仅无助于电网频率、电压和电能质量的改善,还会造成储能资源的浪费[2-4]。
在此背景下,有学者提出了共享储能的概念以消除传统分布式储能“独享”模式所带来的初始投资高、利用率低等缺陷[5-7]。共享储能可理解为共享经济与电力系统储能的融合,用户通过支付服务费用随时随地按需使用由集中式或大量分布式储能聚合构成的共享储能资源[8-10]。
近年来,针对不同的应用场景,已有不少关于共享储能运营模式方面的研究[11-13]。其通用思路为建立多元市场主体与储能的协同优化运行模型,并以此为基础,量化评估储能共享的价值,设计激励性的交易和结算机制。文献[14]提出了针对分布式光伏用户间的储能共享应用场景,量化评估了城市能源系统中的共享储能模式的潜在效益。文献[15]提出了点对点交易模式下适应储能共享的整体框架。在此基础上,文献[16]聚焦于储能共享使用权的拍卖问题,基于拉格朗日方法实现了不同应用场景中对储能功率和容量使用权的定价,尽可能挖掘储能的共享潜力。
考虑到储能共享与传统电能量交易的不同,储能使用权的拍卖是不可分割的,不同用户对于共享储能的需求是一个确定的充放电功率和容量的组合,文献[17-18]从组合拍卖的视角研究储能的共享问题。需要注意的是,共享储能的组合拍卖是典型的非确定性多项式困难(non-deterministic polynomial hard,NP-hard)问题,其计算复杂度将随着参与者的增加呈指数级增长。在实际城市能源系统多元应用场景中,大量的储能资源潜在需求者可能使得共享储能组合拍卖存在计算瓶颈。针对上述问题,文献[19-20]分别提出了完全多项式时间的近似算法和智能算法,用于实现组合拍卖问题的快速求解。然而,其组合拍卖依赖于各市场成员投标的预期收益作为竞胜标决定的标准,仅局限于需求侧的峰谷价差套利这一应用场景,泛化能力有限,难以适应面向多应用场景的实际城市能源系统需求。其中,多应用场景指的是共享储能适用于提供调峰、调频等不同辅助服务,应用场景的局限将限制共享储能组合拍卖的实际价值。
为解决当前城市能源系统中储能共享所面临的难题,本文针对面向多应用场景的共享储能组合拍卖机制展开研究。建立了考虑共享储能多维参数耦合的组合拍卖模型,考虑到共享储能组合拍卖的计算复杂度问题,提出了基于共享储能多维参数稀缺性的贪婪算法。为激励各市场成员真实披露自身的共享储能租赁需求,设计了基于捆绑定价的共享储能使用权支付机制。算例结果表明,在大规模市场成员参与下,本文所提的基于共享储能多维参数稀缺性的贪婪算法在实现组合拍卖的高效求解的同时,能够保持较高的经济有效性,并兼容多元化的共享储能应用场景,具有较强的实用价值和可扩展性。
1 基于组合拍卖的共享储能运营模式框架
一般而言,储能的运行主要包括储能充放电、储能容量、电量净变化值以及充放电效率等参数。共享储能运营商面临的是如何依据各市场成员的差异性需求,将共享储能参数进行最优分配的问题。由于储能的充放电功率和容量存在协同耦合特性,必须同时获得相应使用权的分配才有意义。因此,共享储能运营的本质为组合拍卖问题。本文构建了如图1 所示的基于组合拍卖的共享储能运营模式以实现共享储能资源在不同时段的最优分配。

图1 基于组合拍卖的共享储能运营模式Fig.1 Operation mode of shared energy storage based on combinatorial auction
共享储能的运营主要涉及3 类市场成员:
1)共享储能运营商:负责组织共享储能拍卖、收集和匹配各共享储能竞拍者的报价,并根据拍卖结果对共享储能进行分配和结算。共享储能的分配涉及各运行时段的储能容量、充放电功率以及储能存储的能量的多维度资源分配,且各资源间存在耦合特性。因而,其本质为一类组合拍卖,在中国目前的市场中,可由电网运营商或第三方聚合商承担这一职能。
2)储能使用者:即共享储能拍卖中的买方,需要根据自身需求和预期收益,向共享储能运营商提交相应的报价,且报价形式需要满足组合拍卖的相应要求。
3)储能提供方:即共享储能拍卖中的卖方,实际中,储能提供方可以是规模较大的集中式储能。在城市能源系统中,共享储能大多体现为单体容量较小的分布式储能资源。
本文重点关注分布式储能聚合后的共享储能分配问题,即对应组合拍卖为单边拍卖的形式,未考虑储能提供方的具体形式。需要强调的是,本文所提出的基于组合拍卖的共享储能运营方式具有很强的适用性,能够扩展为考虑不同类型和规模共享储能提供方参与的双边组合拍卖形式。
2 共享储能分配模型
2.1 组合拍卖报价
在共享储能的组合拍卖中,由于储能容量、充放电功率等多维参数的耦合特性,竞标者仅能获得单一的参数(例如仅得到储能容量而缺少相应的功率)是没有意义的,竞拍者需要根据自身需求对各运行时段共享储能的参数标的物组合进行报价投标,具体的投标形式为:

2.2 竞胜标决定模型
本文所提的共享储能运营模式指的是由单一运营商统一管理共享储能。首先,需要由各共享储能买家提交相应的投标信息。然后,共享储能拍卖商根据所有投标信息确定共享储能的分配方案,即竞胜标决定问题。模型中不同用户的共享储能报价为已知,竞胜标决定模型的核心在于确定共享储能多维参数的最优分配方式。因此,模型中并不涉及网络约束的问题。其表达式为:


在竞胜标决定模型中,目标函数式(3)依照组合拍卖报价,以全社会福利R最大为目标;式(4)表示组合拍卖报价中标信息的约束;式(5)至式(7)分别表示共享储能报价所涉及的充电功率、放电功率以及容量的中标总和不能超过相应的共享储能限值;式(8)和式(9)分别为共享储能的SOC 方程和相应的SOC 约束,即要求共享储能各时段总的中标参数应满足相应的储能运行物理约束。
需要注意的是,在本文所提的共享储能分配问题中,仅考虑确定性的分配方案,即yn,s为二进制变量,某一市场成员申报信息对应的共享储能参数要么全部满足yn,s=1,要么不分配任何参数(即yn,s=0),不存在部分满足的情况。
2.3 求解算法
针对基于组合拍卖的共享储能分配模型可等效为带约束的多维0-1 背包问题,是典型的NP-hard 问题,难以求出最优解。在实际中,当参与共享储能租赁的市场成员数量较多时,采用常规的优化求解算法将难以得出有效的分配方式。以0-1 背包问题为例,不同问题规模下精确求解方法的计算复杂度如附录A 图A1 所示。其中,C1 和C2 分别对应枚举法和动态规划法,而C3 对应物品可拆分的情况,即将0-1 约束松弛后采用冒泡排序法求解。
对于共享储能组合拍卖问题而言,其精确算法的计算复杂度将随市场参与成员的增加呈指数级增长。对比M2 和M3 可知,组合拍卖竞胜标决定模式计算复杂度主要是由于组合拍卖无法拆分,需要供需一一匹配。因此,为了降低竞胜标问题求解的时间复杂度,需要牺牲一定的分配效率,只有用牺牲拍卖微小的经济效率来对标施加某些限制,才能顺利实现组合拍卖,即采取折中的方式,在牺牲一定精确度的条件下快速得出近似的最优分配方案。
为此,本节提出了基于资源稀缺度的贪婪算法求解思路。通过辨识不同组合拍卖报价在共享储能分配中的优先级对其进行排序,实现在多项式时间内求解的同时,尽可能保证所得的结果更接近最优值。各个共享储能竞标者需要提交的投标信息包含标的物和相应的竞标价格。对于共享储能运营商而言,某个共享储能竞标的吸引力不仅取决于投标人对单位储能资源愿意支付的价格,还会受不同时段共享储能资源稀缺性的影响,即在某些储能资源稀缺时段,需要对应相对更高的支付价格。因此,将资源稀缺度通过等效的投标单位表示,投标优先级表达式为:

根据储能不同参数的物理属性可知,当电价较低时,即此时电能供给相对充裕,市场成员更倾向于将能量存储。因此,可以认为充电功率比放电功率更有价值,反之亦然。对于储能容量而言,这一属性是实现电能时空转移的必要条件,易知储能容量的价值在电价波动性较强的场景下价值更高。综上所述,电价与共享储能不同参数的价值有很强的关联性,可以作为很好的稀缺性表征指标,特别是在共享储能试点初期,采用外生表征电能稀缺性的指标也有助于保证共享储能运营模式的稳定发展。基于这样的思路,共享储能各维度参数的稀缺度表达式为:

式中;λt为t时刻日前市场的出清电价,共享储能运营商可根据实际情况将其替换为其他可表征电能稀缺性的指标或参数;NT为ΦT对应的总出清时段数。
相比于单纯依赖共享储能投标的方式,在共享储能不同参数的稀缺度与外生表征电能稀缺度的指标间建立了联系,能有效降低潜在的策略性投标行为,用于求解共享储能的组合拍卖模型的贪婪算法伪代码详见附录B。
所提的贪婪算法可以在多项式时间内求出一个近似解,具有较高的求解效率。定理1 能够进一步说明贪婪算法在共享储能组合拍卖求解中具有较好的适用性。
定理1:给定任一单时段形式为[Qω,i,bi]的共享储能组合拍卖报价向量,若对于所有竞拍者满足Qω,i≤φQmax,且φ∈(0,0.5],仍然可以使得贪婪算法所得的近似解最低精确度提升至1-φ。其中,Qω,i和bi分别为第i次组合拍卖报价中关于共享储能参数类型ω的申报量和价格,Qmax为共享储能该参数类型的总量,φ为比例系数。定理1 的证明如附录B 所示。
3 共享储能定价及结算机制
共享储能运营商依据各共享储能买家提交的申报信息确定中标的报价,对所分配的共享储能资源进行定价和结算。共享储能竞胜标决定问题旨在优化储能资源的分配效率,而共享储能定价及结算则决定了资源分配的公平性[19]。
合理的定价和结算机制能有效引导市场成员披露自身真实的偏好、优化共享储能资源分配方式、提升社会福利。一直以来,Vickery-Clarke-Groves(VCG)机制被认为是能抑制策略性竞价的有效方式。然而,考虑到共享储能的组合拍卖问题需要通过近似算法进行求解,在近似算法难以保证最优解的特点将使得VCG 机制难以保障满足激励相容的特性。此外,VCG 机制本身有极高的计算复杂度,并不适用于共享储能的组合拍卖定价。
为此,本文采用了基于捆绑式定价的结算机制。基于前述计算出的尝试从市场成员的组合报价中提炼出共享储能的单位价格,考虑到共享储能运营商可能存在自身的保留价格或共享储能投资成本,且共享储能所带来的社会福利理应由双方共享,本文将社会福利在共享储能运营商和储能买家之间均分,具体的定价机制表达式为:

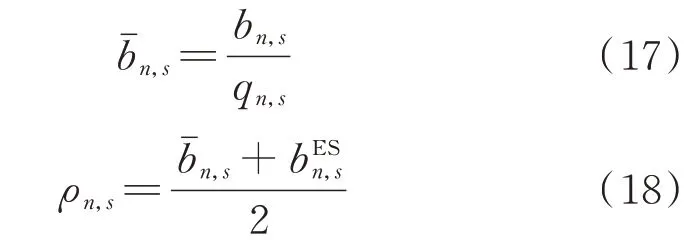
式中:ζn,s为第n个组合拍卖参与者提交的第s次储能组合拍卖报价中所申报的参数占总参数的比例;qn,s为第n个组合拍卖参与者提交的第s次组合拍卖报价申报的储能各参数不同时段的总等效参数;bˉn,s为第n个组合拍卖参与者提交的第s次组合拍卖报价中单位储能参数的报价;bESn,s为共享储能运营商与bˉn,s匹配的保留价格,该保留价格呈分段上升的趋势;ρn,s为第n个组合拍卖参与者提交的第s次组合拍卖中对应报价的单位结算价格。
这种定价机制本质为各共享储能买家与共享储能运营商分段式保留价格的一一匹配。这样的形式一方面符合常见的供给函数形式,另一方面也更契合未来考虑供需双向组合拍卖的共享储能运营模式。不仅如此,对于某组合拍卖参与者而言,谎报信息的动机在于,若虚报低价后依然可以中标,则可以降低结算价格,进而使得自身获得超额收益。不同于常规的单边拍卖可以由拍卖组织者获得全部的社会福利,上述结算机制中考虑了共享储能运营商对储能拍卖权的保留成本,最终的结算价格取保留成本和市场成员报价的平均值,降低了拍卖参与者对结算价格的操纵能力。不仅如此,考虑到共享储能的保留价格为分段上升的形式,对于某个市场成员而言,其谎报信息的行为会降低自身组合拍卖投标的优先级。一方面,会导致自身的投标匹配较高的保留成本,使得最终结算价格升高;另一方面,在极端场景下可能导致无法中标的结果,造成更为严重的效率损失。这将在算例分析中进一步量化分析所提结算机制对潜在策略性报价的抑制作用。
4 算例分析
4.1 算例设置
为便于表示,在基础算例中,只考虑1 个共享储能运营商和10 个共享储能买家,拍卖时段为6 个,共享储能的容量为10 MW·h,充放电功率限值为5 MW。基础算例中的各申报信息和对应的物理含义如附录C 所示。在4.3 节中,将进一步分析拍卖时段为下一运行日以小时为单位的24 个时段中考虑大规模市场成员参与下的共享储能组合拍卖效率。其中,共享储能容量和充放电功率极限值分别为50 MW·h 和50 MW,各维度参数的稀缺度所依据的日前市场出清价格取自美国PJM 电力市场。
为了说明本文所提组合拍卖求解算法的合理性和有效性,设置了如下3 个对比场景:
1)M1(基准场景),在本场景中,将采分支定界法求解共享储能组合拍卖模型,以获得相应组合拍卖的理论最优解;
2)M2(对比场景),在本场景中,将采用本文提出的基于共享储能多维参数稀缺性的贪婪算法求解组合拍卖模型,从而在多项式时间内得到一个近似最优解;
3)M3(对比场景)[20],在本场景中,将采用常规的基于单位参数价值的贪婪算法求解共享储能组合拍卖模型,相比于M1 和M2 中的方法,M3 未考虑不同时间段共享储能资源价值的差异性。
4.2 共享储能组合拍卖结果分析
根据附录C 表C1 所给出的各市场成员共享储能组合拍卖申报信息以及各时段市场价格,不同场景下的报价优先级以及中标情况图2 所示。其中,M1、M2 和M3 对应的组合拍卖报价总和分别为101、101 和93 元。

图2 不同场景下报价优先级及中标情况Fig.2 Quotation priority and winning bids in different scenarios
对比图2 中M2 和M3 下的结果可以看出,由于不同的近似算法对报价优先级评估的差异性,导致最终不同的中标结果,主要体现在对于组合拍卖报价序号8 和9 之间优先级排序。具体来看,尽管报价8 和9 的价格一样,其差别在于,报价8 所申报的储能参数较高,但涉及的时段较少。而M3 中仅考虑到报价8 所申报的储能参数仅涉及前2 个时段,总量较小,而忽略了前2 个时段储能供电功率较为稀缺。因此,错误地优先选择了报价8,导致报价3 无法中标,进而使得最终社会福利的降低。
从另一方面看,本文提出的基于稀缺性的贪婪算法能够较好地考虑不同时段储能各个维度参数的稀缺性,进而更容易得到更优的组合拍卖结果,在本例中也直接导致了最终结果的差异性。不仅如此,在图2 中,M2 和M3 对于报价3 和7 也呈现了相反的优先级排序结果,相比于报价7,尽管报价3 申报的储能参数较高,但其大部分参数都在储能资源较为富裕的时段或是充裕度较高的参数。因此,在M2下的报价3 优于报价7。
需要注意的是,在本例中,M2 的中标情况与理论最优结果一致,但这可以理解为个例。尽管大多数情况下基于稀缺性的贪婪算法(M2)结果会优于M3,但相比于理论的最优情况(M1)还是有一定的差距。
4.3 共享储能组合拍卖效率分析
事实上,在组合拍卖机制设计中,始终存在着拍卖的经济效率和竞胜标计算复杂性这一固有的矛盾,当共享储能组合拍卖市场成员增加时,其计算复杂度将大幅度提高。本节定义了组合拍卖的经济有效性(Economic efficiency,EE)指标,用来衡量组合拍卖结果与理论最优的社会福利的差异性,即近似算法所得的组合拍卖社会福利(M2 或M3)和理论最优社会福利(M1)的比值。
不同规模市场成员参与下组合拍卖模型的求解速度和EE 指标如图3 所示。其中,横轴表示组合拍卖的参与规模,纵轴分别表示M1 和M2 下的计算时间,M3 计算时间与M2 类似,此处不再赘述。注意不同市场成员参与情况下所对应的共享储能参数也等比例扩大,为了避免出现4.2 节中单次实验的偶然性,对各组场景均进行了10 次模拟,最终结果为10 次模拟的平均值。
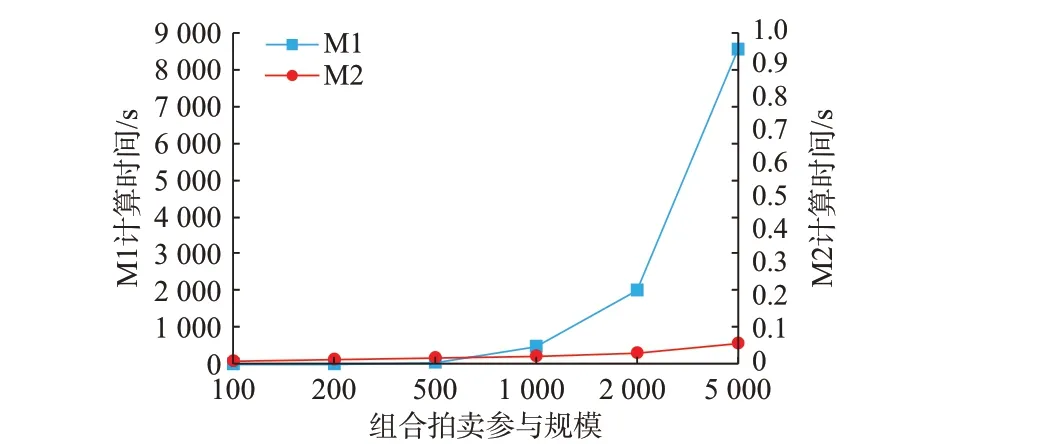
图3 不同规模市场成员参与下组合拍卖模型的求解速度和经济有效性Fig.3 Solving speed and economic efficiency of combinatorial auction model with different scales of market member participation
对比图3 中不同共享储能组合拍卖参与规模对应的计算时间可以明显看出,M2 下的计算时间非常短,仅随市场成员的增加而略微有所上升。这主要是由于贪婪算法本身对应较低的计算复杂度,增加的时间主要为市场成员增大对应的优先级排序时间的增加。相比之下,M1 的分支定价法决策空间随着市场成员的增加而呈指数级增长,相应的计算时间大幅度增加。此外,随着市场成员的增加,M2对应的EE 指标也呈现稳步增长的趋势,这主要是由于共享储能资源随着参与规模增加而等比例扩大,相应的共享储能资源充裕性提高,间接增强了贪婪算法的有效性,M2 下各次模拟仿真结果的EE 指标详见附录C 图C1。
随着市场成员参与规模的增加,M2 和M3 下组合拍卖的经济有效性如图4 所示。可以明显看出,随着共享储能组合拍卖参与规模的不断扩大,M2和M3 下的EE 指标差异呈现逐渐增大的趋势。这主要是由于大规模市场成员参与降低了个别极端情况的可能性,保证了时段间储能需求的差异性,这一结果与图3 中的EE 指标变化趋势也是一致的。需要指出的是,M2 和M3 下的EE 指标与实际的组合拍卖申报信息和稀缺性指标的取值有关,在某些情况下会存在M2 社会福利低于M3 的情况。

图4 M2 和M3 下组合拍卖的经济有效性Fig.4 Economic efficiency of combinatorial auctions in M2 and M3
4.4 报价行为的激励相容性
本节将重点分析共享储能组合拍卖中参与者报价行为的激励相容性。激励相容性用来衡量市场成员如实报价的意愿,即市场成员是否有动机偏离自身对所需要共享储能资源真实的评估值从而获得更高的收益。对于组合拍卖参与者而言,可尝试选择低于自身真实需求的报价,从而获得更高的效益。具体可分为以下3 种情况:
情况1:由于报价过低,导致自己未中标,此时对应的效用为0。
情况2:由于报价相对较低,对应较低的报价优先级,结算时与较高的共享储能保留价格配对,反而使得最终结算价格比真实报价高。
情况3:与情况2 类似,但此时尽管与较高的共享储能保留价格配对,但最终结算价格仍然相对较低。此时,用户可获得超额收益。
鉴于上述各类情况的可能性,本节为量化分析市场成员报价行为对结算结果的影响,引入了比例系数,以表示市场成员报价偏离真实值的比例。例如:比例系数0.9 表示市场成员组合拍卖报价为真实值的90%。以基础算例中中标的5 个组合拍卖报价为切入点,分析不同报价行为对应的收益情况,考虑到图2 中的报价4 优先级极高,小幅度降低报价并不影响组合拍卖结果,此处重点分析剩余的4 组报价。不同报价行为下对应的收益偏差率如图5 所示。其中,蓝色方块代表策略性报价带来了一定的收益增长率,红色方块则为策略性报价导致的收益损失率。
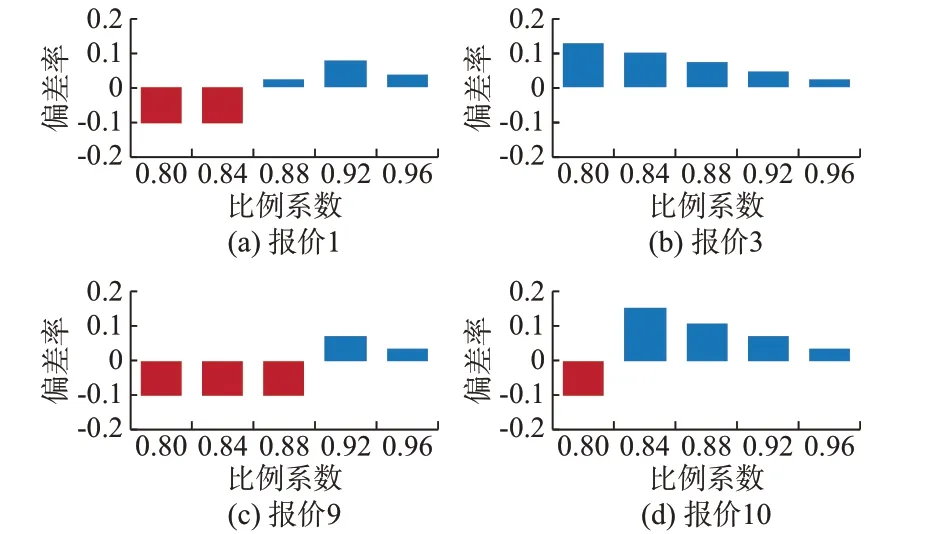
图5 不同报价行为下的收益偏差率Fig.5 Benefit deviation rate with different quoting behaviors
由图5 可知,除报价3 外,其余报价均可能由于策略性报低价而导致不中标,进而使得效用直接将为0,即情况1。如图5 中红色方框所示,报价1 还可能因为降低报价而导致优先级降低,与较高的共享储能保留价格配对,进而导致效用降低,即情况2。本文所提的交易结算机制能在一定程度上抑制策略性报价行为。对于本例中的报价3 来说,中标是因为其申报信息对应的储能资源恰好较为充裕。因此,即便是较低的价格也可以中标,这一现象也是符合市场价格规律的。随着组合拍卖参与规模的扩大,不同报价优先级差异缩小时,共享储能组合拍卖竞争性更充分时,本文所提的组合拍卖结算机制将可能呈现更强的激励相容性。
5 结语
针对当前城市电力系统中储能资源利用率不足、缺少有效投资回收路径问题,本文围绕面向多应用场景的城市电力系统共享储能组合拍卖机制展开研究,建立了考虑共享储能多维参数耦合的组合拍卖竞胜标决定模型。考虑到共享储能组合拍卖具有较高的计算复杂度,设计了不同时段储能资源稀缺性的量化指标,进而构建了基于共享储能多维参数稀缺性的贪婪算法。为激励各市场成员真实披露自身的共享储能租赁需求,设计了基于捆绑定价的共享储能使用权支付和结算机制。算例结果表明:
1)相比于传统的组合拍卖求解算法,本文所提的基于共享储能多维参数稀缺性的贪婪算法能够将求解速度提升90%以上。
2)相应求解算法能够保持较高的经济有效性,求解精度稳定保持在90%以上,当市场成员参与规模较大时,求解精度可接近95%,具有较好的实用价值。
3)所提的交易结算机制能在一定程度上抑制可能的策略性报价行为,提升资源配置的效率。
本文针对的是日前时间尺度下的确定性共享储能单边组合拍卖问题,后续将进一步研究电动汽车、需求响应等存在不确定性的广义储能共享问题。同时,在实际系统中考虑网络约束对不同地理位置广义储能共享的影响,提出相应的共享机制、效益评估方法和求解算法。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
