基于尖峰脉冲的气体冲击系统研究

2022-09-19李雯牛秦玉畅科剑蒙松

机床与液压 2022年5期

李雯，牛秦玉，畅科剑，蒙松

(西安科技大学机械工程学院，陕西西安 710054)

0 前言

冲击能和冲击频率是气压冲击装置的重要输出参数，当气体冲击系统产生较大的尖峰脉冲时可达到最佳的工作效果。利用气体冲击系统在产生冲击能的条件下，通过匹配其相关影响因素，达到产生大量尖峰脉冲的目的，进而可合理利用尖峰脉冲来击碎细小血栓。深静脉血栓(Deep Vein Thrombosis，DVT)主要是因为血液在静脉腔内不正常的凝结导致的。当深静脉形成血栓后，若未及时有效干预会向肺栓塞发展，导致患者死亡。血栓很难使用药物疗法或通过手术进行彻底溶解治疗，因此早期预防非常重要。

为实现冲击系统的高频快速冲击，产生较大的尖峰脉冲，对气体冲击系统建立数学模型并进行仿真，研究其动态特性。

1 气体冲击装置

1.1 脉冲治疗的原理

气体冲击系统是通过充气气囊有次序、有规律地进行充气膨胀挤压、放气，形成对肢体组织的循环压力，如图1所示。根据机械的间歇式加减压作用，促进深静脉系统的血液循环，致使凝血因子无法聚集而无法粘附在血管内壁，改善血液和淋巴循环，增加纤溶系统的活性，加快局部代谢产物和炎性物质的清除，提高皮肤表面细胞温度，达到活化血管的目的，可有效防止肌肉萎缩、消除水肿、预防深静脉血栓。因此，气体冲击系统产生的间歇式脉冲根据气体的冲击效果不同，治疗效果也大大不同。

图1 使用压力治疗仪体内血液循环效果

1.2 气体冲击装置的工作原理

该系统采用单双腿的工作模式，并且每个气囊分为3个气路，分别为近端、中端和远端气路，如图2(a)所示。系统在工作过程中，为实现气体冲击过程的快速打开和关闭，选用电磁阀控制气体的充放过程。先由压力传感器检测气缸内压力是否为0，若为0 则启动气泵，然后控制核心可对近端气路的充气阀通电，进行充气。当气缸内压力达到设定值的50%时，充气阀2断电关闭，第一路进入保压状态；压力传感器4再次检测气缸内部压力，若保压状态正常，则关闭气泵，再次打开充气阀，气囊5进气，延时脉宽时间；滞后几秒后关闭充气阀，打开放气阀3，延时间歇时间，装置模型和单气路工作状态分别如图2(b)和表1所示。如此重复上述步骤进行间歇式脉冲加压，充气频率最高30 s一次，通过脉冲气体产生的气体冲击来击碎细小血栓，加快血液流通，骤然减压使得血液回流充盈。如此循环间歇，相比于一次充放气效果更显著、利用率更高。每一轮完成后再继续新一轮循环，左右腿可同步独立进行工作，直到达到设定的治疗时间即停止工作。

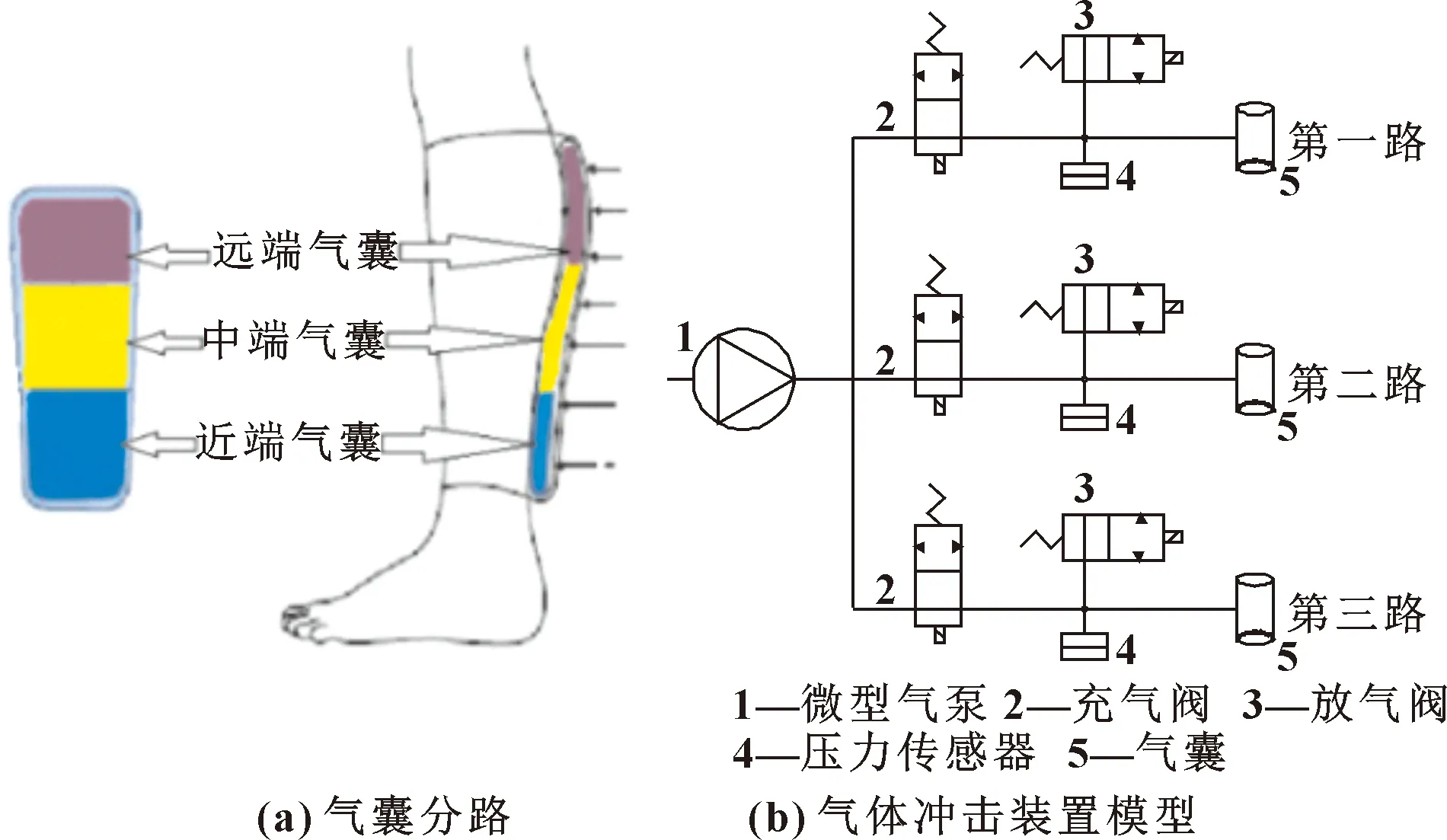
图2 气囊分路及气体冲击装置的工作原理

表1 单气路的工作状态

1.3 尖峰脉冲的产生原理

气体冲击的工作原理是将具有一定压力和流量的气压通过阀控缸系统转换为具有一定速度和冲击力的机械动能。因此气压冲击可以利用高压气体的释放来形成强大的冲击力，从而产生机械动能或者其他形式能量瞬间的传递和转化。当脉冲气体被瞬时释放时处于高压状态，产生强烈的冲击，这种状态下的气流在管道内的流动表现为湍流，质点的运动很不规则，相互碰撞混掺，速度和压力在空间和时间上具有随机的脉动性质。

在间歇式脉冲加压过程中，需要不断打开和关闭充放气阀，以延时脉宽时间，充气频率最高为30 s一次。打开充气阀给气缸内充气，当气缸内压力达到设定值的50%时，关闭充气阀，气缸内压力处于保压状态，一段时间后，在打开排气阀的瞬间，气缸内部气体释放造成压力骤然下降，产生短暂而强烈的气体冲击，冲击力随脉冲传播呈周期性变化，当冲击力达到峰值时，治疗部位受力最大，此时气体所产生的短暂高频脉冲称为尖峰脉冲，一段时间后压力下降，此时关掉排气阀，气体处于稳定状态并且产生一段时间的恒压值。随着再次打开充气阀重复上述步骤，气体的冲击力逐渐减弱，直至降压过程中达到下一个尖峰脉冲，由此脉冲气体的冲击力可以根据治疗时间呈周期性变化，从而产生多个尖峰脉冲使得治疗效果尽可能达到最佳。

2 气体冲击过程的数值模拟

为分析系统各元件参数对于冲击性能的影响，实现参数优化，对气体冲击装置进行动态分析，计算系统在产生气体冲击过程时的气缸内部压力变化曲线；通过分析模拟气缸压力变化过程，推导出压力计算公式，并进行模拟试验，验证模拟试验系统的可行性。由于在脉冲加压过程中，打开排气阀释放气体时间较短，因此气体冲击过程也很短暂，可以认为此过程绝热。

2.1 气体冲击的数学模型分析

在该系统工作过程中，理想气体状态方程与真实情况有偏差，考虑到计算结果的准确性和方程复杂程度，采用-状态方程计算气体参数。-方程形式为

(1)

式中：为物质的摩尔体积。

当气体混合物间没有相关反应产生时，将它作为纯净物质，根据统计热力学，用数学式表示混合气体的系数与各组成气体的系数之间的关系。对于种气体组成的混合气体，文中气体为空气，和是与气体种类有关的系数，表示反应分子间的相互吸引力，表示无法自由活动的空间，只和其体积相关。因此，和取自HEIDEMANN和PRAUSNITZ等的研究成果：

(2)

(3)

式中：为通用气体常数；为临界温度；为临界压力。

对于截面积为的管道，其流动状态由管道的两端压力之比决定。临界状态下排气管出口和进口截面上的气体压力之比称为临界压力比，用=/表示。临界压力比由公式(4)得出：

(4)

式中：为理想气体比热容。临界压力比仅与等熵指数有关，对于空气选定=1.40，则=0.528。

此时临界状态下的流速为

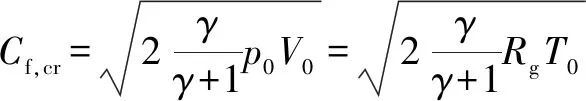
(5)

式中：为上游气体压力;为上游气体温度；为上游气体体积。

由上式可得临界流速决定于进口的状态，、或的大小影响着临界状态下的流速大小。由连续性方程可得出口截面单位面积的气体流量为

(6)

式中：为出口截面单位面积的气体流量；为出口截面面积；为下游气体体积。

将流速公式和定熵过程参数关系式代入上式得：

(7)

式中：为下游气体压力。

当>时，流动为亚声速，由理想气体多变过程关系式和等熵流动关系式得到质量流量′ 的表达式，其结果可以定性地应用于真实气体：

(8)

式中：为上游气体密度。

当≤时，即使降低下游压力也不能增大流动速度，此时流动壅塞，流动速度为声速，质量流量为

(9)

实际上，当气体流经复杂的内部元件时，产生的损失是不可以忽略的。在上游和压差条件确定的情况下，实际通过元件的质量流量将小于按理论公式计算出的理论质量流量。引入流量系数(0<<1)，以表征由于摩擦等耗散因素引起的流动速度的减少，则实际质量流量为

(10)

流量系数可以根据Perry试验近似计算：

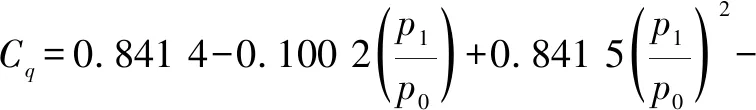
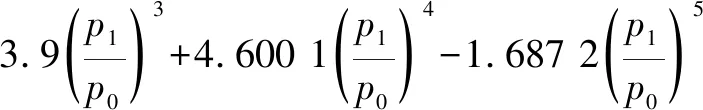
(11)

气缸内的压力变化可由开口系统的能量方程计算：

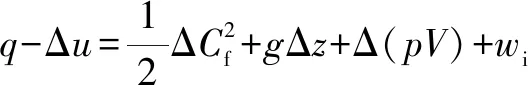
(12)

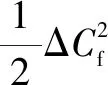
若认为过程绝热，略去热传递、摩擦损失、气体重力势能项，则充放气过程中气缸内能的变化量等于流入与流出气体焓的变化量，即：

d+d=d

(13)

内能=、焓=，其中可通过定值比热容来计算，而/=。

2.2 数值计算参数设定

系统在进行脉冲加压过程时，由于间歇式加压充气频率最高为30 s一次，当打开排气阀时，气缸内部产生气体冲击，从而产生短暂的尖峰脉冲。此后一段时间内，气缸内部的压力处于均匀状态，假设这段时间压力达到平衡，则可以利用该时间段内气缸内部的气体流量，通过开口系统能量方程计算气缸内部压力的变化。

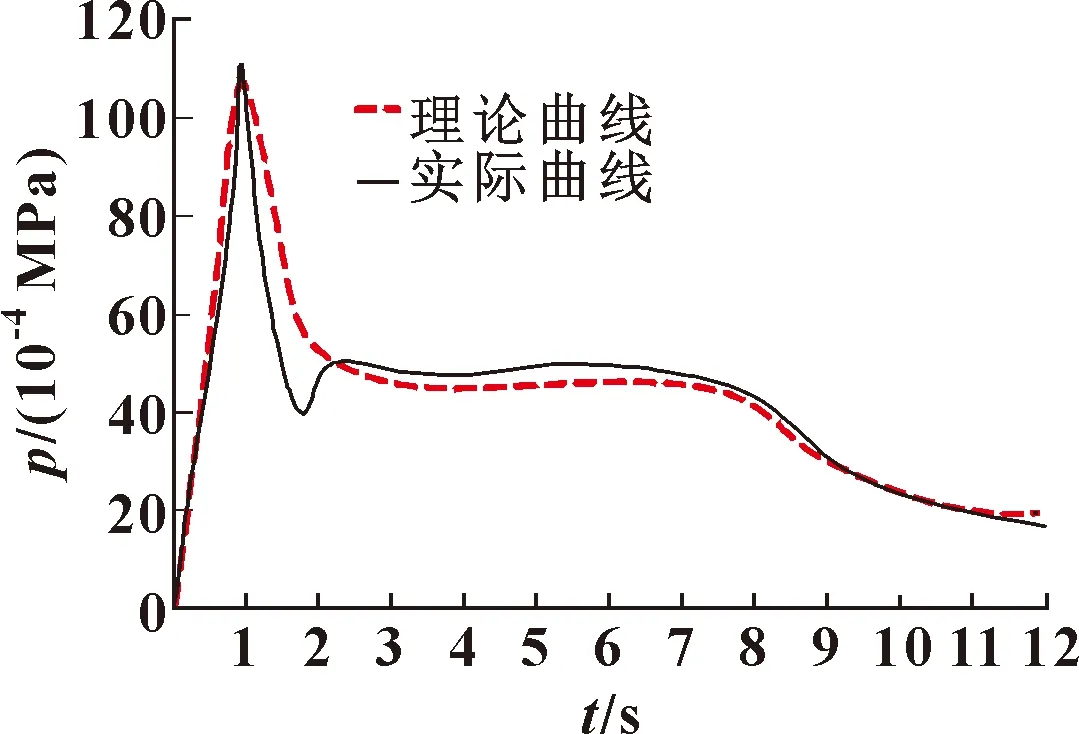
图3 气缸内部压力曲线

根据上述气体冲击数学模型分析，设定仿真参数，通过 MATLAB软件进行仿真计算，运行仿真模型，模拟间歇式脉冲加压过程中产生尖峰脉冲时气缸内部压力变化情况。其中，计算的主要参数：气泵的初始压力6×10MPa，气缸容积2 L，管道直径20 mm，排气口面积30 mm。根据上述计算结果得到的曲线和实际测得的曲线对比如图3所示。

3 气体冲击装置的仿真试验

由于该系统的气体冲击装置简化模型和数值计算会产生一定的误差，并且根据气体冲击的工作原理可得，该系统需要通过脉冲气体被瞬时释放从而产生强烈的冲击来形成尖峰脉冲。因此，需要分析不同的相关参数对于尖峰脉冲产生过程的影响，从而指导试验系统参数的设定和调试。

气体冲击系统中的气体冲击装置主要包括微型气泵、气缸、控制进排气开关的电磁阀、进排气导管以及气囊。可得尖峰脉冲气体的产生受多种因素的影响，如包括微型气泵的初始压力、气缸容积、电磁阀口径大小、排气口面积和管道直径。考虑到整个抗血栓治疗系统样机在安装好之后，再改变其中各个参数不便，并且耗费成本。因此，采用MATLAB软件进行仿真试验，来验证各个参数的改变对尖峰脉冲产生的影响。在对各个单因素进行分析时，采用控制变量法，保证其余各参数不变，通过试验测试得到最佳的一组数据。规定试验测试的基准参数：微型气泵的初始压力为6.00×10MPa、气缸容积为2 L、管道直径为20 mm、排气口面积为30 mm。

(1)微型气泵的初始压力参数对尖峰脉冲的影响

该系统通过微型气泵给气缸内部充放气，因此改变气泵的初始压力，会影响气缸内尖峰脉冲气体产生的峰值和恒压值。考虑到抗血栓设备主机的便携轻巧性，其应考虑内部各个元器件实际体积大小，以及额定功率和电压等参数。因此，设置微型气泵的初始压力分别为0.05、0.06、0.07 MPa，进行仿真试验，得到尖峰脉冲压力曲线如图4所示。可得：随着气泵的初始压力增大，尖峰脉冲的压力峰值到达时间滞后，峰值压力减小，下降斜率基本无影响，稳压状态下的恒压值增大。

(2)气缸容积对尖峰脉冲的影响

改变气缸容积，设置其容积分别为1、2、3 L，进行仿真试验，结果如图5所示。可以看出：随着气缸容积的增加，尖峰脉冲的压力峰值到达时间滞后，峰值压力增大，下降沿变陡，稳压状态的恒压值基本不变。

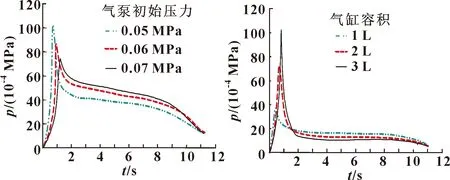
图4 微型气泵初始压力对尖峰脉冲的影响图5 气缸容积对尖峰脉冲的影响

(3)电磁阀口径大小对尖峰脉冲的影响

该系统采用电磁阀作为控制气路的开关，分为充气阀、放气阀和控制微型气泵的开关。若要产生尖峰脉冲，则需要电磁阀在通电和断电的同时响应速度极快，才能形成压差，产生短暂而强烈的气体冲击。因此，采用SMC_VX2系列直动式电磁阀，其特点是响应速度快、动作时间很短且频率较高，在真空、负压、零压时都能正常工作。分别取该型号电磁阀的口径为2、3、5 mm进行仿真试验，结果如图6所示。可以看出：随着电磁阀的口径增大，尖峰脉冲的压力峰值到达时间提前，峰值压力增大，下降沿变陡，稳压状态的恒压值减小。

(4)排气口面积对尖峰脉冲的影响

该系统是间歇式脉冲加压，需要通过重复进排气来延时间歇脉冲时间，从而产生多次尖峰脉冲，并且整个治疗过程需要一定的气压保压状态来维持脉冲效果，因此排气口的面积不宜过大。设置排气口的面积分别为20、30、40 mm，进行仿真试验，结果如图7所示。可以看出：随着排气口面积的增加，尖峰脉冲的压力峰值到达时间滞后，峰值压力增大，下降斜率增大，稳压状态的恒压值增大。

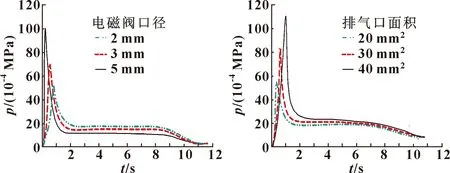
图6 电磁阀口径大小对尖峰脉冲的影响图7 排气口面积对尖峰脉冲的影响

(5)管道直径对尖峰脉冲的影响

改变管道的直径，设置其直径分别为10、20、30 mm，进行仿真试验，结果如图8所示。可以看出：随着管道直径的增加，尖峰脉冲的压力峰值到达时间提前，峰值压力增大，下降沿变陡，稳压状态的恒压值减小。

图8 管道直径对尖峰脉冲的影响

4 样机试验系统调试

经过设计加工后，得到气体冲击系统样机如图9所示。考虑理论计算的误差，仿真试验过程中各个参数的影响程度和实际调节的难易程度等因素，最终确定试验系统参数为：微型气泵的初始压力为6.00×10MPa、气缸容积为2 L、管道直径20 mm、排气口面积40 mm、电磁阀口径为5 mm。为测试尖峰脉冲产生的过程中延时间歇时间的最佳参数，编制相应的软件控制界面进行试验。

图9 气体冲击系统样机

在开机后，系统会向串口屏发送信号，开机成功后串口屏显示LOGO，此时页面跳转至参数设置界面，并且启动气泵使其压力达到设定值的50%，系统开始检测电路是否正常工作，若正常则判断工作模式，可由用户自己设定单双腿工作模式；若没有正常工作，则报故障。

本文作者设计的治疗系统可以选择足部或腿部进行治疗，在参数设置页面中可以设定相关的治疗压力。在参数设置完成后，根据用户选择的治疗部位，该治疗系统开始工作。此时判断气囊内气压为0后，打开进气阀，关闭排气阀，并且启动气泵充气，到达设定的时间后，再次判断气囊内部压力，若为0，则报故障；若不为0，则重复上述步骤，直到达到预设的压力。此时，关闭微型气泵和进气阀，打开排气阀，延时脉宽间歇时间，利用充放气时产生的尖峰脉冲可达到较好的治疗效果，重复上述步骤，达到治疗预设时间自动停止，完成整个工作过程。

根据设定好的参数，按照上述系统的工作流程，以近端和远端气囊为例，模拟系统治疗加压过程，通过软件控制界面显示尖峰脉冲曲线，分别如图10和图11所示。

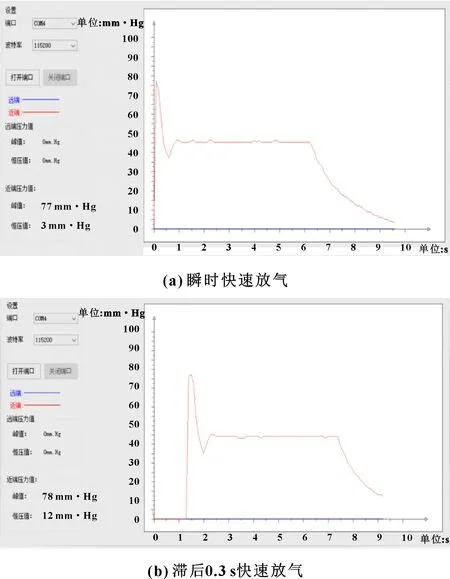
图10 近端气囊尖峰脉冲压力曲线

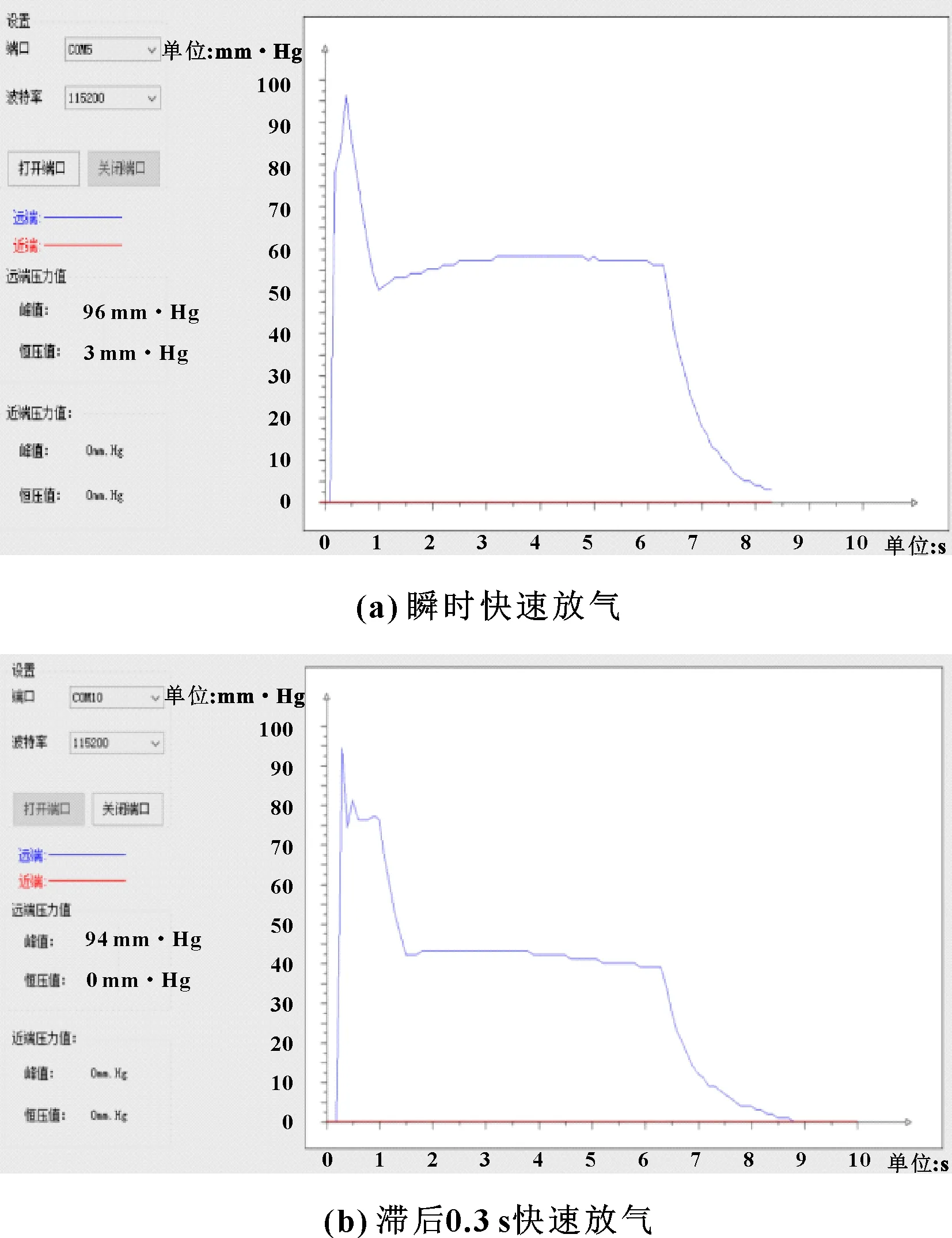
图11 远端气囊尖峰脉冲压力曲线

由图10、图11可以看出：近端气囊尖峰脉冲压力可达到1.04×10MPa(78 mm·Hg)、远端气囊可达到1.28×10MPa(96 mm·Hg)，与理论计算结果相比，主要区别是下降沿更陡，并且恒压值较大，产生略微振荡；随着排气阀的突然打开，气缸内产生瞬时气体冲击，因此形成尖峰脉冲值在9.33×10～1.47×10MPa(70～110 mm·Hg)，随着气体的排出，压力减小，一段时间后，关闭排气阀延时间歇时间，让气缸内部气压趋于稳定，在5.33×10～6.67×10MPa(40～50 mm·Hg)，此时到达恒压值。