直角切削剪切角与剪切带有限元仿真分析

2022-09-19丁宇星俞建超鲁治锴

机床与液压 2022年16期

丁宇星，俞建超，鲁治锴

(福州大学机械工程及自动化学院，福建福州 350100)

0 前言

有限元方法是研究切削过程中应力、应变和温度分布的有力方法。对于剪切角，国内外大量学者都对其作出了不同程度的深入研究。目前应用最为广泛的是MERCHANT根据最小能量原理得出的剪切角公式以及LEE和SHAFFER根据最大剪切应力与主应力方向呈45°夹角所得到的剪切角公式。然而，由于Merchant与Lee-Shaffer的剪切角预测模型都是在一些简化模型上建立起来的，没有考虑刀具以及材料的影响，并且实际切削加工过程更为复杂。因此，其预测模型所求得的剪切角往往与实际剪切角有较大出入。林海龙通过实验测得的主切削力，利用能量平衡方程，并结合SEETHALER和YELLOWLEY所提出的摩擦角计算方法，对45钢的剪切角进行了合理的预测；并与Merchant与Lee-Shaffer的剪切角公式所得到的结果进行对比，发现Merchant公式计算结果偏大，而Lee-Shaffer公式计算所得到的剪切角偏小；并得出了随着切削速度增大、剪切角增大的结论。ZVORYKIN进行了大量直角切削实验，通过拟合实验数据，得到了Zvorykin剪切角经验计算公式；但由于Zvorykin公式中的待定常数对于不同材料有着不同的值，并且没有较好的理论解释，因此并未得到广泛应用。郭建英利用有限元方法，对比Zvorykin公式以及其他公式所得到的剪切角，认为在实际工程应用中，有限元数值模拟方法与Zvorykin公式都是较为准确的剪切角预测模型。刘勇等人利用有限元方法研究了铝合金211z.1的剪切角，并修正了Merchant公式。WANG等也利用有限元方法研究了单晶铜各向异性的剪切角。

对于第一变形区剪切带宽度的研究，也有许多结论。CHIFFRE通过快速停刀试验，认为剪切带厚度为切削厚度的一半，其结论也被广泛应用。SHI等建立了剪切带厚度的解析模型，并结合试验结果与仿真模型进行了对比分析；但由于其涉及到的变量过多，求解过程过于复杂，因此并未得到广泛应用。GRZESIK考虑到剪切带的厚度与切削深度和剪切角有关，认为随着切削厚度的增大，剪切带宽度增大；随着剪切角的增大，剪切带宽度减小，并建立了相应公式。实际上，GRZESIK所建立的剪切带模型，是基于剪切带长宽比为10的假设。在实际切削加工中，剪切带长宽比会随着切削条件的变化而改变。MOLINARI等在研究钛合金锯齿形切屑时，也总结了相应的剪切带厚度公式。然而目前对于第二剪切带的研究较少。

LALWANI等基于解析模型，建立了不依赖于实验结果求解剪切角、第一和第二变形区剪切带厚度的解析模型。通过刀屑接触面的流动应力与平均剪切应力相等、刀尖点的正应力与刀屑接触面的平均正应力、切削力最小原理来分别约束剪切角、第一变形区剪切带长宽比以及第二变形区厚度系数。其模型的特点在于：将第一变形区与第二变形区作为一个整体进行分析，并考虑了加工硬化对剪切角的影响，但也忽略了第二变形区剪切应变对切屑厚度的影响。剪切角、剪切带是研究切削机制的重要途经。对于剪切角与剪切带的测量，可以通过制作切屑根部的金相来获取，且精度较高。但切屑根部金相制备过程极为复杂。相比之下，有限元方法则更容易获得剪切角、剪切带以及应力、应变、应变率、温度等相关数据。

本文作者通过Deform2D建立直角切削模型，分析第二变形区剪切应变对切屑厚度的影响，从而建立了新的剪切角求解模型；并探究了第一和第二变形区剪切带厚度与切削速度、切深的关系。

1 仿真模型与方案

本文作者旨在利用有限元方法探究剪切角、剪切带与切削速度、切削深度的关系，因此材料本构模型、物理参数皆取Deform2D内置参数。选取Al6061_Machine(JC)为工件材料，刀具材料选择Coating-AlO涂层刀具。环境温度设为20 ℃，刀屑接触面传热系数设为45 W/(m·K)，摩擦因子设为0.6。刀具前角、后角都为5°，刃口半径为0.01 mm。采用Deform自适应网格划分，材料分离准则为Nomalized Cockcroft & Latham准则。Al6061_Machine(JC)部分内置应力应变曲线如图1所示，材料物理参数如表1所示。

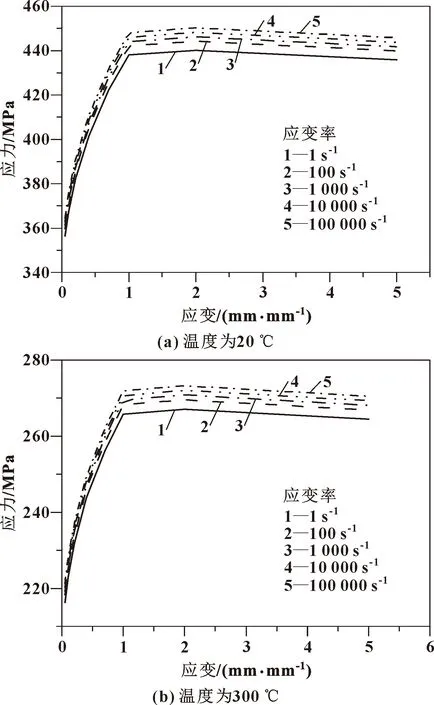
图1 部分应力应变曲线

表1 Al6061_Machine(JC)材料属性

选取切削速度为50、100、200 m/min，切削厚度分别为0.5、1、2、2.5 mm。加工参数组合如表2所示。

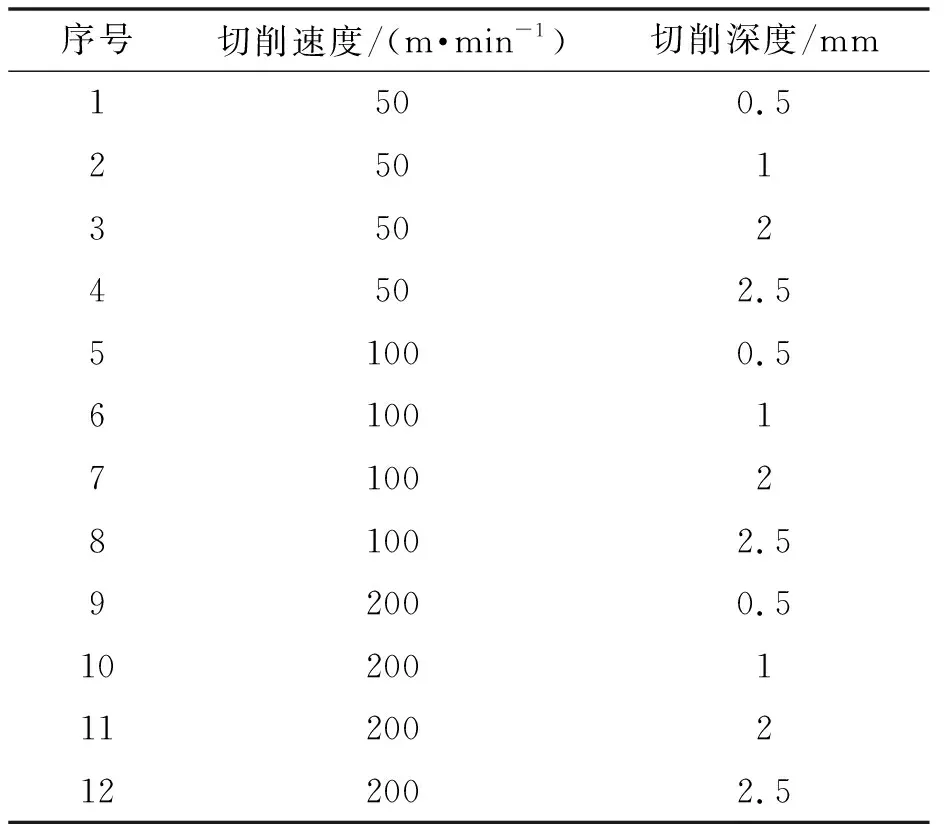
表2 加工参数

2 仿真结果与分析

通过Deform后处理程序量取剪切角、剪切带。剪切角通过剪切带长度与切削厚度计算得到。第一变形区厚度通过应变率分布图来确定。分别沿着垂直于剪切带的方向，在不同位置设置3条路径，通过应变率分布来确定第一变形区的厚度。最后取3条路径上厚度的平均值作为最终剪切带厚度，如图2所示。第二变形区厚度通过应变分布图来确定。在刀屑接触面分别取不同的3点，沿着垂直于刀屑接触面的方向设置3条路径，根据路径上的应变分布来确定第二变形区厚度，并取平均值作为第二变形区厚度，如图3所示。

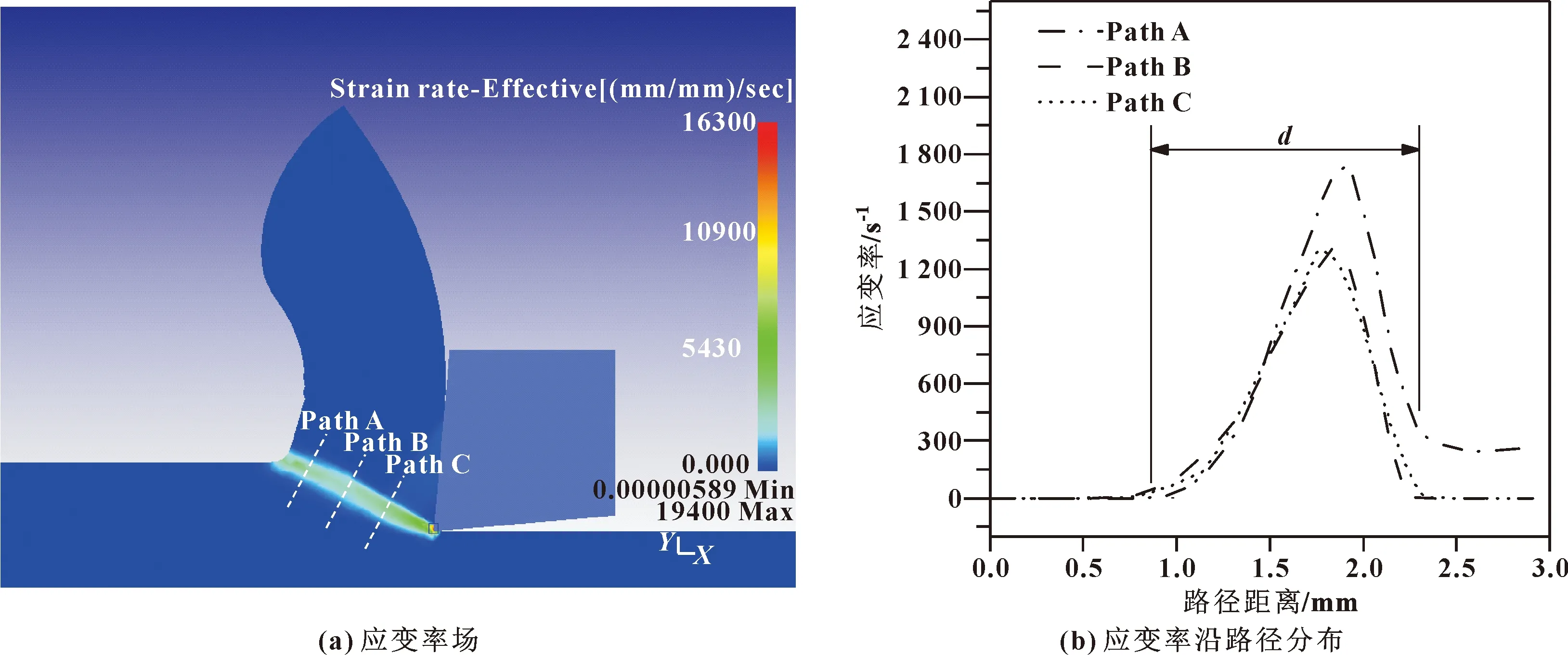
图2 确定第一变形区厚度

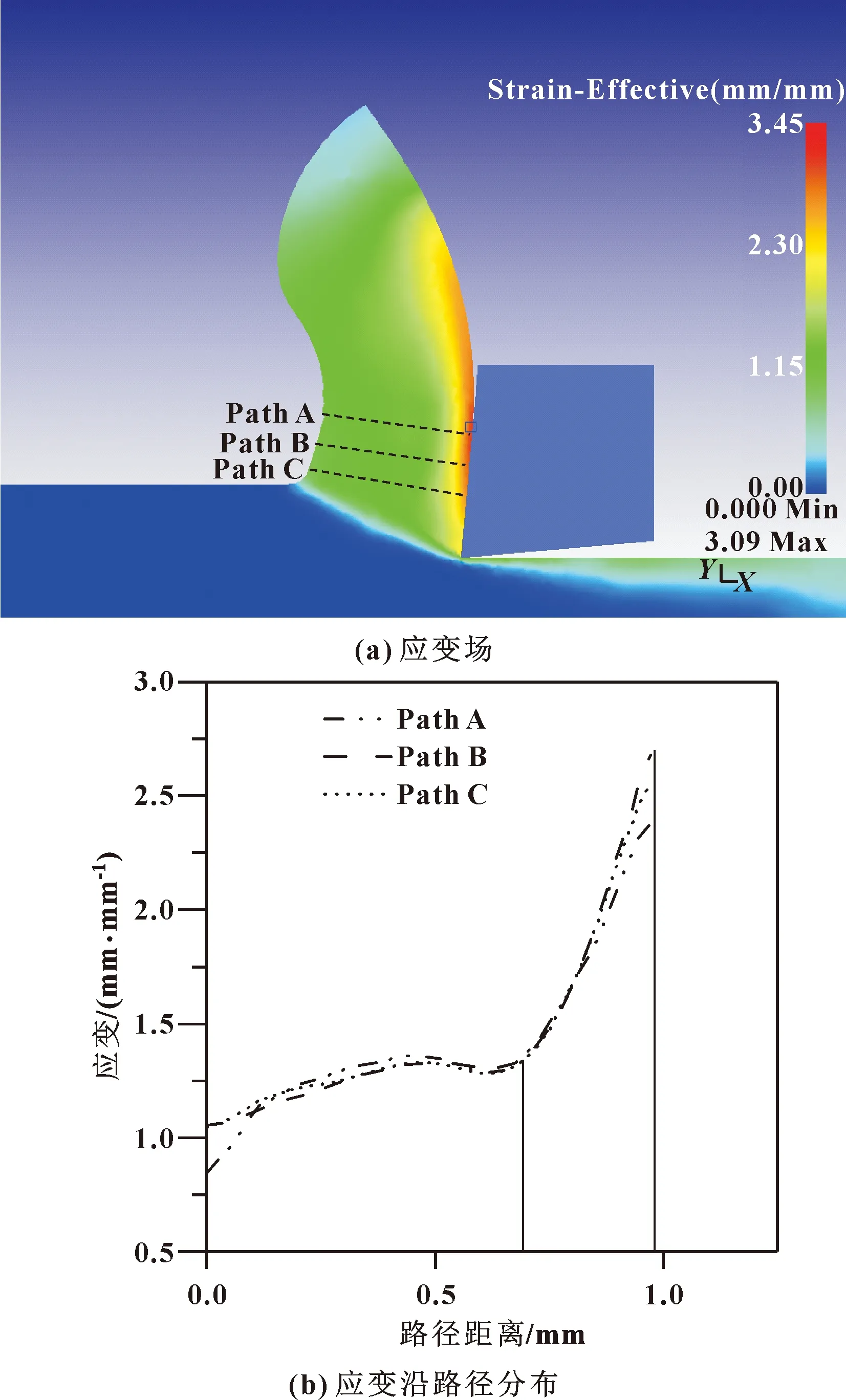
图3 确定第二变形区厚度

2.1 剪切角分析

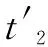
图4 剪切二维模型

(1)

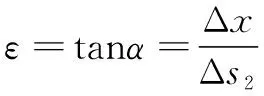
(2)

因此，在考虑第二变形区剪切应变的情况下，提出了新的剪切角计算公式，如式(3)所示：

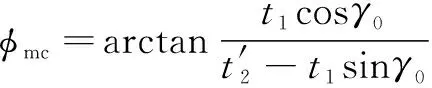
(3)

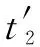
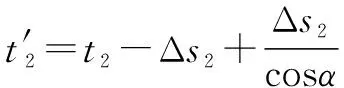
(4)

联立式(2)—(4)得到最终修正的剪切角如式(5)所示：

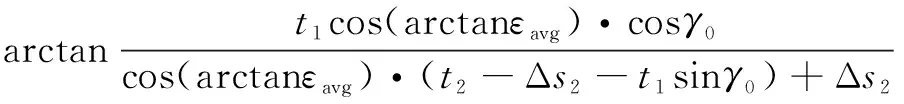
(5)

应当注意的是：第二变形区的剪切应变非均匀分布，因此采用平均剪切应变。平均剪切应变可以由Deform后处理界面测量，假设应变沿着刀尖点到刀屑分离点线性增加，通过刀尖点和刀屑分离点应变值差的一半作为平均剪切应变。图5为测量剪切角与不同模型计算所得剪切角对比。通过计算得到的误差为4.15%，的误差为2.12%。

图5 不同模型剪切角与测量剪切角

根据OXLEY平行剪切带模型，主切削力的计算公式如式(6)所示。

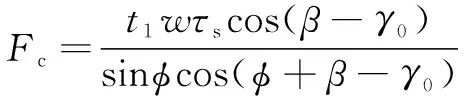
(6)

式中：为切削宽度；为剪切应力；为摩擦角。大量的切削实验表明，剪切带最大应力不随切削条件而改变，只与材料参数有关。MERCHANT根据最小能量原理，假设剪切面的剪切应力不变，求得剪切角公式如式(7)所示：

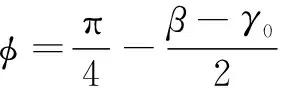
(7)

SCHULZ根据实验数据总结出关于切削速度与摩擦因数的经验公式，如式(8)所示：

(8)

其中：为常数；<0；为切屑流出速度。根据式(7)—(8)可知，随着切削速度增加，切屑流出速度增大，摩擦因数减小，摩擦角减小，剪切角增加，这与仿真结果相符。

将式(7)代入式(6)，得到关于摩擦角与切削力的关系式(9)：

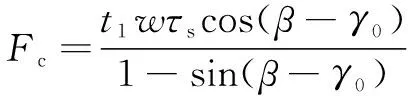
(9)

可以看出：随着摩擦角增大，减小。结合式(8)可以得出结论：随着切削速度的增加，摩擦因数减小，主切削力减小。图6显示了不同切削厚度下，切削速度与主切削力和剪切角的关系。

图6 不同切削厚度下切削速度与主切削力和剪切角的关系

2.2 第一、第二剪切带分析

图7是剪切带厚度在不同切削速度下与切削厚度的关系。对于第一变形区，从图7(a)可以看出，剪切带厚度随着切削厚度的增加而增加，这与CHIFFRE和GRZESIK的结论相符。但切削速度对剪切带厚度的影响较小。根据前述结论，切削速度增加，剪切角增加。结合GRZESIK认为剪切角增加、剪切带厚度减小的结论，应当有切削速度增加、切削厚度增大的结论。然而仿真结果表明，剪切带厚度与切削速度并无明显的单调关系，这与GRZESIK的理论相违背，即剪切带长宽比不为定值。对剪切带厚度与切削厚度进行线性回归拟合，得到式(10)：

图7 不同切削速度下不同切削厚度与剪切带厚度的关系

Δ=0484-0042

(10)

可以看出剪切带厚度约为切削厚度的1/2，这与CHIFFRE的结论相符合。

对于第二变形区的剪切带厚度，可以通过OXLEY扩展模型的迭代得到。但由于迭代过程过于复杂，难于找出第二变形区厚度与切削要素和材料性能的直接关系，因此建立第二变形区厚度与切削厚度、切削速度拟合关系更具有实际意义。从图7(b)可以看出：剪切带厚度主要与切削厚度有关，随着切削厚度的增大而增大。切削速度影响较小且并无明显单调关系。因此，可以假设第二变形区剪切带厚度仅与切削厚度有关，对其进行线性回归拟合，得到式(11)。

Δ=0519-0061

(11)

可以看到，第二变形区厚度也约为切削厚度的一半。