基于改进瞬时刚性力模型的机床铣削加工监测

陈璜，林雄萍

(1.集美大学诚毅学院实验管理中心，福建厦门 361021;2.集美大学诚毅学院机械工程系，福建厦门 361021)

0 前言

快速准确的切削力预测是提高数控机床立铣削加工效率的必要条件。目前主要有3种切削力预测方法：基于正交切削数据的能量分析方法、基于有限元法的解析模型和瞬时刚性力模型。前2种方法均能准确预测切削力，但需要大量的时间和精力进行分析。瞬时刚性力模型在实际应用中更加常见，这是因为与其他2种方法相比，它可以用较少的计算时间以合理的精度预测切削力。然而，传统的瞬时刚性力模型需要6个切削系数来预测切削力。每个刀具和工件组合都需要预先从切削实验中确定切削系数，仍需要较多时间和精力。因此，该技术在真实工厂中的应用十分困难。

一些研究者尝试减少切削参数的数量来优化瞬时刚性力模型。MOUFKI等将平头立铣刀的螺旋角视为斜切削时的倾角，从而使用斜角切削模型来预测切削力。LIN等在斜角切削模型的基础上对瞬时刚性力模型进行了改进，以便更容易地预测切削力，减少了所需切削系数的数量，并且只需通过一次初步实验测得的切向切削力就可以确定切削系数。然而，上述方法的参数识别仍然需要一个初步的实验。此外，还存在一个关键问题，它们均没有考虑刀具跳动引起的旋转半径偏差。因此，在有刀具跳动的情况下，以上方法无法准确预测切削力。

因此，本文作者改进切削力预测模型，以消除对初步实验的依赖，并考虑刀具跳动，实现无需任何力传感器测量的切削力预测。所需参数在铣削操作开始时根据主轴电机扭矩确定。此外，刀具跳动会导致切削刃出现不同的未切削切屑厚度，因此可以通过检测未切削切屑厚度之间的差异，精确预测切削力。通过实验，验证所提模型的有效性和先进性。

1 切削力预测模型及切屑检测方法

1.1 基于斜角切削模型的切削力计算

根据传统的瞬时刚性力模型，所提模型中的刀具被表示为一堆微小的圆盘元件。瞬时刚性力模型如图1所示。

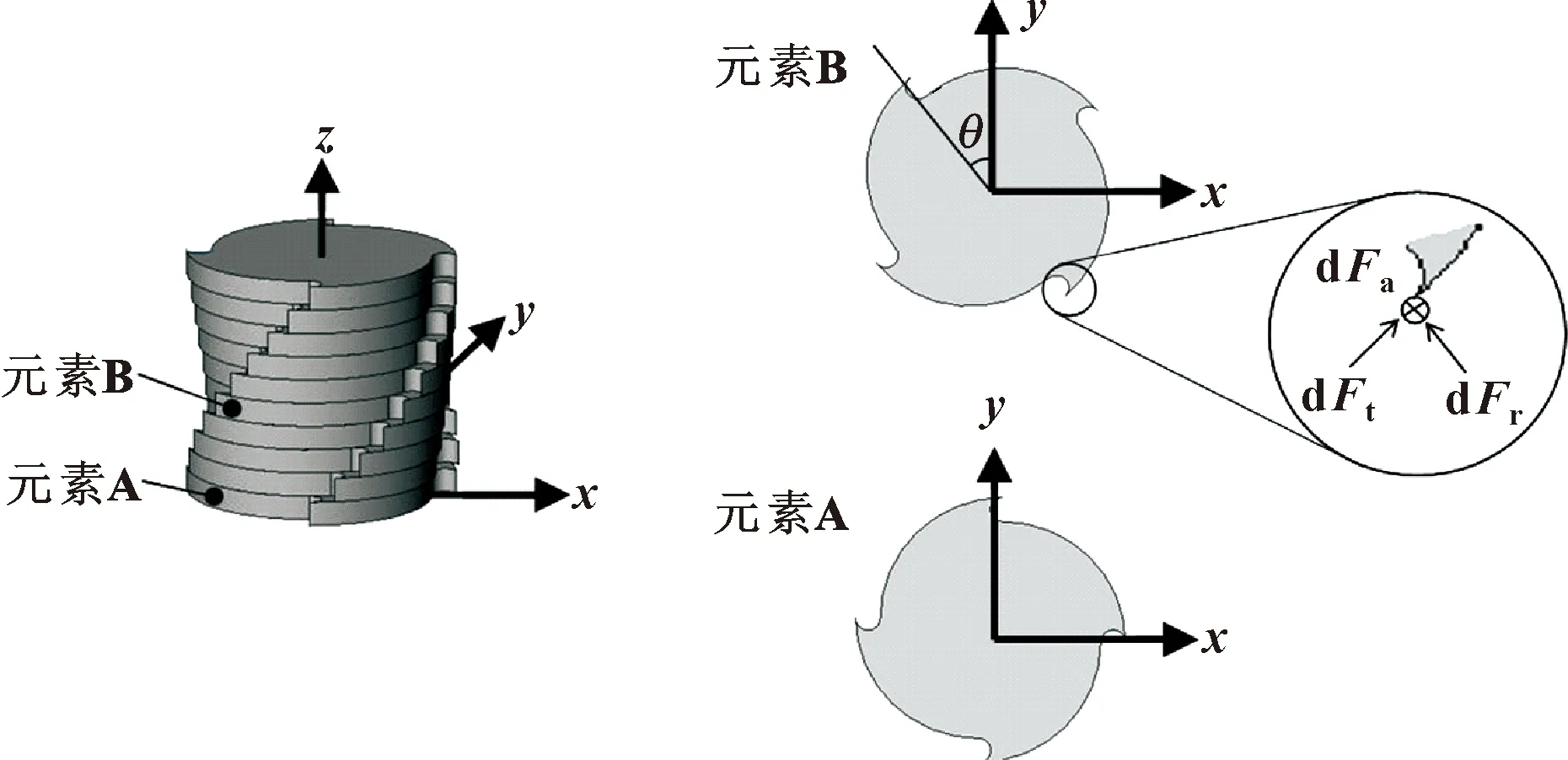
图1 瞬时刚性力模型

如图1所示，在传统的瞬时刚性力模型中，需要利用初步实验确定的6个切削系数计算作用在每个圆盘单元上的微小切削力。相比之下，所提出的模型采用斜角切削模型(见图2)计算微小切削力。在斜角切削模型中，平头立铣刀的螺旋角用倾角表示。计算切削力所需的参数如表1所示。

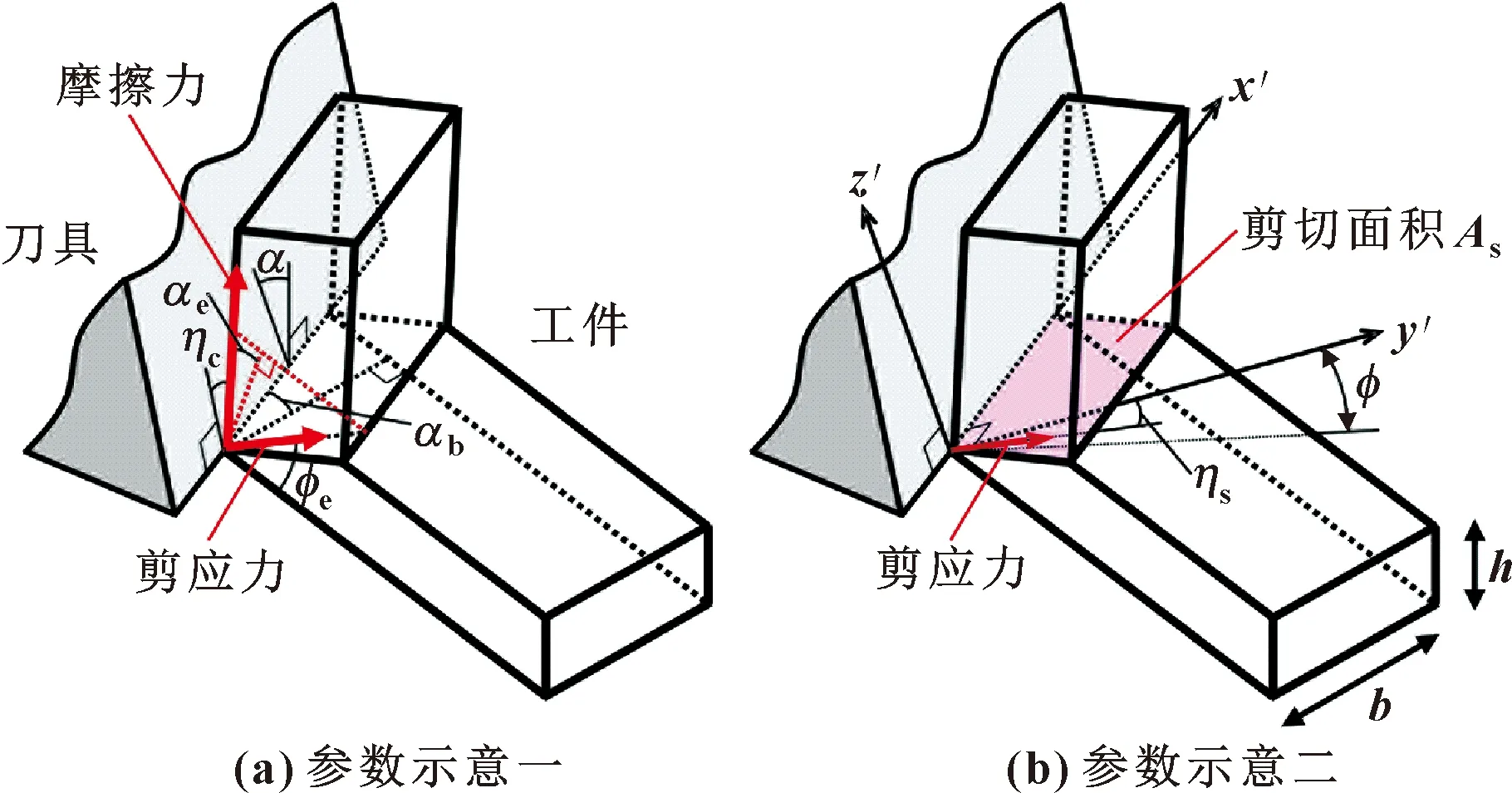
图2 斜角切削模型

表1 斜角切削模型中的参数

为减少模型中所需的参数，文中进行如下假设:

(1)采用最大剪应力理论估计剪切方向，在该理论中，剪应力最大的方向为剪切方向；

(2)根据现有研究中的一些假设，用于计算切屑流动角的公式为

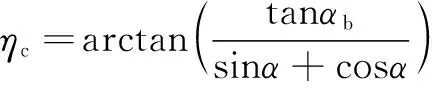
(1)

因此，除了剪切角和切屑流动角，表1中给出的其他参数都可通过几何关系计算。剪切角是该模型中唯一需要的参数，与传统瞬时刚性力模型需要6个剪切系数相比，该模型所需参数数量明显减少。

1.2 考虑刀具跳动的每齿进给量分析

现有基于斜角切削的瞬时刚性力模型将切削刃轨迹近似为一个圆弧，这是因为每个齿的进给量比刀具半径小得多。因此，未切削切屑厚度()的几何计算公式为

()=sin

(2)

式中：为每齿进给量；为刀具旋转角度。

刀具跳动导致切削刃有不同的未切削切屑厚度，现有的模型没有考虑由刀具跳动引起的旋转半径偏差。因此，切削力的偏差表示需要改进。

文中刀具跳动的影响是利用旋转半径的变化来模拟的。因此，考虑刀具跳动的每齿进给量如图3所示。

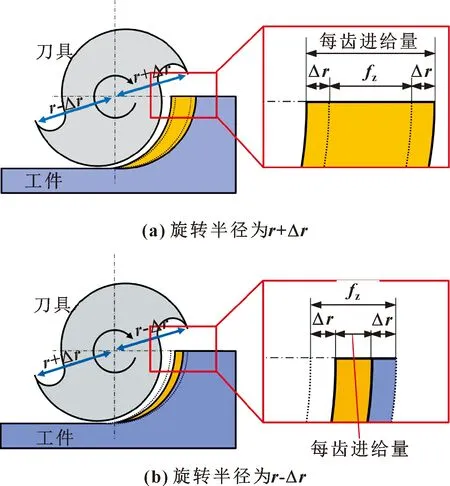
图3 考虑刀具跳动的每齿进给量

在图3中，为旋转半径、Δ为刀具跳动引起的偏差，Δ可通过千分尺测得。旋转半径偏差为Δ时，每齿进给量在每个切削刃处的变化为±2Δ。因此，考虑刀具跳动的未切削切屑厚度计算公式变为

()=(±2Δ)sin

(3)

1.3 剪切角的确定

如上所述，所提出的模型中需要的唯一参数是剪切角。根据能量守恒定律，从主轴电机扭矩中识别出剪切角。用于识别剪切角的参数如表2所示。

表2 用于识别剪切角的参数

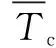
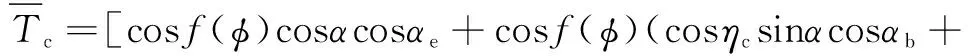
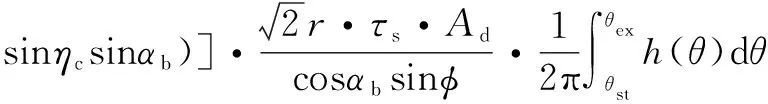
(4)

式中：为刀具半径；为轴向切削深度；为啮合角；为脱离角；为剪应力。

函数()的定义如下：

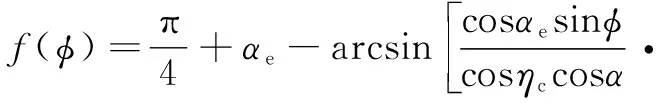
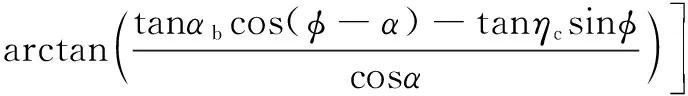
(5)

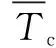
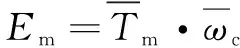
(6)

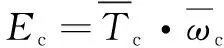
(7)

类似地，有：

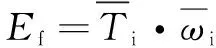
(8)

只要主轴转速指令不变，主轴的运动能量几乎不会波动。因为主轴转速几乎是恒定的，可得出：

=-

(9)

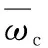
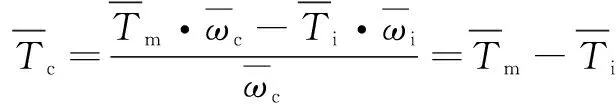
(10)

通过式(4)(10)可以从主轴电机扭矩中识别出剪切角，而不需要进行初步切削实验。

2 实验结果与分析

2.1 实验条件

为验证所提模型的正确性，在4组不同条件下进行切削实验。五轴加工机床型号为NMV 5000 DCG，如图4所示。

图4 五轴加工机床实物

工件材料为A5052铝合金，刀具为直径为12 mm的平头立铣刀，切削刃条数为2，螺旋角为30°。前角和倾角根据刀具几何形状确定,分别为10°和30°。剪切应力由工件材料(A5052铝合金)的剪切屈服应力确定，为145 N/mm。电动千分尺DTH-P20测得的旋转半径偏差Δ为10.8 μm。实验条件如表3所示。

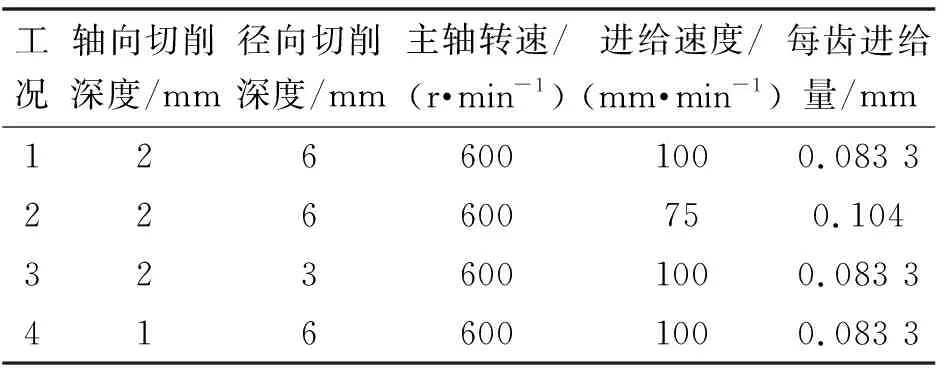
表3 实验条件

2.2 参数识别

在工况1的条件下，确定剪切角和旋转半径偏差Δ。工况1下的主轴电机扭矩如图5所示。

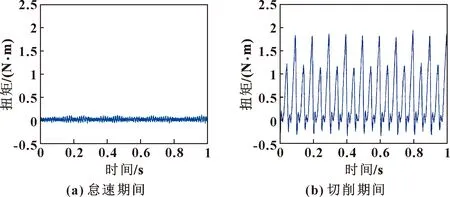
图5 工况1下的主轴电机扭矩

由图5可知：怠速和切削时的平均电机扭矩分别为0.022 6、 0.457 N·m。因此，平均切削扭矩为0.436 N·m。根据图6所示的平均切削扭矩与剪切角之间的关系，可确定剪切角为7.3°。

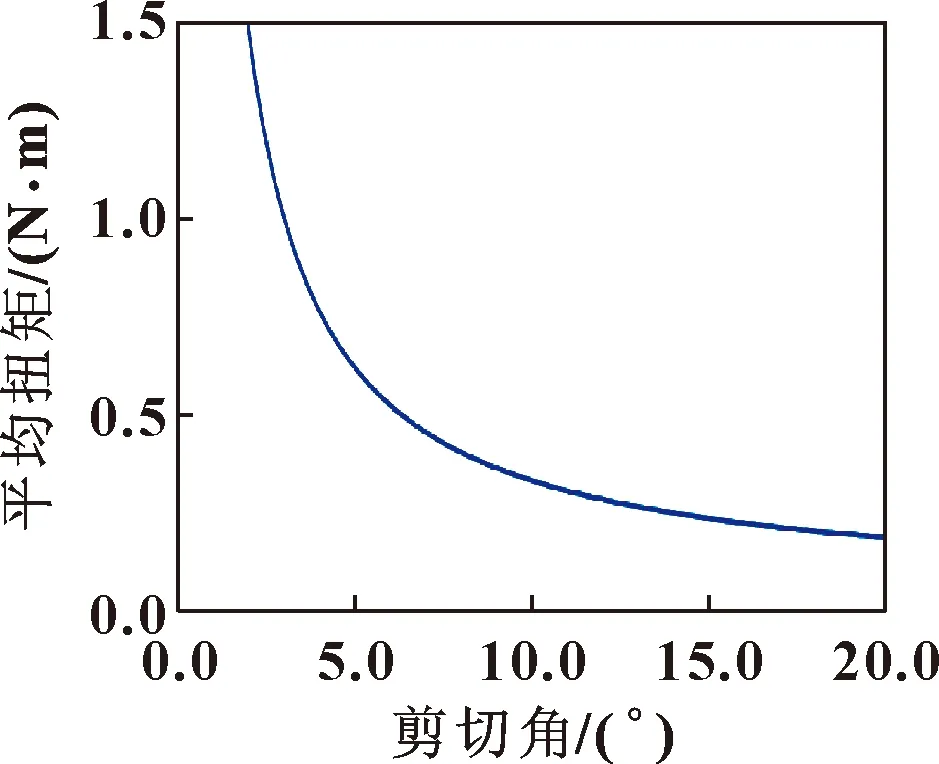
图6 平均切削扭矩与剪切角的关系

图6所示关系曲线是通过迭代计算确定的，无需任何传感器测量即可确定切削力预测所需的参数。

2.3 切削力预测

为验证所提模型的有效性，在表3中列出的4组切削条件下，切削力实测值与预测值的比较如图7所示。可知：切削力在、、轴的分量、和的预测值均与实测值吻合良好，表明使用该模型可以在没有任何前期实验和任何附加传感器的情况下，以较高的精度预测切削力。需要注意的是，由于摩擦角的差异，分量预测值略大于实测值。摩擦角的取值取决于最大剪应力理论的准确性。

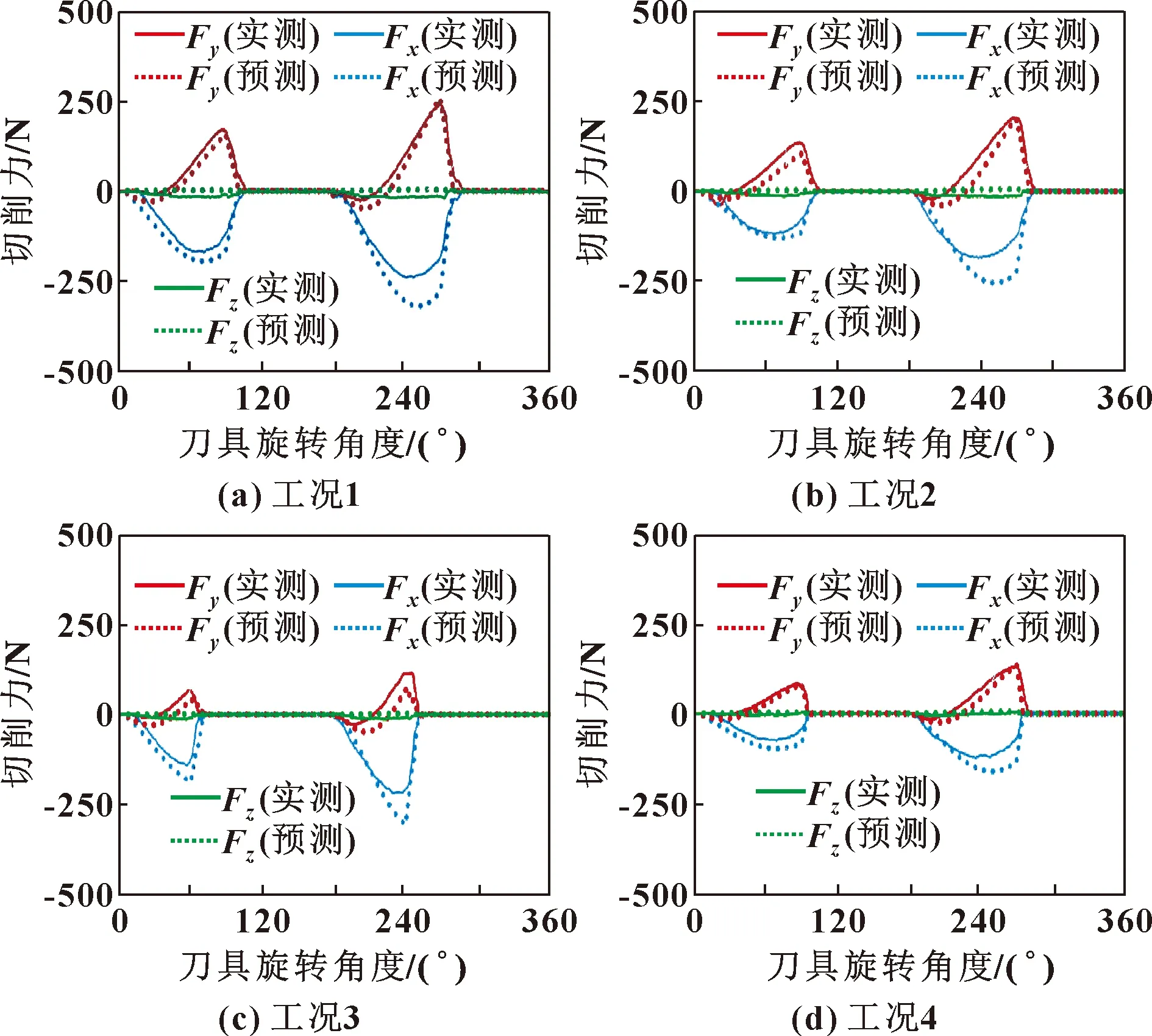
图7 切削力实测值与预测值的比较

3 结束语

本文作者基于斜切削理论和正交切削理论，提出了一种新的切削力预测模型，验证了该模型的可行性。主要结论如下：(1)在该预测模型中，预测切削力只需要剪切角；(2)所需参数可以根据主轴电机扭矩确定，无需额外的传感器监测；(3)即使切削条件发生变化，预测的切削力与测量的切削力也具有较好的一致性。