基于LSSVM的磨加工主动量仪圆度误差在线评定方法研究

张志永，郑鹏，刘栋梁

(1.郑州科技学院机械工程学院，河南郑州 450064；2.郑州大学机械与动力工程学院，河南郑州 450001)

0 前言

磨加工主动测量控制仪(简称主动量仪)是一种在线测量零件加工参数并能控制磨削进程的设备，主要应用于自动、半自动磨床。主动量仪主要由测量装置、驱动装置、控制单元、CNC控制系统、砂轮进给机构等组成，如图1所示。传感测头以接触式相对测量方式将工件尺寸数据实时传输给计量装置。控制单元接收计量装置发送的数据并通过内置算法进行误差评定。当误差超出允许范围边界时，向CNC控制系统发出补调指令。控制系统接收到指令后，通过更改工艺参数对误差进行补调。砂轮进给机构和驱动装置根据指令调整，实现工件尺寸闭环控制。

图1 磨加工主动量仪在线测量原理

现有磨加工主动量仪主要用于测量和控制磨削加工过程中工件的尺寸精度，而圆度误差评定是轴类零件加工检验必不可少的部分。随着现代工业对产品几何要求的不断提高，对圆度误差评定的精度和效率都有更高的要求，需要主动量仪在监测工件尺寸精度的同时能够高效准确地完成工件圆度误差的评定工作，以便省去加工后的检验工序，不仅能够提高工件的加工效率，而且能够降低生产成本。根据GPS和ISO标准可知，根据评定基圆的不同，只有最小区域法的评定准则符合圆度误差定义，适用于高精度的误差评定。但因该方法计算复杂，运算时间长，应用于在线检测方面有一定局限性。

目前已有研究人员在最小区域圆度误差评定的优化算法方面取得了成效。张汛等人提出基于遗传算法(Genetic Algorithm,GA)的圆度误差评定方法，结果表明该算法能比传统优化算法收敛到更精确的解,并具有较高的稳定性,能有效克服局部收敛的问题。申翠香、张晓宇采用量子遗传算法进行多进制编码,提高了圆度测量精度。蒋文兵等利用求解线性规划的单纯形算法(Simplex Algorithm,SA)求得符合最小条件的圆度误差值。罗钧等人提出一种改进的蜂群算法并应用于圆度误差最小区域评定中，能很好地满足新型测量设备对应用软件的要求。蔡朕等人为提高圆度误差评定的准确性和收敛速度,提出了一种改进布谷鸟搜索算法。已有的这些智能优化算法在最小区域圆度误差评定方面有一定的突破，但这些算法求解步骤普遍相对繁琐，有的容易导致局部最优解，有的需要设置参数过多，导致算法收敛速度降低，计算时间变长。支持向量机(Support Vector Machine,SVM)是VAPNIK依据统计学习理论提出的一种机器学习方法，在学习过程中需要求解带约束的二次规划问题，且约束个数等于样本容量，求解过程存在大量的矩阵运算，随着样本数量的增多，计算的复杂度增加，求解时间也随之增加，导致该模型进行圆度在线评定时实时性降低。为了提高其运算速度，SUYKEND等利用具有等式约束并满足KKT条件的规则化最小二乘支持向量机函数作为损失函数，提出了最小二乘支持向量机(Least Squares Support Vector Machines,LSSVM)模型，它具有良好的泛化性能、高计算效率和高维鲁棒性的优点。为了确保在圆度误差评定准确性的前提下提高评定效率，本文作者将具有快速学习能力且鲁棒性好的LSSVM和适用于高精度误差评定的最小区域法相结合，提出了基于LSSVM的圆度误差最小区域评定方法。

1 基于LSSVM的圆度误差最小区域评定模型构建

基于LSSVM的圆度误差最小区域评定模型的思想是将圆度上的采样点映射到高维空间中，求取最优回归函数，再根据回归函数确定圆度评定模型的圆心，最后确定圆度误差。

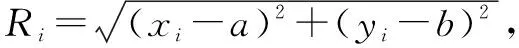
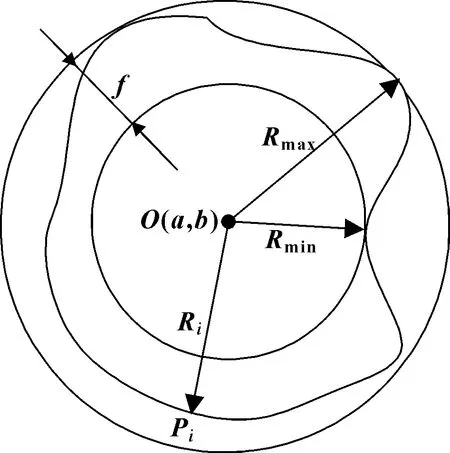
图2 最小区域法圆度误差评定示意

SVM分类的目标函数如式(1)所示：

s.t.(+)≥1=1,2,…,

(1)

SVM回归的公式见式(2)

s.t.|-(+)|≤=1,2,…,

(2)

式中：为不敏感参数。

因此回归支持向量机的问题可以转化为

(3)

其中:为损失函数，表达式如式(4)所示:

(4)

引入松弛因子，将目标式子改写为

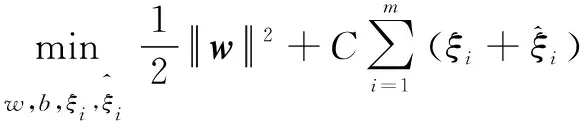
(5)

引入拉格朗日乘子，拉格朗日函数如式(6)所示:

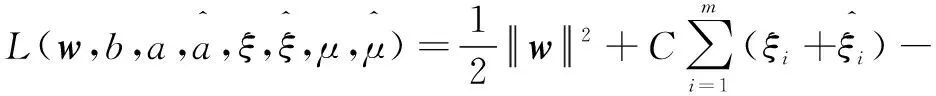
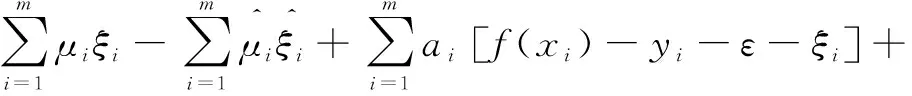
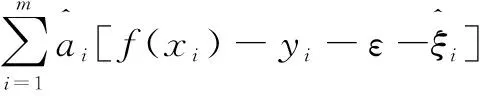
(6)

而LSSVM利用()=·()+进行估计，式中(·)将输入从低维非线性映射为高维线性，把非线性问题转化为高维特征空间中的线性拟和问题。LSSVM的优化问题为

(7)

相比于SVM算法，其约束条件有所不同，变为如下形式：

[·()+]=1-=1,2,…,

(8)

即将SVM的不等式约束改为等式约束，构造拉格朗日函数进行求解：

()+]-1+}

(9)

其中:为拉格朗日乘子。根据KKT条件，得到如下等式约束条件：

(10)

对于=1,2,…,，通过式(10)消去和得到如下线性系统：

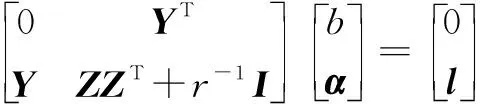
(11)

式中:

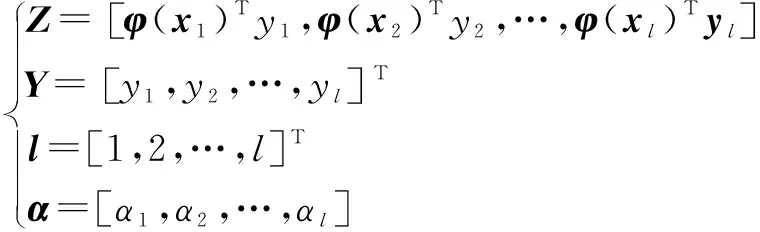
(12)

令=+，求解式(12)得到:

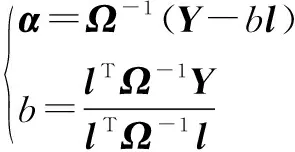
(13)

式(14)为经过解算，推导出的LSSVM最优超平面公式，使用该式可拟合采集到的数据。

(14)

2 基于LSSVM算法评定圆度误差的实现

基于LSSVM算法评定圆度误差的流程如图3所示。

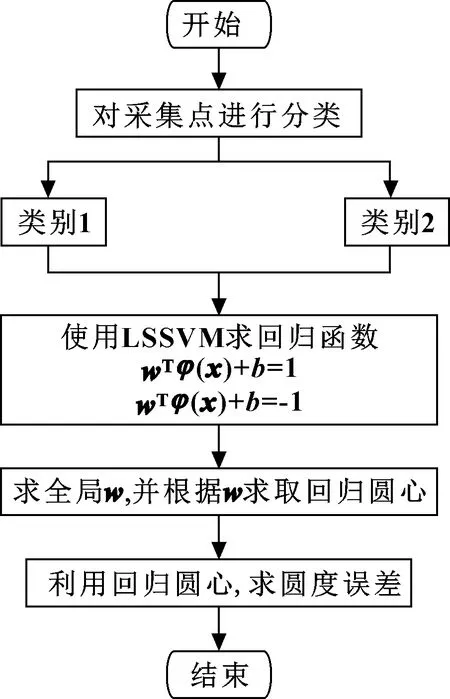
图3 LSSVM圆度误差评定流程

具体步骤如下：

()=·()+

(15)

图4 LSSVM圆度误差评定示意

(16)

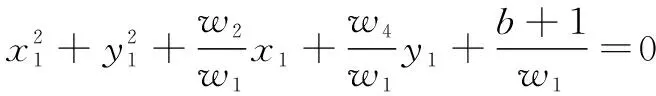
(17)

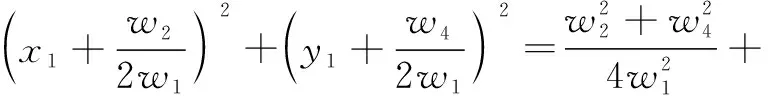
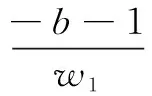
(18)

同理将外圆上的点(,)代入，可得方程(19)—(21)。

(19)

(20)

(21)

使用以上公式，可推导出公式(22)来确定两个同心圆的圆心：

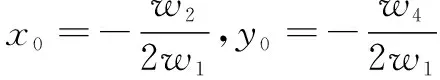
(22)

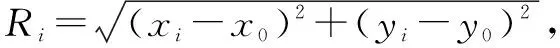
3 实验分析

磨削加工时，需要根据工艺规程设置尺寸特征点。加工进程被特征点分为：快速进给阶段(SZ0)-粗磨加工阶段(SZ1)-半精磨加工阶段(SZ2)-精磨加工阶段(SZ3)-光磨阶段(SZ4)，如图5所示。计量装置由快速进给结束特征点(FP1)开始测量，之后机床执行粗磨加工。当计量装置检测到工件满足第二特征点(FP2)精度要求时，加工进程转换为半精磨状态。当检测到精度满足第三特征点(FP3)时，加工进程变为精磨状态。当工件满足第四特征点(FP4)时，加工进程变为光磨阶段，直至工件满足设计要求(切断点)，砂轮执行回程运动直至下一循环。

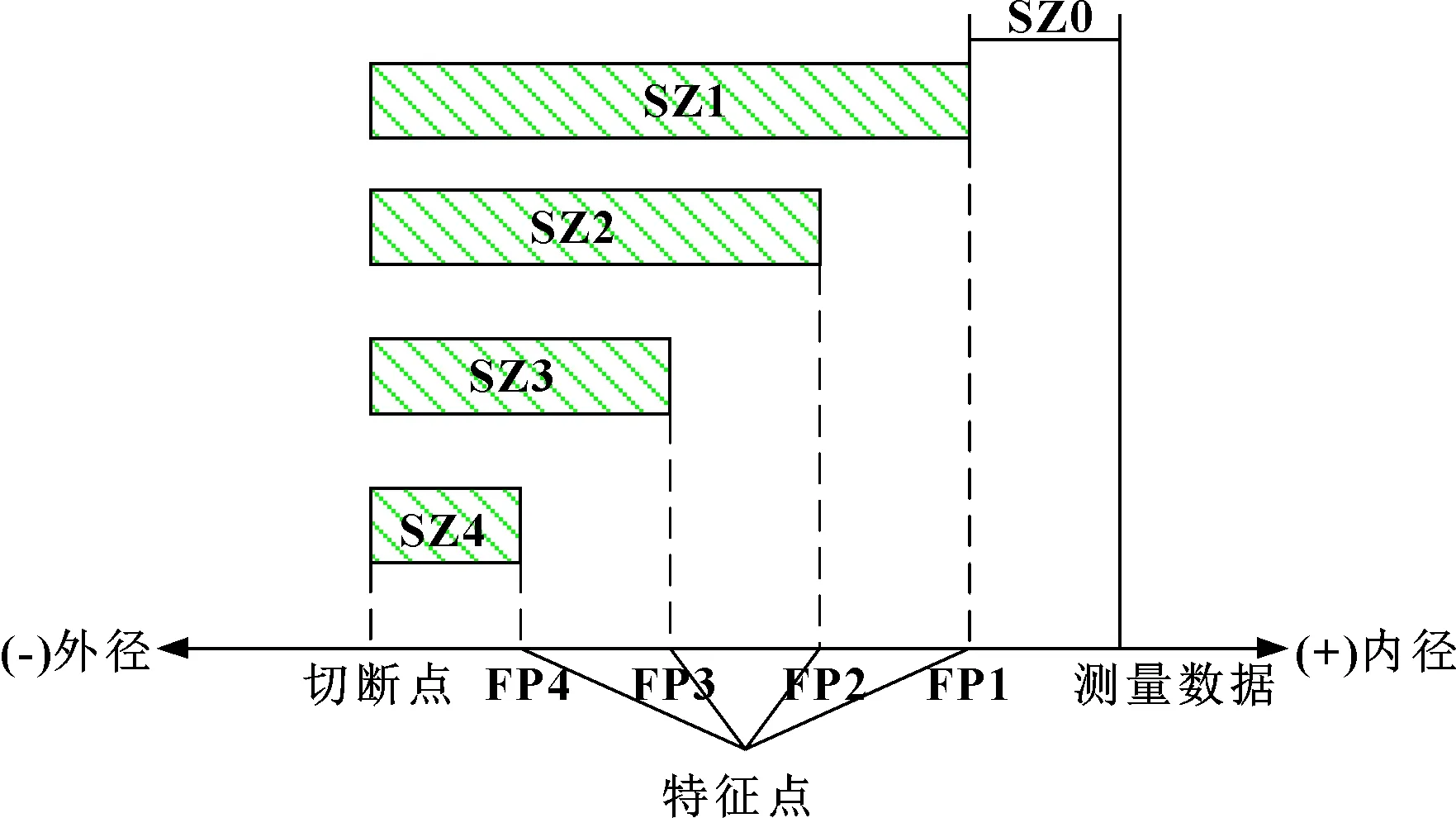
图5 砂轮磨削进程

对磨削加工时工件实际表面轮廓横截面分析可知，在理想条件下工件的表面轮廓截面为阿基米德螺线。而光磨阶段是用以修整和降低工件的圆度误差，可消除砂轮进给所造成的尺寸变化，将工件轮廓截面的“阿基米德螺线”修整为圆。为方便分析和验证基于LSSVM算法进行在线圆度评定时的准确性，实验时选用光磨阶段为研究对象。实验平台为MGB1320E高精度半自动外圆磨床，磨床配备主动测量装置，包括电感式测头及液压驱动装置，经过A/D转换测头数据传输给上位机，如图6所示。砂轮材质为棕刚玉，直径400 mm，厚度32 mm，最高线速度35 m/s；采用GYSyn256C磨削液；磨削方式为外圆径向切入磨削。

图6 实验平台

为了证明基于LSSVM的圆度误差评定方法的准确性和稳定性，分别对某一轴类工件的两个不同轴截面进行测试，每个截面测得10组数据，每组数据采集3 600个点。分别采用GA、SA、SVM、LSSVM 4种算法对每组数据进行误差评定，评定结果如表1、表2所示。可知，采用LSSVM所得圆度误差值精度优于其他3种对比算法所得评定结果，证明了LSSVM算法评定的准确性。且根据图7、图8可知在同一截面进行重复性测试时，该方法也具有一定的稳定性，证明其重复性良好。

表1 截面1圆度误差 单位:μm

表2 截面2圆度误差 单位:μm

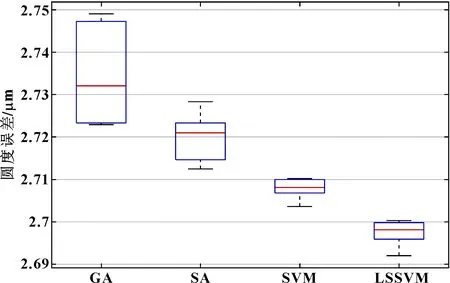
图7 截面1重复测试boxplot图

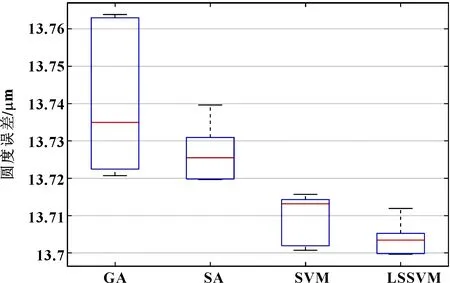
图8 截面2重复测试boxplot图

为了直观验证基于LSSVM评定方法的准确性，对GA、SA、SVM、LSSVM 4种算法评定结果进行仿真，数据来源为截面1的第一组测量数据，仿真结果如表3所示。可知:4种算法所求得的包容圆圆心坐标(,)、被测轮廓最小内切圆半径、被测轮廓最大外接圆半径的值均非常接近。根据表中数据绘制了圆度误差评定模型仿真图，如图9所示。可直观看出:4种算法得出的圆度误差评定的实际圆轮廓高度吻合，可直观证明LSSVM进行圆度误差评定结果的准确性。

表3 截面1评定参数 单位:μm

图9 截面1评定模型仿真

为了进一步验证基于LSSVM的评定方法的准确性，通过实验得出不同方法的计算时间，证明所提方法的高效性。对同一截面测量不同点数，由表4可知:在不同测量点数下GA、SA、SVM和LSSVM所得的圆度误差值一致性良好，且LSSVM评定精度最高，进一步验证了基于LSSVM的圆度误差评定方法的准确性。为了证明该算法的高效性，在同一台计算机上运行以上4种算法得出运算时间，由表5可知:相较于其他3种算法，随着采集点数的增加，基于LSSVM的圆度误差评定方法的评定效率优势愈发凸显，其评定时间受采集点数增加的影响很小，在采集数据量较大的情况下评定效率有显著的优势。

表4 不同采集点数的圆度误差 单位:μm

表5 算法评定效率比对 单位：s

4 结论

采用LSSVM所得圆度误差评定精度优于其他3种对比算法，相比基于GA、SA和SVM算法的圆度误差评定方法，采用LSSVM进行圆度误差最小区域求解可以在保证评定结果准确的基础上，有效提高圆度误差的评定效率，尤其在采集数据量较大的情况下评定效率有显著的优势。经分组重复实验可知，基于LSSVM的算法评定结果稳定，可应用于工业加工中复杂环境下的圆度误差在线评定，从而提高生产效率。该研究对于实现磨加工主动量仪圆度误差的在线评定具有重要意义。基于LSSVM的算法原理简单明了，简化了圆度评定中的算法编程工作，并可推广应用到直线度、平面度、圆柱度等其他形位误差的评定。