一道2021年高考试题的探究与反思

重庆市合川中学 黄富国 王安国 唐义恒 401520

1 试题呈现

试题：（2021 年新高考Ⅰ卷第19 题）记△ABC内角A，B，C的对边分别为a，b，c.已知b2=ac，点D在边AC上，BDsin ∠ABC=asinC.（1）证明：BD=b；（2）若AD=2DC，求cos ∠ABC.

本题为平面几何与三角的综合，主要考察使用正、余弦定理求三角的边长和内角的余弦等内容；能力层面突出考查学生的数形结合能力、推理论证能力、辩证思维能力以及综合运用所学知识分析问题和解决问题的能力，侧重考查逻辑推理、数学运算和直观想象等素养.试题分两问，梯度明显，既能让绝大数考生有所收获，又能区分不同层次的学生.试题常规，但内涵丰富，解法多样，极具探究价值，是一道值得研究的好题.试题（1）由题设，BD=，由正弦定理知，又b2=ac，∴BD=b，得证.下面着重探讨第（2）问.

2 解法探究

评注：试题为有一个公共边的两个三角形结构模型，BD为公共边，∠ADB,∠CDB互补，分别在两个三角形中使用余弦定理，成功地将两个三角形的边、角衔接起来，从而得到试题的解答.这种解法常规，也是学生最容易想到，但要注意多解的取舍、漏解、错解等现象.

评注：有一个公共边的两个三角形结构模型也可以用向量表示，把表示，借助向量的数量积运算，得到三角形边角等式，使用余弦定理，进而得到答案.从解答过程来看，向量法与解法一的三余弦法本质上是一致的.实际上，对于余弦定理的证明教材上也是采用向量法.

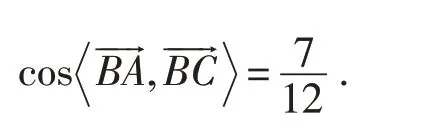
评注：考虑到向量用坐标表示，在△ABC中，先确定点A、C坐标，再探究满足条件点B的运动轨迹.自然会想到，通过建系、设点，求点B的轨迹方程，得点B在圆上运动，再把条件b2=ac坐标化，得到关于点B方程组，解得点B的坐标，利用向量夹角公式求解.相比于解法一、二，解析法不但能减少运算，还形象直观展示满足条件的三角形，避免了三角形多解的讨论.

解法四（平面几何法）:由条件b2=ac，从数列角度来看，a,b,c成等比数列，且b为等比中项，则有a＞b＞c或c＞b＞a，所以∠ABC为锐角.下面分别讨论a＞b＞c或c＞b＞a时三角形△ABC的图形.

当a＞b＞c时，BD=b，∠ABC为锐角，满足条件的三角形△ABC如图2所示.由于，所以sin ∠ABC=sin ∠BDC,又∠BDC为钝角，故∠ABC=∠ADB.在△ABC和△ABD中，∠A=∠A，∠ABC=∠ADB,所以△ABC～△ABD.时，，所以cos ∠ABC=.当c＞b＞a时，BD=b，∠ABC为锐角，满足条件的三角形△ABC如图3 所示.同理，△ABC～△BCD,，不合题意.综上，cos ∠ABC=.

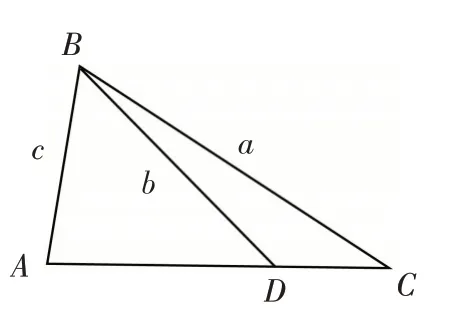
图2

图3

3 试题拓展

从上面的解法中，自然会联想到，如果点D在AC边上移动时，cos ∠ABC的取值如何变化；当点D移动到什么位置时只有一解，什么位置时又存在两解.受到解法四的启发，下面我们尝试从平面几何的角度对试题进行拓展.

拓展2：记△ABC内角A，B，C的对边分别为a，b，c.已知b2=ac，点D在边CA上或AC的延长线上，BD=b.若AD=λCD(λ＞0)，求cos ∠ABC.

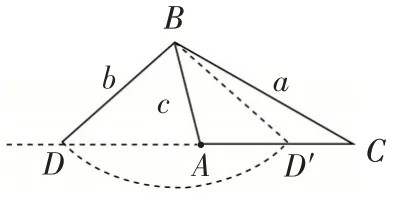
图4

图5

4 反思与小结

4.1 回归教材，立足通性通法

考题的模型来源于课本例题和习题模型，有一条公共边的两个三角形.这条公共边可以是三角形的中线、角平分线或任意一条边.在人教B版教材必修5中，这一模型的试题出现多次，如教材P5 例2，教材P10 习题1-1B：4，教材P20自测与评估第2题、第5题，这些题的公共边为角平分线或中线；又如在教材1.2 应用举例问题2 中，测量地面上两个不能到达的地方之间的距离——两海岛之间的距离.衔接两个斜三角形的公共边就是任意的一条边.此类问题求解的基本思路都是利用公共边和两角互补，去衔接两个三角形，从而达到解决问题的目的.由此可见，高考要考查的考点与教材所要传达的知识点是一脉相承的，课本上着重要传达的思想、解决问题的方法及对应的知识点就是高考中的考点.因此，教师在教学中做到回归基础，从教材中最基本的解决问题的方法入手，总结出同类问题的通性通法.

4.2 重视知识间的联系

“课标（2017 年版）”指出：教学中注意沟通各内容之间的联系，通过类比、联想、知识的迁移和应用等方式，进一步理解数学的本质，提高解决问题的能力.

就本题而言，关键是对“有一个公共边的两个三角形”结构认识，利用两角互补衔接两个三角形得到解法1；联想到这一结构可以用向量表示就有了解法2；考虑到满足条件的三角线的形状，进而探究点的轨迹也就有了解法3；想到b2=ac可以看成等比数列，也可以看成两个三角形中对应边成比例，于是就有了解法4.可见，每一种解法的背后都是知识与方法的交融.以上的四种方法沟通了代数、几何、向量、解析几何的联系，通过对问题的求解，让学生感受代数法、向量法、解析法、平面几何的应用，体会到分类讨论、数形结合、转化与化归等数学思想方法，深化了学生对知识、思想、方法的理解.我们在教学的过程中要帮助学生建构知识的内在联系，完善认知结构.在不断学习的过程中理解数学、感悟数学，激发学生学习数学的灵感，提升学生的能力，培养学生的数学素养.

4.3 重视平面几何知识在解三角中的应用

三角形是最基本的几何图形，解三角形主要是利用正余弦定理研究三角形边长、角度、面积和周长等，本质还是几何问题.初中通过平面几何的性质研究几何图形，如特殊的三角形、勾股定理、三角形相似与全等；高中强调用代数的方法研究几何问题，所以在高中几何学习中学生容易忽视图形的几何性质.一些学生存在一个误区，认为高中的知识“高级”，对初中学过的平面几何知识不屑一顾，不重视平面几何知识在解三角形的应用.高考通常以解三角形、解析几何试题为载体来考察平面几何知识.从解法4可以看到，利用图形几何性质,借助平面几何的知识，不但能避开繁琐的代数运算,使解决问题的过程得到简化,而且能更好地揭示问题的本质.

总之，解三角形在高中数学中占有重要的地位，是高考的重点.试题注重考察基础性和综合性.在高中复习中，要回归教材，注重通性通法，对试题进行一题多解，挖掘知识间的联系，尝试对试题进行拓展，培养学生发散思维和创新意识，感受数学和谐与统一之美.