充分挖掘教材例题的价值——一道圆锥曲线例题引发的思考

河北省邯郸市第一中学 王政敏 056001

在例题教学过程中，教师不能仅局限于分析例题特点，教会例题解法，而应该充分挖掘例题的教学价值.在2021 年人教版高中新教材网络培训会上章建跃老师提到：在圆锥曲线一章教科书中的例题与习题，其选编的原则是帮助学生深入理解圆锥曲线的几何特征，熟练运用坐标法研究圆锥曲线的性质以及它们的位置关系，并能解决一定综合性的问题，通过解题感悟解析几何中蕴含的数学思想.具体的题目是研究圆锥曲线的性质，应注意这些题目的教学功能，使学生认识到认真解答这些题目的重要性，必要时可以对有关题目进行适当的变式拓展.在教学中引导学生思考例题的结论能否抽象得到一般性的命题，在对问题探究得出结论、应用结论的过程中，有效发展学生数学抽象、逻辑推理和数学运算等核心素养.

1 教材例题

例1 设A,B两点的坐标分别为(-5,0),(5,0)，直线AM,BM相交于点M，且他们的斜率之积是-，求点M的轨迹方程.（人教A版高中《数学》选择性必修一，P108）

分析：如图1，设点M的坐标为(x,y)，那么直线AM,BM的斜率就可以用含x,y的关系式分别表示.由直线AM,BM的斜率之积是，可得出x,y之间的关系式，进而得到点M的轨迹方程.

图1

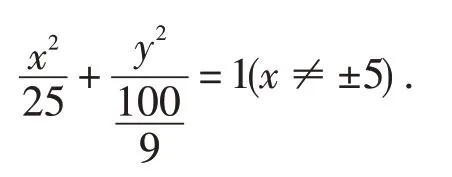
2 抽象结论

3 灵活应用

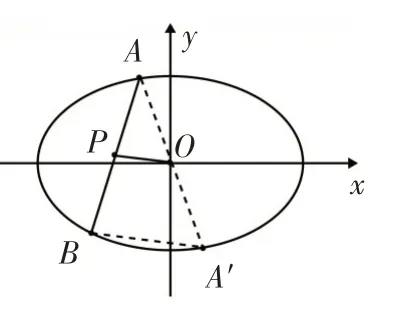
图2

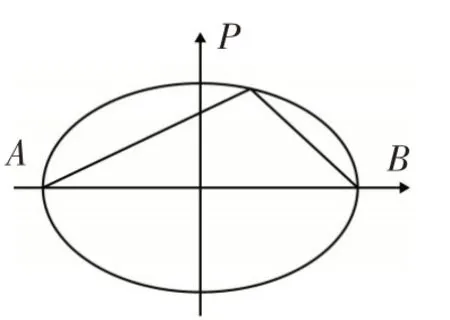
图3

解题反思：注意到这个题目中有对称的两点，借助上面定理找到解题入口.

例4（2019 年全国卷II 第21 题）已知点A(-2,0)，B(2,0)，动点M(x,y)满足直线AM与BM的斜率之积为-.记M的轨迹为曲线C.(Ⅰ)求C的方程，并说明C是什么曲线；（II）过坐标原点的直线交C于P，Q两点，点P在第一象限，PE⊥x轴，垂足为E，连结QE并延长交C于点G.（i）证明：△PQG是直角三角形；（ii）求△PQG面积的最大值.

解析：本题是高考压轴题，总共3 问，第（I）问求轨迹及轨迹方程，同课本例题，第（II）(i)是三角形形状的判断与证明，第（II）（ii）是求三角形面积最值.

（I）考察了求轨迹方程的基本方法与步骤：（1）设动点坐标为(x,y) ；（2）根据条件建立等式关系；（3）代入坐标运算；（4）化简整理；（5）检验.这里动点M(x,y)已给出，结合题目中“AM与BM的斜率之积为-”，即有kMA·kMB=-，代入坐标得kMA·kMB=，化简整理得.这问虽然简单但易错，在求轨迹方程时一定要注意检验，条件中提到“AM与BM的斜率”，即两直线的斜率是存在的，故x≠±2，所求的轨迹方程为（x≠±2），轨迹是椭圆，不含左右两个顶点.

（II）分为两小问，均是在△PQG下进行的设问，需要把握图形的构建过程，基于几何与函数的坐标联系来解析.

解题反思：这个经典高考题的前两问都来源于课本例题，在日常教学中要充分挖掘课本题，重视课本例题和习题的练习.

圆锥曲线丰富多彩的性质常作为例题和习题，不仅使题目的思想内涵得到增强，而且通过这些题目加强了知识间的相互联系，从而帮助学生建立对圆锥曲线的整体认识.例如椭圆的例题中，就包含了椭圆与圆的联系、定义椭圆的其他方式、椭圆的光学性质等，这些题目的“数学含金量”是非常高的，而且这些题目的可拓展性也很强，在教学中要充分挖掘.