“对分课堂”在“两角差的余弦公式”教学中的运用

浙江师范大学物理与电子信息工程学院 孔胜涛 321004

“对分课堂”是复旦大学张学新教授于2014 年首先提出来的一种有机融合讲授式教学与讨论式教学优点的教学模式，其具体操作流程如下：教师讲授（Presentation）→内化吸收（Assimilation）→讨论（Discussion），简称为PAD 课堂，又称为对分课堂[1].近几年，笔者在数学课堂教学中，多次尝试运用“对分课堂”教学模式，取得了较好的教学效果.

下面以人教A《数学》必修4 中“两角差的余弦公式”的一个教学片断为例，介绍在数学课堂教学中尝试运用“对分课堂”教学模式的一些做法和思考，与大家商榷.

1 教学片断

1.1 教师讲授(Presentation)

问题1 如图1 和图2，在平面直角坐标系xOy内作单位圆O，以Ox为始边作角α，β，他们的终边与单位圆O的交点分别为A，B.则如何用角α，β的正弦、余弦值来表示cos(α-β)呢？

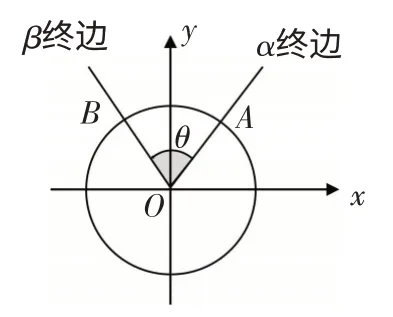
图2

设计意图：通过对此问题的解析，引领学生回顾平面向量数量积的定义，平面向量数量积的坐标运算，余弦函数的诱导公式等基础知识，从中体会向量方法在推导两角差余弦公式中的应用.（在此教学环节中，教师的讲解要精练，学生要记听课笔记）

公式①给出了任意角α，β的正弦、余弦值与差角α-β的余弦值之间的关系.称为两角差的余弦公式.

1.2 内化吸收(Assimilation)

这是“对分课堂”教学模式的第二个环节，也是非常重要的一个环节，教师若重视这一环节，不仅有利于提升学生学习的主动性和积极性，而且有利于培养学生的问题意识.在此环节中，教师可引导学生通过“亮考帮”对上述的讲授内容进行内化吸收.

“亮”即“亮闪闪”，请学生说出经教师讲授及自主学习后自己收获最大、感受最深的一点，用一句话概括.例如，在这节课上，通过“亮闪闪”生1 说出“从上述的解析1 中不难看出，在推导两角差的余弦公式时，注重运用向量方法不仅可使推导过程化繁为简，而且可使推导过程化难为易”.

“考”即“考考你”，请学生把自己弄明白的知识点以问题的形式提出来，小组讨论时考考其他成员.例如在这节课上，通过“考考你”生2提出“在上述的解析1中，公式①是在α，β∈[2kπ,2kπ+π]，k∈Z 的情况下得到的，那么你能证明公式①在α，β∈(2kπ+π,2kπ+2π]，k∈Z 的情况下仍然成立吗？”

“帮”即“帮帮我”，请学生把自己不明白的知识点以问题的形式提出来，小组讨论时求助别人.例如在这节课上，通过“帮帮我”生3 提出“从上述的解析1 中发现，当α-β=2kπ±θ时，公式①成立，但在图3和图4 的情况下，α-β≠2kπ±θ，此时公式①是否也成立？”.

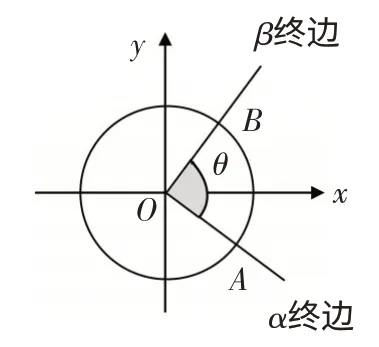
图3

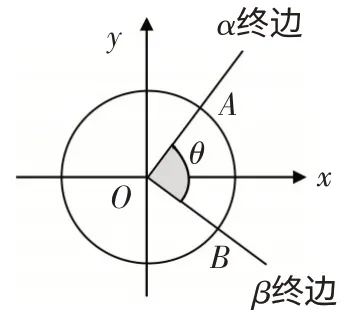
图4

1.3 讨论（Discussion）

这是“对分课堂”教学模式的最后环节，在此环节中，教师可先让学生分组围绕“内化吸收”环节所提出的问题进行讨论，然后再对各小组讨论所产生的困难或疑问进行适当的引导.

师：谁能回答生2所提出的问题吗？

教师的话音刚落，有一位男生举手.

生4（组1）：老师，我们小组能证明公式①在α，β∈(2kπ+π,2kπ+2π]，k∈Z 的情况下仍然成立.

师：很好！请你代表组1 到讲台上给大家讲解一下.

师：很好！组1 的证明方法不仅过程简洁，而且思路清晰.让我们再次为组1的简洁证法鼓掌（组1欣喜）！

生3：老师，我们小组到现在还没有解决我所提出的问题，您能讲解一下吗？

师：生3 的问题是从上述的解析1 中发现，当α-β=2kπ±θ时，公式①成立，但在图3和图4的情况下，α-β≠2kπ±θ，此时，公式①是否也成立？其他小组有同学能回答生3所提出的问题吗？

巡视课堂后，教师发现学生仍没有找到思路.因此，教师继续向学生追问：在上述的解析1 中，夹角θ的取值范围是什么？在图3 的情况下，当时，α-β与θ之间有什么关系？在图4 的情况下，当时，α-β与θ之间又有什么关系？

在教师的追问下，学生有了讨论的方向，经过一番分组讨论，师生合作给出了如下的解析.（教师巡视，并请生5 在黑板上板书.）

生5 的板书刚一结束，教室里自发地响起一片掌声.

师：非常好！生5 的解题思路流畅，运算过程正确，板书清晰，字体优美，赞一个.生3，现在你能看懂上述的解析2吗？

生3：老师，我能看懂上述的解析2，我已明白：任意角α-β要么与θ的终边相同（如图1），要么与2π-θ的终边相同（如图3）；任意角β-α要么与θ的终边相同（如图2），要么与2π-θ的终边相同（如图4），这时仍然有 cos(α-β)=cos(β-α)=cos(2π-θ)=cosθ.因此，公式①对于任意角α，β均成立.

师：生3 提的问题很好！刚才的回答也很好！请同学们课后思考上述的解析1 是否需要订正？如有需要，如何订正？

评注：在“对分课堂”上留出足够的时间让学生讨论生2 和生3 所提出的问题，旨在充分发挥学生学习的主动性和积极性，从而让学生进一步体会和理解平面向量数量积的定义，平面向量数量积的坐标运算，余弦函数的诱导公式等基础知识及向量法在推导两角差余弦公式中的应用.

2 教学思考

从上述的教学片断中，我们不难发现，运用“对分课堂”教学模式进行高中数学课堂教学的意义主要在于以下两点：

2.1 有利于提升教学的系统性和高效性

“对分课堂”教学模式的第一个环节是教师讲授，而讲授式教学的主要优点是能充分发挥教师的主导作用，有利于提升知识传授的系统性和高效性.由于教师闻道在先，术业有专攻，能够比较系统、准确地领会教材编写意图，吃透教材、挖掘教材的深邃内涵，所以教师能在单位时间里向学生迅速传授较多的系统的数学知识.如在这节课上，通过教师讲授，教师能在较短的时间内，引导学生运用向量法完成两角差余弦公式证明的教学任务，这就是讲授式教学的优点.因此，“对分课堂”教学模式的优点之一是有利于提升知识传授的系统性和高效性.

2.2 有利于提升学生学习的主动性和积极性

“对分课堂”教学模式的第二个环节是内化吸收、第三个环节是讨论，在教师讲授和讨论之间增加内化吸收环节，这是“对分课堂”教学模式的一大创新点.作为讨论之前的内化吸收，不仅有助于学生主动积极地参与讨论，而且有助于讨论的深入进行.又因讨论式教学的主要优点是能充分发挥学生的主体作用，有利于提升学生学习的主动性和积极性.如在这节课上，学生能主动积极地参与生2 和生3 所提出问题的讨论，学生能在课堂上提出“从上述的证明1 中发现，当α-β=2kπ±θ时，公式①成立，但在图3 和图4 的情况下，α-β≠2kπ±θ，此时，公式①是否也成立？”如此的好问题，让教师都感到十分意外，这问题有利于大幅度提升学生学习的主动性和积极性.因此，“对分课堂”教学模式的优点之二是有利于提升学生学习的主动性和积极性.