初中教师编拟数学试题时的常见失误分析
2022-09-17河北省顺平县教育局教研室郑泉水072250
河北省顺平县教育局教研室 郑泉水 072250
考试是教学中的一个重要环节,通过考试检验了学生的学习效果和教师的教学效果.考试就离不开编拟试题,编拟试题首先要保证其科学性,但不少教师在编拟试题时常常出现瑕疵甚至错误,值得引起大家的警惕!下面就教师在编拟试题时出现的一些问题做一归纳总结,供大家参考借鉴.
1 忽视有图与无图的区别
例1 如图1,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( ).
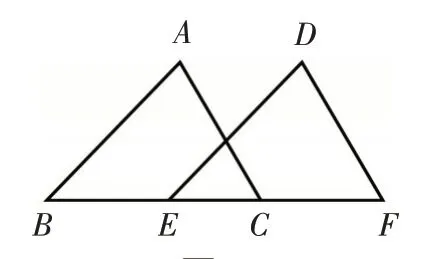
图1
(A)∠A=∠D(B)BC=EF
(C)AC=DF(D)∠ACB=∠F
原题给出的答案是(C).
评析:①本题原意是考查“有两边及一边的对角对应相等的两个三角形不一定全等”,但由于本题中图形已经给定(显然是两个锐角三角形),而由“正弦定理”易知,这样的两个三角形是全等的(其实,有两边及一边的对角对应相等的两个钝角三角形也是全等的)!故此题是错误的!②有些几何题目,如果没有给出图形而需要解题者自己画出图形,此时就要考虑是否有多种情形(分类讨论);而一旦给出图形(只要不是动态的)就无需分类讨论,如例1.再如:已知一个三角形两边的长分别为5 和4,第三边上的高是3,求第三边的长.此题由于没有给出图形,故解答此题需要考虑第三边上的高在三角形内和三角形外两种情形(答案:,而如果此题加上“如图2所示”这样的条件,那么我们还用分类讨论吗?

图2
2 忽视考查方向
例2 下列从左到右的变形是因式分解的是( ).
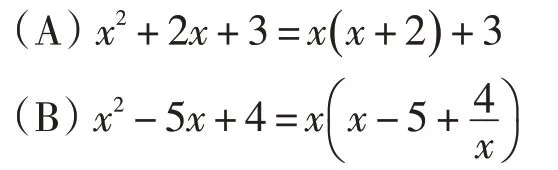
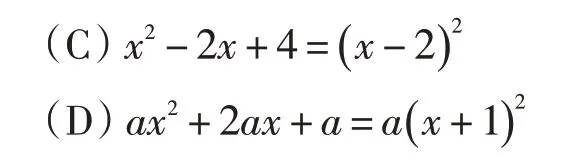
原题给出的答案是(D).
评析:①本题给出的答案虽然没错,但题中的选项(C)却有问题!因为题目考查的是因式分解的概念,而选项(C)考查的却是因式分解是否正确,显然与题目的考查方向不一致,是不可取的!②不少教师认为:只要题目有正确的选项,又不影响学生答题,那么,其它选项就无所谓了.这显然是一种错误的认识!数学是一门严谨的科学,来不得半点马虎,如果教师没有严谨的态度,那我们又如何去教育学生树立严谨的态度呢?
3 忽视某些数学概念的不严谨性
例3 下列式子从左到右的变形属于因式分解的是( ).

原题给出的答案是(B).
评析:按照我们对因式分解的习惯认识,此题似乎没有问题.因为教材中因式分解的定义是“把一个多项式化成几个整式的积的形式叫做这个多项式的因式分解”,据此定义,选项(B)应该属于因式分解.但问题来了:大家都认为多项式3x-1不能再进行因式分解,可如果我们做变形,它就化成了整式3 和整式的积,它和选项(B)的变形不是一样吗?这又怎么解释呢?其实,在代数科学中,“多项式的因式分解”的严格定义应该是“把一个多项式化成几个非平凡因式的积的形式叫做这个多项式的因式分解”.那么,什么是多项式的“非平凡因式”呢?我们先来弄清什么是多项式的“平凡因式”,因为“平凡因式”清楚了,“非平凡因式”就自然清楚了:任何一个非零实数(常数)、多项式本身、以及多项式本身的实数(常数)倍,都叫这个多项式的“平凡因式”.那么,除去“平凡因式”之后,多项式的其它因式就是多项式的“非平凡因式”,如x2-1 的平凡因式有3,x2-1,2x2-2,等等,而x+1,x-1则是x2-1 的非平凡因式.这样一来,我们就清楚了,按照“多项式的因式分解”的严格定义来说,4x+2=2()2x+1 和3x-1=3(x-)都不是因式分解.
4 已知数据错误或自相矛盾

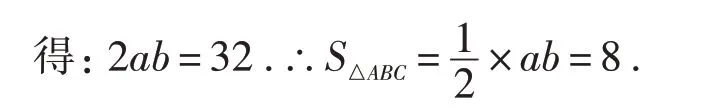
评析:从上述解答看,题目本身似乎没有问题!但仔细分析就会发现Rt△ABC斜边上的中线长是2,则斜边上的高必小于或等于2,故其面积SΔABC≤×4×2=4.可我们求得的面积却是8!问题出在哪里呢?

启示:在编拟试题时,我们不要以为解题过程和解题结果准确无误,所编拟的试题就没有问题,还必须要考虑到已知条件本身是否合理,以确保命制的试题科学无误.
5 小前提与大前提矛盾
例6 如图3,∠AOC和∠BOD都是直角,OB在∠AOC内.解答下列问题:(1)若∠AOB=25°,求∠AOD的度数;(2)若∠AOB=m°,则∠AOD的度数为_____;(3)若∠AOC=∠BOD=m°,∠AOB=n°,求∠AOD的度数.
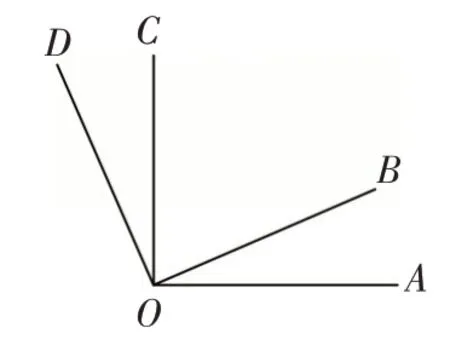
图3
评析:①本题的大前提是“∠AOC和∠BOD都是直角”,而第(3)问中的小前提却是“∠AOC=∠BOD=m°”,它显然与大前提相矛盾;②小前提与大前提相矛盾是一种逻辑错误,在命题时一定要注意这一问题!
6 实际问题不符合实际
例7 阳光中学举办了一次越野赛跑,在这次越野赛中,当小明跑了1600 米时,小刚跑了1480 米,此后两个人分别以a米/秒和b米/秒匀速跑,又过100 秒时小刚追上小明,200 秒时小刚到达终点,300 秒时小明到达终点.问这次越野赛跑的全程是多少米?
原题解法为:由题意得

评析:①从表面上看,此题没有任何问题,可仔细分析你会发现小明赛跑的速度(1.2米/秒)有问题!因为一个人正常走路的速度约为5 公里/小时,约合1.39 米/秒.难道赛跑的速度比走路的速度还慢?②在实际问题的命题过程中,我们不能仅仅考虑问题是否可解,还要考虑其中的数据是否符合实际.
7 已知条件不完整
例8 下列事件是随机事件的有().
(1)小龙玩了一局斗地主;(2)小亮期末考试数学成绩为99 分;(3)小明买了一张体育彩票;(4)小路出国旅游遇见熟人.
(A)1个 (B)2个 (C)3个 (D)4个
原题答案为(D).
评析:“小龙玩了一局斗地主”,“小明买了一张体育彩票”,结果怎么样?题目没有交待清楚,它们都算不上一个完整的事件.完整的叙述方式应该是:“小明买了一张体育彩票就中奖了(或没有中奖)”,“小龙玩了一局斗地主,赢了(或输了).”
例9 八年级(1)班共有学生45 人,其中男生25 人,李老师在该班上课时随意叫起一名同学回答问题,恰好叫到女生的概率是_____.
评析:①我们知道,古典概率的两个要件是随机性、等可能性.上例中,每一名学生被叫到的可能性不一定是相等的,因为教师叫哪一名学生回答问题具有一定的主观性,除非将每一名学生的名字都写在相同的纸条上做成“阄”,然后采用“抓阄”的方式确定哪一名学生回答问题,这样才能保证每一名学生被叫时具有“等可能性”.②在命题时,我们不能凭“习惯上认为”、“想当然怎样”,而必须严格按照数学的要求考虑问题,否则就会犯错误.
总之,编拟试题是一件严谨、细致的事情,它不仅需要全身心的投入,严格照章办事,还需要有所创新.但愿各位同行都能命制出科学性、灵活性、创新性兼备的高质量试题!
