“一题一课”在初中数学教学中的应用

江苏省邳州市明德实验学校 李克民 221399

“一题一课”就是教师深入研究一道习题或者数学材料，透过材料的表面现象，抓出问题所隐含的数学本质内容，进行细致分析，多角度、多维度对问题进行解析，特别是对于一些核心知识要进行发散式讲解，不局限于知识本身，要进行深度拓展，把与知识点相关联的内容都引申出来，使学生的知识面得到拓宽、加深，使学生的知识结构得到完善.本文以“一题一课”的几种教学方式为例，谈它们在初中数学教学中的应用策略.

1 一题多解，让学生的解题思维得到拓展

所谓“一题多解”就是从不同角度、按不同思路、用不同方法给出同一道习题的解答.教师在教学过程中实施一题多解和学生在学习过程中尝试一题多解，不仅能调动学生学习的积极性，而且通过一题多解能使学生达到“思考一道习题，通晓一片知识”，让知识在学生脑袋中形成一条知识链.另外，教师出示题目后，不要过多的给与提示，避免学生的思维被老师过早的给定了方向，应让学生自由思考，让学生原生态的想法得到暴露，思维得到有效的拉伸.

例1 如图1，在△ABC中，点D、E分别是线段BC和AD的中点，连接CE并延长，交AB于点F.求证：

本题主要考查相似三角形的判定与性质，通过在某个拐点处添加平行线，构造“A”型或者“X”型的相似三角形，借助基本图形中对应线段成比例来解决的典型问题.

1.1 构造“ A”型基本图形

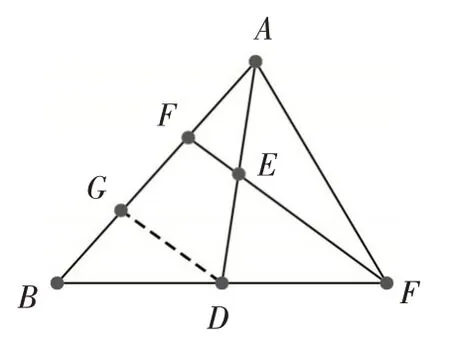
图2

解法2：过点B在三角形外构造“A”型基本图如图3，过点B作BG∥CF交AD延长线于点G,所以∠DCE＝∠DBG，因为点D是BC的中点，所以BD=CD，又因为∠BDG＝∠CDE，所以△BDG≌△CDE，所以DE=DG，因为点E是AD的中点，所以AE=DE，所以AE=DE=DG，所以，在△ABG中EF∥BG，所以△AEF∽△AGB，有

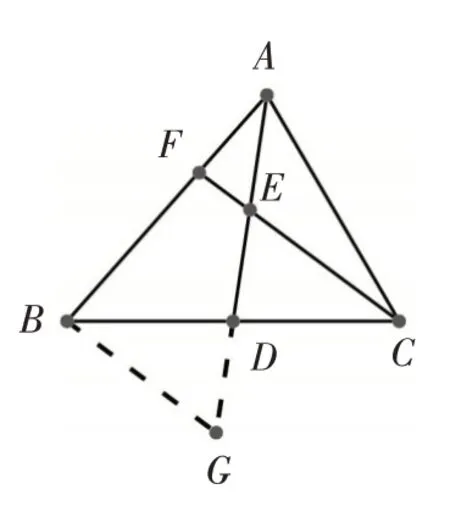
图3

解法3：过点A在三角形外构造“A”型基本图如图4，过点A作AG∥CF交BC的延长线于点G,在△ADG中CE∥AG,所以△DCE∽△DGA,所以,因为点E是AD的中点，所以AE=DE=DA,所以DC=CG=DG,因为点D是BC的中点，所以BD=DC，所以.在△ABG中CF∥AG，所 以△BCF∽△BGA，所以,所以

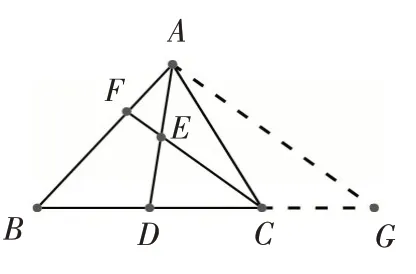
图4

1.2 构造“X”型基本图形

解法4：过点D在三角形内构造“X”型基本图如图5，过点D作DG∥AB交CF于点G.因为DG∥AB，所以∠EAF＝∠EDG，因为点E是AD的中点，所以AE=DE,又因为∠AEF＝∠DEG,所 以△AEF≌△DEG(ASA)，所以AF=DG.因为点D是BC的中点，所以BD=CD,在△BCF中DG∥BF，所以，所以

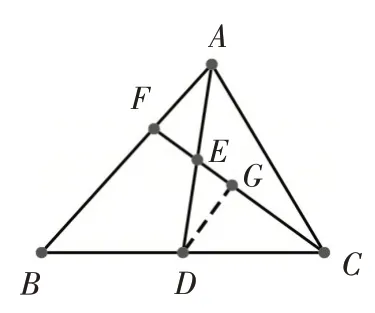
图5

解法5：过点C在三角形外构造“X”型基本图如图6，过点C作CG∥AB交AD的延长线于点G，因为CG∥AB，所以∠ABD＝∠GCD，因为点D是BC的中点，所以BD=CD,又因为∠ADB＝∠GDC，所以△ABD≌△GCD(ASA),所以AB=GC，AD=GD.因为点E是AD的中点，所以AE=DE=，所以GE=3AE，因为CG∥AB，所以△AEF∽△GEC，所以,所以

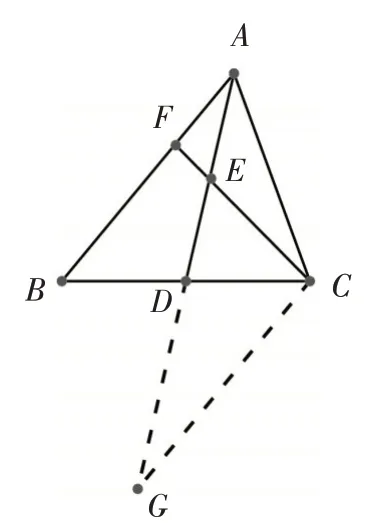
图6

解法6：过点A在三角形外构造“X”型基本图如图7，过点A作AG∥CB交CF的延长线于点G,因为AG∥CB，所以∠AGE＝∠DCE，因为点E是AD的中点，所以AE=DE,又因为∠AEG＝∠DEC，所以△AEG≌△DEC(ASA),所以AG=CD，因为点D是BC的中点，所以，所以，因为AG∥CB,所 以 △AGF∽△BCF，所以,所以

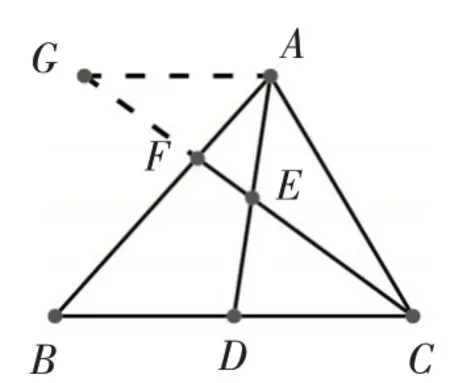
图7

1.3 借助面积求线段的比

解法7：如图8，连接DF，设△AEF的面积为m，△ACE的面积为n，因为点E是AD的中点，所以AE=DE，所以△AEF与△DEF，△AEC与△DEC的面积相等，都是等底等高，所以△DEF的面积是m，△DEC的面积是n,所以△DFC的面积是m+n，因为点D是BC的中点，所以BD=CD所以△BDF与△DFC的面积相等为m+n，所以△ABC的面积是3(m+n)，所以

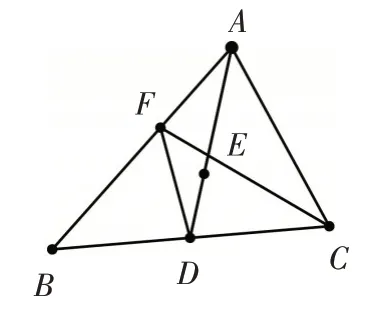
图8

本题是在学生学完相似三角形的性质与判定的基础上进行考查的.学生已具备初步利用相似三角形解决问题的能力，好奇心和表现欲都非常强，让学生根据题目给出的已知条件，结合自身情况，灵活地选择解题切入点，去追求更独特、更快捷的解题方法，要给予学生足够的时间去活跃思路，使学生不满足仅仅得出一道习题的答案，更重要的是积累解题经验，丰富解题方法，学会如何综合运用已有的知识不断提高解题能力，这样有利于锻炼学生思维的灵活性，培养了学生的创新思维.

2 一题多变，让学生的思维能力得到提升

教师在试题评析时，不要单纯地就题论题，而要尽量对试题隐含的知识、思想方法、解题的思路等进行深度的挖掘，拓宽试题的广度，让试题有效的辐射相近知识点.把类似的知识有效的穿成一条知识链，通过一题的解决，让学生通晓一大片的知识.

例2 如图9，已知点C是线段AB上的一点，△ACM、△CBN都是等边三角形.求证：AN=BM.

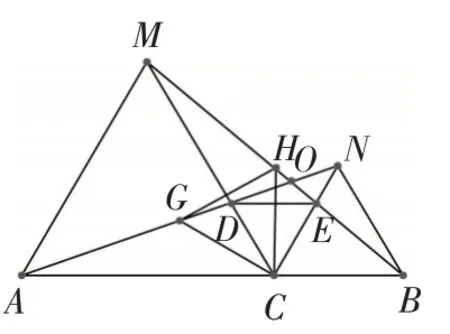
图9

解：因为△ACM、△CBN都是等边三角形，所以AC=MC,NC=BC,∠ACM=∠BCN=60°所以∠MCN=60°，所以∠ACN=120°，∠MCB=120°，所以∠ACN=∠MCB，在△ACN和△MCB中，AC=MC，∠ACN=∠MCB，NC=BC，所以△ACN≌△MCB，所以AN=BM(SAS).

本题主要考查等边三角形的性质，全等三角形的判定和性质，本题证明线段相等，学生不难想到证△CAN≌△MCB，利用三角形全等，对应的边相等，从而证明结论.在评讲本题时，没有局限于结论的证明，而是利用图形，进行一系列的变式探究，强化学生对知识的理解.

2.1 变式：改变结论

例3 如图10，已知点C是线段AB上的一点，△ACM、△CBN都是等边三角形.求证：△ACD≌△MCE.

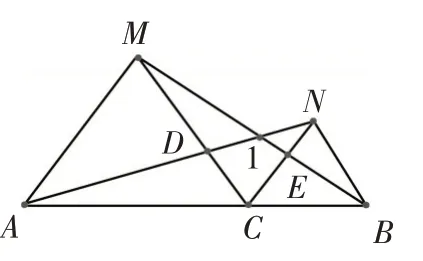
图10

解：因为△ACM、△CBN都是等边三角形，所以AC=MC,NC=BC,∠ACM=∠BCN=60°，所以∠MCN=60°，所以∠ACN=120°，∠MCB=120°，所以∠ACN=∠MCB.在△ACN和△MCB中，AC=MC，∠ACN=∠MCB，NC=BC，所以△ACN≌△MCB，所以∠CAN=∠CMB,在△ACD和△MCE中，∠CAN=∠CMB,CA=CM，∠ACD=∠MCE,所以△ACD≌△MCE(ASA).

2.2 变式：变图拓展

本题还可以在例题2 的基础上，将问题设置为：（1）连结DE，求证△CDE为 等边三角形；或者是证明DE∥AB；（2）连接AN与BM交于点O，求∠MOA的度数.上述问题，对于问题的广度和深度都进行了深度挖掘，通过解决问题训练学生的思维能力，对图形进行变化，可以得到下面的拓展题.

例4 如图11，点C为线段AB上任意一点（不与A、B重合），分别以AC、BC为一腰在AB的同侧作等腰△ACD和等腰△BCE，CA=CD，CB=CE，∠ACD与∠BCE都是锐角且∠ACD=∠BCE，连接AE交CD于点M，连接BD交CE于点N，AE与BD交于点P，连接PC.（1）求证：△ACE≌△DCB;（2）请判断△AMC与△DNP的形状有何关系，并说明理由；（3）求证：∠APC=∠BPC.

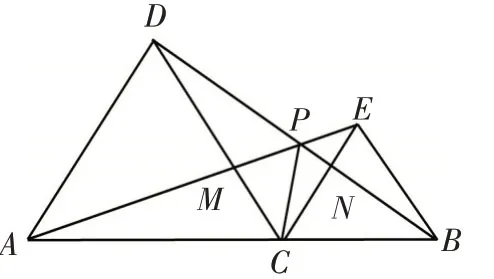
图11

3 几点教学启示

“问题”是建构课堂的“脚手架”，亦是学生学习和教师教学的起始.新课程标准旨在以转变学习方式为突破口，倡导以问题为中心的教学，基于“问题”的教学已经作为一种课堂教学的新模式被广泛应用于教学活动之中.实践证明，研究“问题”设计的有效性对提高课堂教学质量、促进学生发展至关重要.充分整合课程教学资源，对于“一题一课”的课堂教学来说，关注“核心问题”的设计尤为重要.在“核心问题”的设置中要关注以下方面.

3.1 “核心问题”具有适当的思维深度和广度

学生在数学学习中，面对教师提出的富有挑战性的问题，心理会引发强烈的探究欲望.核心问题富有思维含量和思维张力，核心问题的提出让学生有足够的时间和空间，带着探求的兴趣，激活已有的认知经验，或独立探索、或与同伴合作，自由地思考、积极地讨论，从而设计合理的解决路径，找到解决问题突破口.高质量的核心问题，是改进课堂教学的关键，也是学生从被动接受转向主动探索、从学会走向会学的关键因素.

3.2 核心问题具有鲜明的指向性和高度的整合性

对教学内容反复肢解而成的“碎”问，容易让学生把握不准学习的重点和难点，搞不清一堂课的主要学习任务.而中考数学课堂中的核心问题，则是从这节课的数学本质出发，针对这节课的教学重点、难点，高度提炼而成的，它是一节课的核心任务，是贯穿课堂教学的主线，课堂中派生出的其他问题、任务，都与之有着相关的逻辑关系，教师的教、学生的学都围绕它而展开，可以让学生对数学学习目标更明确、更清晰.

3.3 适当分解问题坡度成问题串

核心问题需要给学生留下充分的思考和探索的空间，但有时单一的核心问题可能会使挑战性过大，让学生产生畏难情绪而退缩，特别是对学习基础薄弱的学生来说，高难度的问题不仅不能激发他们的学习兴趣，反而会挫伤他们的学习积极性，产生负面效应.面对不同能力的学生，要体现一定层次的需求差异，根据不同需求将一个核心问题分解细化成若干个子问题，或者分层设计问题，设置一些台阶以便让更多的学生跳一跳能够得着.