浅谈模型迁移，提高解题能力

贵州省安顺市关岭民族高级中学 杨 勇 561300

弹性碰撞在高考中要求中只限于一维，这个知识点的综合应用是高考的重点，也是难点之一.而在处理此类问题时，通常都是用动量守恒公式：以及能量守恒公式：，求出相应的未知量，但是在常规的化简中会带来很多的麻烦.为能够更有效和简便的处理两质点弹性碰撞问题，下面从质心速度的角度来分析和解决此类问题，并对其模型进行相应的迁移，为高效解题提供有力的帮助.

1 问题分析

例题 如图1 所示，光滑水平面上左端有一轻质弹簧，弹簧左端固定，右端与质量为mB物块B相连，B处于静止状态.平面与一光滑曲面平滑连接.现将质量mA、可视为质点的物块A从曲面上距水平面h=0.8m处由静止释放.mB=3mA，物块A与B发生的是弹性正撞.重力加速度g取10m/s2.（1）求物块A与物块B第一次碰撞前瞬间的速度大小；（2）如果物块B每次碰撞后再回到最初静止的位置时都会立即被锁定，而当他们再次碰撞前瞬间锁定被解除，求出物块A第3次碰撞后瞬间的速度大小.

图1

解析一：动量守恒与能量守恒

（2）由于A、B发生弹性碰撞，规定向右为正，由动量守恒：，由能量守恒：，带入数据得：=2m/s.当A再次与B发生弹性碰撞时，再用动量守恒及能量守恒进行计算，发生3 次碰撞后A的速度大小为0.5m/s，这样反复的化简增加了计算量，解题效率并不高.

解析二：质心速度

根据题意由①得A、B组成系统的碰撞前的速度为：vc=1m/s（方向向左），由⑨得，碰撞之后A的速度大小为：=2m/s（方向向右）.当A碰后又返回，在第二次碰撞之前质心速度为：vc=0.5m/s（方向向左），由⑨得，第二次碰撞之后A的速度大小为：=1m/s（方向向右）.同理可以求出A与B发生第三次碰撞之后的速度大小为0.5m/s，方向向右.

评价：在高中阶段，对于一维弹性碰撞的两体问题，通常是按照常规的化简，把②和③联立求解得碰撞之后A、B的速度公式：

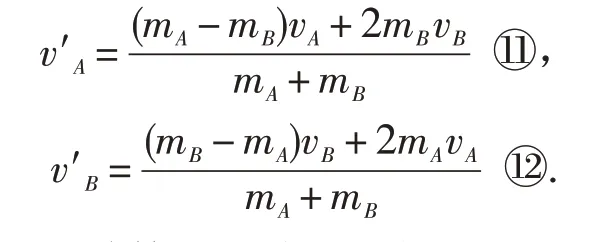
在计算一些特殊的物理问题时，对公式的记忆是有一定的快捷性，但是通过比较发现，对式子⑨、⑩记忆比⑪、⑫简单得多.因此，利用质心速度处理一维两体弹性碰撞问题不仅使问题简单化，而且对学生理解物理问题的能力和培养学生对问题的思考具有重要的意义.同理，可以把此方法延伸到其他类似的模型上，对学生的思维能力培养和解题能力的提高会有良好的效果.

2 模型迁移

物理模型是物理学科进行科学研究的重要体现，是把实际生活物体在一定条件下抽象出来，用数学等相关知识表达出来.在高中阶段的物理学习中建立模型、还原模型、迁移模型，不仅是研究物理的重要方法，同时也是培养学生的创新思维能力和发散思维的合理方式.而模型迁移是把已知的模型规律迁移到具有相同规律的模型之上，比如：学了匀变速直线运动后，再学自由落体运动，最后把两种模型应用于平抛运动，再把平抛运动模型迁移到具有相同规律的类平抛运动（带电粒子垂直进入匀墙电场的运动等）；生活中的圆周运动模型迁移到天体运动、带电粒子在磁场中的运动.模型迁移是物理研究的一种重要的科学方法，也是解决物理问题的有效方法.

迁移一：如图2 所示，光滑水平面上左端与一光滑圆弧相切，质量为9m 的物块B静止在水平面上，另一质量为m的A物块从曲面h=0.8m 的高度下滑，最后与B物块发生弹性正碰，A、B两物块可以看成质点，假设水平面足够长，请分析判断A、B物块最多能碰几次？

图2

评价:从以上的分析来看，用质心速度求解一维弹性碰撞问题，虽然也需要一定的计算过程，但是相对直接用动量守恒及能量守恒来说，应用质心速度计算时相对较为简单，而且过程也简洁.

迁移二：如图3 所示，用力压质量为0.2kg 的小球A使弹簧压缩，静止时弹性势能EP=0.4J，弹簧左端固定在墙上，右端与A接触但是不连接，B小球静止在离A较远的水平地面上，B的质量是A的3 倍，两球可以视为质点，释放A后，两小球发生弹性正碰，请计算A、B碰撞后的速度及分析A、B是否发生第二碰撞？

图3

解析：由题意，当小球A脱离弹簧时，由,所以A的速度为vA=2m/s，取向右的速度为正，则A、B组成系统的质心速度为：0.5m/s，当两小球碰撞后，由质心速度与各质点速度的关系：2vc=vA+，2vc=vB+带入数据得：=-1m/s,=1m/s.由于A、B的速度大小相等，因此A、B不会碰第二次.

评价：此模型看似简单，包含了三个重要的物理过程，弹簧与小球A组成系统的机械能守恒，A、B组成系统的动量守恒及能量守恒，这是很多学生在分析物理过程时容易弄错的过程，应用质心速度与各质点速度间的关系，这不仅培养了学生的思维能力，同时为学生在考试中赢得更多的时间，提高了解题的效率.

迁移三：如图4所示，长度为l=2m 的水平传送带左右两端与光滑的水平面等高，且平滑连接.传送带始终以2m/s的速率逆时针转动.传送带左端水平面上有一轻质弹簧，弹簧左端固定，右端与质量为mB的物块B相连，B处于静止状态.传送带右端水平面与一光滑曲面平滑连接.现将质量mA、可视为质点的物块A从曲面上距水平面h=1.2m 处由静止释放.已知物块A与传送带之间的动摩擦因数μ=0.2，mB=3mA，物块A与B发生的是弹性正撞，碰撞时间极短，碰撞后B回到原来位置时立刻锁住，重力加速度g取10m/s2.通过计算说明物块A与物块B第3次碰撞后的速度大小.

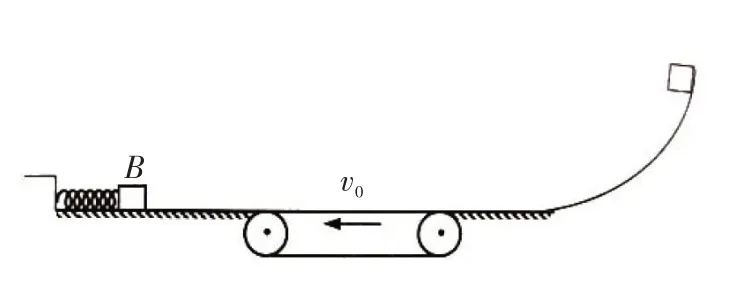
图4

解析：本题是机械能守恒、传送带问题、动量守恒、一维弹性碰撞问题，计算时分成三个阶段，曲面上的机械能守恒，传送带上的运动问题，碰撞时动量守恒.在曲面上：.在传送带上：物块受到的合外力为f=μmg，则物块在传送带上的加速度大小为a=2m/s2，由于物块在传送带上先做匀减速直线运动，有：解得：v=4m/s.

说明物块在传送带上一直做匀减速直线运动，所以A与B碰撞之前的速度大小为v=4m/s，由于A、B发生弹性碰撞，取向右为正方向，则vc=-1m/s，由-2vc=-v+vA，vA=2m/s.当A回到传送带上时做匀减速直线运动，假设A的速度减到零，有-2as=0-，解得s=1m，由于s＜l，因此A再次回到传送带左端时速度大小为=2m/s，再次与B发生弹性正碰，由质心速度与各质点速度间的关系，碰撞后A的速度大小为=1m/s，方向向右.同理可得，A、B发生第三次碰撞后瞬间A的速度大小为0.5m/s，方向向右.

评价：本题的模型虽然是与传送带结合的模型，但是与以上的模型具有相同的特点，发生弹性正碰后A球再次返回的速度特点与以上模型都一样，看似很复杂的模型，但是只要认真分析，其过程与迁移一、迁移二类似.

通过以上的分析，不难发现，解决一维弹性正碰的两体问题[2]，应用质心速度与各质点速度的关系比直接应用动量守恒及能量守恒要方便得多，同时把具有同类思想的问题模型进行联系及迁移，总结解题方法，提高解题效率.