求解Fisher市场均衡问题的内点算法
2022-09-16毕红梅刘妙华赵学军
毕红梅, 刘妙华, 赵学军
(空军工程大学基础部,西安,710051)
早些时候,Ye提出了求解Fisher市场均衡问题的原-对偶内点算法[1]。但该算法跟踪的加权中心路径并不连续,从初始可行点出发还需要通过势函数下降算法才能寻找到满足邻域要求的可行点。近年来,Potra将Fisher市场均衡问题抽象为更一般的线性权互补问题,根据已知可行点构造了一条光滑的中心路径,给出了求解线性权互补问题的内点算法[2]。当权向量为0时,权互补问题退化为一般的互补问题;对于权向量部分为0、部分大于0的情形,算法设计和分析比一般的互补问题更为复杂。自此以后,求解权互补问题逐渐成为优化领域研究热点之一。文献[3~4]设计了光滑牛顿算法求解权互补问题。文献[5]在一定假设条件下提出了线性权互补问题宽邻域的路径跟踪算法。文献[6~8]提出了求解线性权互补问题的全牛顿步内点算法。线性权互补问题来源于Fisher市场均衡模型,国内外文献重点讨论了线性权互补问题的求解方法和理论证明,算法测试大多自行设计,有些算法的设定条件并不适用于解决Fisher市场均衡这一实际问题,一些初步的研究结果可参考文献[9]。
1 Fisher市场均衡问题
在 Fisher 模型中,市场中包含消费者C和生产者P。消费者i∈C有预算wi>0从生产者手中购买商品使得个人效用函数最大化。价格均衡即给商品定价,使得每个消费者买到最多的商品,同时市场出清,即所有的预算消费完并且所有的商品销售完。不失一般性,假定生产者j有1单位的某种商品出售。
Eisenberg和 Gale证明了市场出清价格为下述优化问题的最优拉格朗日乘子[10]:
(1)
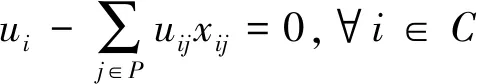
式中:uij≥0为给定的消费者i对生产者j生产商品的效应系数;xij为消费者i从生产者j手中购买的商品数量。
更一般地,式(1)可以改写成:
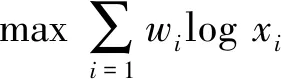
(2)
x≥0
假定最优解集非空,则式(2)的KKT 条件可以写成线性权互补问题:
Ax=b,x≥0
-ATy+s=0,s≥0
(3)
xs=w
式中:y、s分别为拉格朗日乘子。
严格可行域定义为:
F++={(x,s)>0:Ax=b,s=ATy}
给定初始严格可行点(x0,y0,s0)∈F++,令c=x0s0,构造
w(t)=(1-t)w+tc,t∈(0,1]
(4)
文献[2]将式(4)替换(3)中的第3个式子得到新的中心路径:
Ax=b,x≥0
-ATy+s=0,s≥0
xs=w(t)
(5)
当t→0时,w(t)→w得到(3)的解。
2 原-对偶内点算法
2.1 搜索方向
令γ=min (c),α=βγ, 0<β<1,定义邻域:N(α,t)={(x,y,s)∈F++:‖xs-w(t)‖≤αt}。
令t+=(1-θ)t,θ∈(0,1)。搜索方向由两个方向构成,其中仿射方向(Δax,Δay,Δas)由下面的系统给出:
AΔax=0
-ATΔay+Δas=0
(6)
sΔax+xΔas=w-xs
中心方向(Δcx,Δcy,Δcs)由下述系统给出:
AΔcx=0
-ATΔcy+Δcs=0
(7)
sΔcx+xΔcs=c-xs
仿射方向作为预测方向,中心方向作为矫正方向。本文采用的中心方向把迭代点拉向c=x0s0以保持可行性,而文献[2]中的中心方向希望迭代点向w(t)靠近。通过二分法搜索满足条件的最大θ值使得新的迭代点:
(x+,y+,s+)=(x,y,s)+(1-t+)(Δax,Δay,Δas)+
t+(Δcx,Δcy,Δcs)
(8)
属于新的邻域:N(α,t+)={(x+,y+,s+)∈F++:‖x+s+-w(t+)‖≤αt+}。
2.2 算法
算法1 线性权互补问题内点算法。
1)输入ε>0,θ∈(0,1),t0=1,初始可行点(x0,y0,s0)∈N(α,t0),令k=0。
2)若‖xksk-w‖<ε,算法停止;否则求解式(6)、(7)得搜索方向:(Δaxk,Δayk,Δask)及(Δcxk,Δcyk,Δcsk)。
3)搜索满足邻域条件的θ值θk,令:tk+1=(1-θk)tk;xk+1=xk+(1-tk+1)Δaxk+tk+1Δcxk;yk+1=yk+(1-tk+1)Δayk+tk+1Δcyk;sk+1=sk+(1-tk+1)Δask+tk+1Δcsk。
4)令k=k+1,转2)。
2.3 算法收敛性分析
算法可行需要保证新的迭代点在新的邻域内,并且随着t的减少,x+s+与w的距离不断下降,最终满足精度要求。
假定当前迭代点严格可行且满足‖xs-w(t)‖≤αt。
引理1xs≥(γ-α)te,其中e为单位向量。
证明 由xs≥w(t)-αte≥tc-αte≥(γ-α)te,即得。令:
Δx=(1-t+)Δax+t+Δcx,Δs=(1-t+)Δas+t+Δcs。则x+=x+Δx,s+=s+Δs,于是:
sΔx+xΔs=(1-t+)(w-xs)+t+(c-xs)=
(1-t+)w+t+c-xs=w(t+)-xs
(9)
进而:
x+s+-w(t+)=(x+Δx)(s+Δs)-w(t+)=
xs+sΔx+xΔs+ΔxΔs-w(t+)=ΔxΔs
(10)
引理2[11]设u,v∈Rn,uTv≥0。 记U=diag(u),V=diag(v),则‖UVe‖≤2-3/2‖u+v‖2。
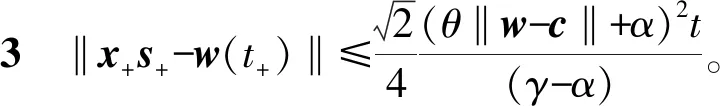
证明式(9)两边同乘以(xs)-1/2,得:
x-1/2s1/2Δx+x1/2s-1/2Δs=(xs)-1/2(w(t+)-xs)。
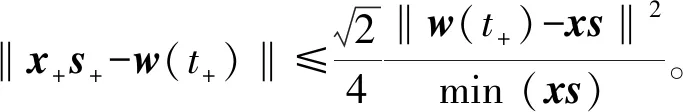
又:‖w(t+)-xs‖≤‖w(t+)-w(t)+w(t)-xs‖≤
‖w(t+)-w(t)‖+‖w(t)-xs‖≤θt‖(w-c)‖+tα。
再由引理1即得。
要使‖x+s+-w(t+)‖≤αt+=(1-θ)tα,只需
(11)
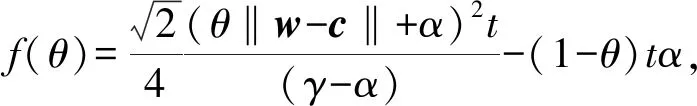
α=βγ,令β=2/3,则:
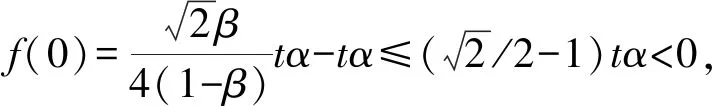
假定θ‖w-c‖≤α/8,由式(11)可计算出θ的下界为
定理1给定ε>0,初始点(x0,y0,s0)∈N(α,t0)。若系统(3)存在最优解,则算法1至多经过

证明x+s+与w的距离
‖x+s+-w‖=‖x+s+-w(t+)+w(t+)-w‖≤
‖x+s+-w(t+)‖+‖w(t+)-w‖≤(1-θ)αt+(1-θ)t‖w-c‖=(1-θ)t(α+‖w-c‖)≤(1-θ0)t(α+‖w-c‖)=(1-θ0)k(α+‖w-c‖)。
要使‖x+s+-w‖≤ε,只需(1-θ0)k(α+‖w-c‖)≤ε。
两边取对数得到:klog (1-θ0)+log (α+‖w-c‖)≤logε。
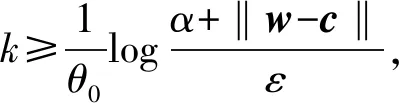
3 数值实验
本节用算法1求解Fisher 市场均衡问题。假定市场上有nc≥2个消费者,np≥2个生产者,为简单起见,不妨设nc=np=p。记e=ones(1,p),
对比式(1)、(2)可知
x=(x11,…,x1p,…,xp1,…,xpp,u1,…,up)T,
b=(e,01×p)T,其中01×p为1行p列0向量,
A为m×n=2p×(p2+p)矩阵
w=(01×p2,w1,…,wp),wi,uij,i,j=1,2,…,p在区间(0,1)中随机生成,初始点(x0,y0,s0)的取法与参考文献[1]一致。
用MATLAB R2010b编程实现算法, 用Intel Xeon2 CPU(3.3 GHz), 8 GiB ram的微机测试。当满足条件‖xs-w‖≤10-5时,算法终止。
为说明Fisher市场均衡问题求解过程,以最简单的p=2时情形为例,即市场上仅有2位消费者和2位生产者。系数矩阵A为m×n=4×6矩阵

b=[1,1,0,0],权向量即预算w=[0,0,0,0,0.957 2,0.485 4],
即2位消费者预算分别为0.957 2和0.485 4,初始点为x0=[0.5,0.5,0.5,0.5,0.471 1,0.668 7],y0=[2.871 5,2.871 5,1.523 9,1.073 5],s0=[1.652 0,2.655 3,2.418 8,1.888 5,1.523 9,1.073 5]。
用算法1求解上述问题,迭代8次,耗时0.001 3 s后得到最优解x*=[1,0,0,1,0.800 3,0.915 7],y*=[0.957 2,0.485 3,1.196 0,0.530 0],s*=[0,0.787 5,0.261 8,0,1.196 0,0.530 0]。
结果表明消费者1购买了生产者1生产的1个单位的商品,消费者2购买了生产者2生产的1个单位的商品,相应的效应系数分别为0.800 3,0.915 7,若商品价格定为1.196,0.53,对应相乘得到购买商品消费金额分别为0.957 2,0.485 4,与预算一致,商品售完,市场出清。
下面对每种规模产生10个问题,计算10次结果的平均迭代次数和平均时间。表1和表2分别给出了算法1和Ye[1]、Potra[2]算法的迭代步数和迭代时间。
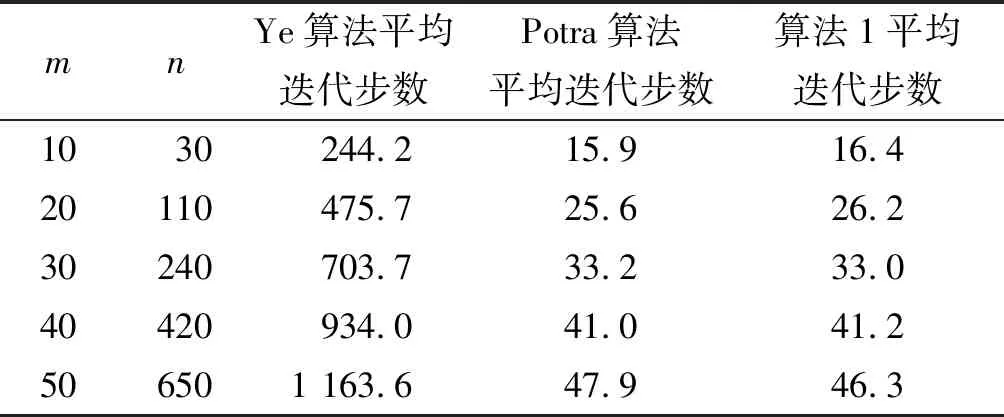
表1 Fisher均衡问题Ye、Potra及算法1迭代步数比较
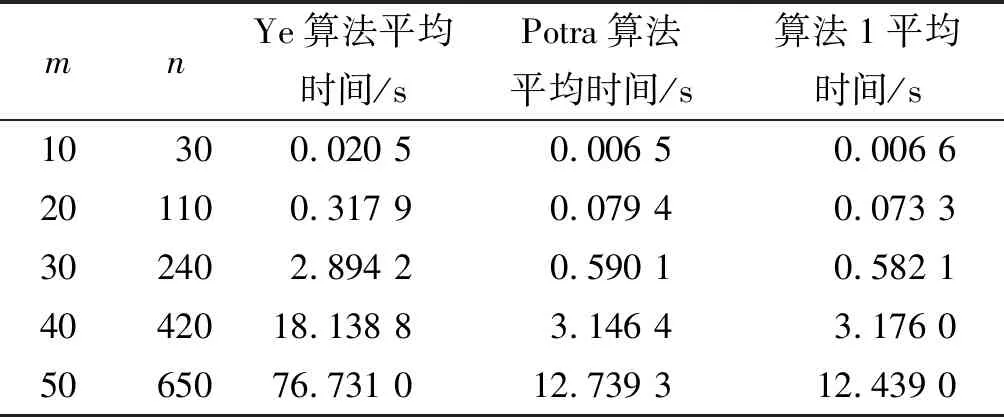
表2 Fisher均衡问题Ye、Potra及算法1迭代时间比较
由表1和表2可见,算法1与 Potra算法在迭代次数及时间上都优于Ye 算法;当问题规模达到m×n=50×650时,算法1略优于 Potra算法。
4 结语
本文从求解Fisher市场均衡这一实际问题出发,设计线性权互补问题的内点算法,就中小规模问题给出了数值结果。对于大规模问题,迭代步数和计算时间会有所增加,因此如何调节仿射方向和中心方向参数以提高算法效率,或设计更为高效的宽邻域内点算法是未来的研究重点。
