基于灰度共生矩阵的微动干扰分类识别

史崇崴，张 群*，刘治东，孙凤莲

(1.空军工程大学信息与导航学院，西安，710077；2.空军通信士官学校，辽宁 大连，116000)

随着微多普勒效应[1-3]以及微动特征提取技术[4-6]的研究与发展，利用微动特征进行目标参数估计[7]以及分类识别[8]已成为一种有效的雷达识别手段。而在逆合成孔径雷达(inverse synthetic aperture radar, ISAR)成像中，微动调制产生的微多普勒效应会导致ISAR二维成像的方位向上展宽，产生压制条带，将使目标ISAR二维图像的识别性显著下降。利用这一性质，在ISAR成像对抗中，干扰机对接收到的雷达发射信号进行微多普勒调制后再转发给雷达接收机，不仅能够在ISAR二维图像上产生压制干扰，同时还可以形成微动特征欺骗，增加了雷达利用微动特征进行目标识别的难度[9]。例如，文献[10]提出了基于合成等效微动点的ISAR干扰方法，通过对雷达信号进行正弦相位调制，改变不同干扰参数从而合成不同干扰效果的等效微动点信号，实现对ISAR成像的干扰；文献[11]提出了基于微动调制的梳状谱灵巧噪声压制干扰方法，利用雷达压缩增益降低干扰功率，同时运用微动调制特性提高了灵巧噪声干扰面积；文献[12]对目前不同体制ISAR的微动干扰方法进行了补充与研究，针对单基地ISAR提出了调制转发微动干扰、微动散射波干扰、脉冲卷积微动干扰，针对多基地ISAR提出微动散射波干扰、脉冲卷积散射波干扰，针对干涉ISAR(InISAR)提出了微动调制干扰方法、异频调制干扰方法。因此，微动干扰是一种对ISAR成像识别具有高度威胁的新型干扰方法，开展针对微动干扰样式识别的研究对提升ISAR抗干扰能力具有重要意义。

雷达干扰样式识别研究大多集中在传统的压制干扰和欺骗干扰上，而随着新型干扰样式的出现，针对新型干扰样式的识别开始得到关注。文献[13]针对多种噪声灵巧干扰和间歇采样转发干扰，提出基于自适应SSD算法和1.5维谱的识别方法，该方法在分离干扰信号特征具有优势，在低信噪比下具有较高识别率。文献[14]针对传统干扰样式以及间歇采样转发干扰、灵巧噪声干扰等新型干扰样式，提出一种基于剪枝的复数卷积神经网络进行干扰样式的识别，能有效减小运算量，同时提高识别的速度和识别率。但是，目前尚未见针对微动干扰样式识别的相关研究工作。

本文针对调制转发微动干扰、微动散射波干扰、脉冲卷积微动干扰3种微动干扰样式，提出了一种基于灰度共生矩阵的微动干扰分类识别方法。

1 微动干扰信号回波模型

假设雷达发射线性调频脉冲(Chirp)信号，则其可以表示为：

(1)

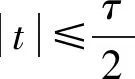
1.1 调制转发微动干扰

干扰机截获ISAR发射信号后，根据需要计算虚假微动点的相位调制信息与转发延时，对雷达信号进行包含微动信息的相位调制后，将干扰信号转发到ISAR接收机[12]。以旋转微动点P为分析对象，干扰机相位调制项可表示为：

e(tm)=σPexp (-jrPsin(ωPtm+φ))

(2)

式中：σP为P点散射系数；rP为P点旋转半径；ωP为P点旋转角速度；tm为慢时间；φ为初相。不考虑噪声影响，则P点的雷达回波可以表示为：

(3)

式中：RP表示P点与雷达之间的距离；c为光速；T=tm+t表示全时间。则干扰机经过微动调制转发后的干扰信号可表示为：

J1(t,tm)=sP(t-Δt,tm)e(tm)=

(4)

式中：Δt表示干扰机转发时延。通过改变干扰机转发时延，可以控制微动干扰条带的位置及数量，对ISAR成像产生不同程度的干扰。

1.2 微动散射波干扰

干扰机截获ISAR发射信号后，对雷达信号进行包含微动信息的相位调制，然后将干扰信号转发至目标，由目标将干扰信号散射至ISAR接收机[12]。假设雷达R与微动点P距离为PRP(tm)，干扰机T与微动点P距离为PTP(tm)，则干扰信号回波历程可以表示为：

RTPR(tm)=RRP(tm)+RTP(tm)

(5)

故微动散射波干扰信号可以表示为：

(6)

干扰机与ISAR可等效看作双基地雷达的发射机与接收机。假设等效双基角为α，由散射波信号的特性，微动散射波干扰除了在方位向上产生干扰条带外可知，还可产生与目标相似的二维像，与实际目标图像相差α/2的夹角[15]。

1.3 脉冲卷积微动干扰

脉冲卷积微动干扰的干扰原理为：干扰机截获ISAR发射信号后，利用不同延时的脉冲序列与其卷积，然后将干扰信号转发至ISAR接收机。该方法本质上是对选定距离单元内的散射点进行延时转发，通过控制转发延时参数在固定周期内循环，以实现虚假微动点回波的效果[12]。假设目标上一散射点P，则其雷达回波可表示为：

(7)

假设干扰机转发时延Δt在区间[t1,t2]上随慢时间tm循环变化，则脉冲序列可以表示为：

p(t,tm)=δ(t-Δt(tm))

(8)

式中：δ(·)表示单位冲激函数。规定f(t)=f1(t)*f2(t)表示f1(t)和f2(t)的卷积。故脉冲卷积微动干扰信号可以表示为：

J3(t,tm)=p(t,tm)*sP(t,tm)=

(9)

图1为飞机散射点模型和3种微动干扰的ISAR二维像效果图。可以看出，3种微动干扰样式均能够对真实目标回波产生压制干扰，显著增加了ISAR目标识别与跟踪的难度，因此需要对干扰进行分类识别，以采取相对应的抗干扰措施。

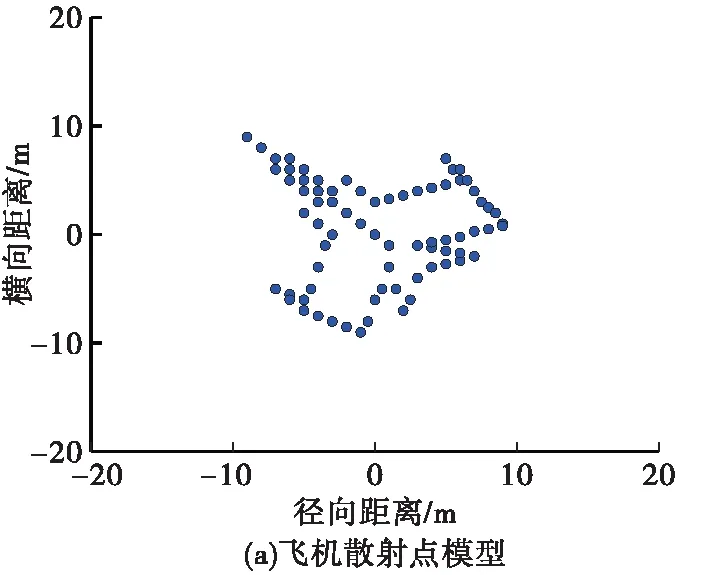
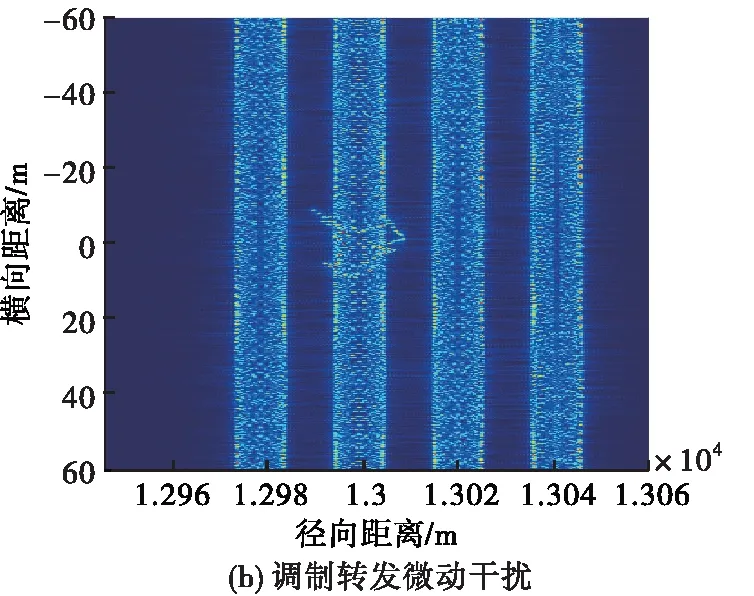
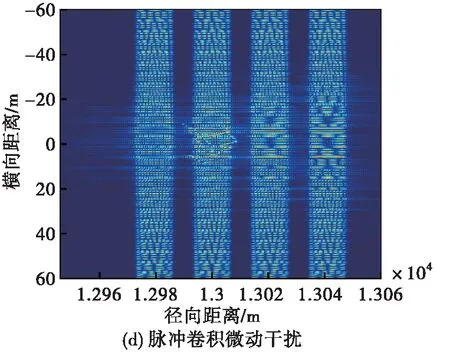
图1 散射点模型和3种微动干扰ISAR二维像

2 干扰特征提取与识别

由于微动干扰在不同脉冲间的调制参数不同，难以从单个脉冲信号中获得足够特征，本文从提取脉间特征的角度出发，从雷达接收信号矩阵的时域图像中获得不同微动干扰样式的信息进行分类识别，采用灰度共生矩阵对雷达接收信号进行分析。

2.1 回波数据预处理

在计算灰度共生矩阵前，首先对雷达接收信号进行处理。由于雷达采用线性调频脉冲信号，接收信号在|t|>τ/2的情况下值为0，因此在雷达接收信号经过解线频调处理后，对接收信号矩阵截取|t|≤τ/2的部分。接着对所截取的接收信号矩阵进行灰度化处理，具体方法为：将接收信号矩阵中的复数值取模并进行归一化处理，接着将数值扩展到0～255并取整，即可得到雷达接收信号矩阵的灰度图像。为了便于后续灰度共生矩阵的构造，减少灰度共生矩阵阶数以及运算量，同时尽可能保留灰度图原有的纹理以保证识别率，将灰度图像压缩成16级。

2.2 灰度共生矩阵原理

灰度共生矩阵(gray-level co-occurrence matrix, GLCM)是一种应用广泛的图像纹理分析方法。由于图像中相隔不同距离的两像素灰度值之间存在不同程度的关联，对这些关联进行分析可以得到图像纹理的特征。灰度共生矩阵的基本原理就是通过研究灰度图像的空间相关性质来对图像的纹理特征进行描述[16]。

灰度共生矩阵定义为：从灰度级为i的点沿着θ方向，以d作间隔距离,到达灰度级为j的点的概率，记作Pd,θ(i,j)。假设L表示图像的灰度级，有i,j=0,1,…,L-1；M，N分别表示图形像素点的行数和列数；l(x,y)表示坐标为(x,y)的点所对应的灰度级。一般情况下，取θ={0°,45°,90°,135°}，则从l(x1,y1)=i到l(x2,y2)=j在4个方向上的灰度共生矩阵元素表达式为：

(10)

式中：#表示满足限制条件的像素点对的个数。为了便于提取纹理特征参数，将矩阵归一化处理：

(11)

式中：Pd,θ表示归一化后的灰度共生矩阵；R表示归一化系数，其值为灰度共生矩阵的所有元素和：

(12)

则归一化后的灰度共生矩阵各元素可表示为：

(13)

将处理后的雷达接收信号矩阵灰度图像依据上述方法处理，可以得到其4个方向的灰度共生矩阵，以便进行下一步的特征提取。

2.3 纹理参数特征提取

在按照上述方法生成归一化灰度共生矩阵的基础上，可以进一步分析二次统计量，提取图形的纹理参数[17]。本文采用了以下4种纹理参数提取特征。

1)角二阶矩

角二阶矩(angular second moment, ASM)是灰度共生矩阵所有元素的平方和，也称为能量，可表示为：

(14)

角二阶矩反映了图像的灰度分布均匀程度和纹理粗细度。ASM值越大，表明图像的纹理变化越规则和均匀。因此对于雷达接收信号矩阵灰度图，其纹理越粗，ASM越大；纹理越细，ASM越小。

2)熵

熵(entropy, ENT)能够度量图像包含纹理信息量的大小，是一种随机性的度量，可表示为：

(15)

熵反映了图像纹理的复杂程度或非均匀度。对于雷达接收信号矩阵灰度图，当其灰度共生矩阵中的元素取值分布不均匀时，表明图像纹理较简单、灰度均匀，ENT取值较小；反之，ENT取值较大。

3)对比度

对比度(contrast, CON)是灰度共生矩阵主对角线附近的惯性矩，可表示为：

(16)

对比度反映了图像的清晰度和纹理沟纹深浅的程度。对于雷达接收信号矩阵灰度图，当其视觉效果较清晰，纹理沟纹较深时，则CON取值较大；反之，CON取值越小。

4)相关

相关(correlation, COR)用于度量灰度共生矩阵元素在行或列方向上的相似程度，可表示为：

(17)

式中:μx、μy、σx和σy分别定义为：

(18)

(19)

(20)

(21)

对于雷达接收信号矩阵灰度图，当其灰度共生矩阵的元素值均匀相等时，图像具有方向性的相似纹理区域，此时COR取值较大；反之，COR取值较小。

利用构造的4个方向的灰度共生矩阵纹理参数求取均值和标准差，则每种纹理参数可得到2个特征参数，一共可以得到8个特征参数。

2.4 微动干扰样式分类识别步骤

综上所述，本文提出的微动干扰样式分类识别的具体步骤如下：

步骤1对雷达接收信号矩阵进行预处理，获得其灰度图像；

步骤2利用式(10)～(11)构造灰度图像4个方向的灰度共生矩阵；

步骤3利用式(14)～(17)计算角二阶矩、熵、对比度、相关等4个纹理参数，分别求纹理参数4个方向的均值和标准差，获得8个特征参数，并构造特征向量；

步骤4将特征向量输入KNN分类器，从而实现微动干扰样式的分类识别。

3 仿真结果与分析

3.1 数据集设计

本文仿真参数设置如下：假设雷达发射线性调频脉冲信号，载频10 GHz，带宽400 MHz，脉宽5 μs，脉冲重复频率200 Hz，脉冲数量512个。雷达对如图1(a)所示的飞机散射点目标发射信号，采用ISAR转台成像模型，假设目标距离雷达13 km，转动角速度为0.02 rad/s。依据雷达是否受到干扰以及不同的微动干扰类型，将雷达接收信号分为以下4类：

(22)

式中：s0(t,tm)为目标回波信号；J1(t,tm)为调制转发微动干扰信号；J2(t,tm)为微动散射波干扰信号；J3(t,tm)为脉冲卷积微动干扰信号；n(t)为高斯白噪声。针对这4类雷达接收信号进行数据集设计，分别在信噪比(SNR)为5 dB, 0 dB, -5 dB的情况下进行仿真。具体干扰参数范围如表1所示，在此范围内每种干扰选取10组不同参数，参数取值尽量随机分散。4种雷达接收信号分别在干信比(JSR)为-5 dB～15 dB的情况下，每组参数每隔1 dB做20次蒙特卡洛实验，其中前10次实验数据用于训练，后10次实验数据用于测试。则在每种信噪比下，4种雷达接收信号总共有4×21×10×20=16 800个样本，其中训练集8 400个样本，测试集8 400个样本。

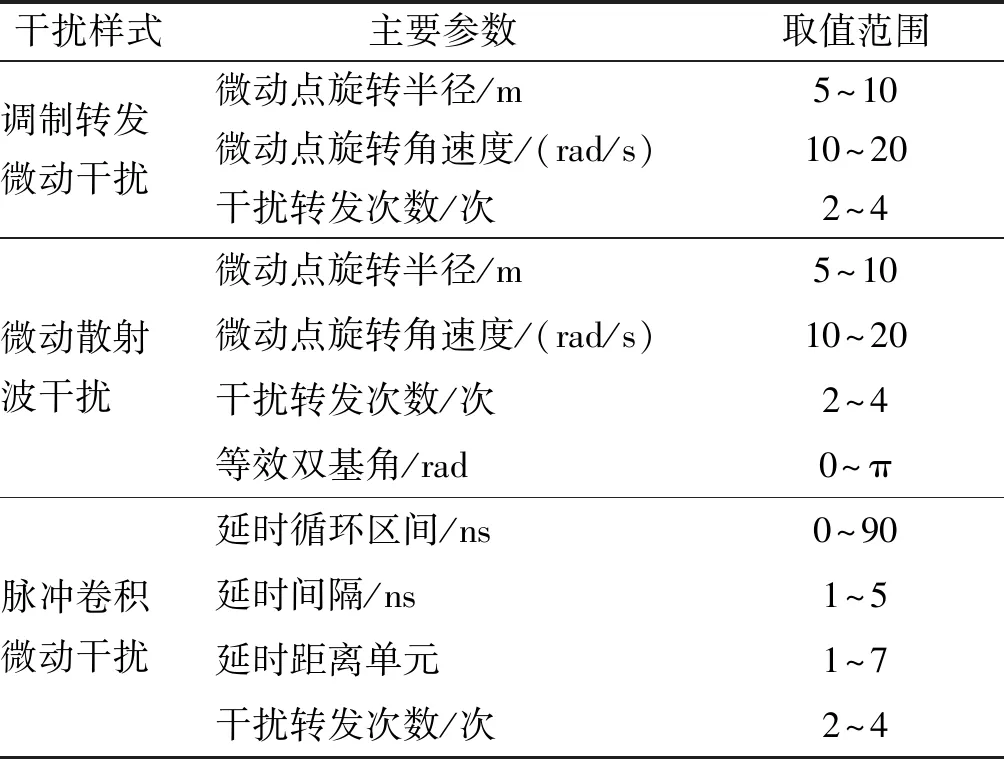
表1 干扰参数设置

3.2 特征参数仿真分析

选择SNR=5 dB条件下的训练集作为特征参数仿真分析的对象,构造间隔距离d为1，灰度级为16级，θ={0°,45°,90°,135°}的4个灰度共生矩阵，提取所选训练集在不同JSR下的角二阶矩、熵、对比度和相关4个纹理参数的样本均值，并对纹理参数的4个方向求均值和标准差，产生8个特征参数，仿真结果如图2所示，图例表示皆相同。

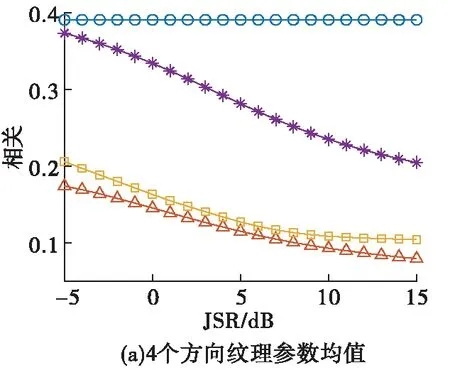
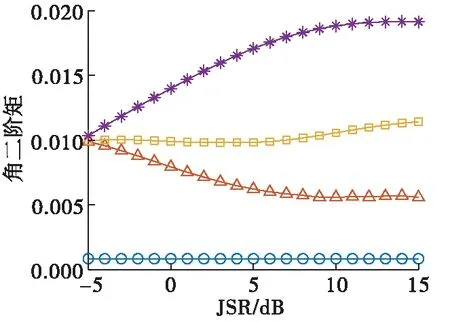
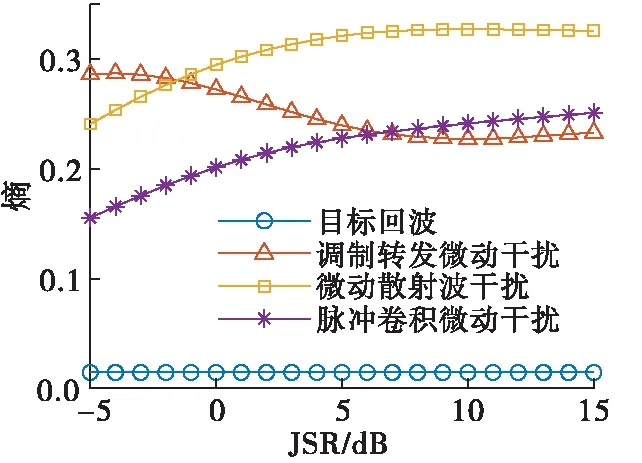
图2 特征参数随JSR变化曲线

如图2(a)所示，4个方向纹理参数均值中，角二阶矩、对比度2个特征参数能够有效地将4种雷达接收信号分成2类，但是目标回波和脉冲卷积微动干扰、调制转发微动干扰和微动散射波干扰却难以区分。熵、相关这2个特征参数能够在JSR较大的情况下实现目标回波与脉冲卷积微动干扰的有效分离。此外，熵还能够在低JSR下区别调制转发微动干扰和微动散射波干扰。

如图2(b)所示，4个方向纹理参数标准差中，角二阶矩、熵、对比度3个特征参数均能够对目标回波信号与干扰信号进行分离，相关能够在低JSR下有效区分目标回波信号和干扰信号。在此基础上，角二阶矩能够在JSR较大的情况下，实现对4种雷达接收信号的分离，但是低JSR下3种干扰信号难以区分；熵能够在JSR较大的情况下对调制转发微动干扰和微动散射波干扰进行分离；对比度能够将脉冲卷积微动干扰信号与另外2种干扰信号区别开；相关能够在低JSR下区分调制转发微动干扰和微动散射波干扰。

综合所提取的4种纹理参数的4个方向的均值和标准差共计8个特征参数，能够对目标回波和3种微动干扰信号进行有效的区分，因此联合这8个特征参数用于雷达接收信号的分类识别将有较好的效果。

3.3 识别结果与分析

根据上文所提取的8个特征参数，将其组成特征向量，利用分类器对SNR=5 dB, 0 dB, -5 dB情况下的雷达接收信号数据集样本进行分类识别，其中训练集用于训练分类器，测试集用于测试分析识别结果。考虑到在本文数据集样本足够的条件下，同时存在噪声干扰情况可能会造成样本特征参数产生交叉或重叠，选择KNN分类器相较于其他分类器例如支持向量机、决策树等更合适且精度更高。KNN分类器的参数设置如下：K值取1，距离度量选取欧氏距离，仿真结果如图3所示。

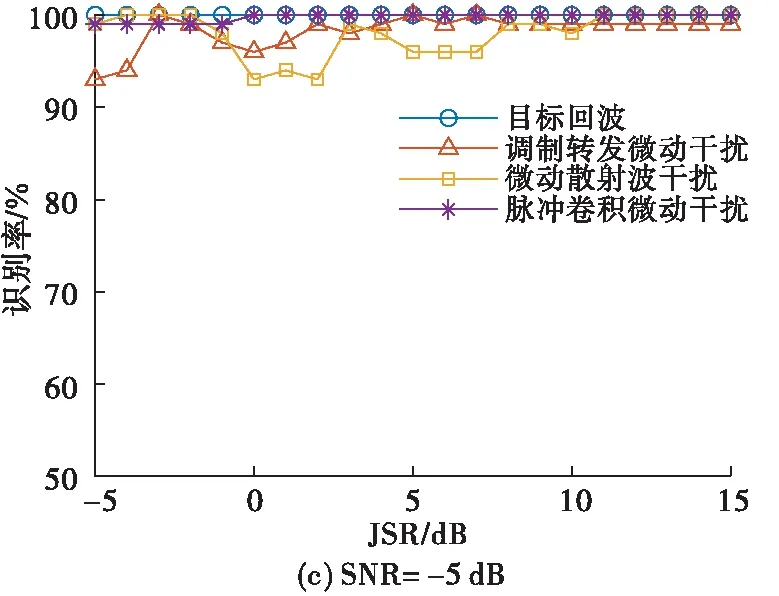
图3 干扰识别率随JSR变化曲线

由图3可知，在SNR=5 dB的情况下，雷达接收信号识别率整体较为稳定，在JSR的变化区间范围内能够达到95%以上，目标回波和脉冲卷积微动干扰能够保持100%的识别率。在JSR≥0 dB时，4种不同雷达接收信号的识别率几乎能够稳定在100%。

在SNR=0 dB的情况下，调制转发微动干扰在JSR取-5～0 dB时识别率较SNR=5 dB情况下有一定程度的下降，但是整体来看，随着JSR的增加，其识别率也在提升。在JSR≥5 dB时，4种不同雷达接收信号的识别率能够稳定在100%。

在SNR=-5 dB的情况下，识别性能出现了较明显的波动与下降，其中目标回波和脉冲卷积微动干扰的识别率较为稳定，在JSR的变化区间范围内能保持在99%以上，而微动散射波干扰在JSR取-1～8 dB范围内出现了较明显的波动，而调制转发微动干扰随着JSR的增加，识别率整体在提高，最后稳定在99%。在JSR≥8 dB时，4种不同雷达接收信号的识别率能够保持在98%以上。

综上所述，提高JSR能够提高识别的准确率与稳定性。对比不同SNR下的识别率，可知该方法具备一定的抗噪能力，在SNR=-5 dB的情况下仍然具备良好的识别率。同时该方法在低JSR下也具有良好的识别性能，在SNR=-5 dB时，在低JSR变化范围内的最低识别率仍能够保持90%以上，识别率较高。不同信号样式在不同SNR下整体的识别率，如表2所示。

表2 不同SNR下信号样式的识别率 单位：%

当SNR分别取-5 dB，0 dB，5 dB时，每种雷达接收信号样式在JSR取-5 dB～15 dB的变化范围内，总体识别率可以达到98%以上，其中目标回波能够稳定在100%的识别率。当SNR=5 dB时，每种信号样式的识别率均在99%以上。由此可见，该方法对于目标回波和3种微动干扰样式具有良好的识别性能。同时由于数据集设计时，选取各信号样式的10组不同参数，并且兼顾参数分布范围的分散性，因此该方法具有较好的泛化能力。

4 结语

针对目标无干扰回波和调制转发微动干扰、微动散射波干扰、脉冲卷积微动干扰3种微动干扰样式的识别问题，本文提出一种基于灰度共生矩阵的干扰识别方法。该方法通过对雷达接收信号矩阵进行灰度化处理，提取其4个方向灰度共生矩阵的角二阶矩、熵、对比度、相关等4个纹理参数的均值和标准差作为特征参数，并采用KNN分类器实现对4种信号样式的识别。仿真结果表明，该识别方法具有良好的识别准确性和抗噪性能。本文仅考虑了对3种微动干扰样式进行识别，下一步可针对更多微动干扰样式以及其他新型干扰样式开展分类识别研究。