基于支持向量回归的新型胎儿体重预测模型的研究

2022-09-16林燕茹唐文波庄佳衍

中国妇幼健康研究 2022年9期

刘腾，朱屹，林燕茹，朱琴，唐文波，庄佳衍

(1.宁波大学医学院附属医院，浙江宁波 315020；2.中国科学院宁波工业技术研究院，浙江宁波 315201；3.宁波大学，浙江宁波 315211)

胎儿体重预测是产前管理的重要内容，准确的胎儿体重预测可以减少围产儿的患病率、死产率、死亡率及孕产妇并发症。在临床工作中，准确的胎儿体重预测显得尤为重要。在过去的30年中，对胎儿体重预测模型的研究有几十种之多。目前准确性最高、临床最常用的仍然是1985年Hadlock等报道的基于超声测量数据所建立的回归模型。据报道该模型对胎儿体重预测准确率(出生体重±10%)只有67%～86%[1-8]。当然也有基于临床数据(孕妇宫高及腹围)的胎儿体重预测模型，其预测的准确性更低，仅占55.0%～74.3%[5，9]。2017年，国际胎儿和新生儿生长联盟尝试构建一个通用的胎儿体重预测模型，即Intergrowth-21st模型[10]。有研究表明其预测准确率为57.6%～72.6%[11-13]。可见，胎儿体重预测的准确性有待提高。近年来，为了提高胎儿体重预测准确率，有研究已将目光转移到三维超声[11，14-15]及磁共振[16-17]检查方面。虽然三维超声和磁共振检查从一定程度上提高了预测准确率，但仍不理想。考虑三维超声和磁共振检查并非常规测量，且费用较高，耗时较长，目前难以普遍推广应用。因此，如何应用更为全面的孕妇生理参数和超声参数，建立一种比较简便同时又较传统方法更加准确和个性化的胎儿体重预测方法，将估计胎儿体重的误差减小至产科临床可接受范围内，仍是亟待解决的重大挑战。

随着人工智能技术的不断发展，使进一步提高胎儿体重预测的准确性成为了可能。支持向量回归(support vector regression，SVR)[18]是机器学习算法的一种，是一种模仿人脑的非线性信息处理系统。该方法通过数学建模的方式模拟人类的学习过程，可用于真实结果的预测。因此，本研究尝试联合应用临床数据及超声数据，拟构建一种方便、经济且性能良好的基于SVR的新型胎儿体重预测模型(简称新模型)。

1 研究对象与方法

1.1 研究对象

1.1.1 数据的收集及临床数据库的建立

收集2020年1月至6月在宁波大学医学院附属医院分娩的1 442例孕产妇(限单胎头位孕晚期)的临床资料，于分娩前1周内采集相关数据，最大可能地减少误差。收集的数据共计18维，包括3个方面，①母亲数据：年龄、孕周、胎产次、身高、体重、宫高、孕妇腹围、孕期增重、是否妊娠期糖尿病(gestational diabetes mellitus，GDM)、分娩方式(顺产/产钳/剖宫产)等；②超声测量的胎儿数据：双顶径、头围、股骨长、胎儿腹围、羊水指数；③胎儿情况：胎头是否入盆(未入盆/浅入盆/入盆)、性别、出生体重。

1.1.2 纳入标准

单胎，头位，妊娠31～42周，有明确的末次月经或可依据早孕期超声测量头臀长度确定孕周，中孕期大畸形筛查未见胎儿结构异常。本研究经宁波大学医学院附属医院伦理委员会批准(批件号KY20201121)。所有参与本研究的纳入对象均签署知情同意书。

1.2 机器学习算法的选择

分别应用以下方法对现有数据进行预实验，通过对比选出最优的算法。

①基于多层感知机的反向传播算法(Back Propagation)：通过随机变量的多元线性组合和非线性函数激活，从而拟合目标函数，并通过误差反传，迭代调整多层感知机的参数权重，自动学习最佳的映射函数；②决策树回归(Regression Tree)：通过寻找样本中最佳的特征及特征值作为最佳分割点，构建一棵二叉树，在预测阶段，根据提供的样本特征，以叶子节点的值作为预测值；③多元线性回归(Multivariable Linear Regression)：通过2个或2个以上的影响因素作为自变量解释因变量的变化；④轻量梯度提升机(Light Gradient Boosting Machine)：简称LightGbm，其为一种集成学习方法，通过合并多个决策树构建一个更为强大的模型，采用连续的方式构造树，每棵树都试图纠正前一棵树的错误；⑤SVR：在支持向量机(Support Vector Machine，SVM)的基础上，将最大化分类间隔的分类任务替换为最大化回归范围的回归任务的变种。

1.3 构建基于SVR的新模型

1.3.1 选出建模参数

根据预实验结果，分别计算每个特征与新生儿出生体重的皮尔逊相关系数，应用SVR算法权重，结合临床经验，反复进行实验后，根据实验结果选择建模所需的参数。

1.3.2 应用SVR建模

SVR算法是在SVM基础上发展起来的一种自回归算法。SVM算法是利用核函数的方法，将在低维特征空间线性不可分的样本映射到更高维特征空间，使得线性可分。

SVR算法是建立在SVM理论基础上的一种回归算法，给定数据集D={(x1,y1),(x2,y2),…,(xm,ym)|m∈R}，学习目标回归函数f(x)，f(x)=wTφ(x)+b，其中φ(x)为非线性映射函数[12]。以学习到的函数f(x)为回归中心，构建一个宽度为2ε的间隔带，若测试样本落入此间隔带，则认为是被预测正确的样本。

1.3.2.1 数据的预处理数据预处理是数据挖掘分析的基础，主要分析数据来源，对数据进行采集、清洗、规整，实现对数据的规范化，为之后的数据分析打下良好基础[19]。对新生儿出生体重预测问题主要采集的数据：一是孕妇相关数据；二是B超数据；三是胎儿相关数据。

针对采集的数据，需要进一步进行处理。①离散数据的数值化：对采集数据中的是否GDM进行数值化，应用Python语言对其进行处理，将有GDM标记为0，无GDM标记为1；②异常值处理：在采集到的数据中，不免会出现数据缺失、异常等情况，对于缺失的数据，首先引入Python语言的一个扩展程序库Pandas，其是一个强大的分析结构化数据的工具集，应用Pandas中的read excel()方法来读取数据文件，并应用数据处理工具包NumPy(Numerical Python)进行数据清洗，踢除含有空值的数据。

1.3.2.2 模型的构建数据集经过预处理后进行划分，应用sklearn.model selection中的train test split函数将原始数据集划分为训练集和验证集，且划分比例为9∶1。SVR模型中核函数的主要作用是将高维数据映射为低维数据，常见的核函数有‘rbf’‘linear’‘poly’，实验对比后选择应用linear核函数，应用该核函数在训练集上可以更好地拟合数据，见图1。同理，惩罚因子C在超参数调优后设为1.35。将收集到的数据以90%用于训练，而10%用于验证。损失函数选用平均绝对误差(mean absolute error，MAE)。构建出基于SVR的新模型。

1.3.2.3 模型的评估将新模型与经典胎儿体重预测模型(Hadlock1模型和Intergrowth-21st模型)对比，比较平均绝对百分比误差(mean absolute percentage error，MAPE)、MAE、均方根误差(root-mean-square error，RMSE)及胎儿体重预测准确率来评估每个模型的胎儿体重预测的准确性，评估新模型的性能。

MAPE=(|预测体重值-实际体重值|)/实际体重值×100%。计算预测体重与实际出生体重误差的绝对值占实际出生体重的百分比，求其平均值及标准差，可准确评估误差的大小。

MAE=|预测体重值-实际体重值|。直接计算预测体重与实际出生体重误差后进行平均，平均值和标准差均以g为单位，与原始数据量纲一致，便于直接进行比较。

RMSE为回归分析中常用的评价指标，常出现于应用回归分析等方法的研究中，可准确评估误差的大小，且量纲与原始数据相同，便于直接比较。

将预测体重与实际出生体重MAE在250g以内定义为预测准确；5%预测准确率是指预测体重与实际出生体重之间误差不超过5%实际出生体重，10%预测准确率是指预测体重与实际出生体重之间误差不超过10%实际出生体重。预测准确率(%)=成功预测数量/总数量×100%。

1.4 统计学方法

应用的计算工具基于Python 3.7语言，其中包括数据处理工具NumPy 1.19.5和Pandas 1.3.5及数学建模工具Scikit-learn 1.0.1。Pandas用来读取数据文件；应用NumPy进行数据清洗，剔除异常样本，对数据进行处理及统计；采用Scikit-learn对处理后的数据进行数学建模。

2 结果

2.1 孕产妇的基本资料

本研究选取了2020年上半年间符合纳入标准的孕产妇共计1 442例，总共纳入18维参数，其中GDM孕产妇242例，其他孕产妇1 200例；经阴道分娩824例，剖宫产618例；孕次为1～8次，平均(1.95±1.16)次；初产妇948例，二胎分娩475例，三胎分娩19例；男婴747例，女婴695例；其余纳入的14维参数及总体样本的均值见表1。

表1 孕产妇的基本资料及数据范围Table 1 The basic data and data scope of pregnant women

2.2 应用预实验选出最优算法SVR

应用基于多层感知机的神经网络、决策树回归、多元线性回归、LightGbm、SVR算法对现有数据进行预实验，共计18维，有效数据1 442条，其中1 297条作为训练数据，145条作为测试数据，计算MAPE、MAE、RMSE及胎儿体重预测准确率。

LightGbm算法的10%误差预测准确率最高，Linear-Regression算法的250g误差预测准确率最高，SVR算法的5%误差预测准确率最高，且SVR算法有最小的MAPE、MAE和RMSE。LightGbm算法在寻找最优解时，依据的是最优切分变量，未将最优解受所有特征综合影响考虑进去，多元线性回归算法对于数据特征间具有相关性多项式回归难以建模，BP算法预测精度不高。对于特征维度少的数据，SVR不易造成过拟合，添加的松弛变量可以提高模型的泛化性。LinearSVR应用线性核函数，在实验过程中难以收敛；NuSVR预测MAE较SVR低。因此选择SVR作为预测算法。

观察实验结果发现，在应用全部数据的条件下，不同算法得到预测模型的预测性能指标见表2。

2.3 应用SVR建立新模型

2.3.1 选出建模参数

分别计算每个特征与新生儿出生体重的皮尔逊相关系数，其中，P值作为判断变量之间是否存在相关性的指标，当P>0.05时，相关性系数无统计学意义，即该特征与观测值无相关性；当P≤0.05时，表示两者具有相关性，此时r值越大，代表相关性越高，两者间的线性相关性越大。如：B超胎儿腹围数据P值接近0，说明该特征与观测值显著相关。新生儿性别的r值为负数，该特征与观测值呈负相关。

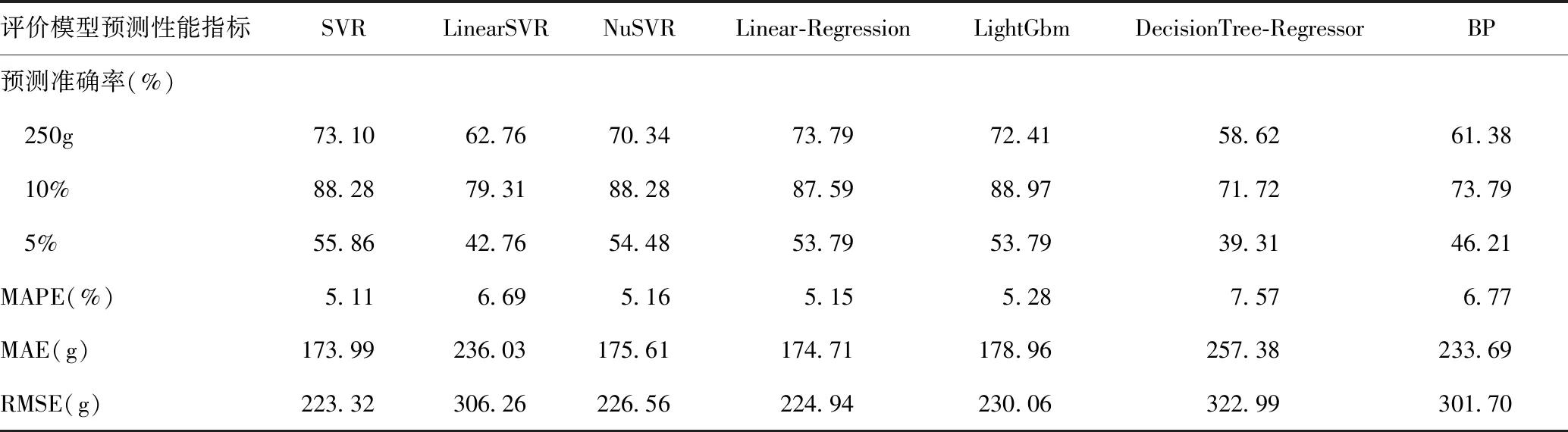
表2 不同算法的预测准确率及预测误差Table 2 The prediction accuracy and error of different algorithms

根据皮尔逊相关系数的结果，P>0.05表明该特征与新生儿出生体重相关性小，因此孕妇年龄(r=0.03，P=0.19)不予采用；考虑在收集数据时对采集时间有1周内的限制，因此采集时间(r=0.01，P=0.77)予以保留；是否为GDM(r=-0.05，P=0.04)中P值接近0.05，且r值很小，因此不予采用；虽然胎儿性别(r=-0.12)、分娩方式(r=0.15)、孕次(r=0.06)、产次(r=0.07)的P<0.05，但其r值均较小，且胎儿性别及分娩方式在出生前临床上无法获知，因此这些特征不予采用，见表3。根据皮尔逊相关性分析，虽然分娩孕周相关性相对尚可(r=0.42，P=4.56×10-64)，但考虑到临床应用的方便，不便采纳过多的参数，因此分别应用包含12维特征及去除分娩孕周的11维数据进行建模，结果显示两者的预测误差在250g以内分别为72.41%和73.10%，因此，分娩孕周不予采用。

最后筛选出建模所需的11维参数分别为：身高、体重、孕期增重、宫高、孕妇腹围、双顶径、头围、股骨长、胎儿腹围、羊水指数和采集时间(采集时间距分娩的天数)。

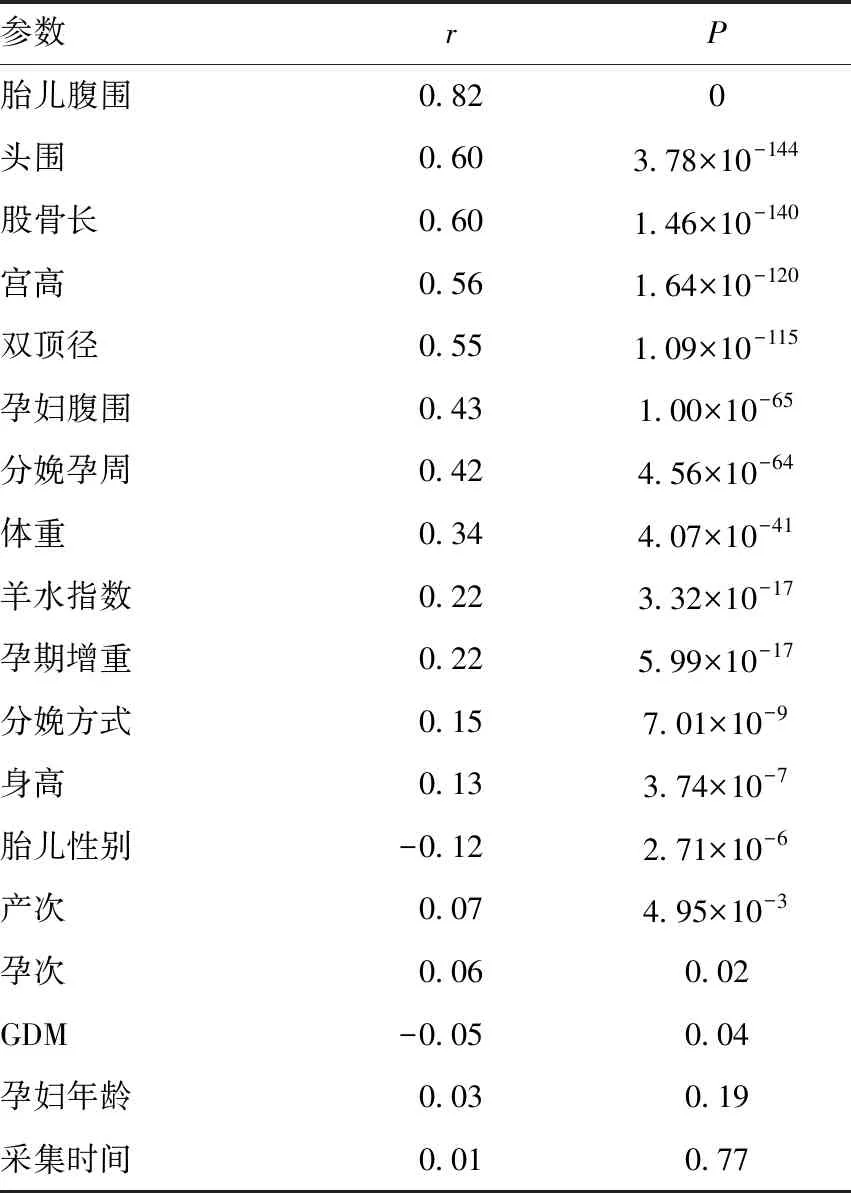
表3 新生儿出生体重与不同参数的皮尔逊相关系数Table 3 Pearson correlation coefficient between newborn birth weight and different parameters

应用SVR算法对11维参数进行权重对比，数值越大表示参数影响越大，本资料显示宫高的SVR权重最大，说明在新模型中影响最大，见表4。

表4 纳入建模参数的SVR算法权重对比Table 4 Weight comparison of the SVR algorithm incorporating the modeling parameters

2.3.2 构建新模型

应用SVR对筛选后的11维参数及18维参数分别建模，并对其建模结果进行对比。应用18维参数构建的模型10%预测准确率与应用11维参数构建的模型预测准确率相同，均为88.28%，从MAPE、MAE及RMSE方面而言差别也较小；换而言之，应用18维与11维两种参数建模所得到的预测模型在预测性能方面相差无几，见表5。考虑临床应用的实际情况，不宜选择过多的参数，因此选择应用11维参数构建的模型为新模型。

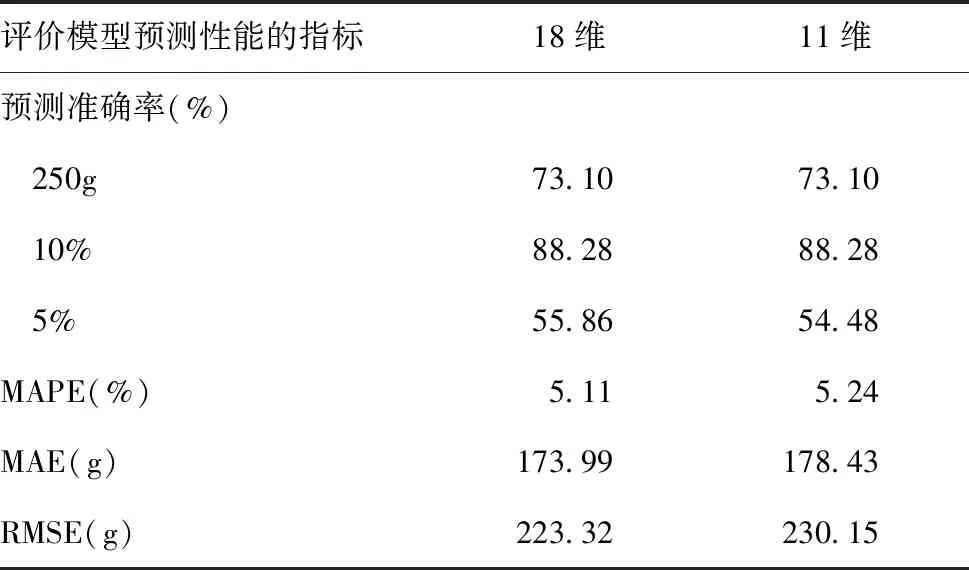
表5 应用不同维度参数建模的性能对比Table 5 Performance comparison of modeling with different dimension parameters

2.4 评估新模型性能

将新模型与经典胎儿体重预测模型(Hadlock1模型及Intergrowth-21st模型)对比，以MAPE、MAE、RMSE及胎儿体重预测准确率评估新模型的性能。与Hadlock1及Intergrowth-21st模型相比，预测误差在5%以内的胎儿体重预测准确率为54.48%、预测误差在10%以内的为88.28%、预测误差在250g以内的为73.10%，新模型具有最高的胎儿体重预测准确率。此外，胎儿体重预测新模型还具有最低的MAPE(5.24%)、MAE(178.43g)、RMSE(230.15g)，见表6。

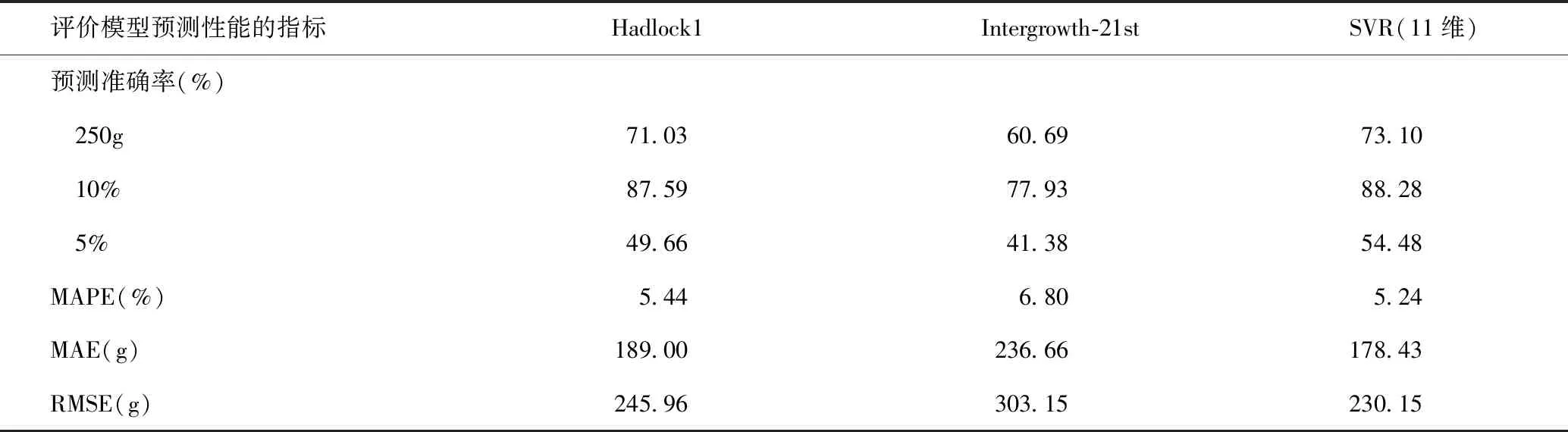
表6 新模型与经典模型的对比Table 6 Comparison of the new model and the classical model

3 讨论

3.1 新模型的预测性能及原因分析

本研究表明，与Hadlock1模型及Intergrowth-21st模型相比，新模型具有最高的胎儿体重预测准确率，即54.48%胎儿的预测体重与实际出生体重之间误差不超过5%，88.28%胎儿的预测体重与实际出生体重之间误差不超过10%，73.10%胎儿的预测体重与实际出生体重差距在250g以内。另外，新模型还具有最低的MAPE(5.24%)、MAE(178.43g)和RMSE(230.15g)，说明新模型预测误差最小。因此，新模型具有最优的预测性能。

本研究显示，Hadlock1模型比Intergrowth-21st模型的预测准确率高(87.59%，77.93%；<10%)，预测误差小(189.00g，236.66g；MAE)，这与既往的研究结论[20]相符合，即基于3～4个参数预测模型较1～2个参数预测模型的预测准确率高，误差小。既往研究表明，不同超声医师[21]测量、胎先露不同[22]、羊水量[23-25]、孕产妇肥胖[26-27]等都会影响胎儿超声体重预测模型的准确性[20，27-28]。而Hadlock1模型仅仅是基于超声测量的胎儿双顶径、股骨长、头围及腹围，未联合羊水指数、临床数据等参数，且在建模时应用线性回归的方法。这些可能就是其预测准确率有待提高的原因。

3.2 SVR的优势

机器学习与传统的参数回归模型相比有着不可替代的优越性，可以进行自动化学习，以任意精度逼近任意复杂的非线性映射[19]。因此，本研究将机器学习算法引入胎儿体重预测模型，使得联合多维参数构建胎儿体重预测模型成为可能。为了构建最佳的新模型，本研究从以下几方面做出了努力。首先，新模型联合了多维参数，弥补了既往模型参数较少的缺点；其次，通过预实验，对比不同的机器学习算法，从而选出最适合的机器学习算法，即SVR；最后，如何选择合适的建模参数，即如何才能应用最少维度的参数得到最佳的预测性能也是本研究的重点。

本研究初期收集了尽可能全面的18维参数，考虑数据中可能存在混杂因素，因此计算每个参数与新生儿出生体重的皮尔逊相关系数，相关性小的参数不予采用，最终得到建模所需的11维参数，包括：身高、体重、孕期增重、宫高、孕妇腹围、双顶径、头围、股骨长、胎儿腹围、羊水指数及采集时间(采集时间距分娩的天数)。为了进一步验证应用11维参数构建模型的预测准确率，本研究对11维参数模型与18维参数模型进行了对比，结果显示应用11维参数构建的新模型与18维参数构建的体重预测模型在预测准确率及误差等方面相差无几。因此，本研究最终决定应用11维参数构建胎儿体重预测模型。本研究所纳入的11维参数均是临床病例书写所必需采集的数据信息，本研究构建的新模型在未来可以直接植入电子病例系统，从电子病例中对所需数据进行提取，从而直接得到预估的胎儿体重，以供临床参考。