基于SOA-LSSVM的SLS成形工艺参数优化研究

2022-09-16肖亚宁孙雪张亚鹏裴玲艺李三平

机床与液压 2022年6期

肖亚宁，孙雪，张亚鹏，裴玲艺，李三平

(东北林业大学机电工程学院，黑龙江哈尔滨 150040)

0 前言

选择性激光烧结(Selective Laser Sintering，SLS)是一种基于三维模型离散-材料堆积成形原理的快速增材制造技术。相比于传统加工制造，选择性激光烧结加工过程中无需刀具、成形模具就可以制造出复杂结构零件，有效控制了生产成本，缩短研发周期。然而，选择性激光烧结技术是一种复杂的热物理化学过程，不同的工艺参数组合以及粉末特性导致成形件精度难以得到有效控制，限制了其进一步实际发展和市场应用。

目前，国内外学者主要通过试测法以及BP神经网络算法建立预测模型来获取制件精度。所谓“试测法”是利用专家经验制定一组较优的工艺参数，这种方法周期长、成本高。刘硕等人将正交试验结果作为训练样本，建立基于广义回归神经网络的选择性激光烧结制件精度预测模型。任继文等利用BP神经网络，研究SLS工艺参数与烧结宽度和深度之间的定量关系。王丹妮等利用粒子群优化算法改进BP神经网络模型，建立制件尺寸精度的预测模型，但由于BP算法本身收敛速度慢、待寻优的参数多，预测精度有待提高。

最小二乘支持向量机(Least Square Support Vector Machines，LSSVM)作为一种新兴的机器学习算法，能更好地解决小样本、非线性等实际问题。最小二乘支持向量机在传统支持向量机的基础上，将不等式约束转化为等式约束，避免了复杂的二次规划问题，计算效率更高，但LSSVM模型预测精度取决于核函数参数以及惩罚系数。人群搜索算法(Seeker Optimization Algorithm，SOA)作为一种新型启发式仿生算法，采用全局优化方法，其收敛速度快、精度高，在参数寻优上得到广泛应用。

本文作者选取激光功率、预热温度、扫描速度、扫描间距以及分层厚度作为SLS工艺参数的研究对象。设计正交试验，建立基于SOA-LSSVM的选择性激光烧结成形件精度预测模型；利用SOA寻找LSSVM模型的核函数参数和惩罚系数最优组合；对成形件统一性能进行预测并分析确定最优参数组合，与优化前的LSSVM模型以及BP神经网络对比，结果表明：SOA-LSSVM算法预测精度更高，对选择性激光烧结成形工艺参数组合的选取有积极意义。

1 选择性激光烧结试验

1.1 样本数据的获取

影响SLS成形件精度的工艺参数主要包括激光功率、预热温度、扫描速度、扫描间距和分层厚度。

此次试验选用自主设计的CX-A200激光烧结快速成形机，主要技术参数：最大功率40 W，成形尺寸200 mm×200 mm×200 mm，分层厚度0.08～0.2 mm，最大扫描速度3 500 mm/s，输入文件格式为GCODE。

试验设计采用150 mm×20 mm×4 mm的标准测试样件为模型，如图1所示。试验材料为聚苯乙烯(PS)，选择激光功率、预热温度、扫描速度、扫描间距以及分层厚度为正交试验的因子，每个因子水平选择如表1所示，设计正交表L(3)。

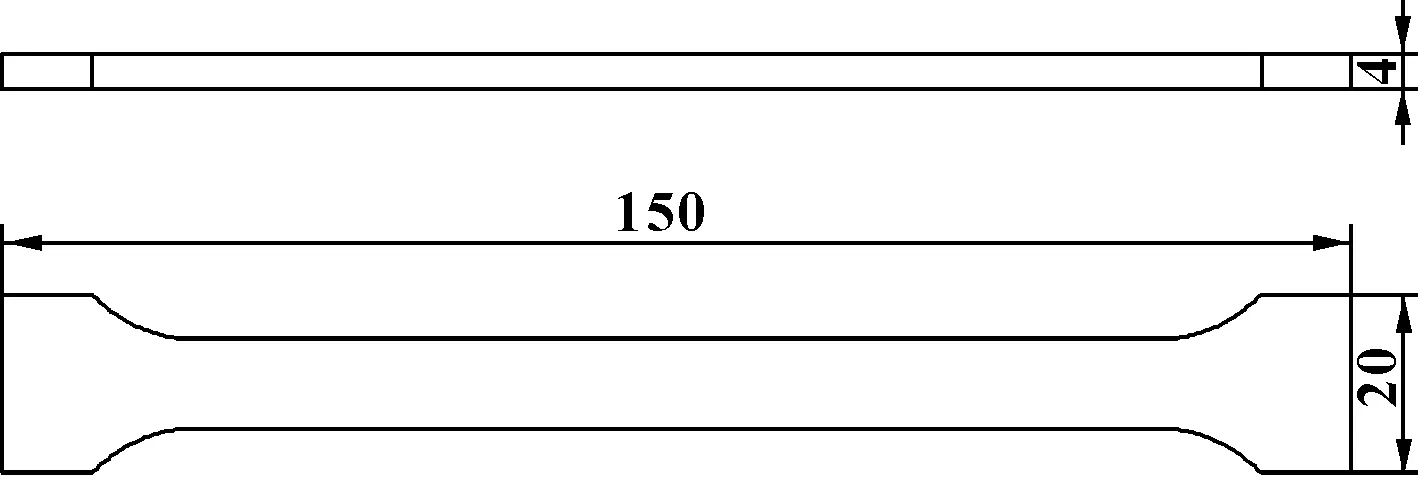
图1 标准测试样件尺寸

表1 正交试验因素水平

每组试验同时烧结6个标准测试样件，如图2所示。试验结束后利用数显游标卡尺测量每组6个标准测试样件x、y、z方向的尺寸，将每组相对误差先取绝对值再求取加权平均值，计算成形件各方向上的收缩率，定义如下：

图2 试验模型实物

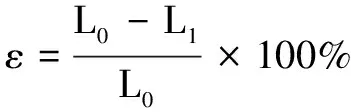
(1)

式中：ε为收缩率；L表示设计尺寸；L为制件实际尺寸。

1.2 多目标函数统一化

由于工艺参数组合的选取是一个多目标优化问题，在多目标优化技术中，一般很难使分目标同时达到最优。因此，本文作者利用线性加权组合法将各项转化为统一目标函数，消除量纲并确定各项加权因子。

已知各项目标函数值的区间范围：

α≤f(x)≤βj=1,2,3,…,t

(2)

则：

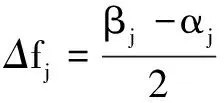
(3)

f为各目标函数容限，加权因子取：

(4)

针对选择性激光烧结工艺参数的优化，将其试验结果的向收缩率、向收缩率、向收缩率作为各项目标函数进行转化，得到成形件统一性能的函数为

=0.216+0.248+1.150

(5)

将、以及代入公式(5)中，可以计算出统一目标函数值，如表2所示。可知：统一性能的数值越小，成形件精度越高。

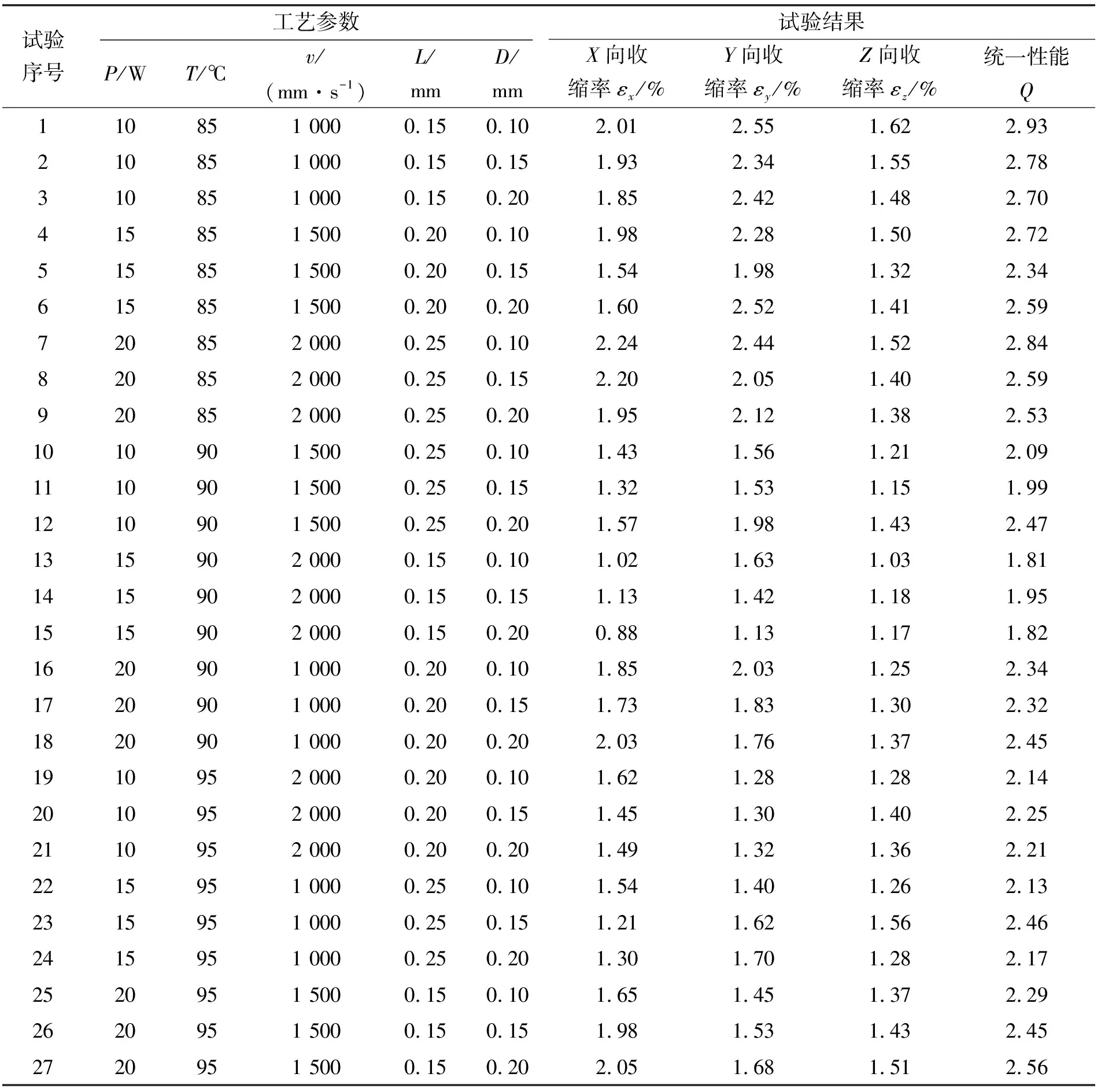
表2 工艺参数及试验结果

2 基于SOA-LSSVM的精度预测模型

2.1 LSSVM预测模型

最小二乘支持向量机是由SUYKENS等在支持向量机(SVM)基础上提出的新型回归算法,LSSVM具有传统SVM解决小样本非线性不可分问题的优点。假设训练样本数据为{(，),(=1,2,…,)}，其中:∈为输入变量,包括：激光功率、预热温度、扫描速度、扫描间距和分层厚度，=5;∈为对应的输出值，高维非线性映射:→，为高维特征向量，此时特征向量空间拟合样本集为

=()+

(6)

式中：为权向量；为偏置量。

为解决SVM中的二次规划问题，基于正则化理论，采用最小二乘法建立LSSVM的最小化优化函数，其表达式为

(7)

s.t.=()++

(8)

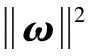
建立最小化函数的拉格朗日求解方程：

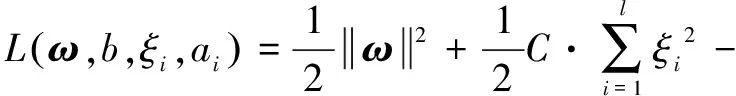
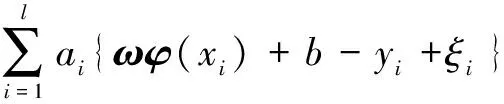
(9)

式中：为拉格朗日乘子，=1,2,…,,≥0。

分别求取对、、、的偏导数，并令其为0：

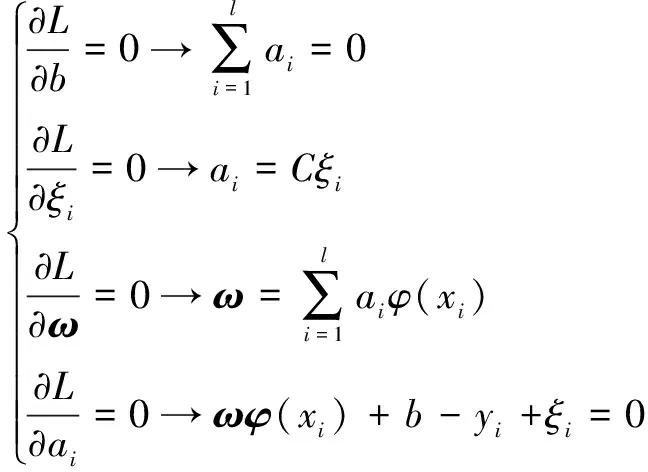
(10)

化简式(10)中的和可得：

(11)

式中：为阶单位矩阵；=[1,…,]；=[,,…,]；=[,,…,]；=(,)。

由于RBF核函数需要预设的参数较少，采用RBF函数作为LSSVM模型的核函数，即：

(12)

式中：为核函数参数。

LSSVM最终优化模型为

(13)

2.2 人群搜索算法

LSSVM模型预测精度取决于核函数参数和惩罚系数的取值。为提高预测精度，采用人群搜索算法对其参数进行优化。人群搜索算法是一种基于种群的新型启发式随机搜索算法。在该算法中，通过评估对应位置变化的响应，根据经验梯度来选择搜索方向，并基于模糊规则的不确定性推理决定步长。人群搜索算法具有概念明确、易于理解、收敛速度快和精度高等特点。

2.2.1 搜索步长的确定

SOA算法在确定步长时先将个体最佳适度值按递减的顺序排列，并将个体赋予从1到(为种群大小)的顺序编号作为模糊推理的输入，采用高斯隶属度函数表示搜索步长的模糊变量，如式(14)所示：

()=e[-(-)](2)

(14)

式中：为高斯隶属度；为输入变量；、均为隶属函数参数。设定最小隶属度=0.011 1，最大隶属度=0.950 0。

其他位置隶属度可由式(15)和式(16)表示：

(15)

=(,1)

(16)

式中：为第个个体对应的隶属度；()为第个个体最佳适应度值按降序排列后的顺序编号；为种群规模，=30；为维搜索空间的目标函数值对应的隶属度，函数(,1)产生均匀随机分布在[,1]上的实数。

搜索步长由公式(17)确定：

(17)

式中：为维搜索空间的搜索步长；为高斯隶属函数的参数，其值可以由下列公式确定：

=()|-10(1,3)|

(18)

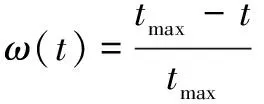
(19)

式中：表示全局最优；(1,3)表示产生均匀随机分布在[1,3]上的实数；()为第次迭代的权重函数值，随迭代次数的增加从0.9线性递减至0.1;为当前迭代次数；为最大迭代次数，=100。

2.2.2 搜索方向的确定

在确定搜索步长后，将第个个体与个体最佳和全局最佳进行比较确定搜索方向是利己方向,ego、利他方向,alt还是预动方向,pro，如下式所示：

,ego()=,best-()

(20)

,alt()=,best-()

(21)

,pro()=()-()

(22)

式中：,best表示第个搜寻个体所在领域的群体历史最优位置；,best表示第个搜寻个体经过的最优位置；()为个体当前位置。

采用3个方向的随机加权几何平均数为标准确定搜索方向，计算公式如下所示：

()=sign(ω,pro+,ego+,alt)

(23)

(24)

式中：为惯性权值；和为常数，取值范围为[0,1]；为当前迭代次数，取值为[2,]内的整数；权重最大值=0.9，权重最小值=0.1。

2.2.3 个体位置的更新

确定搜索步长和方向后，要对个体位置进行更新。位置更新公式如下：

Δ(+1)=()()

(25)

(+1)=Δ(+1)+()

(26)

2.3 SOA-LSSVM精度预测模型建立

采用LSSVM建立激光烧结工艺参数组合与统一性能之间的非线性映射关系，在该模型中,假设有组训练样本数据(，)(=1,2,…,)，其中为五维实数输入向量，分别包括激光功率、预热温度、扫描速度、扫描间距、分层厚度，以统一性能作为选择性激光烧结成形件精度评价指标即输出。

针对需要优化的参数=[](=1,2,…,30)，根据预测样本的均方根误差(Root Mean Square Error，RMSE)构建适应度函数：

(27)

人群搜索算法优化LSSVM的主要步骤：

(1)数据预处理。将数据样本分为训练样本和测试样本，从不同预热温度水平中抽取第4、16、24水平的数据作为测试集，其余24组数据为训练集，采用Min-Max标准化方法将数据映射到[0,1]。归一化公式如下：

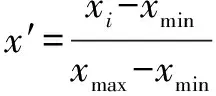
(28)

式中：′为归一化后的数据；为样本数据；为样本数据的最小值；为样本数据最大值。

(2)设定SOA基本参数，初始化种群规模、种群个体、迭代次数、最大和最小隶属度以及权值的最大值和最小值。

(3)利用SOA对LSSVM的参数进行寻优，将训练样本输入LSSVM模型中进行学习，得到精度预测值并计算适应度。

(4)根据适应度函数找出参数和的个体最优和全局最优位置，并更新参数和的位置，直到迭代满足终止条件=100或适应度最小，然后输出；否则返回。

(5)将预测样本代入训练好的LSSVM模型进行预测，预测完成后，对预测结果进行反归一化。反归一化公式为

=′(-)+

(29)

3 模型预测结果与分析

SOA-LSSVM预测模型的初始化参数如下：种群规模=30;最大迭代次数为100；最大隶属度=0.950 0，最小隶属度=0.011 1；权重最大值=0.9，权重最小值=0.1。采用MATLAB R2017a建立SOA-LSSVM的预测模型，抽取第4、16、24水平的数据作为测试集。其余24组数据为训练集。图3所示为参数寻优过程中的适应度曲线，反复验证最终选取优化参数为=14.68，=1.657。

图3 SOA-LSSVM预测模型适应度曲线

为验证SOA-LSSVM精度预测模型的优劣，分别采用BP 神经网络、LSSVM模型以及SOA算法优化后的LSSVM对同一样本数据进行统一性能预测和相对误差对比，结果分别如图4—图6所示。预测结果表明：3种模型的期望输出结果都符合真实值的变化趋势，但预测值和真实值之间总存在一定误差，本文作者提出的SOA-LSSVM模型预测曲线更接近统一性能真实值变化曲线。

图4 BP神经网络与LSSVM模型预测结果图5 SOA-LSSVM模型预测结果

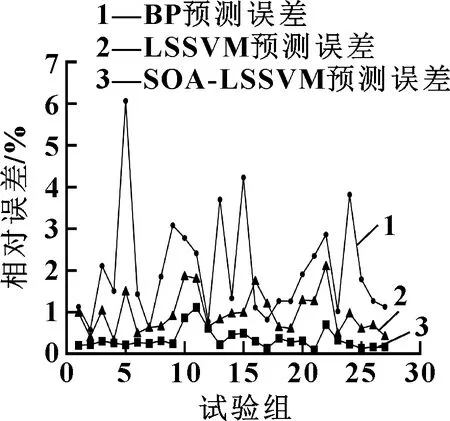
图6 预测误差对比

引入平均绝对误差(Mean Absolute Error，MAE)和均方根误差作为检验标准，两者计算值越小，说明模型的预测精度越好，结果如表3所示。可以看出：SOA-LSSVM预测模型相较于BP神经网络以及LSSVM模型，其MAE和RMSE都较小；BP神经网络最大相对误差达到6.07%，最小相对误差达到0.58%；LSSVM模型最大相对误差达到2.11%，最小相对误差达到0.33%；文中采用的SOA-LSSVM模型最大相对误差仅为1.11%，最小相对误差达到0.09%。因此，利用SOA算法优化的LSSVM模型针对小样本预测问题具有良好的泛化能力，可以用于激光烧结工艺参数组合优化。