基于改进模糊聚类和最大信息系数的数控机床温度测点选取

2022-09-16叶天玺娄平严俊伟胡建民

机床与液压 2022年6期

叶天玺，娄平，严俊伟，胡建民

(1.武汉理工大学信息工程学院，湖北武汉 430000；2.湖北经济学院信息与通信工程学院，湖北武汉 430205)

0 前言

重型机床加工过程中，热误差是影响加工结果的关键因素。研究表明，热误差占机床加工过程总误差的40%～70%。热误差补偿法被认为是消除热误差的最有效方法，而温度测点的选取是建立热误差模型的基础。国内外学者对温度测点选取进行了深入研究，并提出许多方法选取合适的温度测点，如模糊聚类、模糊聚类与灰色关联分析、灰色关联分析、线性相关分析、有限元分析等。但上述方法优化过程过于简单，选取的测点并不准确，进而导致热误差模型精度降低。本文作者利用改进模糊聚类对温度测点进行分组，然后通过MIC(Maximal Information Coefficient)确定每组内与热误差值最相关的关键温度测点，将128个测点降至4个关键温度测点，通过BP神经网络建立热误差模型，用重型机床的热误差实验测量数据对热误差模型进行验证。

1 关键温度测点选取方法

选择合适的关键温度测点将直接提高热误差模型的预测精度。YANG于2012年根据元启发算法提出花朵授粉算法(Flower Pollination Algorithm,FPA)。本文作者利用模糊C均值(Fuzzy C-means，FCM)算法提出如图1所示的选取温度测点的流程。在获得温度数据和热误差数据后，对数据进行预处理；使用聚类方法对128个温度测点分类，以避免多温度测点间存在复共线问题；通过相关分析，进一步选取关键温度测点，提取每组中与热误差最相关的温度测点。

图1 优化温度测量点流程

1.1 改进模糊聚类算法

(1)

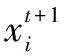
自花授粉迭代公式为

(2)

采用具有全局优化能力的FPA算法计算FCM的初始温度聚类中心；根据公式(3)和公式(4)分别更新温度隶属度矩阵和温度聚类中心，直到满足迭代条件。

(3)

(4)

其中：是温度聚类中心和温度向量的隶属度矩阵；是模糊权重指数，通常=2。FPA-FCM算法流程如图2所示。

图2 FPA-FCM算法流程

1.2 最大信息系数

RESHEF等在2011年提出最大信息系数(MIC)。该方法基于信息论对温度测点和热误差数据的相关性进行度量，通过网格划分与互信息计算MIC值。利用温度测点和热误差数据的数据集，可以获得--网格的分区。在这种情况下，相互信息定义为

(5)

其中:(,)是联合密度函数;()、()是边缘概率分布函数。假设网格G中所有像元中的(，，)的最大值为(,,)，为便于比较不同尺寸，将(,,)进行归一化：

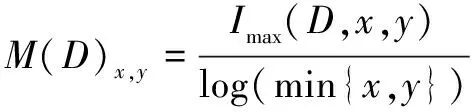
(6)

令样本大小为、最大网格划分数为()，则数据集的MIC定义为

MIC(),=max,<(){(),}

(7)

通常()的值设为。MIC值在0～1之间，值越大，温度测点和热误差数据的相关性越高。

2 实验与验证

2.1 温度测点分类

将ZK5540A重型数控机床用作温度场监控测试台，124个温度传感器部署在机床表面，具体分布如图3所示。出于安全考虑，主轴转速设定为500～2 000 r/min。

图3 机床表面的温度传感器分布

为探究环境温度对机床热误差的影响，添加4个环境温度传感器在机器周围进行实时监控。由于该实验中，在、方向上机床的热误差相比方向热误差数据可以忽略不记，在研究机床的热误差时，主要考虑主轴在方向上的热漂移。如图4所示，在3个方向上使用分辨率为0.1 μm、采样频率为300 kHz的Keyence LK-G5000高速激光位移传感器采集热误差数据。

图4 高速激光位移传感器

利用FPA-FCM算法对温度测点进行聚类，并通过Dunn指数和迭代次数对算法的聚类效果和收敛速度进行评估。Dunn指数越大，则证明聚类效果越好。通过FCM聚类，当迭代次数达到100时，Dunn值达到0.003 947(见图5)。随着迭代次数增加，Dunn值仍会出现波动，这说明使用FCM易陷入局部最优解。而当FPA-FCM的迭代次数为10时，Dunn指数可以直接达到0.181 622，之后多次实验也不会出现波动(见图6)。这证明了与FCM相比，FPA-FCM不仅减少了迭代次数，还防止了在聚类过程中陷入局部最优解。

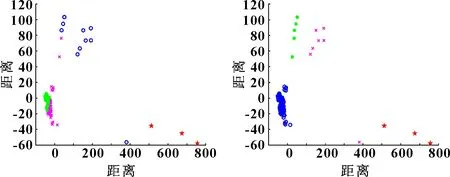
图5 DI=0.003 947,迭代100次图6 DI=0.181 622,迭代10次

2.2 关键温度测点选取

文中共进行6组实验，数据集为变转速工况下热误差数据和温度数据。其中第1组和第2组训练集是当月三日的温度数据，而测试集为当月单日温度数据。第3组和第4组训练集选取当月的四天温度数据，而测试集则选取其他月份的单日温度数据。第5、6组是不同月份训练集的五天温度数据，而测试集是随机单日温度数据。

对每组实验数据进行分类后，需要进行相关分析。通过相关分析，能够确定每种类型的数据中与热误差最相关的关键温度测点。在此实验中，用FF-MIC(FPA-FCM-MIC)、F-Grey(FCM-Grey correlation)、F-Pearson(FCM-Pearson)、Grey correlation、Pearson等方法选取关键温度测点，具体如表1所示。

表1 关键温度测量点的选择

2.3 热误差建模

为验证5种优化测点方法的有效性，建立基于BP神经网络的热数据模型。BP神经网络的结构由输入层、隐藏层、输出层组成。输入节点数为已确定的关键温度测点数，输出为热误差预测值，因此输出节点为1。建立输入节点数为4、输出节点数为1、单层隐藏层节点数为60的网络结构。BP神经网络其他参数设置：隐藏层函数设为relu，loss函数设为MSE，优化器选择ADAM，学习速率设为0.000 1，最大迭代次数为2 000。