基于ADAMS的行星轮系均载特性研究
2022-09-16董书洲秦训鹏丁锐丁吉祥
董书洲,秦训鹏,丁锐,丁吉祥
(武汉理工大学汽车工程学院,湖北武汉 430070)
0 前言
NGW型行星轮系具有结构紧凑、体积小、质量轻、传动比大等优点,被广泛应用于电动车的轮毂减速器中。但在实际工作过程中,行星轮之间的载荷分配不均,易导致减速器系统产生振动与噪声,影响减速器系统的性能。为提高行星传动系统均载性能,国内外学者对此进行了大量的研究。KAHRAMAN等对行星传动系统静力学均载特性做了较为全面的研究。尚珍等人研究了行星轮偏心误差、浮动结构、行星轮个数和齿侧间隙对行星轮系均载性能的影响。陆俊华等分析了各构件的制造和安装误差对行星传动系统动态均载特性的影响。董皓等人研究了行星轮个数及间隙对行星传动系统均载特性的影响。朱增宝等研究了支撑刚度对行星传动系统动态均载特性的影响及建立采用中心浮动件的封闭差动人字齿轮传动系统动力学模型,分析了各构件制造和安装误差对行星传动系统均载特性的影响。巫世晶等以复合轮系为研究对象,建立中心轮浮动的非线性动力学模型,分析了啮合误差对行星传动系统动态均载特性的影响。周金阳等分析了封闭行星轮系振动位移响应及输入转速、输入功率和摩擦因数对均载特性的影响。SANCHEZ-ESPIGA等研究了啮合相位和各种误差对行星传动系统均载性能的影响。LIU等研究了太阳轮浮动结构对行星传动系统的振动响应以及动力学参数的影响。
大多数学者通过建立行星轮系动力学方程,运用数值求解的方法研究时变刚度、制造和安装误差、支撑刚度、齿侧间隙等因素对系统均载特性的影响。本文作者建立了考虑齿面摩擦的动力学模型,并通过动力学仿真的方法分析了有无齿面摩擦情况下浮动结构以及输入转速、载荷、摩擦因数对系统均载特性的影响。
1 动力学模型
轮毂减速器由输入轴、太阳轮、行星轮、行星架、内齿圈以及输出轴组成,传动简图如图1所示。
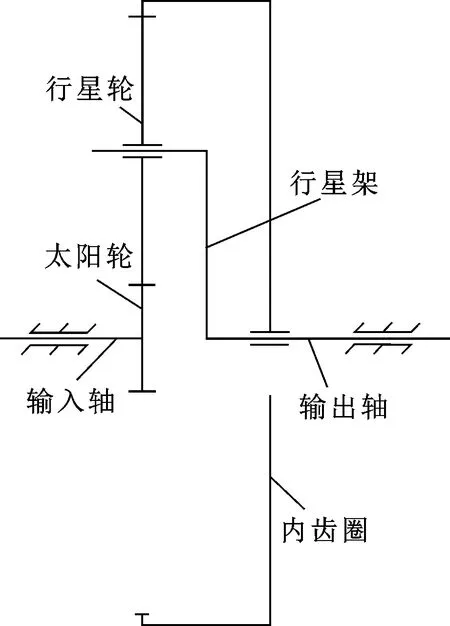
图1 减速器传动简图
以行星架回转中心为坐标原点,建立随行星架转动的动坐标系,忽略太阳轮、内齿圈的支撑阻尼,各转动构件的旋转刚度和旋转阻尼以及行星轮的中心浮动位移。太阳轮以及内齿圈的支承刚度等效为弹簧,太阳轮与行星轮、内齿圈与行星轮之间的接触等效为弹簧阻尼系统。齿面之间的摩擦简化为库仑摩擦。采用集中质量法建立的系统动力学模型如图2所示。不考虑构件的轴向移动,此行星轮系共有10个自由度,包括太阳轮角位移,行星轮角位移p(=1,2,3),行星架角位移,内齿圈角位移,太阳轮和内齿圈沿水平和竖直方向上的中心浮动位移、和、。
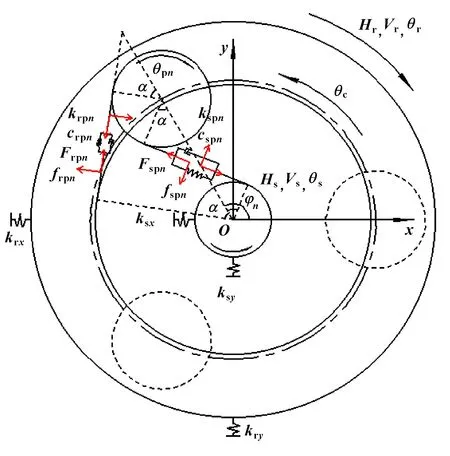
图2 动力学模型
其中:s、s和r、r分别为太阳轮和内齿圈沿水平、竖直方向上的支承刚度;sp、rp和sp、rp分别为第个行星轮与太阳轮、内齿圈的啮合刚度和啮合阻尼;sp、rp分别为第个行星轮与太阳轮、内齿圈的啮合力;sp、rp分别为第个行星轮与太阳轮、内齿圈之间的摩擦力。
2 数学模型
2.1 啮合力
太阳轮、内齿圈与第个行星轮之间的啮合力为
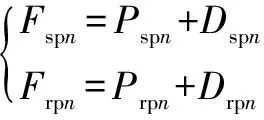
(1)
上述方程的建立以及参数具体含义在文献[3]中有详细说明。
2.2 摩擦力及摩擦力臂
根据库仑摩擦定律,行星轮与太阳轮、内齿圈之间的摩擦力为
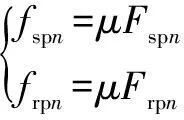
(2)
式中:为齿面滑动摩擦因数。
当齿轮啮合重合度大于1时,存在多对轮齿同时啮合的情况。定义行星轮第(=1,2,…,)对轮齿从进入啮合区域开始经过时间移动的距离为
=[mod(,)+(-1)]
(3)
式中:为行星轮在动坐标系中的角速度;为行星轮基圆半径;为行星轮与太阳轮、内齿圈的啮合周期,=60/;mod()为取余函数。
太阳轮与行星轮之间作用的摩擦力对太阳轮、行星轮的摩擦力臂(如图3所示)分别为
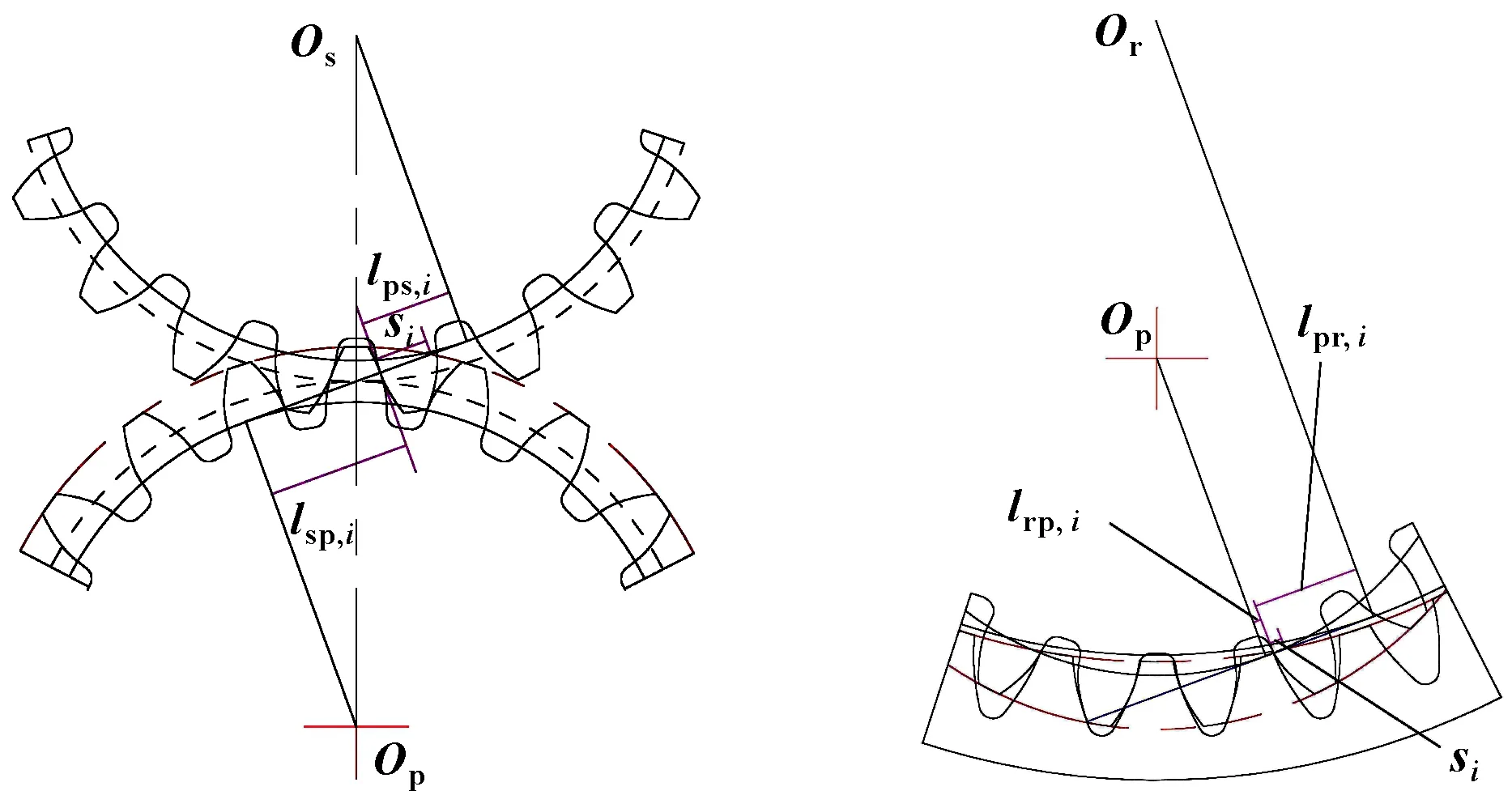
图3 太阳轮与行星轮的摩擦力臂示意 图4 内齿圈与行星轮的摩擦力臂示意
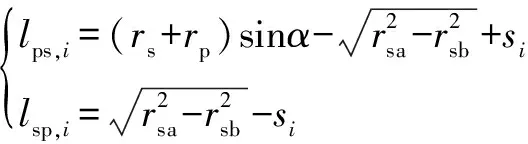
(4)
式中:sp,、ps,分别为太阳轮与行星轮之间的摩擦力对行星轮、太阳轮的力臂大小;、分别为太阳轮和行星轮分度圆半径;、分别为太阳轮齿顶圆半径和基圆半径;为压力角。
行星轮与内齿圈之间作用的摩擦力对行星轮、内齿圈的摩擦力臂(如图4所示)分别为
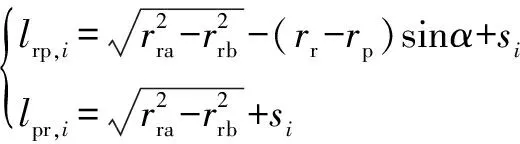
(5)
式中:rp,、pr,分别为内齿圈与行星轮之间的摩擦力对行星轮、内齿圈的力臂大小;为内齿圈分度圆半径;、分别为内齿圈齿顶圆半径和基圆半径。
2.3 微分方程
根据牛顿第二定律推导出系统运动微分方程。
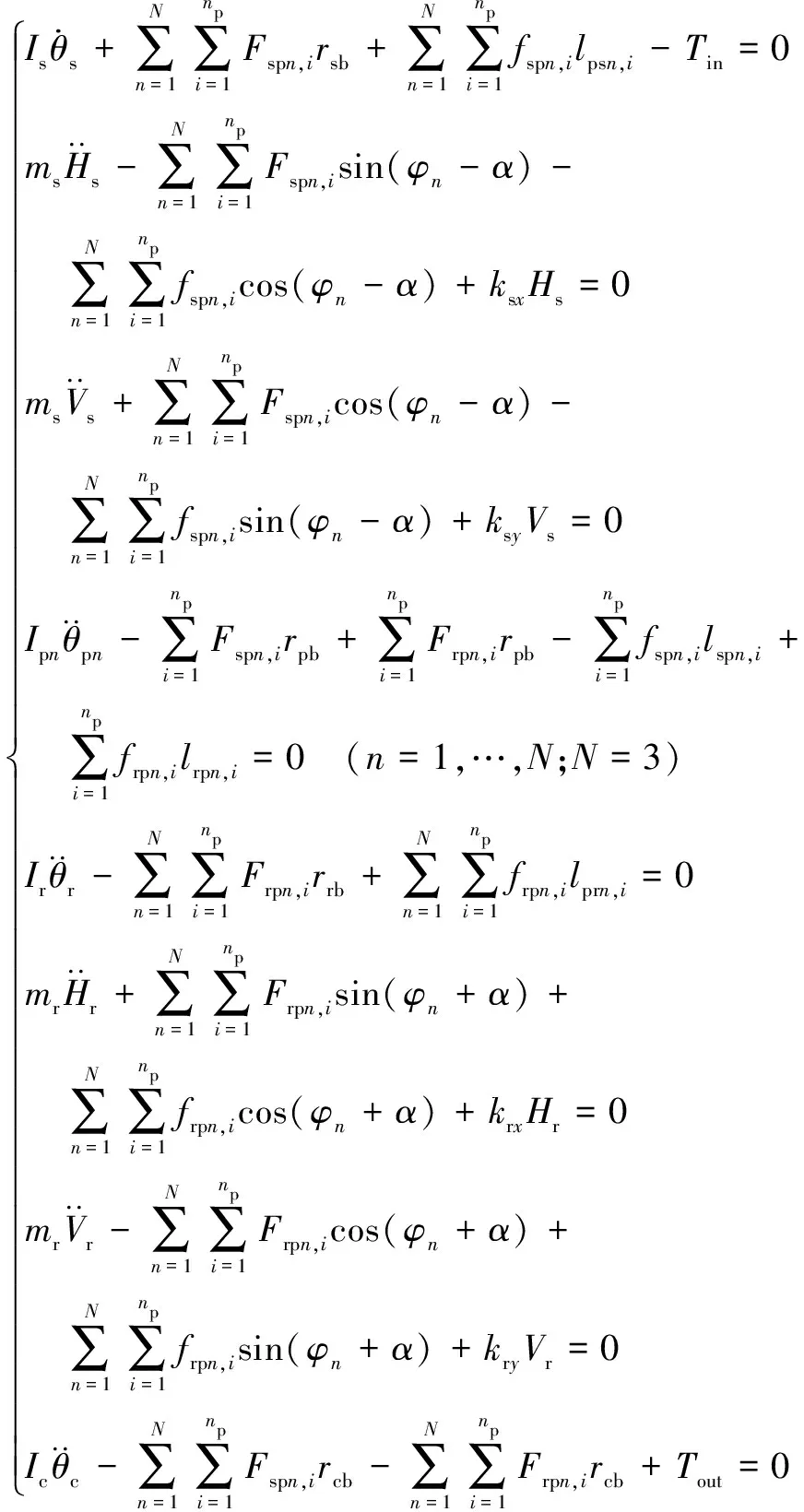
(6)
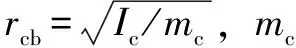
2.4 定义均载系数
太阳轮、内齿圈与行星轮之间的均载系数定义以及参数说明在文献[12]中有详细说明。
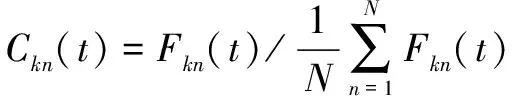
(7)
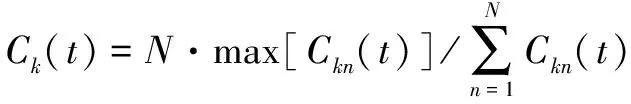
(8)
=max[()]
(9)
式中:()为瞬时动载系数;()为瞬时均载系数;为均载系数。
3 动力学仿真分析
3.1 模型及参数
在UG中建立的三维模型如图5所示,行星轮系各齿轮的参数如表1所示。

图5 三维模型

表1 行星轮系各齿轮参数
3.2 仿真设置
行星架与地面、行星轮与行星架之间设置转动副。无浮动结构,太阳轮与地面之间设置转动副,内齿圈与地面之间设置固定副。单浮动结构,太阳轮与地面设置轴套副,内齿圈与地面设置固定副。双浮动结构,太阳轮、内齿圈与地面分别设置轴套副。太阳轮与地面之间的轴套副不能限制太阳轮的转动,绕其轴线旋转刚度设置为0。内齿圈与地面之间的轴套副要限制内齿圈的转动,绕轴线旋转刚度设置为2×10N·mm/(°)。
根据Hertz碰撞理论,计算得到行星轮与太阳轮、行星轮与内齿圈之间的接触刚度分别为5.4×10、7.9×10N/mm;金属接触力指数取1.5;阻尼值为刚度大小的1‰;接触深度为0.1 mm。
齿轮材料选取20CrMnTi,根据文献[14]中的公式(10)计算20CrMnTi材料接触的静、动摩擦因数。20CrMnTi的弹性模量=2.1×10N/mm,屈服应力=850 N/mm。经计算=0.128,=0.09。研究浮动结构对行星轮系均载性能影响以及行星轮系均载特性时不考虑润滑油的润滑作用。
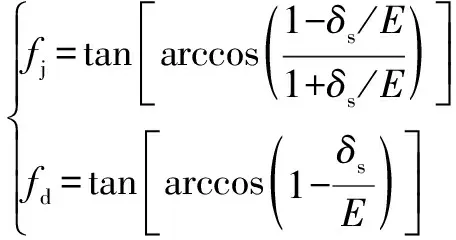
(10)
3.3 仿真计算
采用step函数使输入转速在0~1 s从0增加到1 800 r/min,在1~3 s内稳定在1 800 r/min。行星架施加负载转矩为5×10N·mm。
3.3.1 传动比与啮合力验证
根据仿真结果得到不同状态下的传动比以及与理论传动比之间的误差如表2所示。
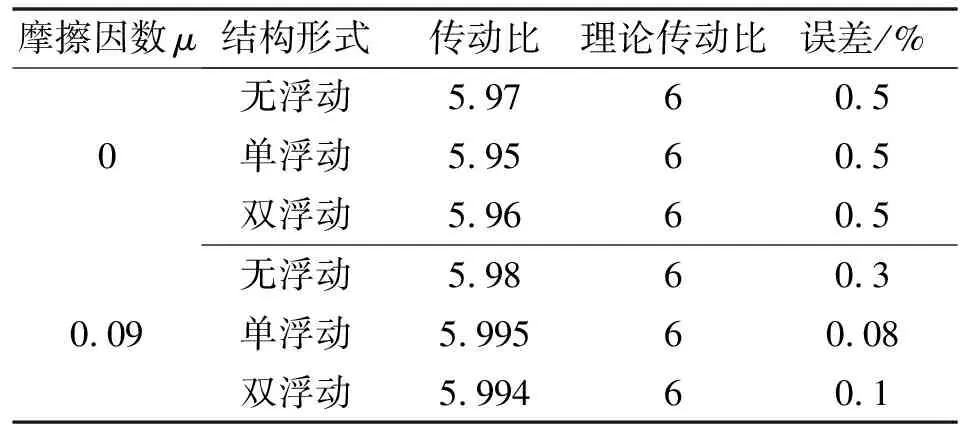
表2 不同状态下的传动比及误差
=0时计算太阳轮与行星轮之间的理论啮合力时机械效率=1,=0.09时计算太阳轮与行星轮之间的理论啮合力时机械效率=0.98。根据仿真结果计算得到不同状态下太阳轮与行星轮之间的平均啮合力及与理论啮合力之间的误差如表3所示。
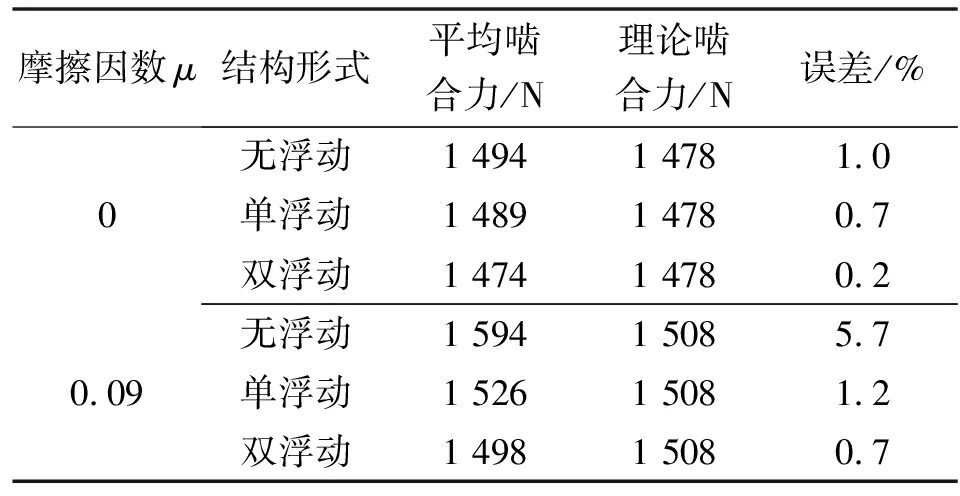
表3 不同状态下的平均啮合力及误差
由表2和表3可知不同状态下仿真得到的传动比与理论传动比误差均在1%内,平均啮合力与理论啮合力的误差均在6%内,仿真结果能够反映行星轮系的实际工作状况。
3.3.2 仿真结果与分析
=0时无浮动结构、单浮动结构、双浮动结构太阳轮、内齿圈与行星轮之间的啮合力如图6—图8所示。=0.09时太阳轮、内齿圈与行星轮之间的啮合力与=0时无明显差异,故=0.09时的啮合力变化图不再赘述。
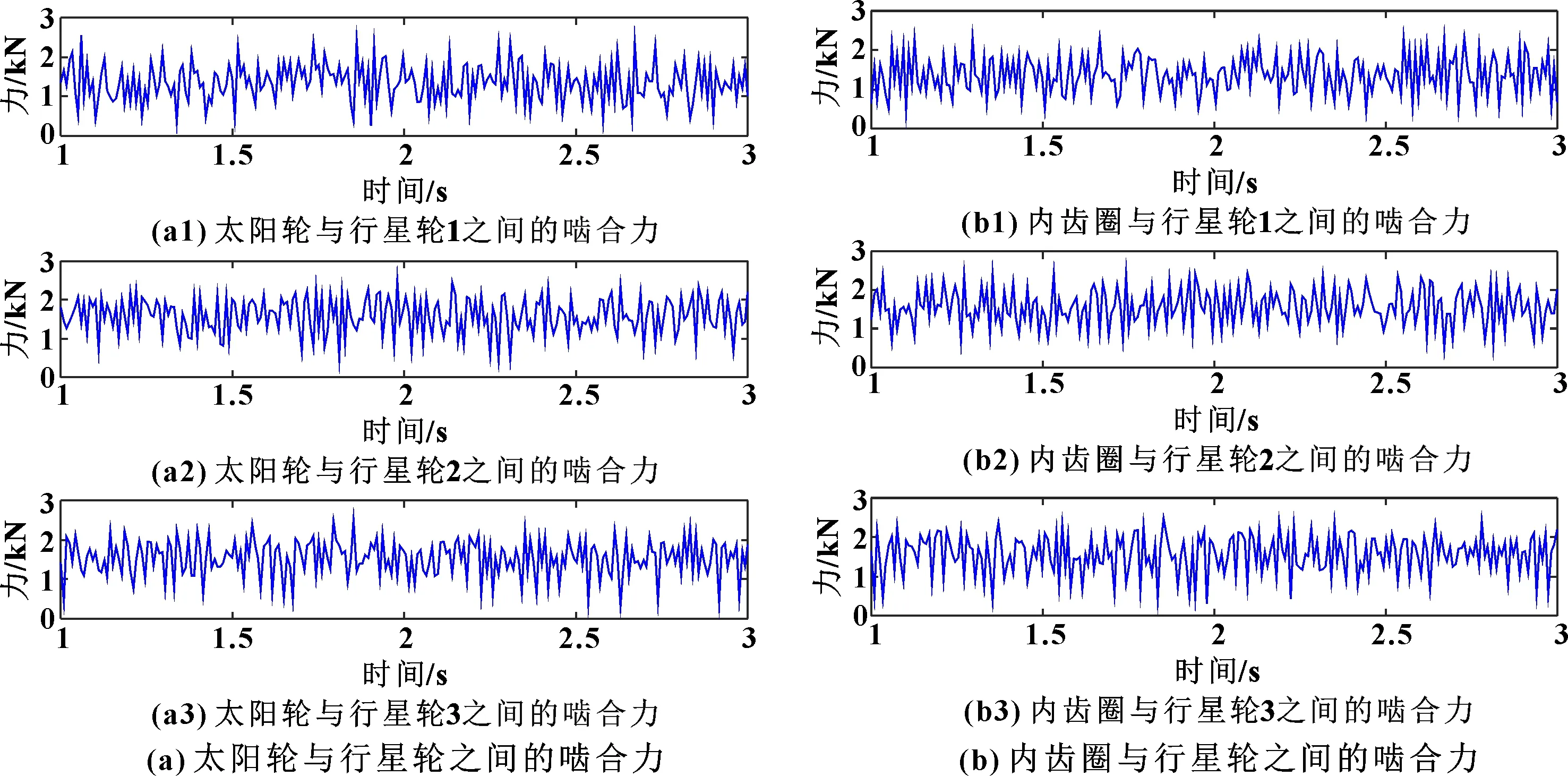
图6 无浮动结构
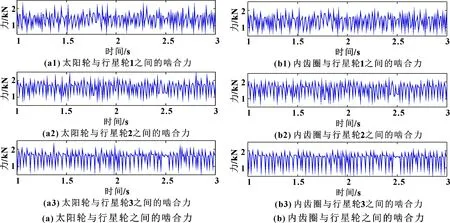
图7 单浮动结构
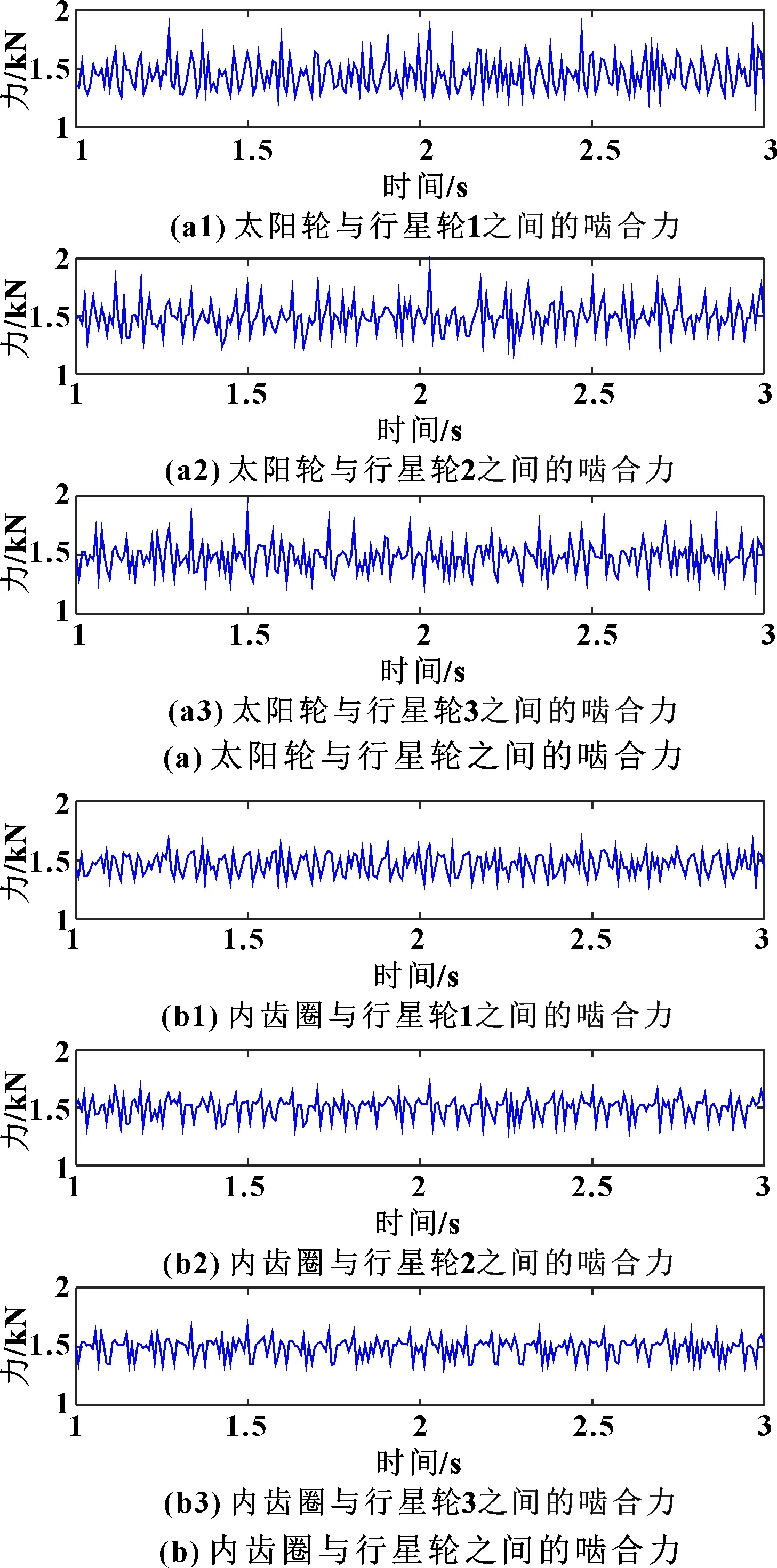
图8 双浮动结构
由图6—图8可知:3种浮动结构太阳轮与行星轮之间的啮合力均具有周期性,单浮动、双浮动结构的啮合力变化相比于无浮动结构更为均匀,与此同时,双浮动结构的啮合力相对于单浮动结构变化更为均匀。根据均载系数的定义,可以定性地判断双浮动结构的均载性能要优于其他两种结构。其原因在于双浮动结构的太阳轮不仅和单浮动结构一样在径向存在调整间隙,使用双齿联轴器的内齿圈在轴向和径向也存在调整间隙。
由啮合力仿真结果及公式(7)—(9)得到不同状态下的均载系数如表4所示。
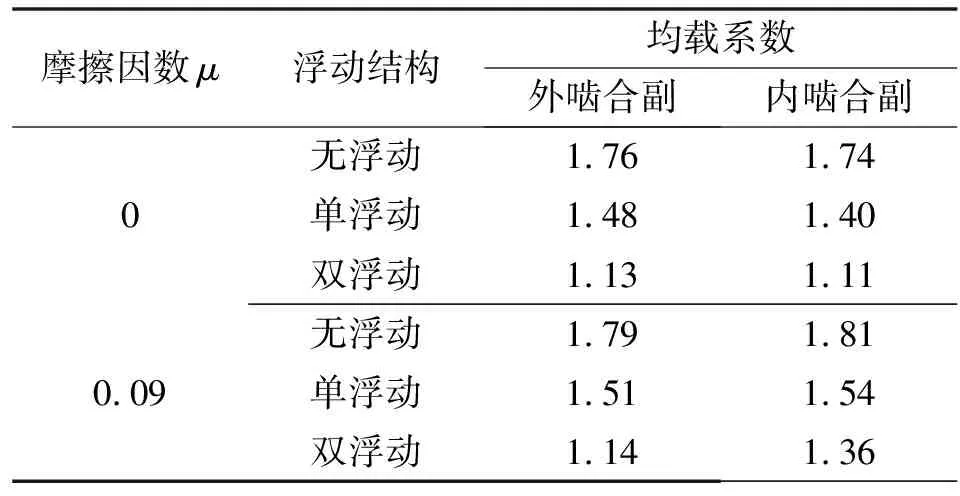
表4 不同状态下均载系数
不论有无齿面摩擦,无浮动、单浮动、双浮动结构下太阳轮、内齿圈与行星轮之间的均载系数均依次减小,可以定量地说明双浮动结构均载性能优于单浮动结构、单浮动结构均载性能优于无浮动结构。
3.4 均载特性
轮毂减速器实际联接方式采用的是双浮动结构,电机的输出端与行星轮系的输入端、行星轮系的输出端与轮毂输入端均采用含有间隙的花键联接。以双浮动结构轮毂减速器为对象研究其均载特性。
研究转速对行星轮系均载性能的影响时,输入转速为500~5 000 r/min,行星架负载转矩为200 N·m,滑动摩擦因数为0.09。通过仿真得到输入转速对内外啮合副均载系数的影响如图9所示。可知:随着转速的增加,行星轮系内外啮合副的均载系数均在增加;转速较小时,随着转速的增加,内外啮合副均载系数变化趋势相差不大;当转速增加到一定程度时,外啮合副均载系数的增长趋势比内啮合副更加明显;当转速过大时,系统的均载特性显著变差。
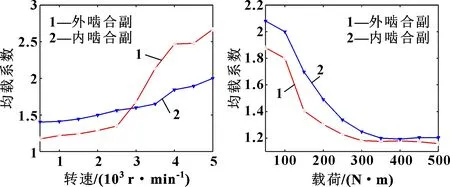
图9 输入转速对内外啮合副均载系数的影响 图10 载荷对内外啮合副均载系数的影响
研究载荷对行星轮系均载性能的影响时,载荷为50~500 N·m,输入转速为1 800 r/min,滑动摩擦因数为0.09。通过仿真得到载荷对内外啮合副均载系数的影响如图10所示。可知:随着载荷的增加,行星轮系内外啮合副的均载系数均在减小;载荷较小时,随着载荷的增加,内、外啮合副均载系数下降趋势比较明显;当载荷增加到一定程度后,内、外啮合副的均载系数随着载荷的增加变化趋势逐渐趋于平缓。
研究摩擦因数对行星轮系均载性能的影响时,摩擦因数为0~0.1,输入转速为1 800 r/min,行星架负载转矩为200 N·m,通过仿真得到摩擦因数对内外啮合副均载系数的影响如图11所示。可知:随着摩擦因数的增加,行星轮系内、外啮合副均载系数只有小幅度变化,故摩擦因数对行星轮系均载性能的影响较小。此外,考虑齿面摩擦时内、外啮合副的均载系数均大于无齿面摩擦的情况。
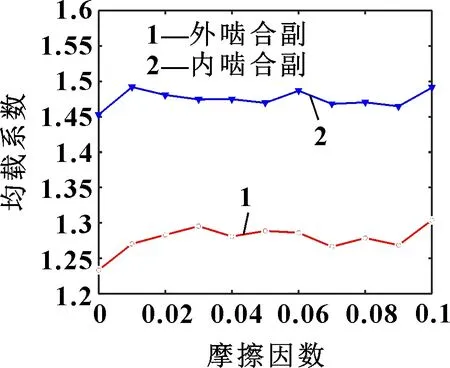
图11 摩擦因数对内、外啮合副均载系数的影响
4 结论
以轮毂减速器中的NGW型行星轮系为研究对象,建立考虑齿面摩擦十自由度动力学模型,并推导了动力学微分方程。利用ADAMS对行星轮系进行动力学仿真,得出以下关于均载特性结论:
(1)不论有无齿面摩擦,双浮动结构的均载性能优于单浮动结构和无浮动结构。
(2)系统均载系数随着转速的增加而增加。当转速过大时,系统均载特性显著变差。
(3)系统均载系数随着载荷的增加而减小,载荷增加至一定程度时,均载系数变化趋势趋于平缓。
(4)系统均载系数随着摩擦因数的增加而小幅度变化,摩擦因数对系统均载特性影响较小,且考虑齿面摩擦时内、外啮合副的均载系数均大于无齿面摩擦的情况。
