基于虚拟堆积试验的食用玫瑰花瓣离散元参数标定

勾富强 尹志宏 牛宪伟 严跃拨

(1. 昆明理工大学机电工程学院，云南 昆明 650500；2. 腾翎机械科技〔云南〕有限公司，云南 昆明 650500)

目前对食用玫瑰花瓣的研究，主要集中于玫瑰花瓣的干燥、成分分析、食品工艺研究等方面。而对于食用玫瑰花瓣的加工设备的研制，方卫山等[1]研制的食用玫瑰花瓣的初分选成套设备进一步推动了玫瑰花瓣的加工水平。为提高食用玫瑰花瓣的加工设备研制速度，研究食用玫瑰花瓣与加工设备之间的相互作用，食用玫瑰花瓣的建模与参数标定显得尤为重要。

离散单元法是一种研究物料散体运动行为的数值模拟方法，能够较为直观地研究物料的非线性运动姿态[2]。对于难以通过物理试验直接获取的参数，通常采用堆积角试验、直剪切试验和压缩试验的参数标定方法。马彦华等[3]通过物理试验和仿真相结合的方法，标定了苜蓿秸秆的仿真参数；廖宜涛等[4]通过油菜茎秆弯曲破坏仿真试验进行了仿真参数标定；侯杰等[5]基于堆积试验标定了水稻茎秆接触参数。基于上述文献，结合食用玫瑰花瓣结构特征，研究提出采用离散元方法建立柔性食用玫瑰花瓣离散元模型，通过物理堆积试验与虚拟堆积试验相结合，采用Placket-Burman试验、最陡爬坡试验和Box-Behnken试验确定对堆积角影响显著的因素以及参数取值，以期为食用玫瑰花瓣离散元仿真研究提供数据支持。

1 食用玫瑰花瓣柔性离散元建模

食用玫瑰花瓣属于散粒体物料，基于GB/T 4472—2011中关于固体密度的测量方法，测量得到食用玫瑰花瓣的真实密度均值为552.8 kg/m3。基于JB/T 9014.7—1999标准，将200 g的食用玫瑰花瓣装入内径为100 mm，高200 mm的不锈钢空心圆筒进行匀速提升，形成锥形堆积体，测量堆积体母线与水平线的夹角，得到食用玫瑰花瓣的堆积角约为26°。

1.1 食用玫瑰花瓣模型多球面位置信息获取

食用玫瑰花瓣离散元模型采用多球面颗粒组合[6]，每个球面之间采用Bond黏结键进行黏接，模拟出与真实花瓣相类似的模型。由于食用玫瑰花瓣的结构属于空间曲面结构，采用手动填充的方法较为繁琐。采用基于颗粒填充法建立食用玫瑰花瓣模型[7]，能够快速准确获取多球面位置信息。假设食用玫瑰花瓣的平均厚度为1 mm，在SolidWorks 2018中建立食用玫瑰花瓣的三维模型，并导入EDEM 2020中，添加球形颗粒填充材料，球面半径为0.5 mm。颗粒填充后，得到如图1所示的多球面食用玫瑰花瓣离散元模型。导出后处理中的多球面群信息，共2 256个球面，并包含球面的X坐标、Y坐标、Z坐标以及接触半径。

图1 多球面构建的离散元花瓣模型Figure 1 Discrete element petal model based on multi sphere

1.2 构建柔性化的食用玫瑰花瓣模型

基于EDEM 2020版中的Bonding V2的元颗粒模型，构建柔性化的食用玫瑰花瓣离散元模型。元颗粒模型能够定义模型中的多球面之间的关系，创建用于工业、自然界中的柔性以及细长的材料，比如纤维、秸秆等。由于食用玫瑰花瓣的厚度较薄，厚度约为0.6～1.2 mm，为简化离散元建模难度，假设球面直径为1 mm。离散元多球面建模接触半径的设置用于检测颗粒是否发生黏结，当球面接触半径检测到接触后，生成黏结键，将两个球面黏结在一起。接触半径太小模型会发生碎裂，接触半径太大则会使模型之间相互黏结，为降低接触半径对仿真结果的影响，接触半径应比球面半径大20%～30%[8]。根据多球面的X、Y、Z位置信息，定义球面半径0.5 mm，接触半径0.6 mm，建立食用玫瑰花瓣离散元模型。根据表1与表2设置仿真时的材料物理参数与接触参数，根据表3设置食用玫瑰花瓣离散元仿真黏结参数。由于后续需要标定碰撞恢复系数和滚动摩擦系数，因此在建立离散元模型过程中，可以先假设碰撞恢复系数、滚动摩擦系数很小，通常设置为0.01。通过Bonding V2接触模型，构建的柔性食用玫瑰花瓣Bond模型见图2。

图2 食用玫瑰花瓣Bonding V2黏结模型Figure 2 Bonding V2 model of edible rose petals

表1 材料物理参数Table 1 Material physical parameters

表2 物料接触参数Table 2 Particle contact parameters

表3 食用玫瑰花瓣颗粒黏结参数Table 3 Bonding parameters of edible rose petal granules

2 食用玫瑰花瓣离散元参数标定

参数标定，通常也叫“参数匹配”，是通过物料特性试验与仿真相结合的一种确定物料仿真参数的常用方法，经过仿真环境下模拟出与真实试验相一致的虚拟试验，从而确定物料的离散元仿真参数[9]。离散元所需要的仿真参数，主要是物料的本征参数与接触参数，这些参数可通过相应的物料试验进行测量，对于难以通过试验测量的参数，需要基于虚拟堆积试验与物料堆积试验，进行仿真参数匹配。

2.1 虚拟堆积试验

食用玫瑰花瓣虚拟堆积试验以物理堆积试验数据为基础[10]，在EDEM 2020软件中，基于Bonding V2接触模型建立虚拟堆积试验仿真。添加空心圆筒，并在圆筒上方设置虚拟平面，作为颗粒工厂，静态生成200 g的食用玫瑰花瓣离散元模型。当生成的食用玫瑰花瓣离散元模型充满整个空心圆筒后，以2 m/s的速度提升空心圆筒，食用玫瑰花瓣虚拟堆积试验示意图见图3。

图3 食用玫瑰花瓣虚拟堆积试验示意图Figure 3 Virtual accumulation test of edible rose petals

食用玫瑰花瓣虚拟堆积试验，生成具有堆积中心的锥形体，与物理堆积试验相符合。使用软件内置量角测量工具，以虚拟堆积中心为测量原点，测量+X以及+Y两个方向上的堆积角[11]，结果取平均值。虚拟堆积试验堆积角测量示意图见图4。

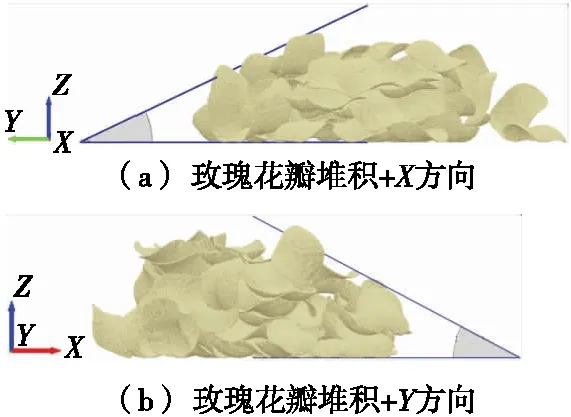
图4 虚拟堆积角测量示意图Figure 4 Schematic diagram of virtual stacking angle measurement

2.2 因子筛选试验

通过试验测量得到的离散元参数有食用玫瑰花瓣密度552.8 kg/m3、食用玫瑰花瓣—食用玫瑰花瓣静摩擦系数0.453、食用玫瑰花瓣—不锈钢静摩擦系数0.048 7。将标定参数进行Placket-Burman试验设计，如表4所示。6个需要标定的参数，最低需要完成12次试验，并增加一组中心点试验，总共13次虚拟堆积试验，将测量数据填入表5中。根据Minitab 19软件对试验结果进行方差分析[12]，得到表6所示Placket-Burman试验结果方差分析表。

表4 Placket-Burman试验参数表Table 4 Placket-Burman test parameters

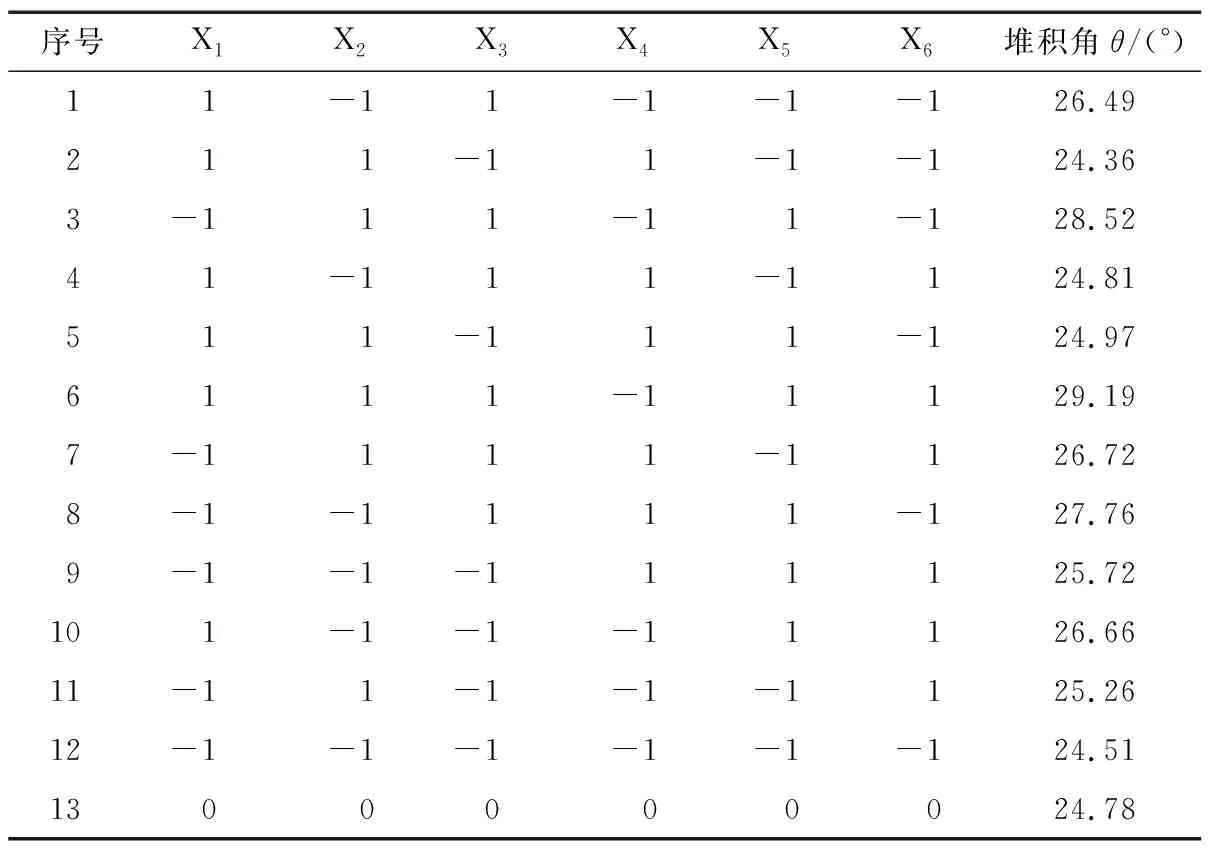
表5 Placket-Burman试验设计与结果Table 5 Placket-Burman test design and results

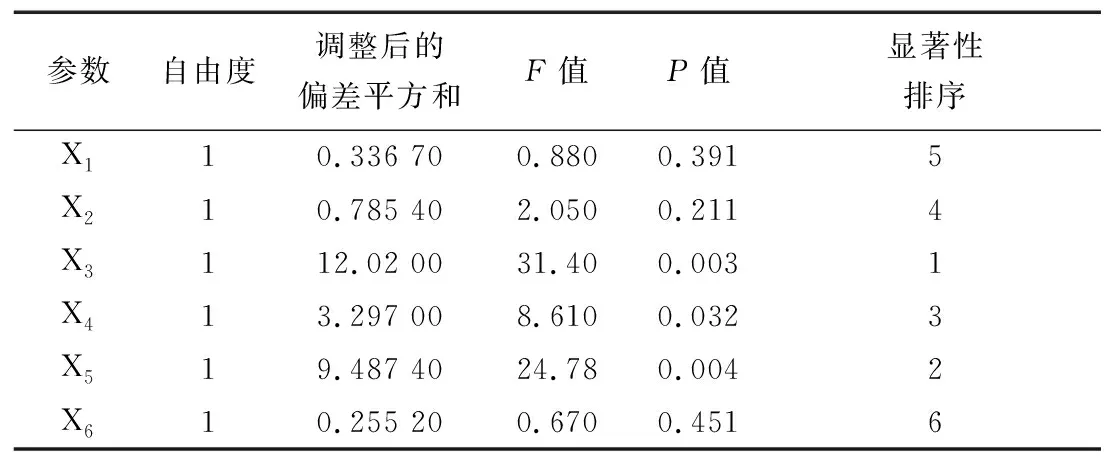
表6 Placket-Burman试验结果方差分析Table 6 Analysis of variance of Placket-Burman test results

2.3 最陡爬坡试验

根据筛选试验分析得到3个显著性参数，通过设定步长，在参数范围内逐渐增加，进行最陡爬坡试验。最陡爬坡试验设计与结果见表7。除3个显著性参数外，不显著参数设置：食用玫瑰花瓣泊松比取中心点，为0.3，食用玫瑰花瓣剪切模量只影响花瓣之间的碰撞受力，同时为了提高仿真运行效率，取4 MPa，花瓣—不锈钢滚动摩擦系数取中心点值，为0.03。随着3个显著性参数步长增加，物理堆积角与虚拟堆积角的相对误差呈先减小后增大的趋势，特别是在3号试验组，其误差最小。因此确定花瓣—花瓣碰撞恢复系数参数取值范围为0.03～0.07，花瓣—不锈钢碰撞恢复系数的显著性参数取值范围为0.03～0.07，花瓣—花瓣滚动摩擦系数显著性参数的取值范围为0.05～0.15。

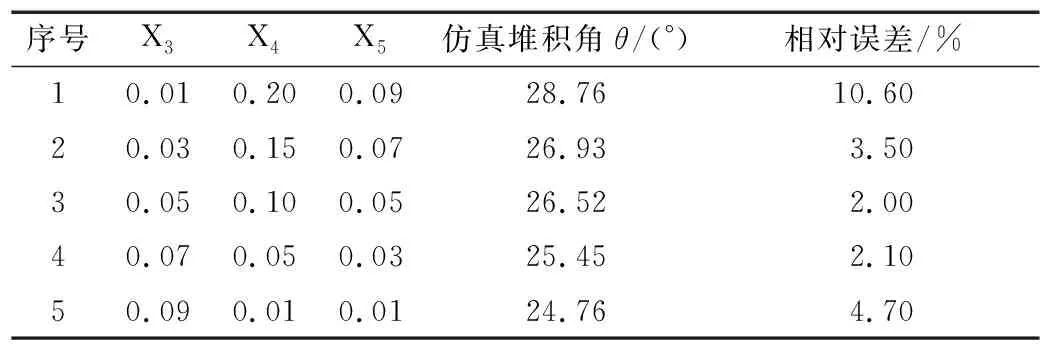
表7 最陡爬坡试验设计与结果Table 7 Design and results of steepest climbing test

2.4 Box-Behnken试验设计及结果分析

取3号试验结果作为中心水平，以2、4组试验参数作为水平，进行表8所示的显著接触参数水平编码。根据参数水平编码，设计虚拟堆积试验方案，将显著性参数的水平组合参数代入EDEM 2020软件中，进行虚拟堆积试验仿真，并测量堆积角，食用玫瑰花瓣虚拟堆积试验的Box-Behnken试验设计与结果见表9。

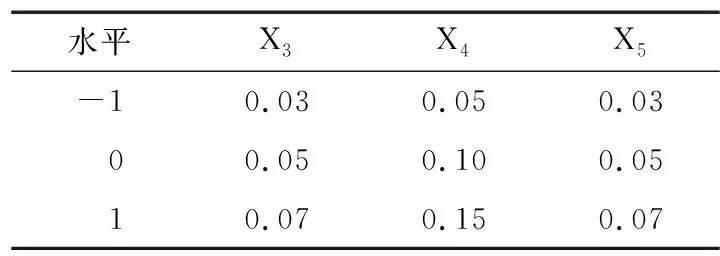
表8 显著性接触参数水平编码Table 8 Significant exposure parameter level coding

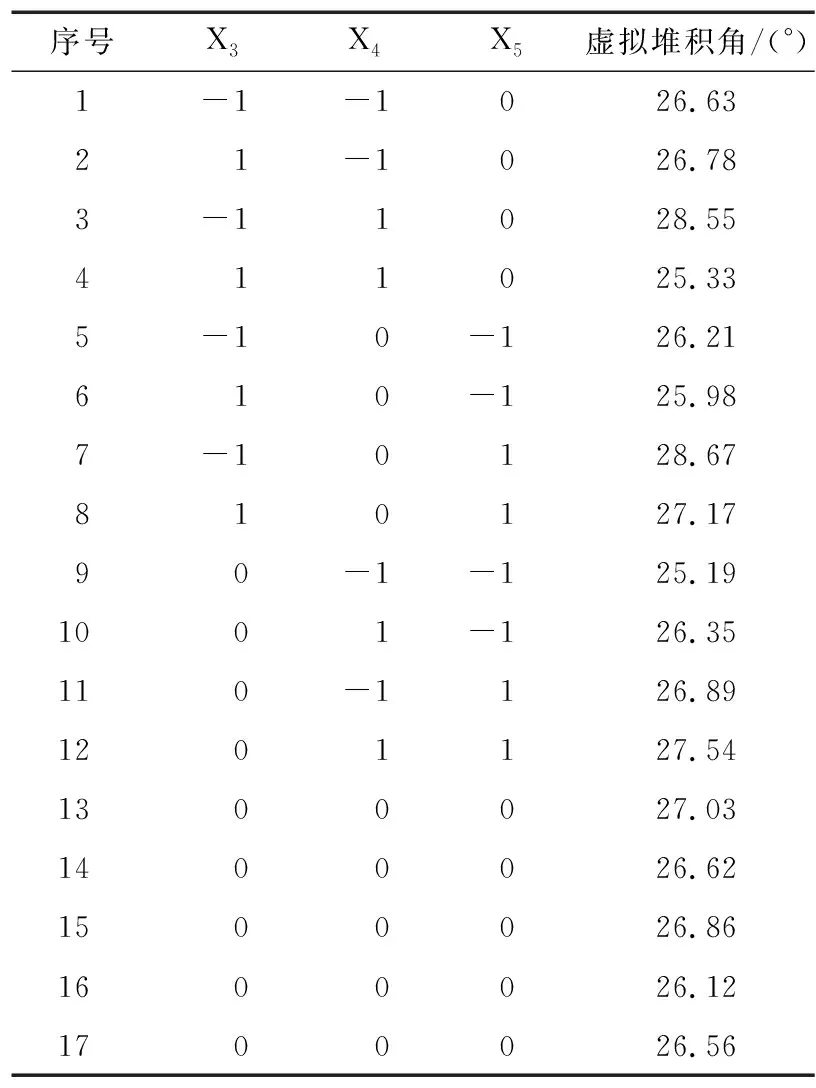
表9 Box-Behnken试验设计与结果Table 9 Box-Behnken design and results

对试验结果进行多元回归分析，得到3个显著性参数与堆积角(θ)的二次多项式方程为：

(1)

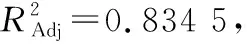
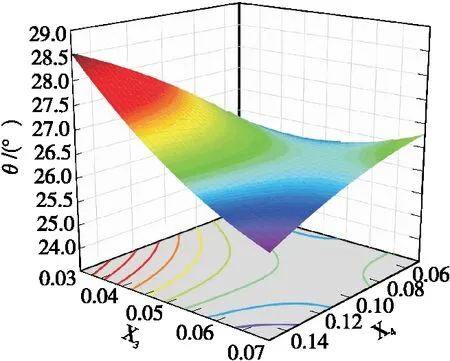
图5 交互因素对堆积角的影响Figure 5 Influence of interaction factors on stacking angle

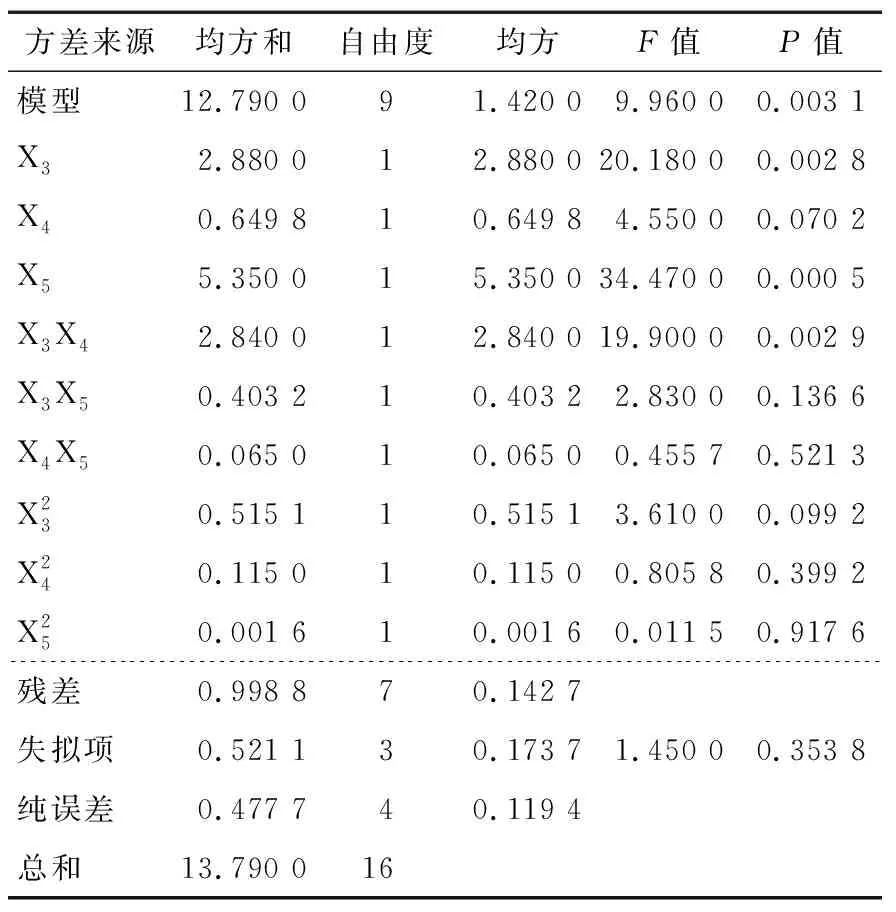
表10 Box-Behnken试验回归模型方差分析Table 10 Analysis of variance of Box-Behnken test regression model

2.5 参数优化及试验验证

以物理堆积角26°为响应目标值，优化参数范围为25.5°～26.5°，利用Design-Expert 12软件对显著性参数与堆积角的二次多项式进行寻优求解[13]，选择与物理堆积角相对误差最小的一组组合为最优取值，即花瓣—花瓣碰撞恢复系数为0.05，花瓣—花瓣滚动摩擦系数为0.051，花瓣—不锈钢碰撞恢复系数为0.046。其余非显著性参数的取值为泊松比0.3，剪切模量4 MPa，花瓣—花瓣静摩擦系数0.453，花瓣—不锈钢静摩擦系数0.487，花瓣—不锈钢滚动模型系数0.03。为验证优化的参数准确性，对优化后的参数进行5次虚拟堆积试验，虚拟堆积试验与物理堆积试验对比见图6。测量虚拟堆积角分别为26.13°，26.46°，26.71°，25.98°，26.61°，平均值为26.378，与物理堆积角的相对误差为1.45%，应用T检验对虚拟堆积角与物理堆积角进行分析，得到P=0.054>0.05，表明虚拟堆积角与物理堆积角无显著性差异。

图6 虚拟堆积试验与物理堆积试验对比Figure 6 Comparison between virtual stacking test and physical stacking test

3 结论

研究结果表明，采用离散元方法建立柔性食用玫瑰花瓣离散元模型，通过物理堆积试验与虚拟堆积试验相结合，依次进行Placket-Burman试验、最陡爬坡试验和Box-Behnken试验对堆积角影响显著的因素进行寻优求解，能够对食用玫瑰花瓣离散元仿真参数进行标定。但该研究仅建立了尺寸单一的食用玫瑰花瓣离散元模型，且构成模型的球形颗粒数量较多，在一定程度上影响了参数标定的速度与效率，后续可以建立不同尺寸的食用玫瑰花瓣离散元模型，进一步提高食用玫瑰花瓣参数标定的准确性。