神奇的“惯性力”

吴 滨 詹 凯

(1.北京市101中学 2.首都师范大学附属中学)

在普通高中物理教学与学习中,很少涉及惯性力这个概念,因为高中课程标准中不涉及不同参考系中相对运动的定量计算,更不会探讨两个做相对加速运动的参考系中物体的运动关联或动力学的相关问题.然而这部分内容在强基考试、物理竞赛中却是运动学、动力学问题的重点和核心内容.如果一个学生想系统学习强基知识或者物理竞赛内容,那惯性力常常是他们遇到的第一个难点.

在实际教学中,我们曾经尝试让学生自学惯性力的内容,然后提出一个问题:“能讲讲科里奥利力是怎么回事吗?”学生答曰:“哦,就是微分微出来的一个力!”笔者只能报以一笑.诚然,惯性力确实有其抽象的一面,与中学课内所学过的力不同,惯性力似乎找不到其“施力者”,这就让初学者丈二和尚摸不着头脑.然而地球在绕太阳公转,自己也在自转,所以地球就是一个天然的转动参考系.想要搞清楚地球上发生的一些神奇现象,惯性力又是绕不开的概念.

本文不打算从烦琐的数学角度出发,严格推导出惯性力,这样过于抽象.我们将分别从平动加速的车中小球的运动和转动的圆盘上小球的运动两个简单实例出发,让读者真正“看到”惯性力的存在,再去探讨汽车加速前进、落体偏东、傅科摆、潮汐的形成等一些实际问题.

1 什么“力”让车中的小球动起来?

如图1所示,在小车上放置一光滑的水平桌面,再将质量为m的小球放在水平桌面上,桌面上除小球(小球的线度远远小于小车的横向线度)之外别无他物,即小球水平方向合力为零.然后突然使小车向右对地做加速运动,小球如何运动呢?

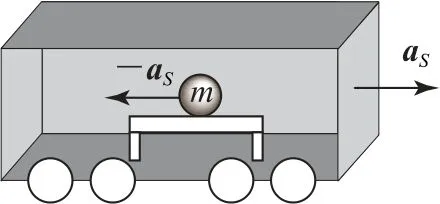
图1

地面上的观察者认为:小球将静止在原地,符合牛顿第一定律;车上的观察者觉得:小球以－aS的加速度相对于小车做加速运动.

我们假设车上的人熟知牛顿运动定律,尤其对“加速度是由力引起的”印象至深,以致在任何场合下,他都强烈地要求保留这一认知,于是车上的人说:小球之所以相对小车有－aS的加速度,是因为受到了一个指向左方的作用力,且力的大小为maS,物理上把这个力命名为惯性力.

以下推导引入惯性力后,就可以使非惯性系中的观察者仍可以用牛顿运动定律的语言和公式来解释小球的运动,因而具有“实用性”的意义.惯性力使非惯性系中牛顿运动定律方程的形式,与以地面为参考系的牛顿运动定律在数学上完全等效.

设a为质量为m的一质点对地的加速度,aS为某参考系S′对地的加速度,F为该质点所受合力.

由牛顿第二定律得F＝ma,质点m相对参考系S′的加速度a′＝a－aS,两式联立得F＝ma′＋maS,移项得F－maS＝ma′,其中“－maS”可以看成一个力,叫作平移惯性力,它与真实力的合成使质点产生相对新参考系的加速度a′.

要正确理解“惯性力”需要把握以下要点:1)惯性力不是物体间的相互作用.因此,没有反作用力,实质上,从惯性系来看,它只不过是物体惯性的表现.2)惯性力的大小等于研究对象的质量m与非惯性系的加速度aS的乘积,而方向与aS相反,即f*＝－maS.3)我们把牛顿运动定律成立的参考系叫惯性系,不成立的参考系叫非惯性系.设一个参考系相对绝对空间加速度为aS,物体相对此参考系的加速度为a′,牛顿运动定律可以写成F＋f*＝ma′,其中F为物体受到的“真实的力”,f*为惯性力,是个“假力”.4)如果研究对象是刚体,则惯性力等效作用点在质心处.

总之,在非惯性系中,牛顿运动定律不再成立.为了形式上仍能利用牛顿运动定律,在相对惯性系做匀加速直线运动的非惯性系中分析物体受力时,除了各种原惯性系受到的力外,认为任何物体都还受到一个惯性力－maS.这样牛顿运动定律仍可使用,aS为此非惯性系相对惯性系的加速度.

2 加速前进的车能不能“飞起来”?

例1(2019年清华领军)轿车通常有前轮驱动和后轮驱动两种,当轿车启动时,下列说法正确的是( ).

图2

A.前轮驱动时,轿车前轮部分微微下沉

B.前轮驱动时,轿车后轮部分微微下沉

C.后轮驱动时,轿车前轮部分微微下沉

D.后轮驱动时,轿车后轮部分微微下沉

E.无论是前轮驱动还是后轮驱动,轿车整体都会微微下沉

解析此题我们可以在汽车参考系中分析.汽车参考系是非惯性系,需要引入惯性力f*＝－ma,则汽车在此参考系静止.如图3 所示,若轿车为后轮驱动,启动时,后轮受到的摩擦力Ff1向前,前轮受到的摩擦力Ff2向后,假设轿车的重心位于两轮间的O点.设前后轮间距为L,O点距地面高度为h.由受力平衡得f*＋Ff2＝Ff1,选前轮与地面的接触点为支点,由力矩平衡得f*·h＝FN2·L,a越大,惯性力f*越大,FN2越大,所以轿车后轮部分微微下沉.同理,若轿车为前轮驱动时,轿车也是后轮部分微微下沉.选项B、D 正确.

图3

点评在进行质点的力与运动的分析时,需考虑惯性力;在分析刚体的转动问题,考虑力矩时也需要加上惯性力的力矩.同学们也可以自行思考,当轿车启动加速度多大时,前轮会离开地面?

3 转动的小球受到哪些力?

例2图4所在平面为某惯性系S的一个平面,S′系绕着过O′点垂直于图平面的固定轴相对于S系匀速旋转,角速度为ω,图中圆象征S′系中垂直于转轴的一个平面.

图4

(1)若质点随S′一起旋转,在S′系中,需要引入怎样的惯性力才能让质点在该系中静止?

(2)若质点在S系中静止,此时质点相对于S′系做匀速圆周运动.还需要引入怎样的惯性力,才能让质点在S′系中转动?

解析(1)设质点m静止在此平面上,相对于圆心的径矢为r′.质点在S系中做匀速圆周运动,加速度a和真实力分别为a＝－ω2r′,F＝ma＝－mω2r′,相对于S′系有a′＝0,F′＝ma′＝0.

S′系必须认可真实力F的存在,于是需要引入FC＝mω2r′,使得F′＝F＋FC＝0,FC方向与r方向相同,背离旋转中心,称为惯性离心力,简称离心力.

(2)设质点m相对S系静止,测得质点所受真实力F＝0.在S′系中,质点在如图5中所示的虚线中做圆周运动,向心加速度为a′＝－ω2r′,合力F′需等于圆周运动向心力F′心,即有F′＝F′心＝ma′＝－mω2r′,质点所在位置r′对应的离心力为FC＝mω2r′.于是如图5所示,在S′系中为质点引入虚拟力FCor＝－2mω2r′,才可使得F′＝F＋FC＋FCor＝ma′成立.

图5

FCor由法国学者科里奥利(G.Coriolis)于1835年首先提出,故命名为科里奥利力.科里奥利力因质点相对于S′系运动而引入,上面的表达式却未能表现质点运动因素,所以要试着将其改造.按通常习惯,在右手系中将角速度ω矢量化为ω,方向垂直于图平面向上,质点相对于S′系的速度v′方向也已在图中示出,大小为ωr′,可得v′×ω＝－ω2r′,科里奥利力便可改述成FCor＝2mv′×ω.

点评惯性离心力是匀速旋转非惯性系S′需引入的第一类虚拟力,这种力仅由S′系中质点所在位置r′确定.为易于阐述,特取质点相对S′系处于静止的特殊状态引入惯性离心力,结果则适用于质点在S′系中可取的任何运动状态.科里奥利力与惯性离心力不同,一方面,这两个惯性力是两种不同的惯性力,另一方面科里奥利力中出现的速度v′,指的是物体相对于转动参考系运动时的相对速度.另外还需注意科里奥利力的方向的判断需要用到矢量叉乘的规律.利用科里奥利力和惯性离心力,可以解释很多在地球上发生的“神奇”现象.

不仅如此，云南的山珍野生菌，已经随着“山大王”品牌走向了国际市场，产品销往日本、东南亚国家，以及意大利、法国等，在欧美市场也占有一席之地。

4 自由下落的物体为什么“打偏了”?

例3(2018年北京卷)根据高中所学知识可知,做自由落体运动的小球,将落在正下方位置.但实际上,赤道上方200m 处无初速度下落的小球将落在正下方位置偏东约6cm 处,这一现象可解释为,除重力外,由于地球自转,下落过程小球还受到一个水平向东的“力”,该“力”与竖直方向的速度大小成正比,现将小球从赤道地面竖直上抛,考虑对称性,上升过程该“力”水平向西,则小球( ).

A.到最高点时,水平方向加速度和速度均为零

B.到最高点时,水平方向加速度和速度均不为零

C.落地点在抛出点东侧

D.落地点在抛出点西侧

解析由于该“力”与竖直方向的速度大小成正比,所以从小球抛出至运动到最高点的过程中,该“力”逐渐减小到零,将小球的上抛运动沿水平方向和竖直方向分解,由于上升阶段,水平分运动是向西的变加速运动(水平方向加速度大小逐渐减小),故小球到最高点时速度不为零,水平向西的速度达到最大值,故选项A 错误;小球到最高点时竖直方向的分速度为零,由题意可知小球这时不受水平方向的力,故小球到最高点时水平方向加速度为零,选项B 错误;下降阶段,由于受水平向东的力,小球的水平分运动是向西的变减速运动(水平方向加速度大小逐渐变大),故小球的落地点在抛出点西侧,选项C 错误,选项D 正确.

一般情况下,在地球参考系中,惯性离心力和科里奥利力并不大,虽然引起的相对误差较小,但还是能在一些现象中体现出来.我们可以用科里奥利力解释“北半球的河流对右岸冲刷得较厉害,而南半球的河流则对左岸冲刷较厉害”这一现象.地球自西向东转,其角速度矢量ω由南指向北,在北半球垂直地面的分量向上,从而v×ω总指向运动方向v的右边.在南半球ω垂直地面的分量向下,从而v×ω总指向运动方向v的左边,故北半球的河流冲刷右岸,南半球的河流冲刷左岸.

例4(2020年北大强基)单摆在摆动过程中,其摆动平面会逐渐发生转动(进动),这是因为( ).

A.地心引力不均匀

B.月球对地球的潮汐力

C.地球在自转,造成地转偏向力

D.以上都不对

解析单摆振动时,振动面依理应保持不变,但因地球在自转,在地面上的观察者,不能发觉地球在转,但在相当长的时期内,却发现摆的振动面不断偏转.从力学的观点来看,这也是由于受到了科里奥利力影响的缘故.上述能显示地球自转的装置,是1851年傅科在巴黎首先制成的,在傅科摆实验中,人们看到,摆动过程中摆动平面沿顺时针方向缓缓转动,摆动方向不断变化.摆在摆动平面方向上并没有受到外力作用,摆动的空间方向不会改变,因而可知,这种摆动方向的变化是观察者所在的地球转动的结果.观察者看到的是相对转动参考系运动的现象,从而有力地证明了地球是在自转.选项C正确.

点评傅科摆放置的位置不同,摆动情况也不同.在北半球时,摆动平面顺时针转动;在南半球时,摆动平面逆时针转动.而且纬度越高,转动速度越快,在赤道上的摆几乎不转动.

5 到底什么是“引潮力”?

地球上海水的周期性涨落称为潮汐.月球和太阳都对地球上的海水有引力作用,潮汐主要是月球对海水的引力造成的.潮汐现象的特点是每昼夜有两次涨落潮,即在地表离月球最近和最远的地方形成涨潮,而在地月连线两侧处于落潮.如果说潮汐是万有引力引起的,那么太阳对海水的引力比月球对海水的引力大180倍,为什么是月球对潮汐起主要作用呢? 地—月系统在引力的相互作用下围绕着共同的质点O旋转.在地心参考系这个非惯性系中,各地海水所受相对地心这个非惯性系的有效作用力,即引潮力,相当于“真实的月球引力”和“惯性离心力”的合成,其中惯性离心力等于物体质量和月球对地球引力在地球球心处所产生的加速度的乘积,方向沿月地的连线向外.

如果研究各处的有效作用力,计算较为复杂,不妨先考虑离月球最远和最近的两处,如图6所示,研究地球上A、B两地质量为Δm的海水,设地球半径为R地,地心与月心的距离为r地月,月球质量为M月,则海水所受惯性力F惯＝Δma,因为月球对地球引力所产生的加速度,所以

图6

A处引潮力

其他地方的引潮力由于引力和惯性离心力不在同一直线上,要运用平行四边形定则分析.各处的引潮力在地表分布如图7所示,它把地球表面的海水沿地月连线方向拉长成为一个椭球,离月球最近和最远处形成海水的高峰,地月连线两侧形成海水的低谷.各处引潮力的大小均与地月间的距离三次方成反比.随着地球的自转,一昼夜之间有两个高峰和两个低谷扫过每个地方,形成两次高潮和两次低潮.

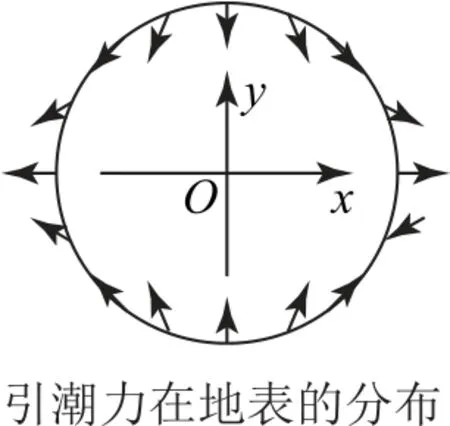
图7

同理可以分析计算太阳的引潮力,经计算可知,太阳引潮力与日地间距离的三次方成反比.代入相关数据可知,太阳引潮力大小约为月球引潮力的一半.当太阳的引潮力和月球的引潮力同向叠加时,则为大潮;当太阳的引潮力与月球引潮力反向叠加时,则为小潮.由此可见,引潮力不能仅仅归结为月球的作用,否则无法解释大潮、小潮现象.

牛顿发现引力规律距今仅有300多年,但我国古代的劳动人民发现潮汐的规律已经有上千年的历史了.先人这样的细心观察与总结,激励着我们热爱科学、崇尚科学.

(完)