对挂钩模型的深度思考

2022-09-14杨天才

高中数理化 2022年16期

王银杨天才

(1.安徽省寿县一中 2.重庆市大学城第一中学校)

为了形象、简捷地处理物理问题,人们经常把复杂的实际情况转化成一定的容易接受的简单的物理情境,从而形成一定的经验性的规律,即建立物理模型.高考试题体现了考试作为教育的重要手段和必要环节,对中学教学有一定的导向作用.本文以2017年高考天津卷第8题为切入口,归纳总结挂钩模型的特点,并通过对同类模型的进阶拓展,深度解析其物理本质,提升学生的物理学科核心素养.

2 思维链条

2.1 模型呈现

例1(2017年天津卷)如图1所示,轻质不可伸长的晾衣绳两端分别固定在竖直杆M、N上的a、b两点,悬挂衣服的衣架钩是光滑的,挂于绳上处于静止状态.如果只人为改变一个条件,当衣架静止时,下列说法正确的是( ).

图1

A.绳的右端上移到b′,绳子拉力不变

B.将杆N向右移一些,绳子拉力变大

C.绳的两端高度差越小,绳子拉力越小

D.若换挂质量更大的衣服,则衣服架悬挂点右移

解析对衣架钩受力分析如图2所示,设绳与水平方向的夹角为θ,由平衡条件知2FTsinθ＝mg,则.设绳子总长为L,衣架两侧绳长为L1、L2,两杆间距离为d,根据几何关系有L1cosθ＋L2cosθ＝d,得cosθ＝.绳的右端上移到b′,L、d、衣服及挂钩的重力mg都不变,则绳子张力FT也不变,选项A 正确;杆N向右移动一些,d变大,FT变大,选项B正确;绳的两端高度差无论如何变化,不影响d和L,所以FT不变,选项C 错误;衣服质量增加,绳子上的拉力增加,由于θ不变,则衣服悬挂点不变(不会右移),选项D 错误.

图2

通过对例题的分析,总结出光滑挂钩模型的特点:1)成立的条件:不计一切摩擦且系统处于平衡状态;2)由,两绳与水平方向的夹角(相同)仅与两杆间距、绳总长有关,与悬挂物重力、绳中张力、悬挂点(确定)位置无关;3)由知,绳中张力大小处处相等且仅与悬挂物重力、两杆间距、绳总长有关,与绳子左右结点的高度差无关,当绳两端点水平距离增加(或减小)时,由于绳长不变,故绳与竖直方向的夹角增大(或减小);4)悬挂点的位置仅与两杆间距、绳总长、绳端固定点有关,与悬挂物重力、绳中张力无关;5)光滑挂钩其作用相当于轻动滑轮,还可等效为光滑钉子、轻圆柱体等.

2.2 模型应用

根据挂钩模型的特点,可以设置与模型相关的比较大小、临界条件、动态变化等基本问题.

例2如图3所示,一光滑轻绳左端固定在竖直杆顶端,其右端系于一光滑圆环上,圆环套在光滑的矩形支架ABCD上.现将一物体用轻质光滑挂钩悬挂于轻绳之上,若使光滑圆环沿着ABCD方向在支架上缓慢地顺时针移动,圆环在A、B、C、D四点时,绳上的张力分别为Fa、Fb、Fc、Fd,则( ).

图3

A.Fa＜FbB.Fb＞Fc

C.Fc＞FdD.Fd＞Fa

解析根据前文结论,圆环沿AB方向和CD方向移动时,张力均不变,即Fa＝Fb,Fc＝Fd,选项A、C错误;沿BC方向移动时,作用点间距增大,张力增大,即Fb＜Fc,Fd＞Fa,选项D 正确.

点评本题与模型结论十分吻合,解决此类问题时,首先要通过受力分析,掌握其受力特点,建立正确的物理模型,再根据相关结论求解.

例3如图4所示,将一根轻而柔软的细绳一端拴在天花板上的A点,另一端拴在墙壁的B点,A和B到O点的距离相等,绳的长度是OA的两倍,在一质量可忽略的动滑轮K的下方悬挂一质量为m的重物,摩擦力可忽略.现将动滑轮、重物一起挂到细绳上,在达到新的平衡时,绳中拉力为多大?B点沿墙壁向O点缓慢移动过程中,绳中拉力最小值为多大?

图4

解析由前文结论知.如果此时将B点沿墙壁向O点缓慢移动,F不变,拉力最小值为

点评本题要求定量计算绳中张力的大小和张力的极值,是模型的具体应用.

例4如图5所示,以水平直杆AB的中点O为转轴,一轻绳跨过轻质滑轮,两端分别固定在A、B两点,滑轮通过另一根轻绳连接一重物,不计滑轮与轻绳之间的摩擦.现让直杆AB绕O逆时针缓慢转过角度θ(θ＜90°),轻绳的张力( ).

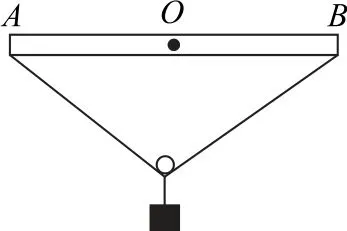
图5

A.逐渐减小 B.逐渐增大

C.先增大后减小 D.先减小后增大

解析直杆AB绕O逆时针缓慢转过角θ(θ＜90°)的过程中可认为重物处于平衡状态,因间距减小,轻绳的张力逐渐减小,选项A 正确.

点评本题在原有模型基础上,增加了静力学的动态平衡背景,因两个分力的大小和方向都在改变,这里不能用求解动态平衡问题的矢量三角形法和相似三角形法判断,要求学生在解题时整合必备知识,以此提升关键能力.

2.3 模型拓展

挂钩模型的成立条件是不计一切摩擦且系统处于平衡状态,如果晾衣绳粗糙、“活结”变“死结”、有外力作用、系统处于加速状态等,其结论有何不同呢?

例5如图6所示,轻质不可伸长的晾衣绳两端分别固定在竖直杆M、N上的a、b两点,a点比b点低,晾衣绳粗糙,悬挂衣服的衣架钩在晾衣绳中点和在杆M、N中间位置时都不滑动.衣架静止,下列说法正确的是( ).

图6

A.衣架钩在晾衣绳中点时,左右两边绳子拉力大小相等

B.衣架钩在晾衣绳中点时,右边绳子拉力小于左边绳子拉力

C.衣架钩在杆M、N中间位置时,左右两边绳子拉力大小相等

D.衣架钩在杆M、N中间位置时,右边绳子拉力大于左边绳子拉力

解析设a到节点的高度为h1,b到节点的高度为h2,节点到M的水平距离为x1,节点到N的水平距离为x2,a端绳子和水平方向的夹角为α,b端绳子和水平方向的夹角为θ,对绳子节点进行受力分析,如图7所示.当衣架钩在晾衣绳中点时,设a、b到节点绳子长度为L,根据几何关系有

图7

因为h1＜h2,可得α＜θ,根据平衡条件有Facosα＝Fbcosθ,可得,选项A、B错误;衣架钩在杆M、N中间位置时,根据几何关系有

因为h1＜h2,可得α＜θ,根据平衡条件有Facosα＝Fbcosθ,可得,Fa＜Fb,选项C错误,选项D 正确.

点评本题涉及绳受摩擦力问题,是模型的进阶拓展.原有模型(“活结”)的结论要重新进行修正(“死结”),不能直接套用结论.对悬挂物进行正确的受力分析、正交分解,最后利用力的平衡条件列方程求解是关键.如果把重物(衣服)换成其他质点(如杂技演员),只要是在摩擦力作用下系统处于静止状态,新结论依然成立.

例6如图8 所示,轻质不可伸长的晾衣绳两端分别固定在两根竖直杆上,A端高于B端,绳上挂有一件衣服,为防止滑动,将悬挂衣服的衣架钩固定在绳上,当固定在适当位置O处时,绳子两端对两杆的拉力大小相等.则( ).

图8

A.绳子OA段与竖直杆夹角比OB段与竖直杆夹角大

B.O点位置与衣服重力有关,衣服重力越大,O点离B端越近

C.若衣架钩固定在绳子上中点处,则绳子两端对杆的拉力大小仍然相等

D.若衣架钩固定在绳子上中点处,则绳子A端对杆的拉力大于B端对杆的拉力

解析设左、右两段绳的拉力大小分别为F1、F2,左、右两段绳与竖直方向的夹角分别为α、β,根据水平方向受力平衡可得F1sinα＝F2sinβ,由于F1＝F2,故α＝β,选项A 错误;根据上面的方程可知,O点的位置取决于绳长和两杆间的距离,与衣服重力无关,选项B错误;若衣架钩固定在绳子的中点处,由于杆A高于杆B,即α＞β,结合F1cosα＝F2cosβ,可得F1＞F2,选项C错误,选项D 正确.

点评本题因悬挂点固定,相当于“死结”模型,结论与例5相似,例5和例6学生易与不打结的绳混淆而认为绳上的拉力始终相等,要求学生对具体问题要具体分析.

例7如图9 所示,一根不可伸长的长为L的轻绳两端分别固定在间距为d的两竖直杆的P点和Q点上,晾衣架上挂着湿衣服,衣架上的钩挂在轻绳上可来回自由滑动.若忽略衣架挂钩与轻绳间的摩擦,则下列说法正确的是( ).

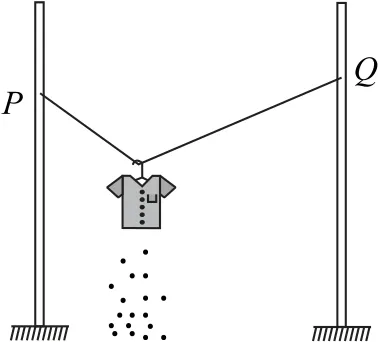
图9

A.在湿衣服上的水滴下落过程中,轻绳中的张力不断减小

B.衣服不滴水时,将P点稍向上移动,则轻绳中的张力增大

C.衣服不滴水时,将左侧竖直杆稍向左移动,则轻绳中的张力减小

D.衣服不滴水时,刮起了向左的风,若风力大小恒定,再将P点稍向上移动,轻绳中的张力将增大

解析由前文结论,湿衣服上的水滴下落过程中,衣服重力mg减小,则轻绳中的张力不断减小,选项A 正确;衣服不滴水时,将P点稍向上移动,轻绳中的张力不变,选项B错误;衣服不滴水时,将左侧竖直杆稍向左移动,轻绳中的张力增大,选项C 错误;衣服不滴水时,刮起了向左的风,若风力大小恒定,此时两段轻绳的拉力的合力方向偏向右上方,如图10所示,由于重力和向左的风力的合力大于衣服的重力,所以此时细绳拉力增大;再将P点稍向上移动,相当于增大了两根杆之间的距离,即距离由d′变为d″,则轻绳中的张力增大,选项D 正确.

图10

点评本题在原模型基础上,继续改变条件创设新情境,使悬挂物受到水平恒力(外力)的作用,需要学生根据原有相关的解题方法来解决新问题.

2.4 模型升华

物理问题源自“原汁原味”的自然现象和实际生活,前面的例题都是原模型及其拓展的理论推导.那这一模型可以用实验检验吗?

例8为了研究人们用绳索跨越山谷过程中绳索拉力的变化规律,同学们设计了如图11所示的实验装置.他们将不可伸长轻绳的两端通过测力计(不计质量及长度)固定在相距为D的两立柱上,固定点分别为P和Q,P低于Q,绳长为L(L＞PQ).他们首先在绳上距离P点10cm处(标记为C)系上质量为m的重物(不滑动),由测力计读出PC、QC的拉力大小FTP、FTQ.随后,改变重物悬挂点C的位置,每次将P到C的距离增加10cm,并读出测力计的示数,最后得到FTP、FTQ与绳长PC的关系曲线,如图12所示.由实验可知,曲线Ⅰ、Ⅱ相交处,可读出绳的拉力为FT0＝________N,它与L、D、m和重力加速度g的关系为FT0＝________.