2022年高考湖北卷物理压轴题探析和拓展研究

2022-09-14黄尚鹏

高中数理化 2022年16期

黄尚鹏

(湖北省监利市实验高级中学)

1 对原题的分析与解答

例(2022年高考湖北卷第16题)打桩机是基建常用工具.某种简易打桩机模型如图1 所示,重物A、B和C通过不可伸长的轻质长绳跨过两个光滑的等高小定滑轮连接,C与滑轮等高(图中实线位置)时,C到两定滑轮的距离均为L.重物A和B的质量均为m,系统可以在如图1 虚线位置保持静止,此时连接C的绳与水平方向的夹角为60°.某次打桩时,用外力将C拉到图中实线位置,然后由静止释放.设C的下落速度为时,与正下方质量为2m的静止桩D正碰,碰撞时间极短,碰撞后C的速度为零,D竖直向下运动距离后静止(不考虑C、D再次相碰).A、B、C、D均可视为质点.

图1

(1)求C的质量;

(2)若D在运动过程中受到的阻力F可视为恒力,求F的大小;

(3)撤掉桩D,将C再次拉到图中实线位置,然后由静止释放,求A、B、C的总动能最大时C的动能.

解析(1)设C的质量为M,系统在如图1 虚线位置保持静止时,对C物体受力分析如图2所示,由平行四边形定则和平衡条件得Mg＝2mgsin60°,解得

图2

(2)设C的下落速度为v0＝时,与正下方质量为2m的静止桩D正碰后,桩D获得的速度为v,选向下为正方向,由动量守恒定律得Mv0＝2mv,解得v＝

(3)如图3所示,将C由静止释放后,设连接C的绳与水平方向的夹角为θ时,下落的高度为h,由机械能守恒定律可知,当系统的总动能最大时,系统的总势能最小,系统势能减少最多,下面我们用三种方法寻找系统总动能最大时的位置.

图3

方法1选θ为自变量,系统的总动能

方法2选h为自变量,系统的总动能

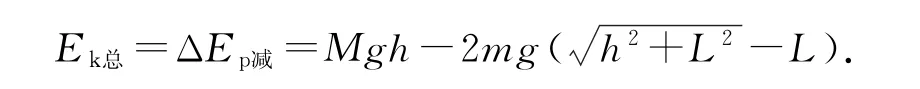
要使系统的总动能最大,对Ek总求导,并令导数为零,得

方法3根据重力做功与重力势能变化的关系WG＝－ΔEp可知,当系统的重力做正功时,系统的重力势能减少,当系统的重力做负功时,系统的重力势能增加,故当系统的重力总功率为零时,系统势能取极值,或者对系统应用动能定理,当系统的合外力做功最多时,系统的总动能增加最多,故当系统的重力总功率为零时,系统的总动能最大,设此时A物体的速度为vA,C物体的速度为vC,则2mgvA＝MgvC,即

如图4所示,根据绳连接体关联速度的特征可知,A、C两物体在沿绳方向的分速度相等,即

图4

由式①②同样得到θ＝60°,说明系统在静止时的平衡位置总动能最大.

当θ＝60°时,由方法1可知

小结1)本题以打桩机为情境,通过绳连接体模型,综合考查动量守恒定律、机械能守恒定律和动能定理等主干知识,是一道典型的考查动量与能量的综合题.本题第(1)问考查三力平衡模型,第(2)问借助碰撞模型考查动量守恒定律,借助木桩的减速运动过程考查动能定理的应用(当然也可运用运动学公式和牛顿第二定律联立求解),这两问都很基础,不偏不怪.第(3)问难度较大,第一步需要寻找系统总动能最大时的位置,常规思路是根据机械能守恒定律得出系统总动能的表达式,然后利用数学工具求极值,考查利用数学知识解决物理问题的能力.方法1和方法2都利用了导数工具,根据一阶导数为零求出极值出现的位置.方法1选θ为自变量,根据三角函数的导数公式求解;方法2选h为自变量,根据复合函数的导数公式求解;方法3是纯物理解法,根据“系统的重力总功率为零时系统的总动能最大”这一条件巧解,属于特殊快捷解法,要求考生具备敏锐的洞察力,一般考生难以想到.第(3)问第二步要求学生利用绳连接体关联速度知识求解,即根据“两物体在沿绳方向的分速度相等”这一特征求解.由于左右两边都有绳拉着C物体,学生容易错误地认为A、B两物体速度矢量合成即为C物体的速度,这就要求教师在平时的教学中讲清楚绳连接体关联速度分解的原理,否则学生容易死记结论并且想当然地犯下错误.

2)在第(3)问第一步中,我们已经得出系统在静止时的平衡位置总动能最大,这是一种巧合还是必然呢? 其实理论力学中根据分析力学原理可得出这样一个基本结论——保守力学体系在系统的平衡位置势能取极值.本题就是根据这一结论改编而成的,即系统在静止时的平衡位置势能最小,总动能最大,这是一种必然的结果.为进一步理解这一思想,我们再看一个典型例子.如图5 所示,一半径为R的光滑大圆环固定在水平面上,其最高点为A,另一质量为m的中心有孔的光滑小球套在大圆环上.一原长为l0(l0＜2R)、劲度系数为k的轻质弹簧一端固定于A点,另一端系在小球上.求小球静止时,弹簧与竖直方向的夹角θ.

图5

我们知道如果一个力所做的功与具体路径无关,这种力叫作保守力.在保守力场中,保守力所做的功等于势能的减少.保守力学体系处于平衡状态时势能取极值,根据系统势函数一阶导数为零,可得出系统在保守力以及约束力等作用下的平衡位置,因此此平衡问题也可用能量的观点求解.如图6所示,选最高点A所在的水平面为重力势能参考面,则系统的势函数

图6

以θ为自变量,对势函数求一阶导数,并令导数为零,寻找平衡位置,即＝4mgRsinθcosθ－2kR(2Rcosθ－l0)sinθ＝0,解得

为验证上述解法是否正确,不用能量的观点求解本题.如图7所示,对小球受力分析,由三力平衡和几何关系得

图7

2 对原题的拓展研究

拓展1求C物体由静止释放后能够下落的最大高度.

拓展2求C物体由静止释放后能够获得的最大速度.

【分析与解答】这种情况学生容易错误地认为在系统静止时的平衡位置,即θ＝60°时,C物体速度最大.产生这种错误认识的根本原因是学生认为当C物体的加速度为零时,C物体速度最大,此时A物体的加速度也为零,A物体也达到最大速度,即认为在运动过程中两物体的加速度同时为零,两物体同时达到最大速度,这是一种非常典型的错误认识.其实根据关联速度方程vA＝vCsinθ可知,当C物体速度最大时,C物体的加速度为零,可认为在此时刻附近的微小时间间隔内,C物体匀速运动,但随着θ的增大,sinθ增大,A物体会继续加速,即物体A的加速度还没有到零.运动过程中两物体的加速度不是同时为零,两物体不是同时达到最大速度,故系统静止时的平衡位置和运动过程中三个物体的瞬时平衡位置并不重合.那么,C物体在什么位置速度最大呢?

由系统机械能守恒ΔEp减＝ΔEk总,得

图8

为了深刻理解在运动过程中两物体的加速度不是同时为零,下面我们从物理的角度推导出C物体速度最大时角度θ满足的方程.

首先推导绳连接体关联加速度方程,这是解决上述问题的关键.

如图9 所示,假设A物体的加速度为aA,以向上为正方向;C物体的加速度为aC,以向下为正方向.将aC沿绳方向和垂直于绳方向正交分解,得C物体沿绳方向的加速度为

图9

同样将C物体的速度分解为沿绳方向的分速度v∥＝vCsinθ和垂直于绳方向的分速度v⊥＝vCcosθ,其中v∥使定滑轮右边绳子伸长,所以v∥＝vA,而v⊥使C物体随绳子绕定滑轮转动.下面分析这两个分速度变化在沿绳方向引起的加速度.

若只考虑C物体沿绳方向的运动,则C物体沿绳方向的加速度a1＝aA,方向背离定滑轮,此加速度是沿绳方向的分速度v∥的大小变化引起的;若只考虑C物体随绳子绕定滑轮的转动,则C物体沿绳方向的加速度,即C物体做圆周运动的向心加速度

方向指向定滑轮,此加速度是垂直于绳方向的分速度v⊥的方向变化引起的,故C物体沿绳方向的加速度

联立式②③得绳连接体关联加速度方程为

由式④可知,当C物体的加速度aC＝0时,C物体速度vC最大,但A物体的加速度0,此时绳子的拉力FT不等于A物体的重力mg,因此在运动过程中两物体的加速度不是同时为零,两物体不是同时达到最大速度.另外根据绳连接体关联加速度方程可知,对于绳或杆在转动的连接体,沿绳或杆方向的加速度分量并不相等,这与绳或杆连接体关联速度的特征有本质的不同.

对A物体,由牛顿第二定律得