基于PSO-OSSART 算法的非轴对称电弧发射系数重建质量评价

2022-09-14洪海涛王璐韩永全昌乐

焊接学报 2022年7期

洪海涛，王璐，韩永全，昌乐

(内蒙古工业大学,内蒙古自治区轻金属材料重点实验室,呼和浩特,010051)

0 序言

近年来，为了满足现代装备制造领域对焊接工艺高质量、高效率的要求，相继提出多种复合焊接技术[1-2].电弧作为能量传输的载体，可以采用温度场来描述其热力学状态.为了最大程度发挥复合焊接的优势，对电弧热力学状态进行研究，有助于了解电弧内在本质，进而改善焊接工艺，提高焊缝质量.

发射系数重建作为获得电弧温度场的关键环节，其重建质量直接关系到温度场的准确性.对于柱对称电弧，可以采用Abel 逆变换得到电弧不同位置的发射系数分布.而对于非对称分布的复合焊接电弧而言，如果光谱诊断时仍假设电弧呈对称分布，会极大的增加发射系数计算误差，降低电弧温度场的可靠程度.为此，研究人员提出多种非轴对称电弧发射系数重建算法计算发射系数[3].常用的三维重建算法有代数迭代重建算法、统计迭代重建算法以及压缩感知理论.代数重建算法作为典型的迭代重建算法，其基本思想是给离散化区域赋初值，从多个角度得到投影值，与累加谱线强度值比较并加以校正，直到满足所需要求后结束迭代过程.由于需要对射线进行逐条更新修正，重建速度慢，Liu 等人[4]利用联合迭代重建算法对同一投影角度下的所有射线误差进行累计，避免单条射线误差对重建结果的影响，可以有效抑制噪声信号.李慧君等人[5]提出两相式重建策略，先利用代数重建算法重建中间图像进行非负约束，再采用选择性全变差最小化对图像进行优化修正，循环执行上述运算直到重建结果满足收敛准则为止.然而，由于算法所需投影数量庞大，对焊接电弧投影数据完备性提出较高的要求[6].为了解决上述问题，研究人员提出收敛速度快，重建结果平滑的有序子集-联合重建算法(ordered subsets-simultaneous algebraic reconstruction technique,OSSART)，以期在电弧发射系数分布重建中得到应用.

采用OSSART 算法重建非轴对称电弧发射系数存在以下两方面的问题.首先，在电弧光谱诊断过程中，由于工况及成本等因素[7]，无法实现0°～180°范围内光谱数据的逐角度采集.对于这类角度稀疏重建问题，由于投影方程的数量远小于待求解未知数数量，导致目标函数求解呈现不适定性，采用迭代方式求解容易收敛至局部最优解，难以得到满意的重建质量.为了避免此类问题出现，可以借鉴随机优化算法的求解过程.随机优化的思路是当求得的解陷入局部最优解时，算法根据其独特的新样本产生机制，不仅能够保证解的多样性，更有利于获得全局最优解[8].除此之外，对于OSSART 算法，重建质量依赖于子集个数、松弛因子以及松弛因子衰减系数的合理设置.如果重建参数采用控制变量法逐一尝试的方式获得，难以兼顾参数间的交互作用，无法获得最佳的重建质量.

采用随机粒子群优化OSSART 算法，快速获取质量最优的重建参数组合.对模拟发射系数投影数据进行重建，采用归一化均方根误差对粒子群-有序子集-联合重建算法(particle swarm optimizationordered subsets simultaneous algebraic reconstruction technique,PSO-OSSART)和最大似然函数-期望值最大化算法(maximum likelihood expectation maximum,MLEM)发射系数稀疏角度重建质量进行评价，为非轴对称电弧可靠光谱诊断提供理论依据.

1 发射系数重建算法

针对焊接电弧角度稀疏的不完全投影数据，采用OSSART 和MLEM 两种迭代算法重建发射系数.MLEM 算法为统计迭代算法，其思路是将电弧截面离散为N个正方形网格，使M条平行射线从多个角度穿过网格得到投影pi(i=1,2,···,M)，对所有角度的投影数据进行校正，更新发射系数，其迭代式(1)[9]为

式中：εj为第j(j=1,2,···,N)个网格的发射系数；k为迭代次数；wij为投影系数.OSSART 算法为代数迭代算法，其思路和MLEM 算法类似，不同之处是将投影数据分成t个子集{S1,S2,···,ST}，依次使用每一子集内的投影数据校正更新发射系数，其迭代式(2)[10]为

式中：λ0为初始松弛因子；λr为松弛因子衰减系数.

对于OSSART 算法重建时需要合理设置投射角度间隔、子集数、松弛因子及其衰减系数才能实现准确重建.为了减少OSSART 算法因主观选取的不足，文中提出采用粒子群启发式随机优化算法[11]，通过种群间的协作和信息共享，依靠个体的最优值来寻找种群的最优值，使得种群向目标逼近，从而获得最优的重建参数组合.粒子群算法的速度、位置更新公式为

式中：Vn为第n个粒子的速度；k为迭代次数；wmax为最大惯性权重；wmin为最小惯性权重；kmax为最大迭代次数；c1，c2为学习因子；rand为(0,1)内的随机数；Pbestn为第n个粒子的历史最优解；Gbest为种群的最优解；Pn为第n个粒子的位置.为了平衡算法的全局搜索能力和计算量，粒子群算法参数设置如表1 所示.

表1 粒子群算法参数Table 1 Parameters for particle swarm optimization

2 模拟发射系数分布模型的建立

采用由CMOS 高速摄像机、带通滤波片以及中性滤波片组成的光谱信息采集系统得到变极性等离子-熔化极气体保护复合焊 (variable polarity plasma arc-metal inert gas welding,VPPA-MIG 复合焊)电弧Ar I 794.8 nm 的特征谱线图像，如图1 所示.

图1 VPPA-MIG 复合焊电弧特征谱线图像Fig.1 Characteristic spectrum image of VPPA-MIG hybrid welding arc

从图1 可以看出，电弧不同高度，特征谱线强度分布存在显著差异.对于复合电弧上半部分，仅存在等离子电弧，由于等离子电弧与MIG 焊电弧的电磁耦合作用[12]，等离子电弧中心轴线向左侧偏斜.图2 为不同电弧高度的谱线强度分布.图2a为等离子压缩喷嘴下方1 mm 截面处的特征谱线强度分布，谱线所在区域狭小并且电弧中心谱线强度有所降低.对于复合电弧下半部分，等离子电弧和MIG 电弧同时存在.图2b 为等离子压缩喷嘴下方9 mm 截面处的强度分布，谱线强度呈现双峰分布，两电弧结合区域出现较大幅度的强度降低.

图2 不同电弧高度的谱线强度分布Fig.2 Spectrum intensity distribution at different arc heights.(a) section of 1 mm below the nozzle;(b)section of 9 mm below the nozzle

结合上述复合电弧特征，采用二维高斯函数模型A 和模型B 模拟上述发射系数分布，其表达式分别为

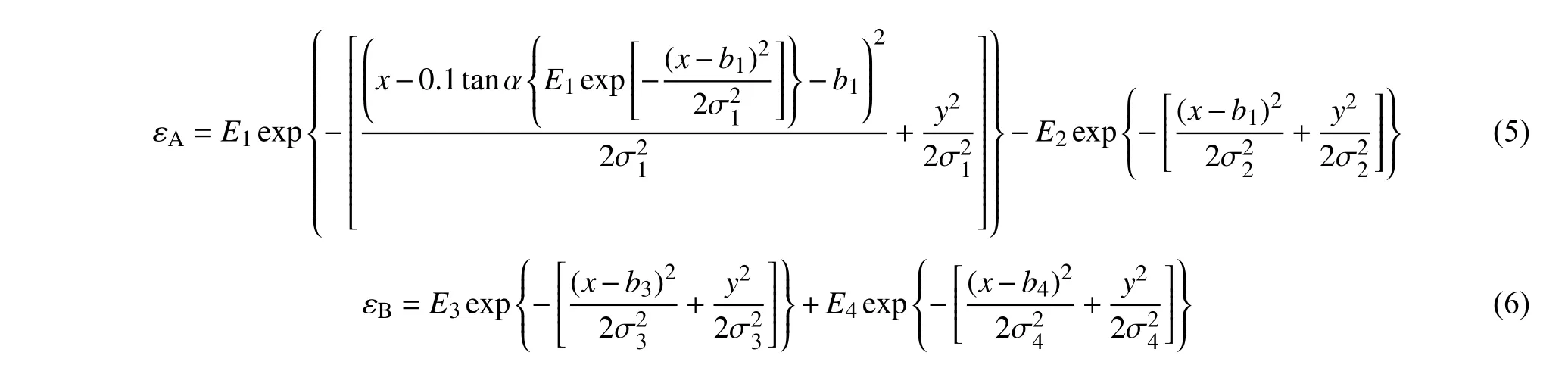
式中：εA和εB分别为模型A 和模型B 的发射系数；x为横坐标；y为纵坐标；E1,E2,E3,E4为模型A 和模型B 的发射系数分布曲线的幅值；b1,b3,b4为模型A 和模型B 的曲线中心；σ为模型A 和模型B 的标准差；α为电弧的偏斜角.分别对图2a 和图2b 数据进行高斯拟合，得到两种模型参数如表2 所示，其中α的取值为π/200.发射系数分布如图3 所示.

图3 模拟发射系数分布Fig.3 Distribution of simulated emission coefficients.(a) model A;(b) model B

表2 发射系数模型参数Table 2 Parameters of emission coefficient model

3 发射系数重建质量评价

在(0,180°)范围内，对经归一化的发射系数分布模型进行radon 变换，得到不同投射角度间隔情况下的特征谱线强度.采用归一化均方根误差δ评价重建质量，其表达式为[13]

式中：εjk为网格j第k次迭代的发射系数重建值；εj为发射系数的实际值.将重建区域离散为281 ×281 的网格，每个角度投影采样数为397，迭代次数为150.为了加快迭代收敛速度，采用Mueller 提出的加权距离最大方式[14]安排子集间投影访问顺序.以重建区域归一化均方根误差为适应度函数，采用粒子群算法对OSSART 算法重建参数进行优化，得到重建质量最优的参数组合，如表3 所示.

表3 OSSART 算法重建参数Table 3 Reconstructed parameters of OSSART algorithm

由于重建时无需额外设置参数，MLEM 算法不需要进行粒子群算法优化.文中采用两种方式评价算法重建质量.首先，以重建区域整体发射系数分布为对象，采用归一化均方根误差，评价算法重建质量，如图4 所示，图中圆圈表示重建误差的最小值.

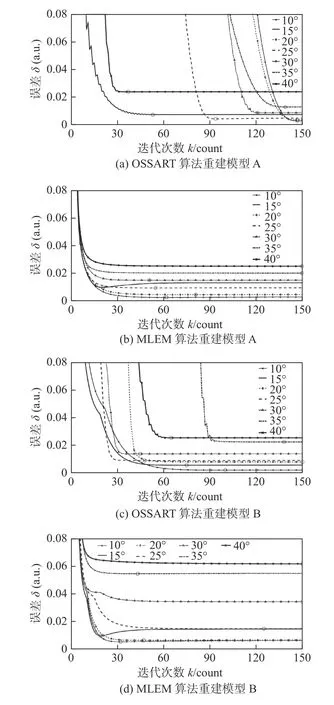
图4 迭代过程中重建误差的变化Fig.4 Changes in reconstructed error during iterations.(a) OSSART algorithm of reconstructed model A;(b) MLEM algorithm of reconstructed model A;(c)OSSART algorithm of reconstructed model B;(d)MLEM algorithm of reconstructed model B

从图4 可以看出，在投射角度间隔相同的条件下，采用OSSART 算法得到的重建误差明显低于MLEM 算法.重建算法误差对电弧截面发射系数分布的敏感程度不同.相比于仅存在等离子电弧，分布相对单一的模型A，分布更为复杂的复合电弧模型B 采用OSSART 算法在大投射角度间隔条件下能够获得更好的重建质量.当投射角度间隔小于25°时，OSSART 算法重建误差相比于MLEM 算法降低约35.3%，而当角度间隔大于25°时，OSSART算法重建误差降低约57.8%.

以发射系数分布中间行的数据为对象，对比不同投射角度间隔OSSART 算法和MLEM 算法的重建质量，如图5 和图6 所示，图中误差为重建发射系数与原始发射系数的差值.

图5 不同投射角度间隔下模型A 的发射系数分布中间行的重建质量Fig.5 Reconstructed quality of the emission distribution middle row of model A at different projection angle intervals.(a) projection angle interval 20°;(b) projection angle interval 30°;(c) projection angle interval 35°;(d) projection angle interval 40°

图6 不同投射角度间隔下模型B 的发射系数分布中间行的重建质量Fig.6 Reconstructed quality of the emission distribution middle row of model B at different projection angle intervals.(a) projection angle interval 20°;(b) projection angle interval 30°;(c) projection angle interval 35°;(d) projection angle interval 40°

对于电弧外围区域(模型A 为图中-1.25～-0.8 之外的区域)，两种算法在发射系数重建时均能达到较高的精度，而对于电弧中心区域，OSSART算法得到的重建结果边缘保持能力优于MLEM 算法.据测算，电弧中心区域流过的能量约占电弧整体传导能量的70%[15]，为了保证电弧物理研究的可靠性，该区域需要更高的重建精度.对于模型A，MLEM 算法需要投射角度间隔小于20°才能保证重建质量，当投射角度间隔增加为30°时电弧中心的发射系数已无原始数据的变化趋势.而OSSART算法，投射角度间隔为35°时还能基本保证重建质量.对于模型B，两种算法所需要的最低投射角度间隔相应提高.因此，为了保证VPPA-MIG 复合焊接电弧的重建质量，尽可能的减少特征谱线拍摄次数，应采用OSSART 算法在180°范围内投射角度间隔30°采集投影数据.