积分通用计划下零售商的联盟与利润分配
2022-09-13高举红王朋硕
高举红, 王朋硕
(天津大学 管理与经济学部,天津 300072)
0 引言
为了促进销量,越来越多的大型连锁商场、电影院等开始使用会员消费积分制。在这种消费积分制下,消费者进行消费可以获得积分,该积分可用于在下次消费时兑换商品或小礼品,这种方式受到了消费者的普遍欢迎。为了促进销售和提高消费者的忠诚度,留住老客户、吸引新客户,零售行业也都普遍实施了消费积分计划。
与此同时,多零售商间的联盟促成了会员消费积分通用计划(以下简称积分通用计划)。在这种合作模式下,消费者从一个零售商处购买商品可以获得积分,该积分可在联盟内的任意其他零售商处进行兑换。多零售商的联盟大体上可以分为两种,一种是异业联盟,另一种是同业联盟。异业联盟是指不同行业间商业主体的联合,他们之间只有合作,不存在竞争;同业联盟是指相同行业的商业主体的联合,他们之间既有合作,也存在竞争;需要注意的是,一方面,积分通用计划的引入给消费者兑换积分带来很大的灵活性,消费者有了更多的选择;另一方面,由于一个零售商无法决定联盟内其他零售商的积分转换比例(此比例决定了进行一次购买可获得的积分数量),因此该零售商创造的额外商品成本可能会部分由联盟内其他零售商承担,即一个零售商寻求自己的最大利润可能会导致其他成员付出代价,在这种情境下,多零售商间的联盟合作应该关注零售商的决策问题。
学术界对积分通用计划下的零售商联盟合作进行了大量研究。Matilda等对积分通用计划下的溢出效应进行了研究[1]。Cao等研究了联盟忠诚度中的奖励问题[2]。Salma等设计模型和框架,确定了积分计划的合理性和有效性[3~5]。Lu等表示对同一产品,消费者在零售商合作销售的模式下表现得更积极[6]。Ilkyeong等确立出积分转换机制,为研究积分的兑换提供了便利[7]。
利润分配是多零售商联盟中的一个重要而矛盾的问题,它对联盟下合作的持续稳定发展起着决定性的作用。Gérard等研究了收益共享契约的利弊,并将其与其他契约(回购契约、数量折扣契约、价格折扣契约等)进行比较,Ilkyeong等深入研究,提出了目标补偿合同,以协调两个零售商的利润[7,8]。李汉等从供应链成员、市场需求、成员博弈顺序、建模考虑顺序、合作后的利润分配方法5个角度对国内关于供应链利润分配的研究进行了总结[9]。李欧阳建立了第三方物流企业战略联盟的横向利润分配模型[10]。Chen等对夏普利值法进行修订,建立新的模型解决联盟企业间的利润分配问题[11,12]。Zhao等深入探讨了在收益共享契约的协调下,如何进行共谋和信息通用[13]。习怡衡等研究供应链合作伙伴关系的利益分配机制,实现了供应链合作伙伴关系收益分配的整体流程,并设计了利益分配的有效性评价指标体系以确保利益分配的公正[14]。
综上,本研究关注的问题如下:当联盟内零售商存在竞争时,(1)联盟内的零售商如何根据积分通用计划确定自己的积分转换比例与促销水平?(2)在积分通用计划下,如何协调零售商之间的利润?
1 问题描述与符号约定
本文以同业联盟为背景,考虑由两个竞争性零售商组成的横向供应链,两者进行联盟,实现积分通用,即消费者在零售商1处购买获得积分允许在零售商2处进行兑换。
符号约定如下:
ci:零售商i的单位产品采购价格(i=1,2);
pi:零售商i的单位产品销售价格(pi≥ci);
βi:一个期末在零售商i处的有效积分的比例(0≤βi≤1);
θi:消费者在零售商i处购买所获得的积分又在零售商i处进行兑换的比例(0≤θi≤1);
γi:零售商促销对销量的影响系数;
ε:两个零售商之间的竞争程度;
ηi:促销成本系数;
λi:零售商i的积分转换比例(当消费者从零售商i处购买1单位的产品时,可获得wipi的积分,有0≤λi≤1),为决策变量;
fi:零售商i的促销水平,为决策变量;
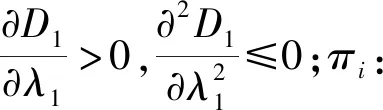
角标说明:
i:i=1表示零售商1;i=2表示零售商2;i=S表示整个联盟;
Ⅰ:表示联盟前的会员消费积分制;
Ⅱ:表示联盟后的积分通用计划;
Ⅲ:表示利润分配机制下联盟后的积分通用计划;
*:表示最优解;
C:表示集中决策。
同时,模型满足如下假设:
假设1消费者在进行积分兑换时,无需支付额外费用。
假设2考虑到积分的使用具有时效性,在一个时期内获得的积分,若在期末未进行兑换则积分作废。
假设3参考Moon I等[16]积分转换比例λi越大,则联盟前零售商i自己实施会员消费积分制的原有销量Ai越大,两者成线性函数,有A=ai+biλi(ai、bi为常数)。
假设4在[16]的基础上考虑积分的时效性,零售商之间进行联盟后各自会增加一定的销量,用Bi表示Bi=ξiln(βiλi+1),(ξi为大于0的常数)。
2 模型分析
2.1 分散决策下零售商积分联盟前的会员消费积分制
(1)
(2)
命题1在零售商联盟前的会员消费积分制下,可得到两个零售商的均衡解
(3)
(4)
(5)
(6)
2.2 分散决策下零售商积分联盟后的积分通用计划
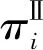
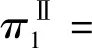
(7)
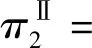
(8)
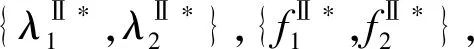
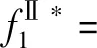
(9)
(10)
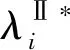
可以看出当兑换比例和有效积分比例增大时,零售商可以适当降低自己的积分转换比例来增加利润。
2.3 模型比较
命题4在分散决策下积分联盟后,积分通用计划零售商的促销水平的均衡解始终联盟零售商的促销水平的均衡解。所以零售商采用积分通用计划后需要加大促销力度来吸引消费者。
可以得到零售商i关于积分转换比例λi的边际净利润和边际积分成本见表1。

表1 零售商i的边际利润与边际积分成本
2.3.1 数值算例
为了看出边际利润和边际成本的变化,进行数值算例分析,假设c1=70,p1=100,a1=20,b1=200,β1=0.7,ξ1=100,γ1=5,ε=2,f1=3,f2=4,图1a和图1b显示了积分兑换比例在70%和90%时,零售商1的边际利润与边际积分成本的变化。
2.3.2 结论
(1)联盟后积分成本小于联盟前的积分成本,这也为零售商之间联盟提供了动机。
(2)与联盟前相比,零售商可以在联盟后适当调高积分转换比例。
(3)零售商在联盟之后可以适当降低积分转换比例,但该积分转换比例仍大于联盟前。
2.4 集中决策下零售商联盟后的积分通用计划
两个零售商的总利润表达如下:
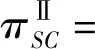
(p2-c2)D2-β2c2θ2λ2D2-
(11)
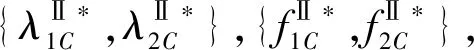
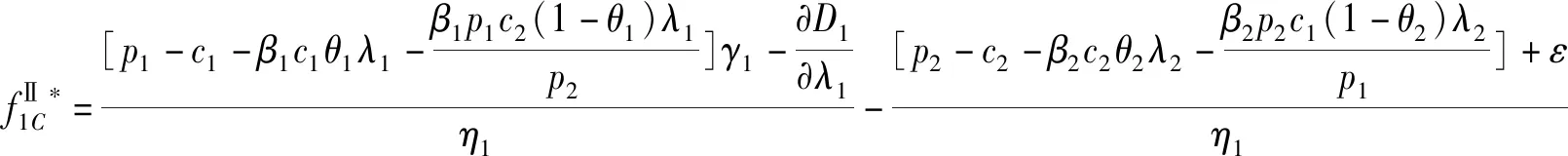
(12)
(13)
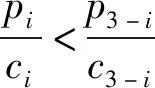
当某一零售商的商品价格与成本之比较高时,联盟通过引导消费者前往该零售商处进行兑换可以获得更高的联盟整体利润。
2.5 零售商联盟后积分通用计划下分散决策与集中决策的比较
2.5.1 数值算例
选取销量相差较大的两个零售商进行数值算例分析,可以更加直观地看出两个零售商联盟前后的利润变化,以帮助零售商和联盟整体做出合理决策。假设c1=70,p1=90,c2=80,p2=110,β1=80%,β2=85%,ξ1=30,ξ2=20,a1=1,a2=120,b1=10,b2=320,γ1=30,γ2=4,η1=35,η2=30,ε=3,则有:D1=1+10λ1+30ln(0.8λ1+1)+30f1-3f2,D2=120+320λ2+20ln(0.85λ2+1)+4f2-3f1,为了看出θi的变化对利润的影响,确定θ2=80%,分别选取小于、等于和大于θ2的5个不同的θ1值,表2和表3分别展示了在不同的θ1下,积分通用计划下分散决策与集中决策的利润对比。

表2 θ2=80%时,积分通用计划下分散决策的利润
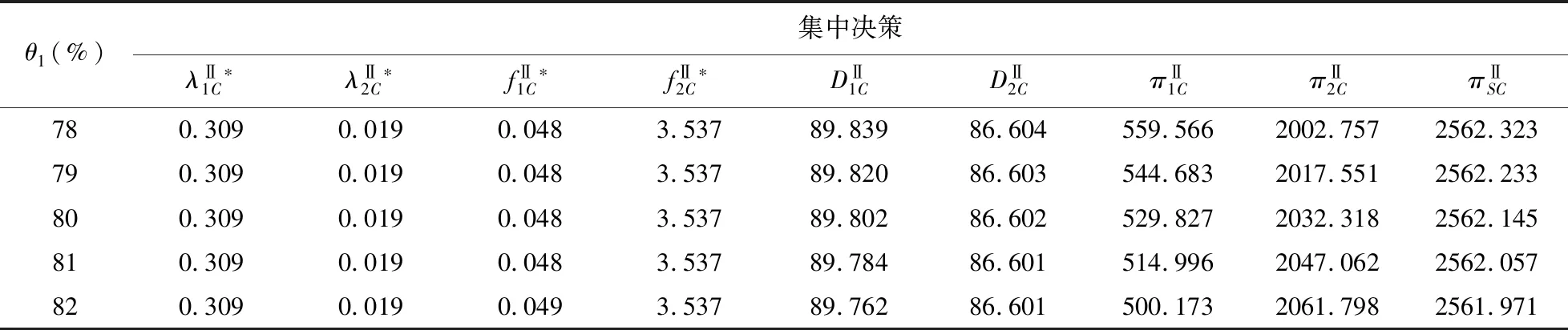
表3 θ2=80%时,积分通用计划下集中决策的利润
2.5.2 结论
3 利润分配机制研究
在积分通用计划的背景下,对于零售商来说,积分成本是一个很重要的概念,因此本部分使用积分成本共担的方法来解决零售商之间的总体利润分配问题,在该机制下,两个零售商经过讨价还价确定各自积分成本共担的比例φi,其中有0<φi<1,φ1+φ2=1。
在此机制下,两个零售商的利润可以表示为
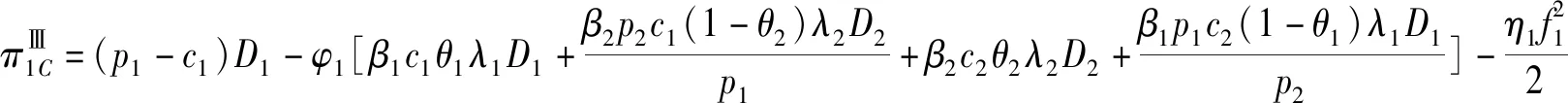
(14)
(15)
此时整个联盟的利润函数与集中决策一致表示为:
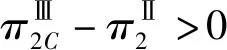
3.1 数值算例
假设c1=70,p1=90,c2=80,p2=110,β1=80%,β2=85%,ξ1=30,ξ2=20,θ1=82%,θ2=80%,a1=1,a2=120,b1=10,b2=320,γ1=30,γ2=4,η1=35,η2=30,ε=3。
由上述数据可以得出φmin,φmax,图2为在不同的积分成本共担比例下零售商的利润变化图。
3.2 结论
当零售商1分担的积分成本比例φ1位于区间(φmax,φmin)内时,与分散决策相比,两个零售商的利润均会增加,且在集中决策下联盟所增加的总利润可以在两个零售商之间任意分配,分配率依赖于参数φi,而φi的取值大小取决于联盟内双方的讨价还价能力,由表4可以看出,当φ1的值接近于φmin时,零售商1将分得更多的增加利润;当φ的值接近φmax时,零售商2将获得更多的增加利润。
4 结语
(1)联盟前后对比得出:虽然积分转换比例增大会带来更高的积分成本,但零售商在联盟后增大自己的积分转换比例,会获得比未联盟时更多的利润;由于联盟会给零售商带来额外的销量,因此零售商不必再增加促销成本以加大自己的促销力度来吸引消费者,即零售商可以在联盟后降低自己的促销水平。
(2)零售商进行联盟后:消费者若在某零售商处进行频繁的积分兑换,产生的积分成本更大,零售商适当降低自己的积分转换比例可以在联盟中获得更大的利润;在集中决策下,当零售商的售价与采购价之比更小时,消费者在该零售商处的兑换比例增大,则联盟总利润会随之减小;零售商在集中决策下的积分转换比例始终大于分散决策。
(3)为提高自己的利润,零售商更倾向于选择顾客量大的目标作为联盟伙伴,因此,联盟内成员只有销量相差不大,联盟才能更稳定,这为联盟间合作伙伴的选择提供了参考意见。
(4)在积分成本共担机制下,利润的分配依赖于成本共担比例,该比例取决于联盟之间成员的讨价还价能力,较强势的零售商分担成本的比例更小,将分得更多的利润。
