基于类内类间距离量级平衡的FCM聚类算法设计

江文奇, 牟华伟

(南京理工大学 经济管理学院,江苏 南京 210094)

0 引言

网络环境下数据与数据处理能力已经成为互联网企业的重要竞争力。近年来，第三方电子商务平台收集并存储了大量的客户购物和评价信息，通过实施客户聚类有效表征了不同类别客户的特征偏好，为精准营销提供了有力支撑。

聚类本质是将大量数据从空间上进行一种无监督无标号的划分，目的是挖掘数据的内在联系和潜在价值，已经广泛应用于模式识别、机器学习等领域[1]。模糊C均值(Fuzzy C-means, FCM)算法是一种常见且广泛应用的聚类算法，鲁棒性好且收敛性强。其中，初始聚类中心点、每个数据点与聚类中心点的隶属度、聚类模型设计等是FCM算法的核心内容[2]。

现有FCM聚类算法研究均突出了聚类稳定性特征。如文献[3]引入多维数据的邻域信息改进聚类算法，增加异常值和噪声点的稳健性。文献[4]根据数据之间互为K近邻关系来确定数据中的自然簇，减少算法对聚类参数的依赖程度。文献[5]提出基于全部最小连通支配集的聚类算法解决了算法易于陷入局部最小值的缺陷。多维大数据环境下，文献[6]结合灰狼算法和最大熵理论删减属性；文献[7]采用折线模糊数描述待聚类对象的指标信息并设计聚类算法；文献[8]提出了一种自适应特征熵权的FCM算法分析属性权重对聚类算法的影响程度；文献[9]将偏好矢量相聚度作为邻域相似度，构建启发式聚类算法解决多属性复杂大群体聚类与决策问题。

上述文献注重FCM算法的稳定性问题，但忽视了FCM目标函数对于聚类绩效的影响。通常，聚类模型与算法设计的有效性部分受制于目标函数，而目标函数中类内类间距离合成形式是关键点。于是，本文拟深入分析类内距离和类间距离之间的关系，基于两类距离数值量级的差异性，设计两类距离平衡方法，进而提出一种新的FCM聚类目标函数设计和聚类算法，提高多维大数据环境下FCM算法的聚类绩效。

1 FCM聚类算法概述

FCM聚类算法是一种应用广泛的聚类算法，其原理是基于数据属性的相似性以及数据属性的差异性，通过自动迭代算法实现对大量数据的聚类划分。假定聚类数据量为n(X=(x1,x2,…,xn)∈RS)，数据集维度为s，聚类中心点数为c，vi为第个聚类中心点，uij为样本点j对第i个类的隶属度(隶属度矩阵为U)，dij为样本点j对第i个聚类中心点的距离，模糊加权数m∈[1,∞)。经典FCM算法的优化模型为:

(1)

运用Lagrange乘子法求解，有:

(2)

其中，1≤i≤c,1≤j≤n。

FCM算法具体步骤描述为:

首先：确定聚类中心点个数c，模糊权重值m，初始聚类中心点vi。给定判断两次目标函数值大小之差或者目标函数迭代终止阈值β。

其次：依据式(2)求隶属度矩阵和新的聚类中心点，由式(1)求得目标函数值。

最后：计算前后两次目标函数值之差与β的大小关系(或目标函数值与β的大小关系)。若两次目标函数之值小于β值，则输出聚类中心点和隶属度矩阵，否则，重复步骤(2)。

2 FCM中类内与类间距离关系研究

针对经典的FCM聚类模型，以SFA和SFE迹表示类内和类间距离，有:

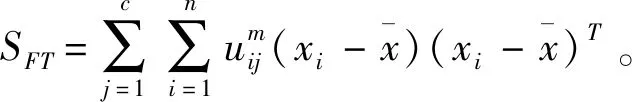
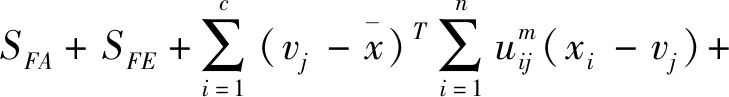
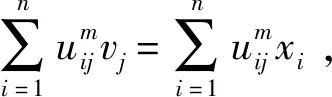
tr(SFT)=tr(SFA)+tr(SFE)

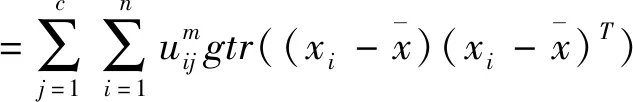
其中：tr(SFA)是经典FCM目标函数JFCM，tr(SFE)可作为具有隶属度加权类间距离测度，tr(SFF)为仅依赖于隶属度的不确定值。

为了平衡FCM聚类算法的类内类间距离，实现聚类过程中类内类间距离的有效融合，当前FCM聚类算法模型优化主要有以下几种方式：(1)添加惩罚函数项，动态调整类内类间距离差距；(2)增加权重系数平衡类类内类间距离；(3)结合熵函数表征类间离散程度、(4)基于核函数改变类内类间距离度量方式。结合tr(SFT)表达式，分析FCM聚类目标函数的类内类间距离关系。

(1)文献[10]结合竞争学习思想，在目标函数中添加惩罚函数项，目标函数表示为:

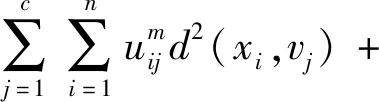
惩罚函数项为:

在tr(SFT)=tr(SFA)+tr(SFE)两侧添加加惩罚函数项可得:

等式右端为文献[10]类内距离目标函数值和类间距离之和，左侧值:

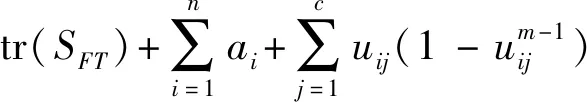
J(U,V)+tr(SFE)受到隶属度函数以及ai影响，不能确定min(tr(SFA))与max(tr(SFE))变化的一致性，即在确定类内距离最小化的同时不能保证类间距离最大化。

(2)文献[11]基于群体排斥思路添加惩罚项改进FCM聚类算法，目标函数为:

tr(SFT)=tr(SFA)+tr(SFE)左右加惩罚项，有:

等式右端为类内距离优化与类间分离度的和，左侧值：

因此算法没能有效实现类内距离最小化与类间距离最大化的融合。

文献[10,11]设置隶属度函数作为惩罚项，虽然降低了总体离差tr(SFT)对uij依赖程度，但没有实现JFCM最小化时tr(SFE)最大化有效融合。

(3)文献[12]基于高斯函数设置距离测度，并增加惩罚项以解决类内类间距离的融合问题。

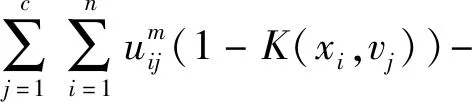
目标函数改进了tr(SFE)，对某样本点有:

若保证0≤uij≤1，则必有:

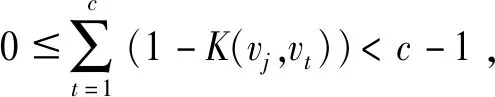
使得类间距离收缩到(0,1)范围内，在量级上与类内距离差距较大，不利于实现不同类的划分。

(4)文献[6]在兼顾类内距离与类间距离的基础上，提出改进型距离测度，其目标函数为:

文献[12,6]基于min(tr(SFA)-tr(SFE))思想，融合类内类间距离，理论上能够实现类内紧凑度与类间分离度同步最优化，但不同量级的类内类间距离差异大，会导致聚类效果不佳。

(5)文献[13]在目标函数中引入了聚类中心距离惩罚项，将类间距离分离度融合到目标函数，有:

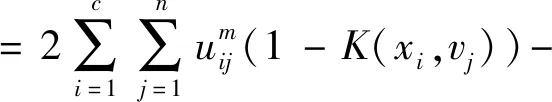
(6)文献[14]在目标函数中增添了最大中心间隔项与缩放因子η，避免了聚类中心趋于一致性。

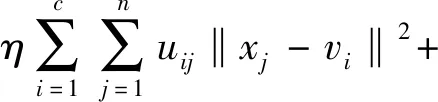
虽然文献[13,14]在类内类间融合上提出了创新算法，但没有有效解决类内类间距离的差异性对FCM聚类的影响。

上述类内与类间距离融合优化并不能有效实现类内距离最小化与类间距离最大化一致性变化，即聚类算法实现类内距离最小化的迭代过程，类间距离不能同步实现最大化。

3 FCM改进聚类算法设计

为了解决FCM聚类目标函数中类内距离和类间距离合成难的问题，实现类内距离最小化且类间距离最大化的聚类目标，本文将基于min(tr(SFA)-tr(SFE))的思想来设计FCM目标函数，借助高斯核函数距离测度改进目标函数相似性函数，统一类内类间距离的合成基础。

类内距离和类间距离的差异可以表示为:

tr(SFA)-tr(SFE)=JFCM-tr(SFE)

采用高斯核函数将特征空间X映射到H来替代欧式距离，又K(x,x)=1，映射过程为:

d(x,y)=‖Φ(x)-Φ(y)‖2

=(K(x,x)+K(y,y)-2gK(x,y))

=2(1-K(x,y))

高斯核函数对类内类间距离进行改进:

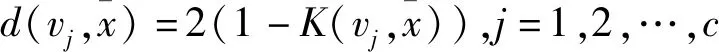
为了更好体现类内距离与类间距离在目标函数中的影响，实现类内类间距离的有效比较，K(x,y)为exp(-‖x-y‖2)/σ2)，0≤K(x,y)≤1。基于高斯核函数的距离测度，d(xi,vj)∈(0,2)，d(vj,vk)∈(0,2)，保证了类内与类间距离在距离范围上的一致性，提供了类内与类间距离融合的基础。

对类内与类间距离融合作如下设计：

改进的类内类间融合公式保证了类内与类间距离非负性且值在区间(-2+2θ,2+2θ)内，θ∈(0,1)为调控因子，平衡了类内与类间距离的量级，确保了算法收敛性，区间上限提高了聚类算法的精确度。

令m控制分类的模糊程度，值越大表明模糊程度越高，σ2是给定数据方差。改进型FCM聚类模型表示为:

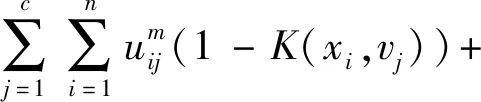
(3)

利用拉格朗日乘子法建立无约束优化目标函数:

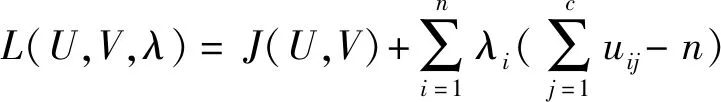
(4)

(5)

(6)

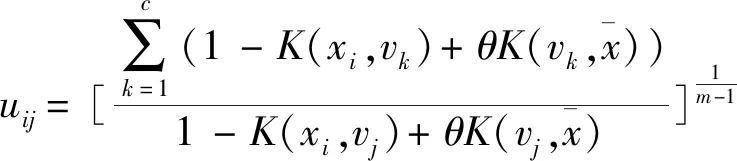
(7)

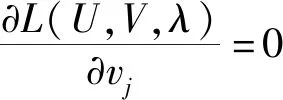
(8)

于是，改进的FCM聚类算法步骤表示为：

步骤1设定聚类个数、选取合适初始聚类中心点、模糊参数m、核函数参数σ、收敛精度ε、调控因子初始化为1/c、初始化迭代次数k=0；

步骤2依据式(5)计算各代表点隶属度uij；

步骤3根据式(8)计算vj，令k=k+1；

步骤4若‖Uk+1-Uk‖≤ε，停止迭代，否则转到步骤2；

步骤5输出隶属度矩阵U，聚类中心矩阵V。

4 算例研究

某企业为了设计针对学生人群的产品营销计划，选取了价格满意度、服务水平、物流速度三个评价指标，随机调查了南京地区600名学生客户(通过问卷星发放并收集问卷，本文作者负责设计与分析问卷)，通过实施客户聚类实现精准营销。取m=2，θ=0.02，σ2=6，迭代终止条件cpsm=10-6。聚类中心点矩阵为:

图1展示了本文提出的改进型FCM聚类算法的收敛过程，算法在5次迭代计算后开始收敛。图2为算法收敛后所有样本点的隶属度值，表现了样本数据点对每一类的归属程度。

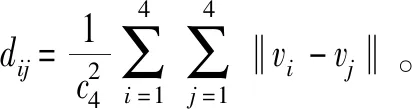
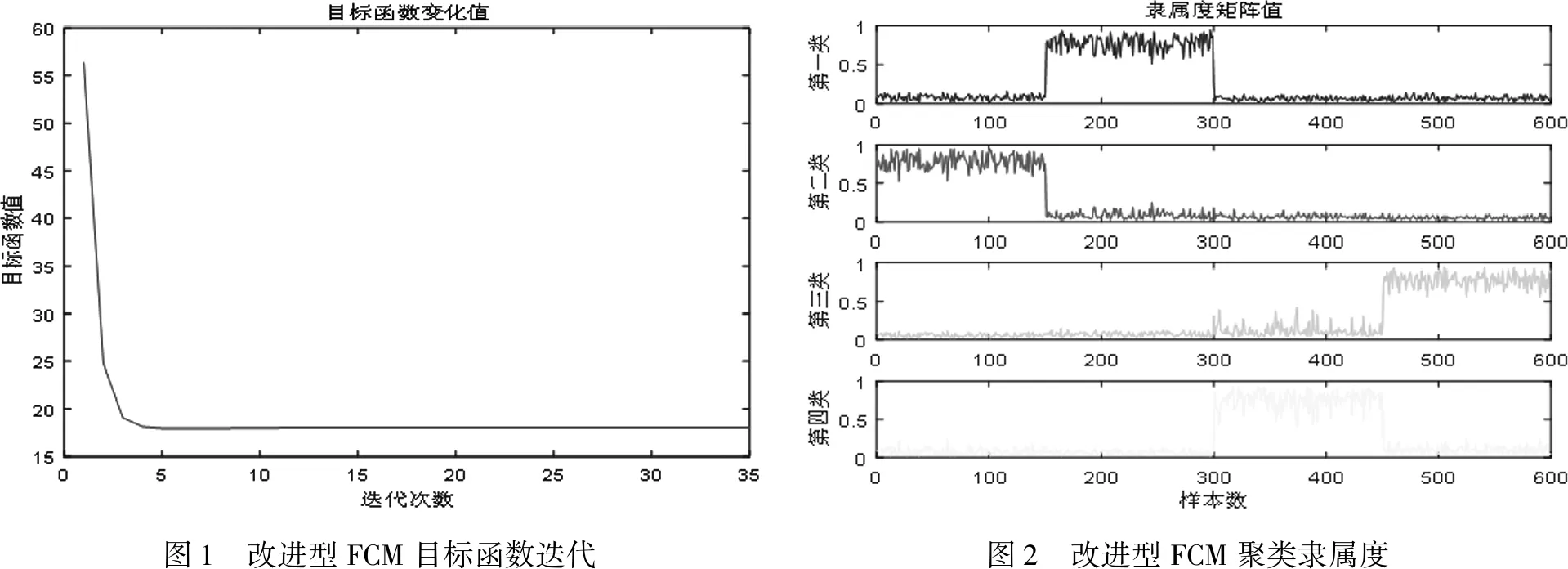
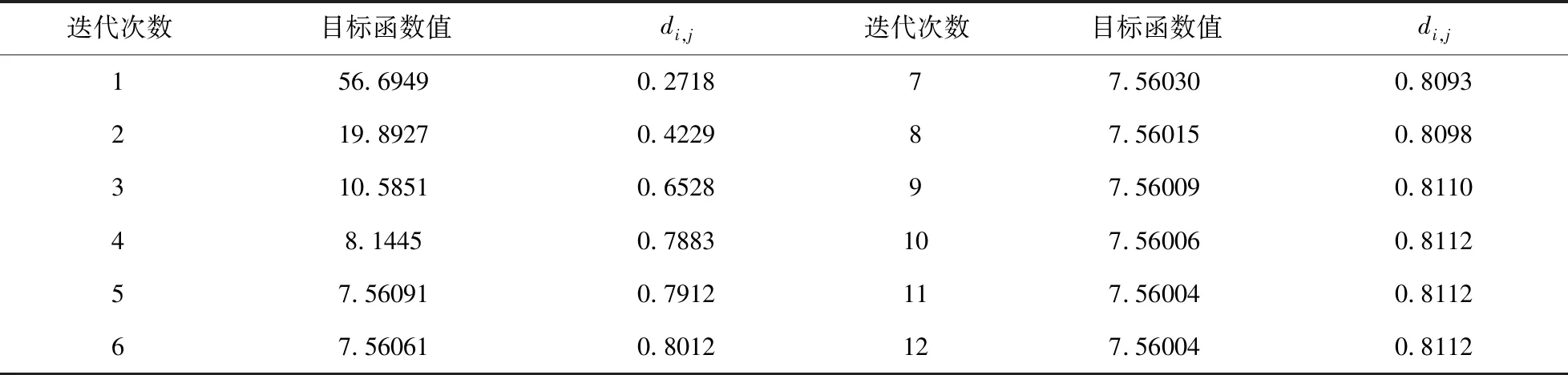
表1 改进型FCM类间距离变化

采用经典FCM算法进行样本点聚类时，取模糊参数m=2，epsm=10-6，聚类中心点矩阵为:

经典FCM算法9次迭代后开始收敛，收敛曲线如图3所示。图4为经典算法迭代收敛后所有样本点的隶属度值。

经典FCM聚类目标函数与类间距离变化值如表2。

比较图1和图4收敛曲线：改进型FCM聚类算法5次迭代计算便开始收敛，经典的FCM算法在第8次迭代计算才开始收敛，改进型FCM算法能够以更少的迭代次数实现算法的收敛，同时改进型FCM聚类算法的收敛曲线更加平滑，算法的稳定度更高。

通过对表1数据分析，随着改进型FCM聚类算法目标函数值的减小，类间距离di,j不断地增大，在目标函数值最小时类间距离达到最大。表2数据显示，经典FCM聚类算法在前5次迭代过程中，类间距离di,j不断增大，第5次迭代后，di,j随着目标函数值的变小呈现出先增大后减小的趋势，第8次迭代类间距离达到最大值，而目标函数值并未达到最小值，说明改进型聚类算法能够有效的实现类内距离最小化与类间距离最大化的一致性变化。

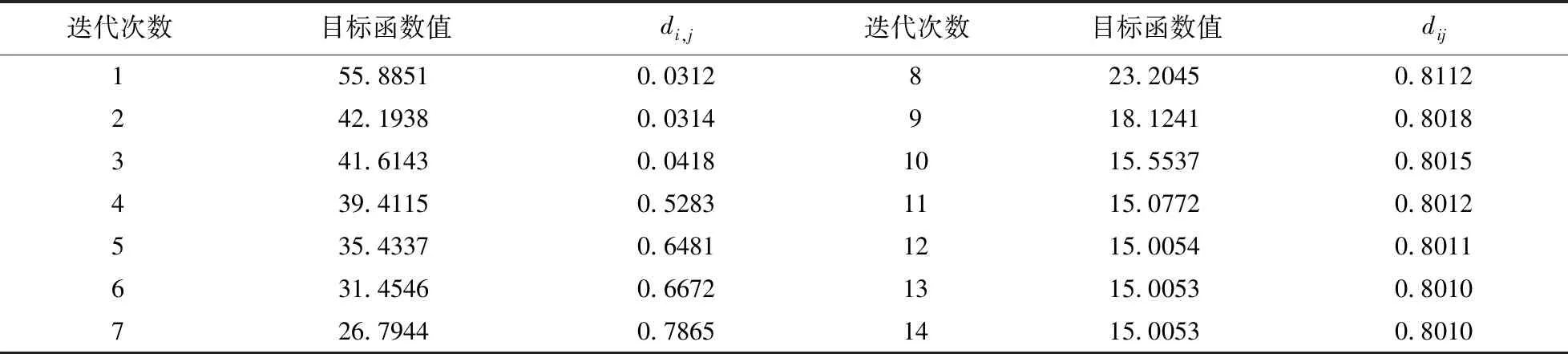
表2 经典FCM类间距离变化

为了进一步验证本文提出的改进算法可行性和有效性，采用国际上的标准测试数据UCI标准数据集Iris、Wine、Glass样本数据。

由表3可知，在维度方面Wine>Glass>Iris，分类方面则Glass>Wine=Iris。综合分类以及量级差异性程度，Glass>Wine>Iris。

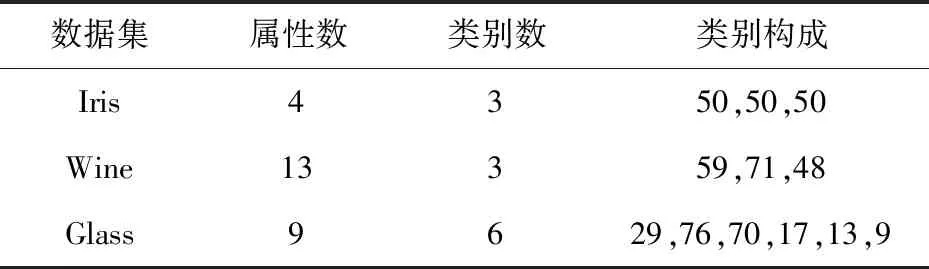
表3 实验数据集

采用Windows7，Matlab编程环境，分别以经典FCM聚类算法、KFCM聚类算法、本文提出改进FCM算法流程对三类数据进行聚类效果统计。得到表4。

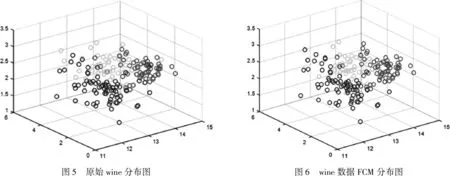
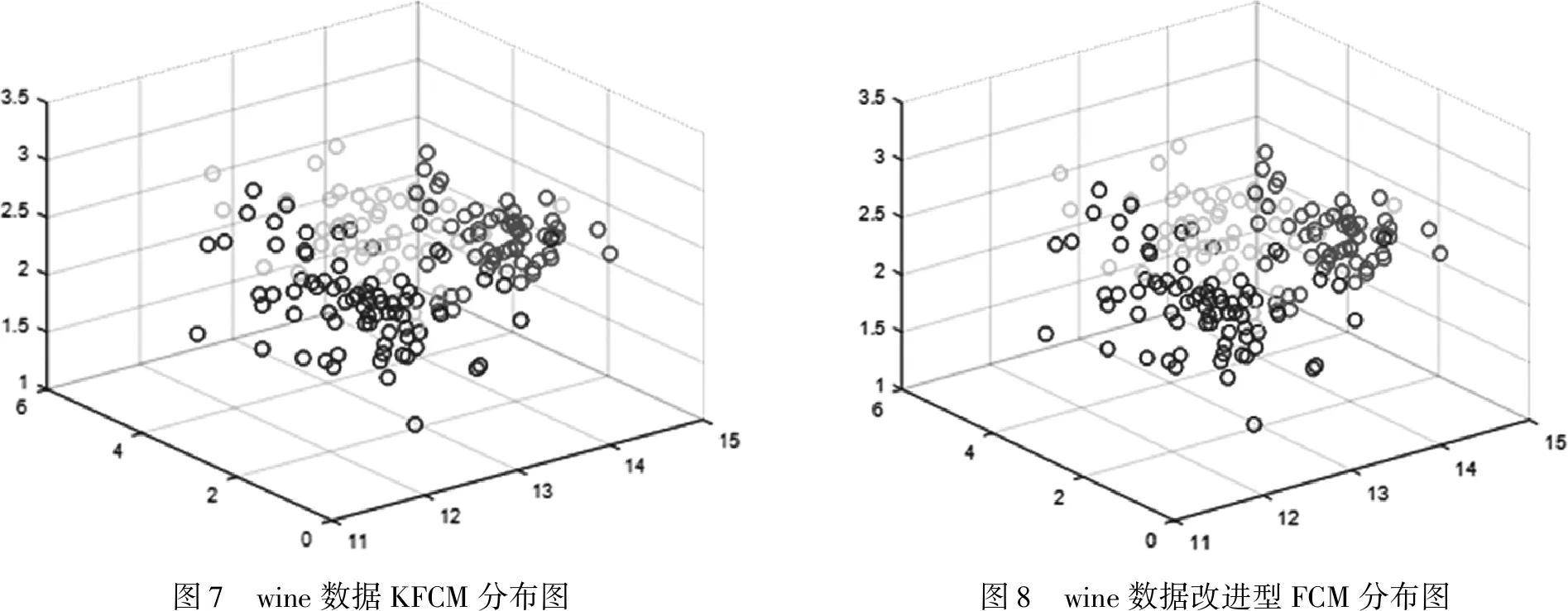
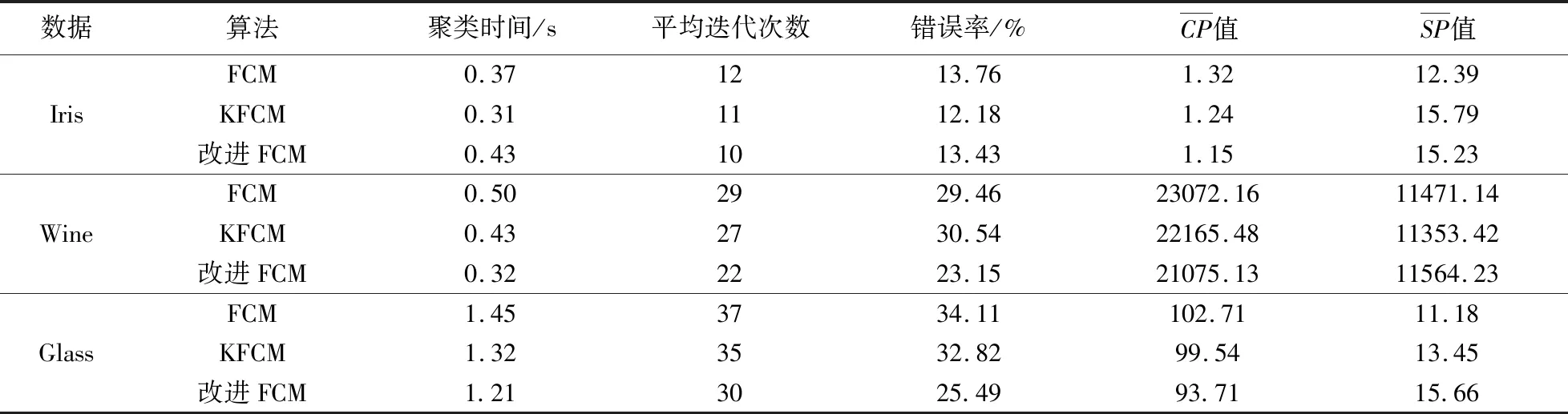
表4 聚类算法迭代效果

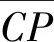
Compactness(紧密性)(CP):

Separation(间隔性)(SP)：

由上表可知在Iris数据集中，本文提出算法较其他算法处于平均水平，没有较为明显的优势；分类数不变，量级出现偏差的高维数据集中，改进算法在除聚类时间外的聚类效果表现中有一定的优势；而在量级差异较大且类簇更多的Glass数据总体来看，本文提出的改进算法平均迭代次数相比于其他的算法在逐渐减小，说明随着数据量级的差异变大以及类内类间距离的差异性增加，本文改进算法能够提高聚类效率。

算法计算时间方面，改进型聚类算法的时间复杂度为o(nkc)，与KFCM以及经典FCM算法相同。实际耗费时间上，对量级差异性不大的数据集，改进型FCM的算法复杂导致效率不高，耗时较长，但是对量级差异较大的数据集，改进行算法的迭代次数减少，时间降低。

结合改进型算法的聚类结果，类与类间的区别更为明显，可将调查学生群体划分为四类，即高消费人群、中等消费人群、服务主导型人群、普通型消费人群。针对不同的消费人群制定针对性的营销策略，例如，可以对高消费人群推送奢侈商品广告，对服务主导型人群可以推送服务型、提高生活质量的商品广告。

5 结论

不同量级数据聚类中聚类数据点的数量巨大，易造成聚类过程类内与类间距离的影响差异较大的缺陷，从而导致FCM聚类算法不敏感。针对聚类过程中目标函数没有有效地平衡类内与类间距离的问题，本文首先基于矩阵分解方式对类内与类间距离的关系进行分析，基于高斯核函数对类内与类间距离进行了融合，平衡类内与类间的影响。算例表明，改进的FCM聚类算法在处理大数据集的聚类过程中具有很好的收敛性以及鲁棒性，但在处理小数据量以及类间距离效果不明显，适用于处理类内与类间距离差较大的情况。