基于类间区分度的属性约简方法*

饶 亚，贾修一,,+，李同军，商 琳

1.南京理工大学 计算机科学与工程学院，南京 210094

2.浙江海洋大学 浙江省海洋大数据挖掘与应用重点实验室，浙江 舟山 316022

3.南京大学 计算机软件新技术国家重点实验室，南京 210093

1 引言

粗糙集理论[1-2]是一种有效地处理模糊及不确定知识的数学工具，在数据挖掘、知识发现等方面均有着重要作用。属性约简是粗糙集模型中一个关键性问题，所谓属性约简，就是寻找满足某种特定标准的属性最小子集的过程[3-4]。利用属性约简，能够有效地消除无关和冗余信息，减少属性数目，提高数据挖掘任务的效率，简化分析数据并提取数据中的关键信息[5-6]。

近年来，粗糙集理论模型中的属性约简问题引发了学者们广泛的关注与研究。许多学者提出了基于熵（包括信息熵[7]、互信息[8]、条件熵[9]等）、一致性[10-11]以及决策域[12-13]（包括正域、负域、边界域）等的属性约简定义。然而，这些属性约简定义大部分都是基于不可分辨或可分辨关系[14]所提出的，通过对具有等价关系的类簇对象的计算，来判定当前约简子集的表现性能的好坏，却忽略了不具有等价关系的不同类簇对象间关系的变化情况，而这些被忽略的类簇对象间的关系同样是影响约简子集表现性能的关键性因素之一。

针对该问题，本文提出了一种类间区分度的概念，用于衡量不同类簇对象间的区分关系，在其值的计算过程中需要考虑不同类簇对象间的关系及分布情况。相较于等价类和上下近似集而言，类间区分度考虑到了上述所忽略的不存在不可分辨关系的各类簇对象的区分关系情况，且其值的变化能够反映随着属性集的变化不同类簇间区分情况的变化。

本文基于类间区分度，定义了一种属性约简，并提出了相应的属性约简算法。在该方法中，将类间区分度的概念引入到属性约简中，在约简过程中充分考虑到该区分度值的变化情况，并给出类间重合度和类间区分度的概念以求解当前对象集各类簇间可分性大小。之后，基于所提出的属性约简定义并结合启发式搜索策略[15]提出了一种保持类间区分度值不变的属性约简方法，并通过一系列实验验证了所提约简方法的有效性。

2 类间区分度

本章将对类间区分度的相关概念进行介绍。

2.1 决策信息系统

粗糙集理论模型主要针对决策信息系统进行研究，一个决策信息系统可以定义为一个四元组DS=(U,A=C⋃D,V={Va|a∈A},f={fa|a∈A})且C⋂D=∅。其中，U表示一个有限非空对象集，A是一个有限非空属性集，C是条件属性集，D是决策属性集。V是非空值集且Va表示属性a的取值范围。f是一个信息函数，fa(x)表示对象x在属性a上的取值。且该决策信息系统可以简写为DS=(U,C⋃D)。对于给定的决策信息系统，对象集U能由决策属性集D划分为多个类簇，其表示为：U D={D1,D2,…,DM}(M＞0)，其中Di(1≤i≤M)表示对象集U的第i个类簇。此外，设条件属性子集R⊆C。

2.2 重合度

类间重合度是评价对象集U由决策属性集D划分的多个类簇中任意两类簇间对象重合程度的指标。

定义1（类间重合度）在决策信息系统DS=(U,C⋃D)中，对于由决策属性集D划分的任意两个类簇Di和Dj，设两类簇在属性子集R⊆C下的类间重合度值为InterCR(Di,Dj)，则其计算如下：

其中，Dik表示类簇Di的第k个对象，表示集合的基（即集合中元素的数目）。IR(x,Di)是与对象x和类簇Di有关的指示函数，定义如下：

其中，fR(x)={ }fa(x)|a∈R是决策信息系统中与对象x有关的信息函数。

例1如表1，DS=(U,C⋃D)是一个决策信息系统，U={o1,o2,…,o9},C={c1,c2,…,c5}且U D={D1,D2,D3}，其中D1={o1,o2},D2={o3,o4,o5},D3={o6,o7,o8,o9}。根据定义1，对于类簇D1、D2和D3，存在重合度值计算如下：InterCC(D1,D2)=0，InterCC(D1,D3)=1/3，即在条件属性集C下，类簇D1与D3的类间重合度大于类簇D1与D2的重合度。

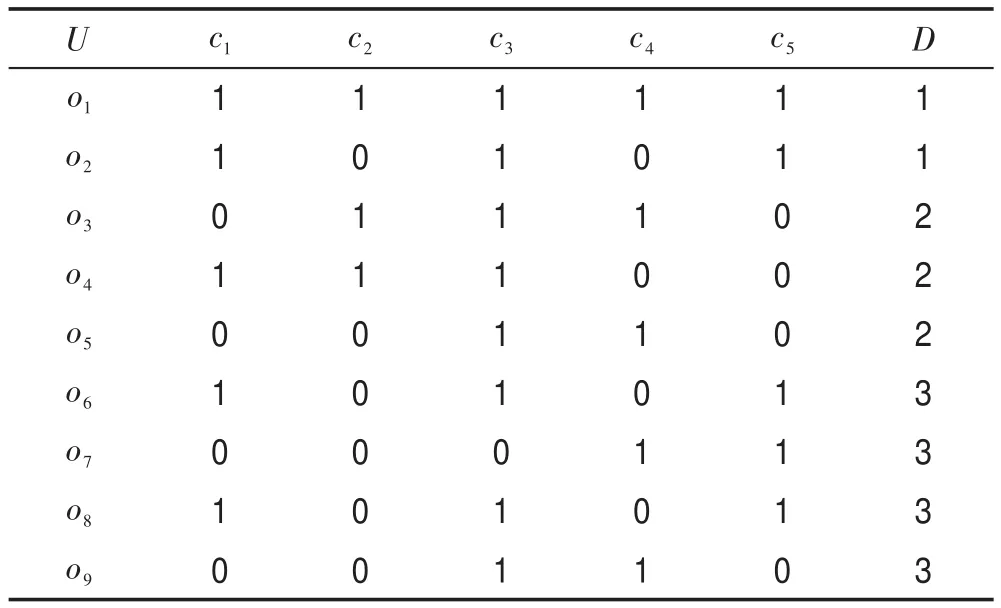
Table 1 Decision information table表1 一个决策信息表

2.3 区分度

与类间重合度相反，类间区分度是衡量对象集由决策属性集划分的多个类簇中任意两类簇间能被有效区分的程度值，也是两类簇间对象不重合的程度指标。在本节中，将对类间区分度的相关概念进行介绍。

定义2（类间区分度）在决策信息系统DS=(U,C⋃D)中，设InterSR(Di,Dj)是类簇Di和Dj间的区分度，基于类间区分度定义，则有：

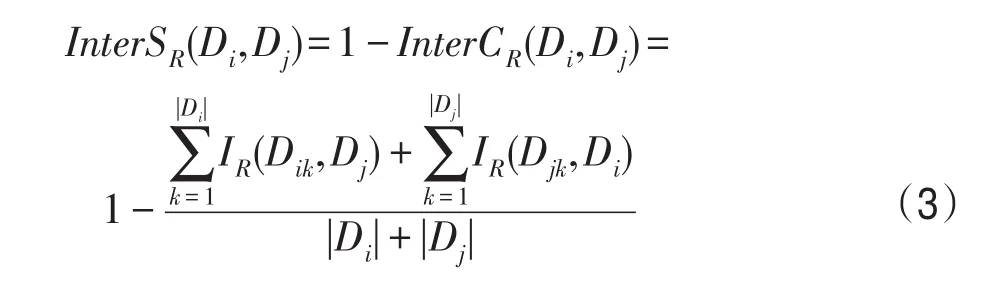
其中，随着InterSR(Di,Dj)值的增大，类簇Di和Dj间的区分度值越高，当前属性子集R下对类簇Di和Dj进行分簇操作时所产生的划分误差越小。

在本文中，提出全局类间区分度的概念，用以衡量当前对象集各类簇间区分度总值，以确定当前对象集分簇能力的大小。

定义3（全局类间区分度）在决策信息系统DS=(U,C⋃D)中，InterSR(Di,Dj)是对象集由决策属性集D划分的多个类簇中任意两类簇Di和Dj在条件属性子集R下的类间区分度。设InterSU(R,D)是对象集的全局类间区分度，则：

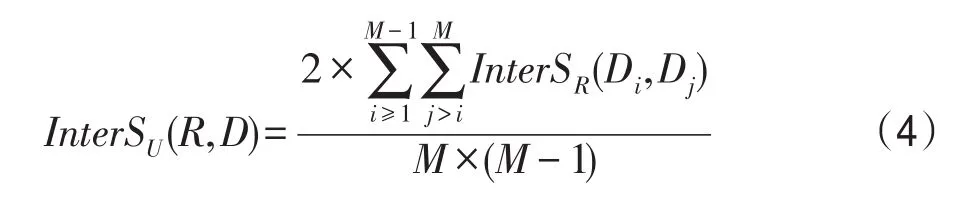
其中，InterSU(R,D)的值越大，表示在属性子集R下由决策属性集D划分的多个类间区分度的全局均值越大，对当前数据集进行分簇操作时的效果越好（划分错误率越低）。

定义4（基于全局类间区分度的属性重要度）R⊆C，在决策信息系统DS=(U,C⋃D)中，对于任意一个条件属性a∈R，条件属性a在属性子集R下基于全局类间区分度的属性重要度计算如下：

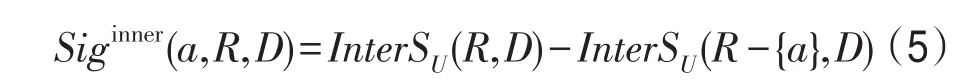
其中，Siginner(a,R,D)值越大表示该值所对应的属性a对类间区分度的影响越显著。

性质1在决策信息系统DS=(U,C⋃D)中，R⊆C且R≠∅，则有InterSU(C,D)≥InterSU(R,D)。

证明假设C={c1,c2,…,cn}且R={c1,c2,…,cn-1}，其中C⋂R=R，C-R={cn}。据上述定义，条件属性集C和R下对象集的全局类间区分度值计算如下：

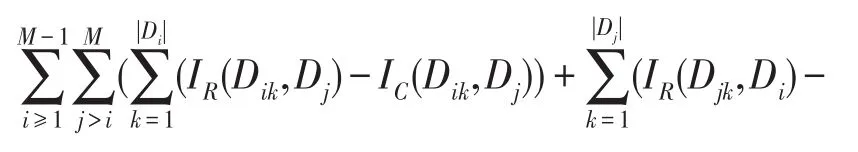
（1）假设fcn(Dik)=fcn(Djk)，则在删除属性cn时，对象Dik和Djk间关系不会改变，即IR(Dik,Dj)-IC(Dik,Dj)=0。

（2）假设fcn(Dik)≠fcn(Djk)，则Dik≠Djk（即IC(Dik,Djk)=0）。若删除属性cn，则有Dik=Djk或Dik≠Djk（即IR(Dik,Dj)=1或IR(Dik,Dj)=0），则IR(Dik,Dj)-IC(Dik,Dj)≥0。

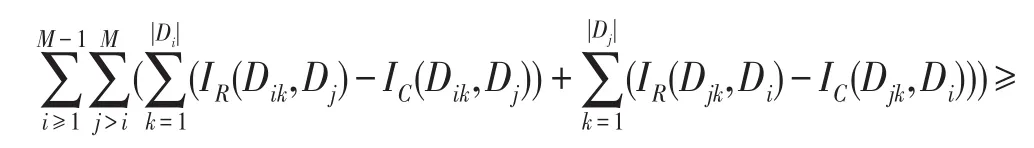
3 一种基于类间区分度的属性约简方法

作为影响对象集类簇划分能力的关键因素，应在属性约简过程中充分考虑到类间区分度值的变化情况。在本章中，基于类间区分度的定义和性质，定义了相应的属性约简，并提出了一种属性约简方法。

3.1 基于类间区分度的属性约简定义

通常来讲，使用属性约简的一个目的是期望能在更低划分错误的情况下进行类簇划分，而类间区分度就是影响各类簇间划分表现性能的关键因素。由前文可知，对象集各类簇的类间区分度值越大，对该对象集进行分簇操作时可能产生的分簇错误越少，且随着属性子集R中属性的减少，对象集U的全局类间区分度值会单调减小。在本节中，基于类间区分度的定义及其性质提出了保持类间区分度值不变的属性约简定义。

定义5在决策信息系统DS=(U,C⋃D)中，当且仅当条件属性子集R⊆C满足以下条件时，R是基于类间区分度不变的一个属性约简：

（1）InterSU(C,D)=InterSU(R,D)

（2）∀a∈R,InterSU(R-{a},D)＜InterSU(R,D)

在上述定义中，本文的目的是寻找一个属性子集R以在减少属性数目的条件下保持对象集U全局类间区分度的值不变。其中，条件（1）用以保证所获得的条件属性子集能够保持类间区分度值大小不变；条件（2）是确保所获得的约简是满足条件（1）的不含冗余属性的最小属性子集。

3.2 一种基于类间区分度的属性约简方法

根据上述基于类间区分度值不变的属性约简定义，提出了一种基于启发式搜索策略的属性约简方法。

首先，基于类间区分度和属性重要度定义，对条件属性集中各属性的重要度进行计算并排序。之后，基于属性重要度序列以及保持类间区分度值不变的约简定义，结合启发式搜索删除策略逐个删除属性重要度为零的属性，并利用区分度不变策略删除约简子集中的冗余属性，其具体操作流程见算法1。

算法1基于类间区分度不变的属性约简方法

输入：决策信息系统DS=(U,C⋃D)。

输出：约简子集R。

1.初始化：C→R。

2.对于属性子集R中的每一个属性ai计算其属性重要度：Siginner(ai,R,D)。

3.据属性重要度对R中属性进行排序。

4.删除属性重要度为零的属性：

约简循环1，选择R中属性重要度为零的属性ak：

①若InterSU(R-ak,D)=InterSU(R,D)，则{R-ak}→R；返回步骤4重复循环；

②若InterSU(R-ak,D)≠InterSU(R,D)，则跳至步骤5结束循环1。

5.删除约简集中的冗余属性ak：

for eachk=1 tok=|R|：

①计算InterSU(R-ak,D)；

②若InterSU(R-ak,D)=InterSU(R,D)，则{R-ak}→R。

6.返回R即为所求属性约简。

4 实验

为验证本文所提方法的有效性，在UCI数据库中的一些数据集进行实验。其数据集基本信息在表2中列出，其中列“Number of attributes”指条件属性集所包含的属性数目，“Size”指对象集所包含的对象数目，“Classes”表示决策属性所包含的不同取值数目。

在实验过程中，对每个数据集均使用10次10折交叉验证，实验结果保留4位小数，且均使用“均值±标准差”的记录形式。使用WEKA[16]环境下4种常见分类算法以评价各约简算法的分类准确率，其中包括：支持向量机、朴素贝叶斯、决策树以及随机森林。

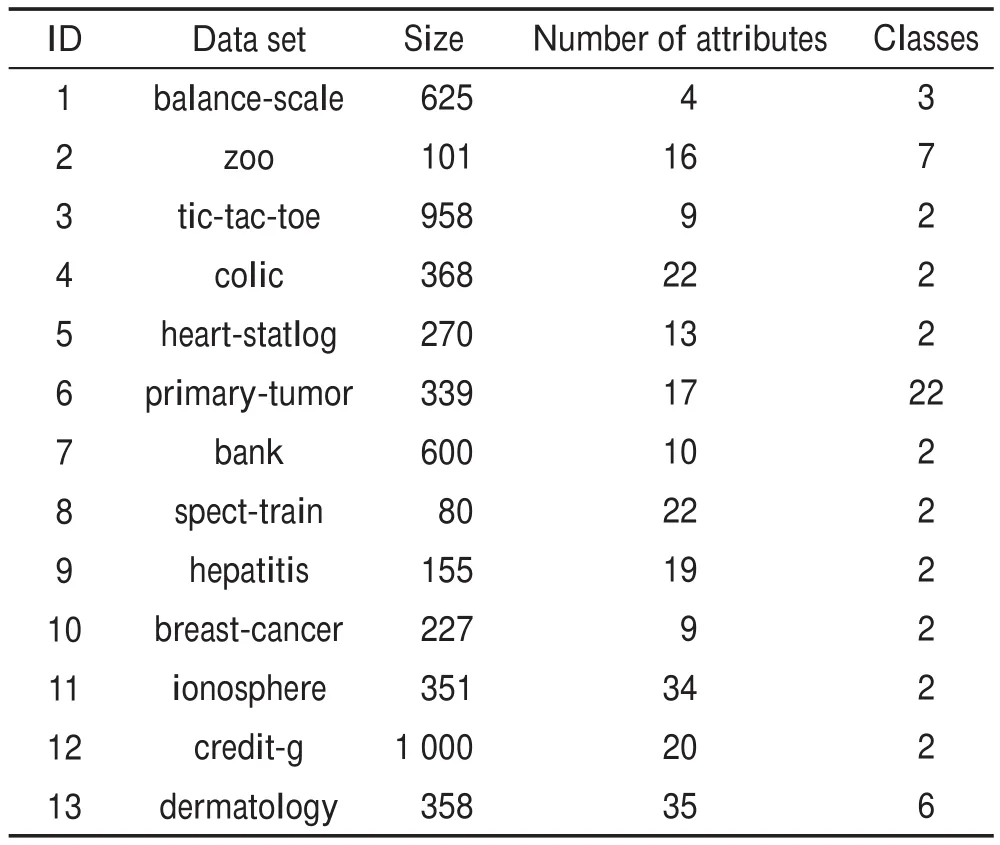
Table 2 Brief description of data sets表2 数据集简要描述

实验结果见表3～表7，在这些表中，PRER（positive region expanded reduction）、MIR（maximum information based reduction）、COR（consistency based reduction）分别表示基于正域扩展、基于最大互信息以及基于一致性的约简方法。同样的，ICSR（inter-classseparability based reduction）代表的是本文基于类间区分度不变准则所提出的属性约简方法。在上述结果比较表中，每行表现最好的约简方法结果均使用加粗处理。进一步的，使用5%显著度的双尾t-检验去检测本文所提出方法的约简结果与其他方法结果之间的差异性。其中使用标志“•”标记劣于本文所提出的方法且与其有显著差异的方法结果值。使用标志“◦”标记优于本文中的方法且与其有显著差异的方法结果值。此外，在以下各表中，对与本文实验结果无显著差异的实验方法结果值均不做任何标记处理。需要补充的是，为更好地对各约简方法的表现性能进行比较，表中使用“Score”行以计数各列所代表方法中出现最好实验结果值的次数。

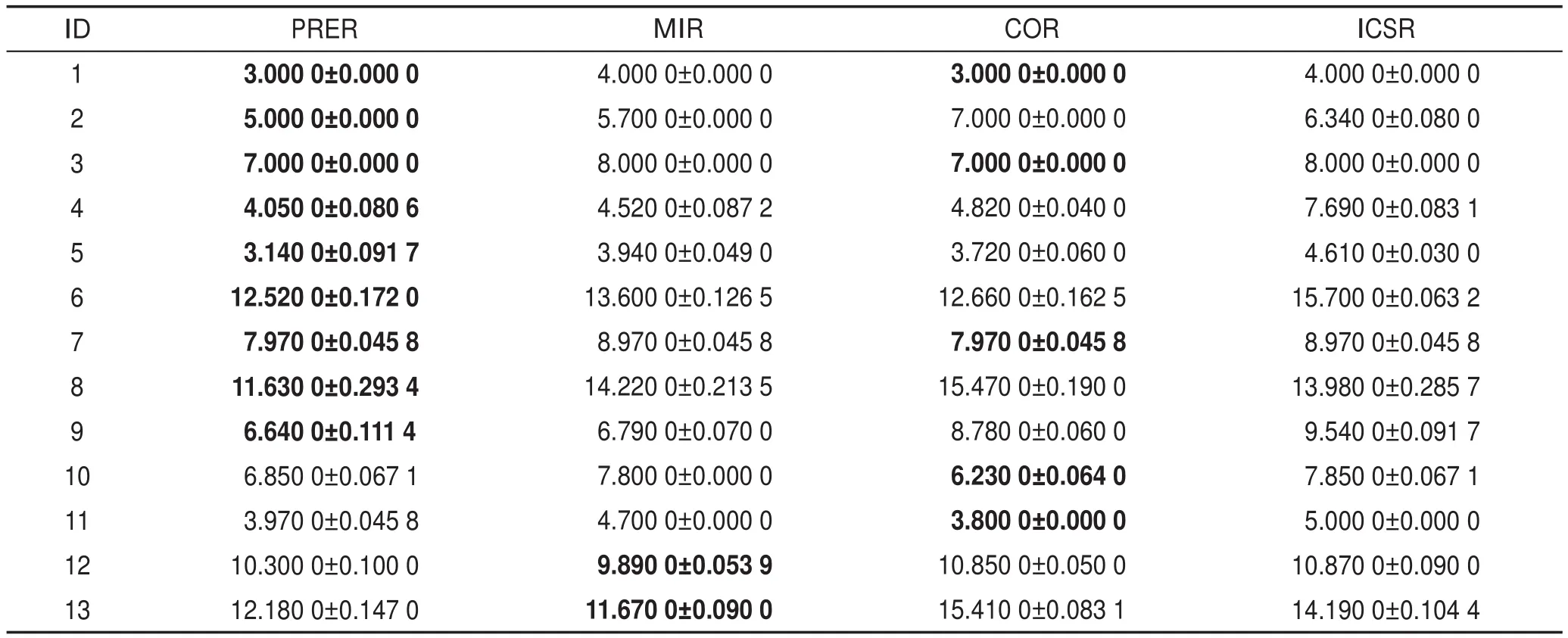
Table 3 Length of reduction of different reduction algorithms表3 不同约简方法约简长度比较

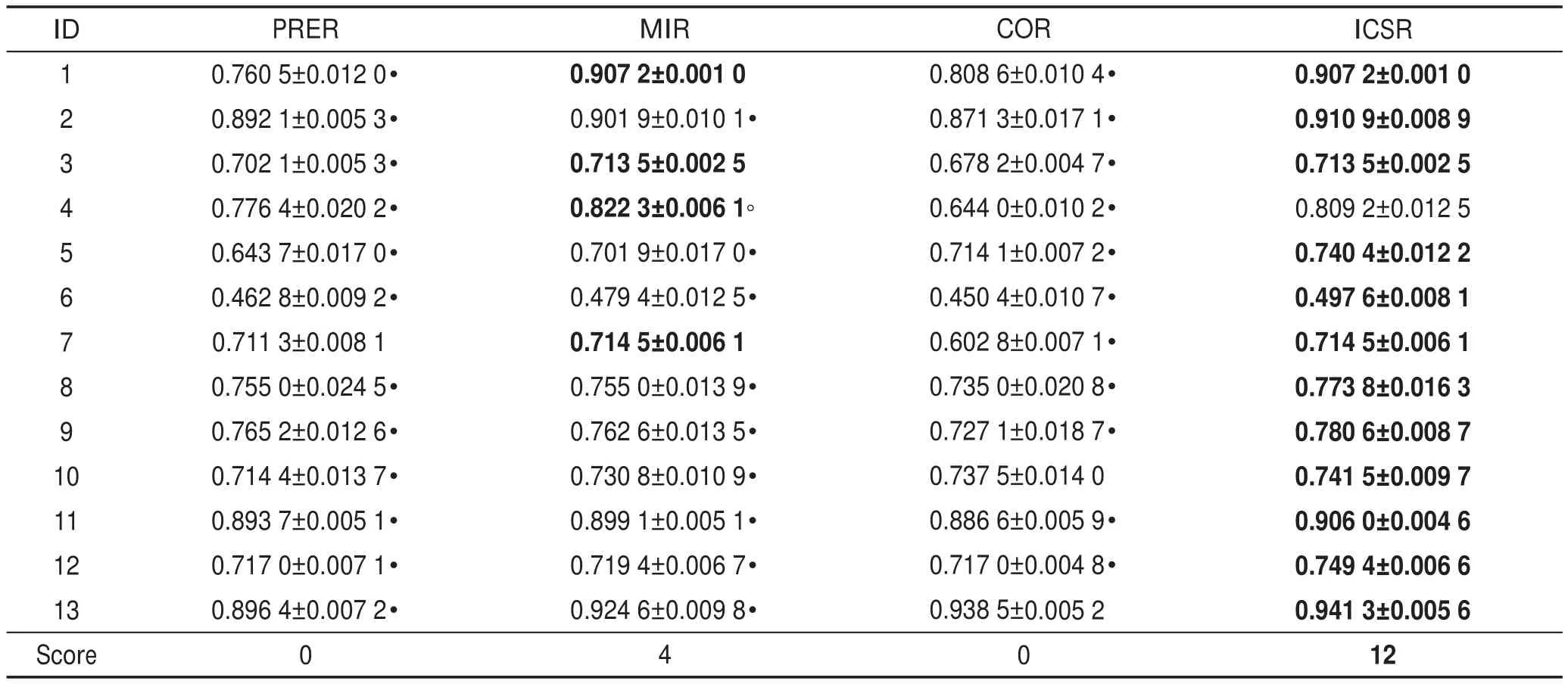
Table 4 Classification accuracy comparison of different reduction algorithms with naive Bayesian表4 朴素贝叶斯分类器下不同约简方法分类精度比较

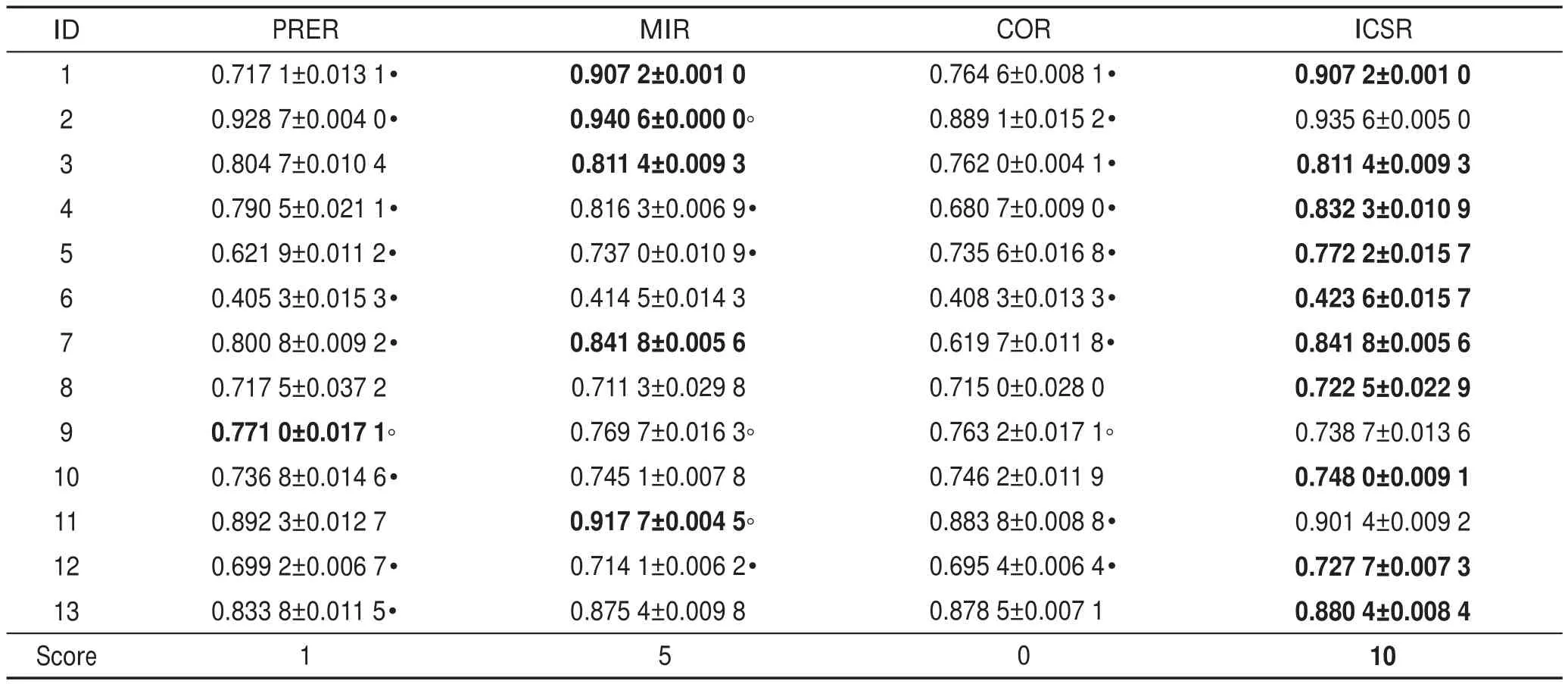
Table 5 Classification accuracy comparison of different reduction algorithms with decision trees表5 决策树分类器下不同约简方法分类精度比较

表3是不同约简方法的约简长度的比较。表4～表7是基于本文所提出的约简方法与其他3种有效的约简方法所求得的约简结果基础上，应用4种不同分类器对各分类精度值的比较。

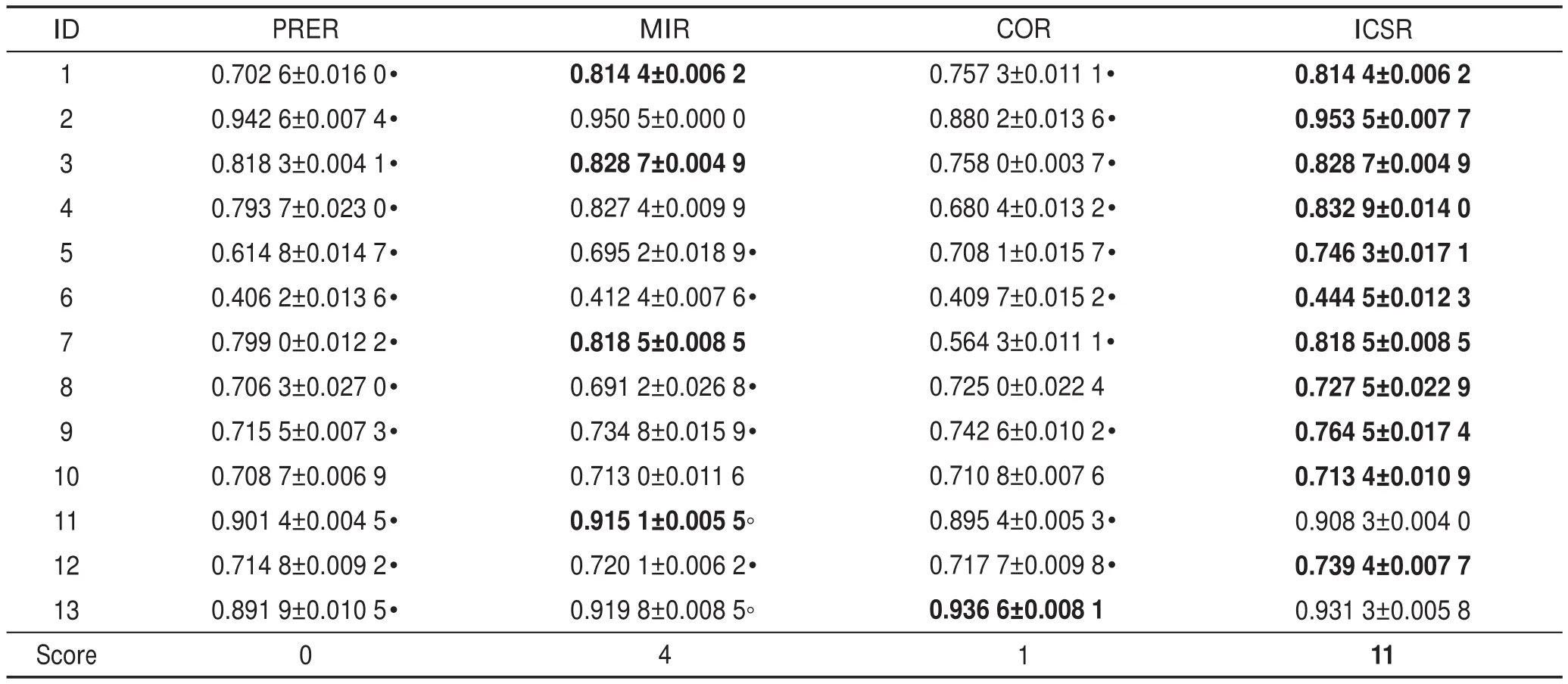
Table 6 Classification accuracy comparison of different reduction algorithms with random forests表6 随机森林分类器下不同约简方法分类精度比较

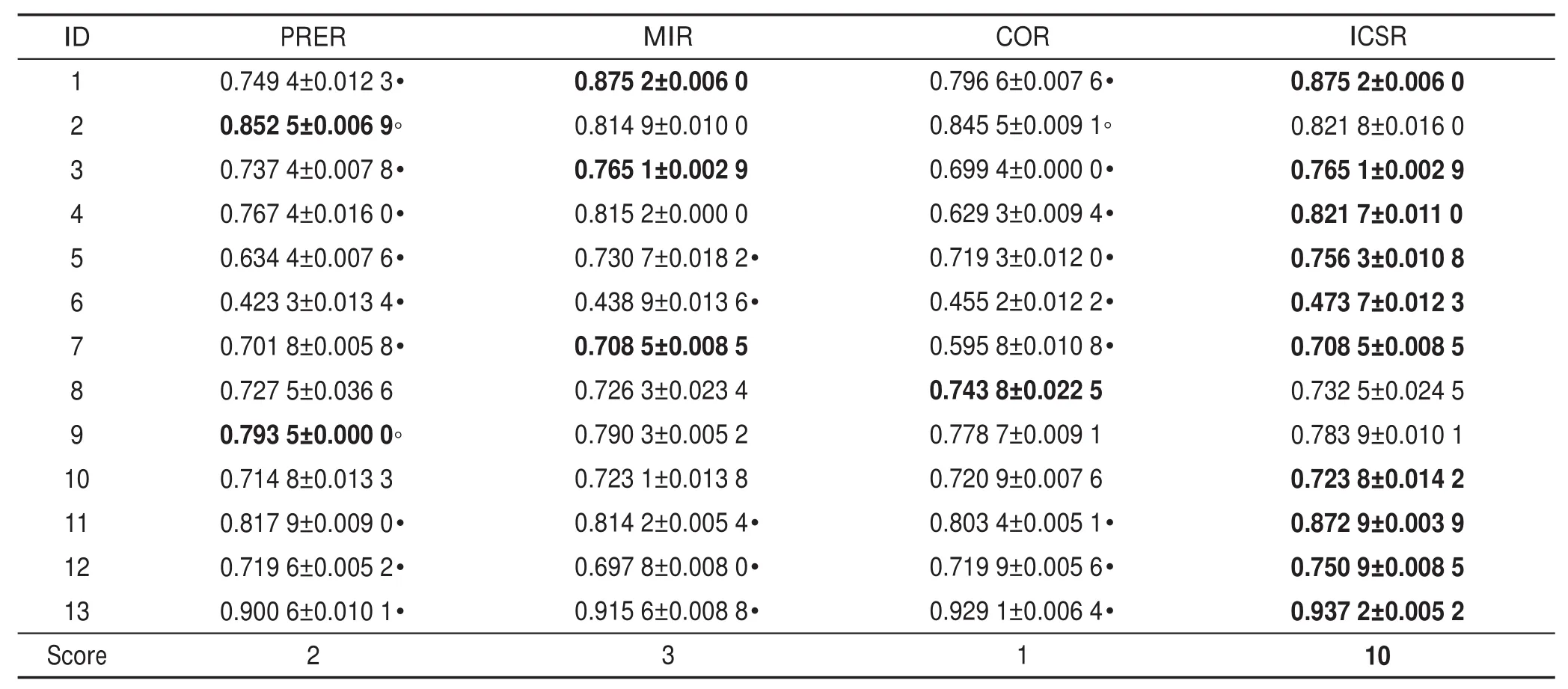
Table 7 Classification accuracy comparison of different reduction algorithms with support vector machine表7 支持向量机分类器下不同约简方法分类精度比较

从表中可以发现：4种约简方法均可在一定程度上有效地减少各数据集的属性数目。在上述各表中，ICSR约简方法在所有分类器上均实现了很好的约简结果，其在大多数数据集上实现了最优分类结果，其中分别包括12、10、11、10次最优分类精度值。相较于ICSR约简方法，PRER约简方法虽实现了最多次最小长度的约简结果，但其仅在4种分类器13个数据集上实现了3次最优分类精度结果。同样的，对于MIR约简方法和COR约简方法而言，二者虽比ICSR约简方法实现了较多次的更短约简长度结果，但其在各分类器上实现最优分类精度结果的次数却远远小于本文所提出的约简方法所实现最优分类结果的次数。

从上述各表实验结果来看，尽管本文所提出的约简方法并未实现最短的约简长度结果值，但其在4个分类器13个数据集的分类精度比较实验中实现最优分类精度值的次数远多于其他3种属性约简方法，且其实验结果值与其他3种方法的实验结果相比具有显著的差异性。此外，上述分类精度及差异性比较实验也表明了本文所提出的约简方法的有效性。

5 结论

属性约简是分类学习中一个重要的问题。针对当前的属性约简方法中较少考虑到各类簇间区分度值的问题，本文将类间区分度的相关概念引入到粗糙集属性约简模型中，提出了一种保持类间区分度不变的属性约简方法。首先，解释并定义了类间重合度，基于重合度概念分析并定义了类间区分度。之后，考虑到类间区分度的相关性质，定义了一种保持类间区分度值不变的属性约简，并基于该约简定义以及启发式搜索策略获得满足相关标准的最小条件属性子集。最后，通过与其他约简方法的对比实验表明本文所提出的方法能够获得具有更高分类准确率的属性约简结果。