关于矩阵Jordan标准形应用及计算

◎任芳国 王甜甜

(陕西师范大学数学与统计学院，陕西 西安 710119)

一、引 言

Jordan矩阵是一种具有良好性质的特殊形状的重要矩阵，通过高等代数的学习，我们知道复数域上任何一个阶方阵都与一个Jordan矩阵相似，且这个Jordan矩阵除去其中Jordan块的排列顺序外由方阵唯一决定.Jordan矩阵是矩阵相似关系中一种形式比较简单的相似标准形，矩阵理论中相当一部分内容都能看作Jordan标准形的应用，因此Jordan矩阵是高等代数教学及矩阵理论的核心内容之一.求矩阵Jordan标准形也是高等代数教学的重点与难点，同时是数学专业硕士研究生入学考试命题的热点问题之一.本文在高等代数教学的基础上，主要讨论Jordan矩阵的性质及应用，并研究了利用矩阵的秩计算矩阵Jordan标准形的理论基础及方法，深化了矩阵Jordan标准形的计算，旨在加深学生对矩阵相似关系及Jordan矩阵的理解和掌握，提高学生学习高等代数的能力并能以Jordan矩阵为工具讨论矩阵中的其他问题.

为了叙述方便，我们对文中符号进行约定：×表示所有×阶复矩阵组成的集合；,()分别表示矩阵的转置和的秩；表示阶单位矩阵；表示第(,)位置元素为1其余位置元素全为0的阶方阵，并约定=0,>或=0,>；∈(=1,…,)表示基本单位向量，即是第个分量为1其余分量为0的维列向量.其他未做说明的符号及概念参见文献.

为了本文讨论更方便需要引入以下定义和引理.

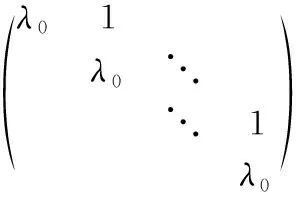
2 设∈×，()=+…++，∈，=0，1,…，，≠0，称矩阵+…++为矩阵关于多项式()的矩阵多项式，记为().

3 设∈×，称关于的多项式det(-)为的特征多项式，记作()；称以为根的次数最低的首项系数为1的多项式称为矩阵的最小多项式，记作().

5 设是阶方阵，是的一个特征值，是一个正整数，约定(-)=，(,)=(-)-1-(-)，称(,)为矩阵关于特征值的Weyr特征.

1 设∈×，任意一个复方阵都与一个Jordan矩阵相似.

2 设∈×，则的最小多项式()等于的第个不变因子().

二、主要定理

先介绍一个Jordan块的性质及其与反序矩阵之间的关系.

1设∈×,()∈[].

(1) 如果=(0)，则()=-，其中1≤≤且=0(≥).

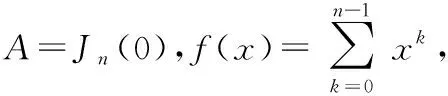
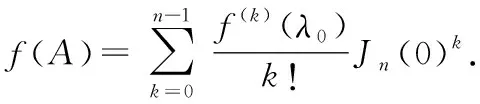
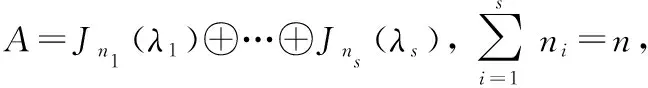
(5)(0)=(0).

(6)(0),(0)都是对称矩阵.

(7)()=().

(8)(),()都是对称矩阵.

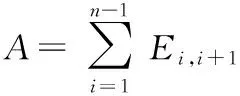
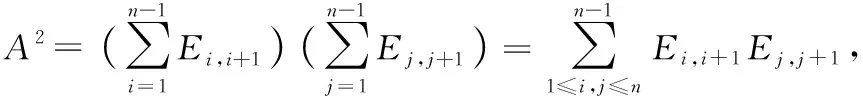
只有当+1=时，,+1,+1=,+1.

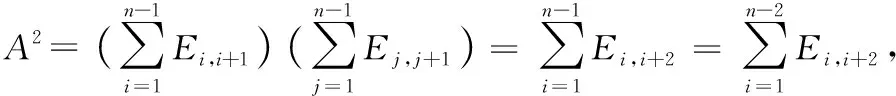
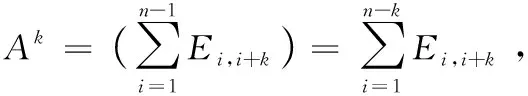
(2)由于-1=(-1)()，由(1)知，=0，则有-=(-)()，所以()=-

(3)将()在处展开，于是由Taylor多项式公式知，

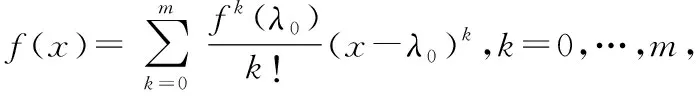
其中=∂(())并约定()=()，

则由(1)知，()-=(0)=0≥，

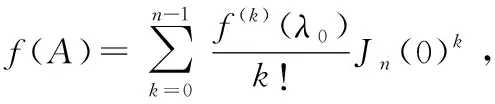
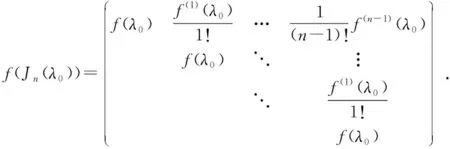
(4)由于Jordan矩阵是分块对角矩阵，则由矩阵多项式的定义及(3)可知(4)成立.

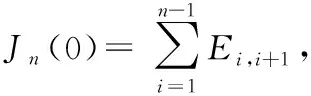
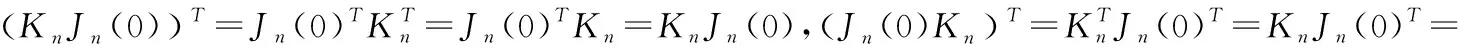
(7)由(5)知，()=(+(0))=()·+(0)=+(0)=().

(8)由于()=(+(0))=+(0)，()=(+(0))=+(0)及(0),(0),都是对称矩阵知，(),()都是对称矩阵.

综上，定理得证.

1设是阶方阵.

(1)方阵与相似.

(2)()=(+1).

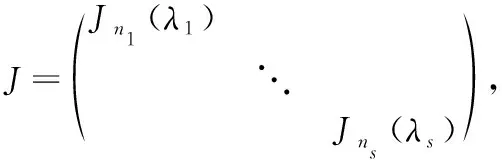
(2) 如果方阵可逆, 显然()=(+1)；如果方阵不可逆，则阶方阵以0为特征值且的Jordan标准形中以0为主对角线元素的Jordan块阶数不会超过，则由定理1(1)知()=(+1).

综上，推论得证.

下面讨论说明任意一个阶方阵都与一个复对称矩阵相似.

2任意一个阶方阵都与一个阶复对称矩阵相似.

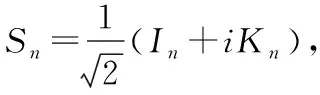
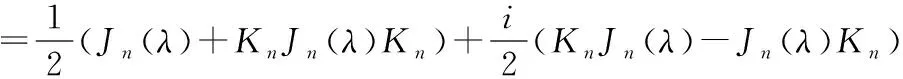
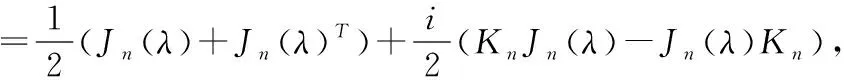
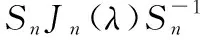
最后由于任意一个阶矩阵都与Jordan矩阵相似，又由上面证明可知，任意一个Jordan块都与一个对称矩阵相似，从而任意一个阶矩阵都与复对称矩阵的直和相似，故任意一个阶矩阵都与一个复对称矩阵相似.

综上，定理得证.

在线性代数课程中已经学习过利用初等变换求矩阵的Jordan分解，现在讨论利用矩阵的秩计算矩阵的Jordan标准形.

3设是阶方阵，是的一个特征值且作为最小多项式()根的重数为

(1)在的Jordan标准形中特征值对应的最大Jordan块的阶数等于

(2)特征值在的Jordan标准形中对应的Jordan块的个数等于的几何重数，即(,)=-(-).

(3)(-)=(-)(≥).

(4)dim{|(-)=0}等于特征值的代数重数.

(5)(,)等于的Jordan标准形中特征值为且阶数至少为的Jordan块的个数.

(6)(,)-+1(,)等于的以特征值为主对角线元素且阶数为的Jordan的个数，其中∀∈.

(7)(,)是的以特征值为主对角线元素且阶数为的Jordan块的个数，且当>时，(,)=0.

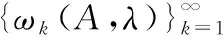
(1) 由于矩阵的最小多项式()是矩阵的第个不变因子，即矩阵的所有不同特征值对应的同一个一次因式方幂中次数最高的初等因子的乘积，而矩阵的初等因子与矩阵的Jordan标准形中的Jordan块有一一对应关系，那么初等因子的次数就是Jordan标准形中对应块的阶数，所以特征值对应的最大Jordan块的阶数等于作为最小多项式()根的重数.

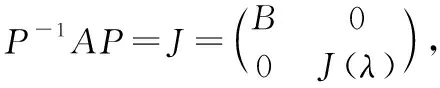
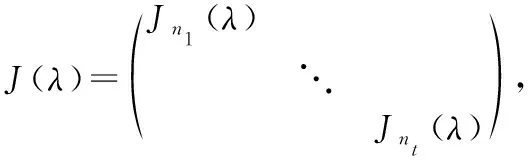
即是(-)阶方阵，特征值的代数重数为，以特征值为主对角线元素的Jordan块有个.

(2) 由与相似知，-与-相似，那么

(-)=(-)

=(()-)+(--)

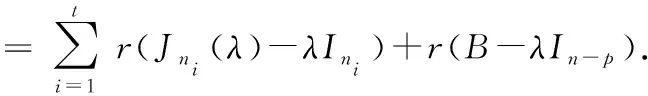
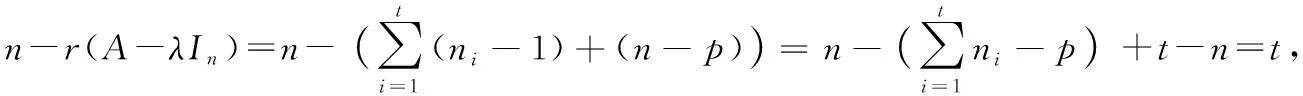
(3)由于-=(()-)⊕…⊕(()-)⊕(-)=(0)⊕…⊕(0)⊕(--).

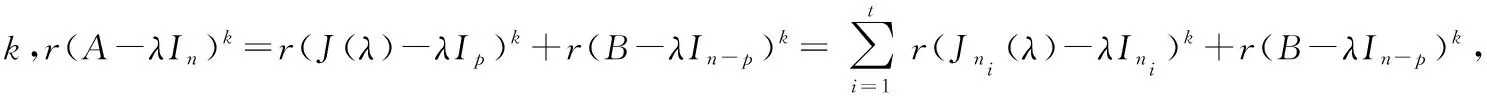
(4)由于dim{|(-)=0}=-(-)，再由(3)知(-)=(--)=-，

故dim{|(-)=0}=-(-)=，即为特征值的代数重数

(5) 由于

-=(()-)⊕…⊕(()-)⊕(-)=(0)⊕…⊕(0)⊕(--),

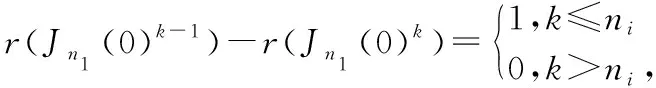
(6) 由(5)可知(6)成立.

(7) 由(1)可知的Jordan标准形以特征值为主对角线元素的最大Jordan块的阶数为，则当>时，(-)=(-)-1，所以(,)=0，再由(5)可知(,)是以特征值为主对角线元素且阶数为的Jordan块的个数.

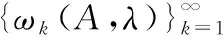
综上，定理得证.

现在根据定理3可得到利用矩阵的秩计算矩阵Jordan标准形的步骤.

2设为阶方阵，利用矩阵的秩计算的Jordan标准形四个步骤：

(1)利用特征多项式()，求阶方阵的所有不同的特征值,=1,…,

(2)对每个相异的特征值,=1,…,，及每个=1,…,，分别求出(,).

在计算中首次出现，使得(,)=+1(,)终止计算，即为在Jordan标准形中对应的最大Jordan块的阶数. 当某个特征值的代数重数为1时，它在Jordan标准形中所对应的Jordan块只有一个一阶Jordan块，不需要计算(,).

(3)对每个特征值分别求出对应的各级Jordan的阶数与个数.

()=(,)-(,)=-2(,)+(,),

()=(,)-+1(,)=-1(,)-2(,)++1(,),=1,…,,

其中()为Jordan标准形中以特征值为主对角线元素的阶Jordan块()的个数.

(4)写出方阵的Jordan标准形.

方阵的Jordan标准形由的每个特征值所对应的()个以为主对角线元素的阶Jordan块按照某一确定的次序产生的直和所构成.

三、结束语

Jordan矩阵是一种具有良好性质的形状特殊的重要矩阵，本文利用矩阵运算、反序矩阵、矩阵相似关系及矩阵的秩，深化了Jordan矩阵的性质，并在此基础上给出了任意阶方阵与对称矩阵相似的构造性证明及利用矩阵的秩计算矩阵Jordan标准形的理论基础，最后总结了利用矩阵秩计算矩阵Jordan标准形的步骤，并通过例题加深了Jordan标准形的计算，促进学生提高学习高等代数的能力，以上研究进一步说明了Jordan矩阵在高等代数教学及矩阵理论中的重要性.