规则波浪对水下航行体出水姿态参数的影响

职明洋， 马贵辉， 任泽宇, 赵建洲

(哈尔滨工程大学船舶工程学院， 哈尔滨 150000)

0 引言

水下航行体出水是一个复杂的流固耦合过程，航行体出水时主要经历水下航行阶段和出水阶段。在出水阶段，航行体的运动受到波浪的扰动，波浪和航行体的相互作用影响了其出水姿态，以至于影响出水后的二次调整甚至会导致发射失败，所以研究波浪对航行体出水姿态参数的影响过程及规律对丰富航行体的波浪条件下出水过程有着重要意义。

波浪对水下航行体的扰动属于流固耦合问题，求解流固耦合问题的数学模型主要包括Navier-Stokes(N-S)模型和理想势流模型。对于N-S模型的求解，基本思路是针对N-S方程和连续性方程所组成的控制方程组，选择不同的离散方法和流动模型，其中在出水方面应用较为成功的算法包括流体体积法(VOF)、水平集和流体体积耦合法(CLSVOF)、标记网格法(MAC)、浸没边界与流体体积耦合法(IBM-VOF)及光顺粒子法(SPH)等。虽然N-S模型可以考虑流体黏性的影响，但其对于计算资源需求大，在工程预报方面，计算效率相对较低。经典的势流模型在数学上做了简化处理，大部分计算认为流体是无黏不可压缩的，Sun等采用基于势流理论模型的边界元方法，应用非线性自由表面条件，对船舶在规则波中的响应进行了3D时域分析，当波浪高于船舶甲板高度时，波面最高点和船首甲板高度差的变化周期与入射波的周期相同，的峰值与波高呈正相关；Yu等通过势流理论和面板单元法，针对张力腿式平台进行了一系列的系泊分析，以预防平台在极端海况下失效。Ma等基于势流理论，建立了完全非线性的数值水池，计算了波浪与垂直圆柱之间的相互作用，通过验证发现在波浪不发生破碎的情况下，考虑流场黏性与不考虑流场黏性时两者计算结果差距很小。Ni等采用理想势流模型对航行体壁面的气泡行为进行了研究，进一步验证了理想势流模型在求解流固耦合问题上的有效性。对于波浪与结构物的耦合作用，大量研究主要针对舰船、水下潜器、海洋平台等方面，关于波浪扰动在水下航行体出水问题中的影响研究较少。

出水问题是指水下航行体穿过空气-水界面并释放到空气中的过程，涉及非线性变形的复杂问题。Takamure等通过实验研究了小球出水时自由液面的变形情况以及能量转化问题，发现当发射深度和小球半径之比高于一定的临界值时，动能会以固定比例转换为势能，而且此时被小球穿过的自由液面的变形自相似。Wu等设置了多功能出水实验装置用于研究小球自由出水和强迫出水问题，结果表明，小球强迫出水后，自由面所形成的水柱高度会随着傅汝德数的增加而增加，但是，水柱的持续时间会减少，小球自由出水时，受到的流体力主要来自加速度。所以，通过实验研究发现，结构物穿越自由液面的过程中，涉及自由面变形和水层破裂等难题，学者们一直致力于该问题的解决。Liju等采用约束式运动平台，研究不同尺度模型在不同运动速度下出水时自由液面的变化，同时通过边界元方法模拟该出水过程，与实验对比良好，但其关注的重点在于物体穿越自由液面之前，未计算自由液面的破裂。Rajavaheinthan等采用时间差分迭代求解圆柱出水过程，但是计算结果被迫在自由面破裂之前终止。直到倪宝玉提出一种水层脱落法，当自由面与结构物之间的水层厚度小于某一临界值时，认为自由面断裂，结构物出水。目前，结构物出水时自由液面大变形问题的处理方法局限于结构物固定不动或者是运动轨迹已经确定的情况，但是在实际的水下发射过程中，航行体出水姿态倾斜，对于该方面的出水研究较少。

Wang等基于动态网格技术建立了水下航行体三维出水弹道模型，该模型的建立为出水轨迹的研究提供了参考。朱坤等采用Mixture模型研究了波浪相位对水下航行体出水过程中水动力学特性的影响，发现波浪相位会导致航行体肩部空泡空间几何的不对称，进而引起航行体表面水动力分布的不对称性。权晓波等将二阶Stokes波的波面运动速度耦合到入射边界条件中，采用有限体积法研究了五级海况下水下航行体出水时的位置偏移，研究发现相对于静水出水，五级海况下水下航行体完全出水后弹体尾部偏移1 m。陈超倩等基于独立膨胀原理对水下航行体的水下弹道进行了仿真，所得结果和实验数据对比良好，验证了计算的有效性，发现发射潜艇的速度使弹道轨迹出现弯曲，航行体俯仰角偏差持续变大，不利于航行体姿态的稳定，且艇速越大，出水姿态角越大，在计算过程中虽然考虑了空化，但是空化模型对水下弹道的影响不大。张重先运用Morison公式，对波浪影响下水下航行体的出水过程进行了仿真，波浪相位对波浪扰动的大小和方向均有影响，且影响效果最为显著，水下航行体的小尺寸性和快速性有利于降低波浪对水下航行体的扰动作用。虽然前人对波浪影响下水下航行体的出水姿态做了一定的研究，但是波浪参数对水下航行体出水姿态的影响缺少系统、全面的论述。

本文基于边界元方法，采用规则波浪模型计及波浪入射势，建立了波浪作用下的航行体出水模型，采用截平面的方法将航行体出水模型做了简化处理，并与实验数据进行了对比，验证了模型的有效性。模拟了航行体在不同波浪条件下的出水姿态，研究了浪向、波高、初相位以及周期对水下航行体的出水姿态的影响，对水下航行体出水姿态参数进行了时域分析。

1 理论与方法

本章应用势流理论建立水下航行体出水的数值模型，内容包括：1)基本的控制方程及边界条件；2)波浪模型及入射势；3)网格划分及单元映射过程；4)航行体出水过程模型简化；5)有效性验证。图1为本文物理模型的示意图。

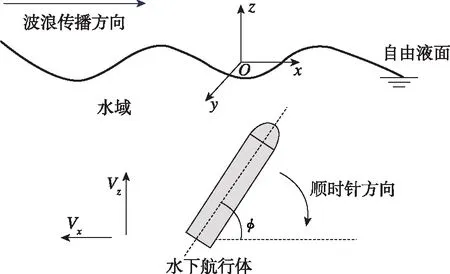
图1 物理模型示意图Fig.1 Schematic diagram of physical model

航行体的出水过程是一个复杂的非线性流固耦合过程，本文基于边界元方法建立了波浪作用下的航行体出水模型，具体计算流程如下：

1)在初始条件下将航行体表面单元、节点的相关信息输入到三维计算程序中，计算得到速度势；

2)将速度势输入到式(8)中，可以得到航行体表面压力；

3)通过航行体运动学方程计算受力后航行体整体的运动响应；

4)得到更新后的时间步时刻的航行体表面单元、节点的相关信息；

5)重复迭代计算以上步骤，直到航行体出水过程结束。

1.1 控制方程及边界条件

假定流体为理想流体，无旋，不考虑黏性作用，计算过程中考虑波浪的影响，将总速度势由波浪入射势和结构表面扰动势组成，即

=+

(1)

满足拉普拉斯方程

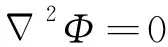
(2)

根据势流基本理论，方程满足以下边界条件:

结构表面满足不可穿透条件

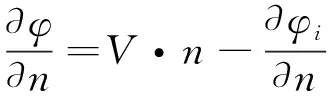
(3)

式中，为航行体表面法向，为边界运动速度矢量。

流场无穷远处满足边界条件

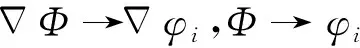
(4)

即认为航行体扰动势在无穷远处对流场无影响。

自由液面(在=(,,)处)边界条件

dd=0

(5)

代入伯努利方程并且摄动展开后保留一阶项得到

(6)

式(6)满足平面进行波的运动方程，是线性化的自由液面条件。

对于扰动势，根据格林公式可以用其边界上的速度势及其法向导数来确定，所以需要采用边界积分方法求解流场扰动势

()=

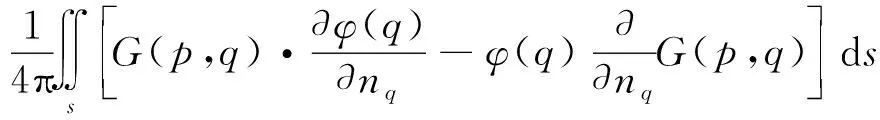
(7)

式中，为航行体表面边界面，和分别为场点和源点。自由空间的格林函数为(,)=1|-|，和分别为场点和源点的位置矢量。

将求解得出的速度势带入非定常的伯努利方程中，对水下航行体在运动过程中所受的压力进行求解，求解过程中需要计算流场静压和大气压力，求解公式如式(8)所示

(8)

式中,为大气压。

式(8)即航行体受力迭代式，可以认为其和边界条件(3)构成了本文数值方法的基础。

1.2 波浪模型及入射势

考虑到本文所有工况计算中波高相对于水深为小量，因此选取的波浪模型为满足重力波周期性解的规则微幅波模型，进而采用微幅波理论对水下航行体在规则波浪中的运动进行分析。微幅波模型如图2所示，图中，为波长，为波高，为波幅。

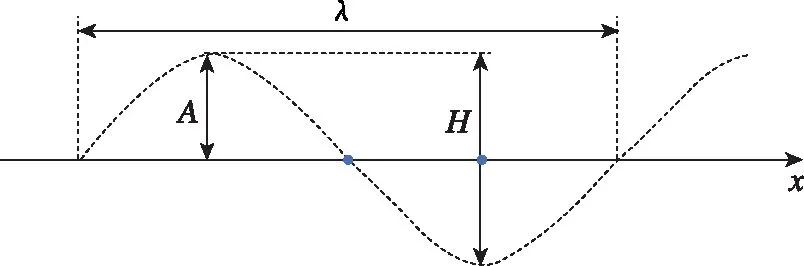
图2 微幅波波面Fig.2 Small amplitude wave surface

微幅波面方程如式(9)所示。

(,)=cos(-+)

(9)

式中，代表波浪频率，代表波数，代表初相位，即初始时刻相位。

微幅波理论中，水质点运动缓慢，同时注意到微幅波中势函数位移偏导较时间偏导为小量，故自由表面非线性边界条件可以简化为线性边界条件，将微幅波问题简化为线性问题。因此，波浪向前传播时，波浪的入射势为

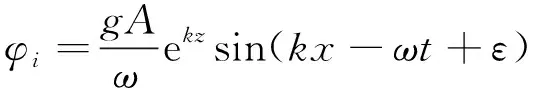
(10)

假定波浪传播方向与固定坐标系存在夹角，则微幅波经过坐标转换，可得到新的数学模型

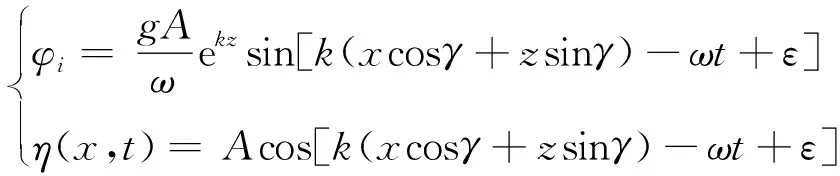
(11)

在本文中航行体水平速度方向和波浪传播方向相同时为顺浪，此时=180°；相反时为逆浪，此时=0°；两个方向相互垂直时为横浪，此时=90°，范围为0°～180°。

根据入射势，流体质点运动速度为

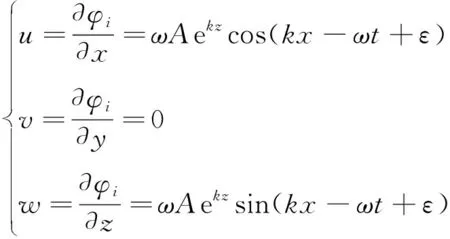
(12)

1.3 网格划分及单元映射过程

首先对航行体结构表面离散化处理，离散过程如图3(a)所示，由于结构表面三角形单元形态各异，需要把所有单元映射到平面上的直角三角形内，以便将各单元以同一标准参数化。

(a)结构表面离散

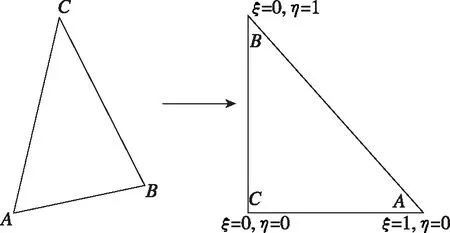
(b)单元映射过程图3 网格处理Fig.3 Grid processing

映射如图3(b)所示，分别把和映射到坐标轴和上，三角形的3个顶点分别落在(1，0)，(0，1)和(0，0)上，线性插值分别用于表示几何位置函数，速度势函数以及速度的法向分量=∂∂，三角形的3个顶点分别用1,2,3来表示，则插值公式如下所示

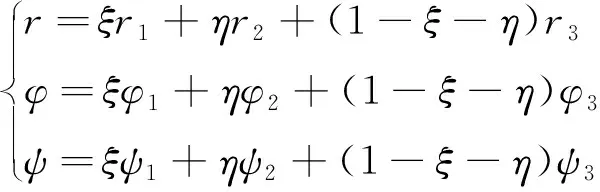
(13)

三角形在公式(7)的第一项积分为

=++

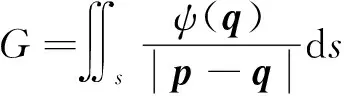
(14)

式中，是三角形从整体坐标系到局部坐标系(,)上的雅克比转换。

另外，积分公式右端在所选单元上的积分可表示为

=′+′+′

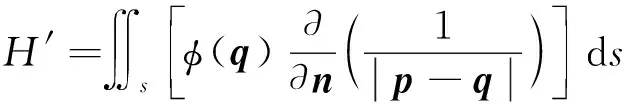
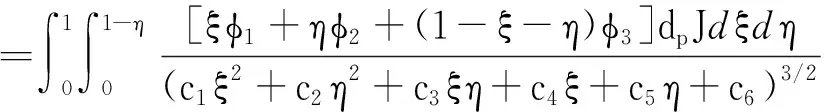
(15)

式中,=·(-)，为三角形单元的法向量。

令=′+，其中,=1,2,…，，可将积分方程(7)简化为矩阵形式

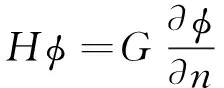
(16)

1.4 水下航行体出水过程模型简化

本文对于航行体穿越自由液面时涉及的相变以及网格重塑问题进行了简化处理，如图4所示，对于节点的重塑，超过自由液面的节点将会被祛除，并且在截取出来的面上设置一个节点作为中心点，节点信息的确定采用以下思路：对于单元的祛除，三角形单元的3个节点只要有1个节点超过自由液面那么该单元就会被删除，但是有一种情况特殊，当三角形单元的3个节点有2个节点在自由液面以下，另外1个节点称之为特殊节点()(=0,1,2…,,为所有该类型节点的总数)在自由液面以上时，node()的节点信息将会被用于节点信息的更新，即通过截面上方所有特殊节点()的运动参数表示截面新节点的运动信息

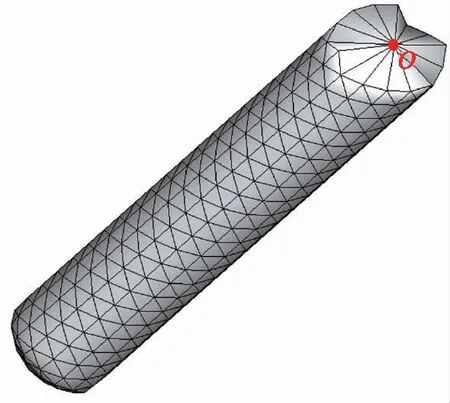
图4 平面截取后的水下航行体Fig.4 Underwater vehicle after plane interception

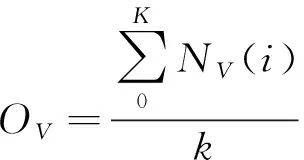
(17)

式中，和分别为点和特殊点的坐标，和分别为点和特殊点的节点速度，自由液面以下的航行体部分继续计算，直到航行体尾部出水。

1.5 有效性验证

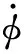
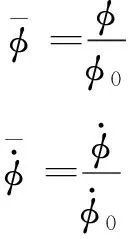
(18)

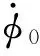
为验证算法的有效性，将在开放水池测得的试验结果与数值模拟结果对比。试验为本文工况之一：航行体初始水平速度为，垂直速度1666，波面状态为静水。对比结果如图5所示。

(a) 无量纲俯仰角数值模拟和实验对比

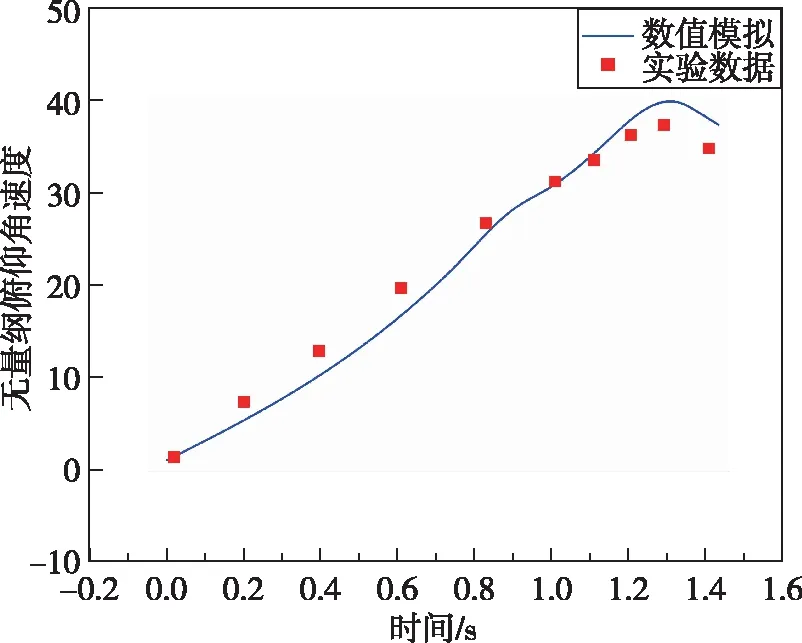
(b) 无量纲俯仰角速度数值模拟和实验对比图5 水下航行体数值模拟和实验的俯仰姿态对比Fig.5 Comparison of pitching attitude between numerical simulation and experiment

通过对比发现数值模拟和实验的俯仰姿态结果对比良好，但是在航行体出水阶段，由于对航行体出水条件的简化，采用了以截平面节点代替出水航行体的方法，忽略了航行体在空气中的运动和结构变化，导致该阶段的偏差较水下运动阶段的误差大，航行体尾部触水时俯仰姿态相对误差如表1所示，实际误差较小，可以认为计算方法有效。

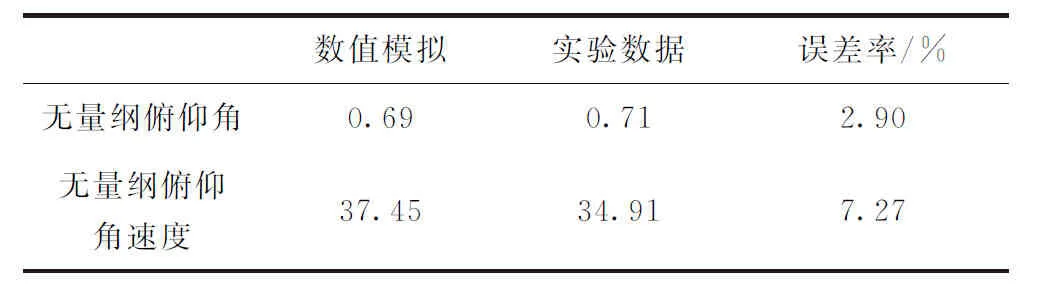
表1 航行体尾部触水时数值模拟和实验数据的俯仰姿态参数对比Tab.1 Comparison of pitching attitude between numerical simulation and experiment when the tail of an underwater vehicle touches the water

2 结果与讨论

2.1 静水条件下出水姿态参数分析

在分析波浪参数对水下航行体出水姿态参数影响之前，需要对本文研究的出水姿态参数变化有一个较为完整的认识，因此忽略波浪的作用，分析水下航行体在静水条件下姿态参数变化。静水条件下水下航行体的无量纲俯仰角和无量纲俯仰角速度变化曲线如图6所示。

图6 静水条件下无量纲俯仰角和无量纲俯仰角速度变化Fig.6 Comparison of dimensionless pitch angle and dimensionless pitch angular velocity under static water conditions

头部触水(HT)之前为水下运动阶段，运动中的航行体受到的力主要是竖直方向的重力与浮力以及水平方向的流体作用力，由于其流体作用力的等效作用点位于质心前方，在转矩的作用下导致航行体做顺时针旋转运动。航行体上升阶段做俯仰运动，其受力不平衡性进一步加剧，从而导致航行体的无量纲俯仰角速度不断地增大以及无量纲俯仰角不断地减小。头部触水和尾部触水(TT)之间为出水阶段，航行体湿表面积不断减小，整体所受浮力不断下降，流体作用力的作用点不断下移并逐渐位于质心下方，同时航行体受到的流体作用力也在不断减小，其产生的作用可以使得航行体有逆时针转动的趋势，所以可以看到航行体无量纲俯仰角速度在尾部触水之前不断减小。

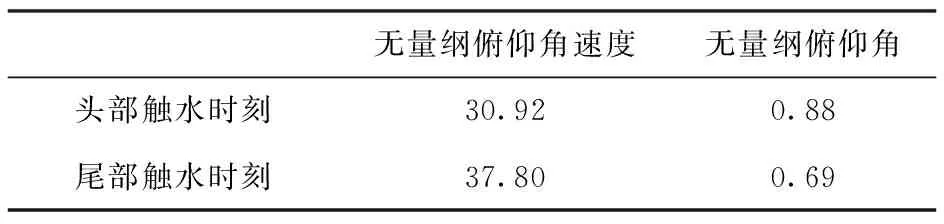
表2 静水条件下头部接触水时刻和尾部接触水时刻的无量纲俯仰角和无量纲俯仰角速度Tab.2 Dimensionless pitch angle and dimensionless pitch angular velocity at the moment when the head touches the water surface and the moment when the tail touches the water surface under static water conditions

2.2 波高对出水姿态参数的影响

(a) 无量纲俯仰角曲线

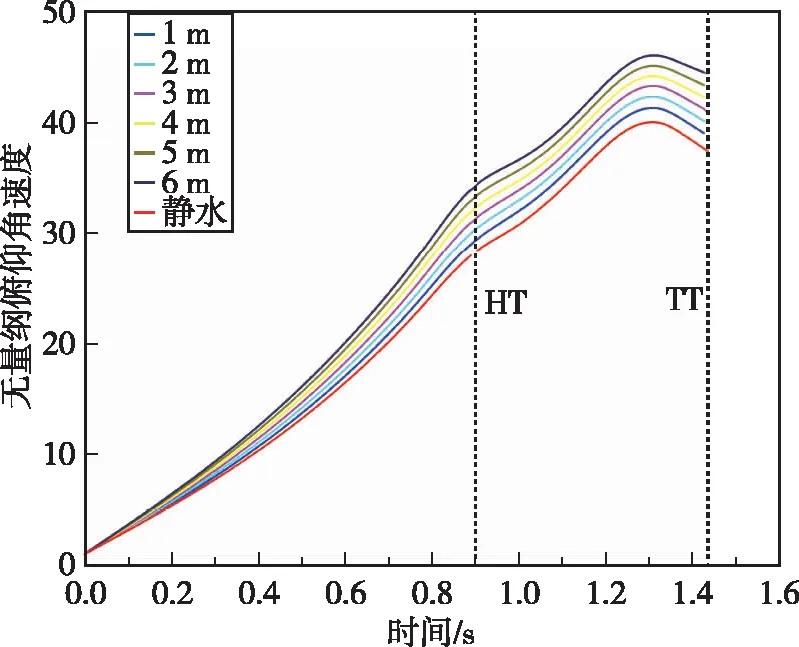
(b) 无量纲俯仰角速度曲线图7 逆浪条件下波高对出水姿态参数的影响Fig.7 Influence of wave height on water-exiting attitude parameters under the condition of head seas

在水下航行体实际发射过程中，往往会更加注重头部触水时刻和尾部触水时刻的出水姿态参数，为了更好探究两个时刻的出水姿态参数同静水条件下的出水姿态参数的关系，将逆浪条件下，头部和尾部触水的无量纲俯仰角和无量纲俯仰角速度与静水条件下的做比较，得到俯仰角偏差值和俯仰角速度偏差值

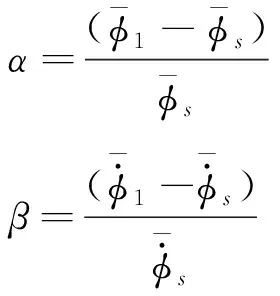
(19)

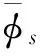
得到的不同波高影响下的出水姿态参数偏差如图8所示，可以发现俯仰角偏差呈负数，俯仰角速度偏差呈正数。根据式(19)可以发现，在逆浪条件下，相比于静水，波高会增加航行体的俯仰程度，不利于发射成功，对水下发射呈负影响；随着波高的增加，俯仰角和俯仰角速度偏差值近似呈线性增加，说明随着波高的增加，波浪力也逐渐增加并对航行体尾部触水无量纲俯仰角的影响越来越大。

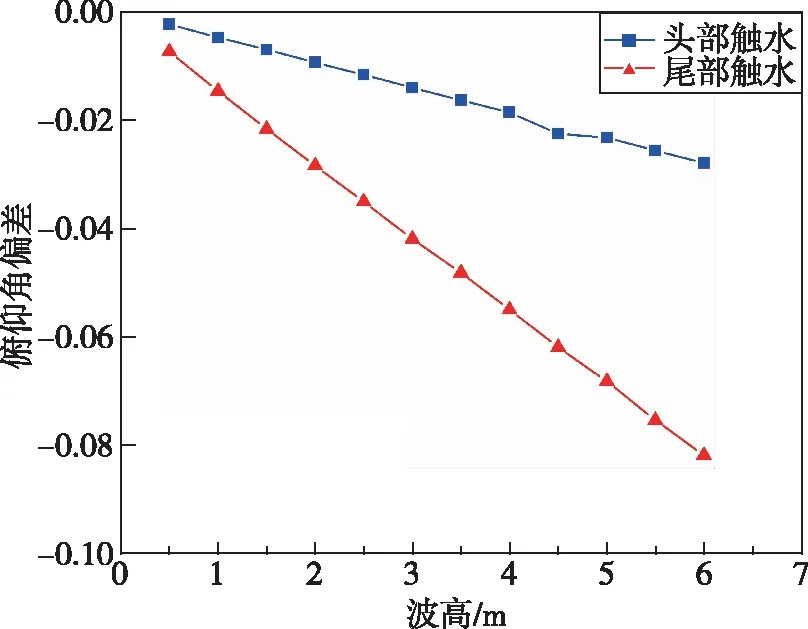
(a) 俯仰角偏差

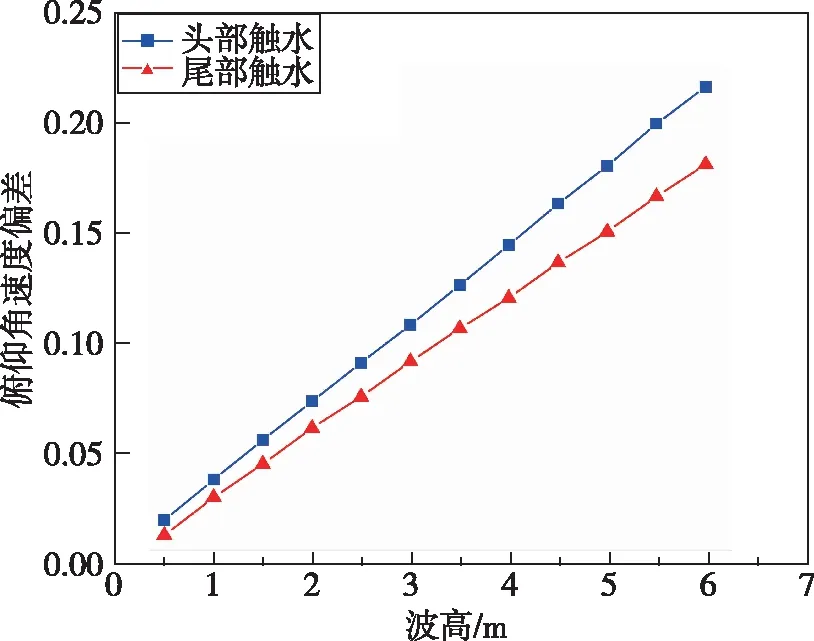
(b) 俯仰角速度偏差图8 逆浪条件下波高对俯仰角和俯仰角速度偏差值的影响Fig.8 Influence of wave height on pitch angle and pitch angular velocity deviation under the condition of head seas

如图9所示，顺浪条件下波高对出水姿态参数的作用规律和逆浪条件下的相反，虽然出水姿态参数的变化规律仍然不变，但是该工况下的无量纲俯仰角大于静水的无量纲俯仰角，无量纲俯仰角速度小于静水的无量纲俯仰角速度。即相比于静水，波高能够抑制航行体的俯仰变化，对水下发射呈正影响，而且随着波高的增加，对航行体俯仰变化的抑制效果更加显著。

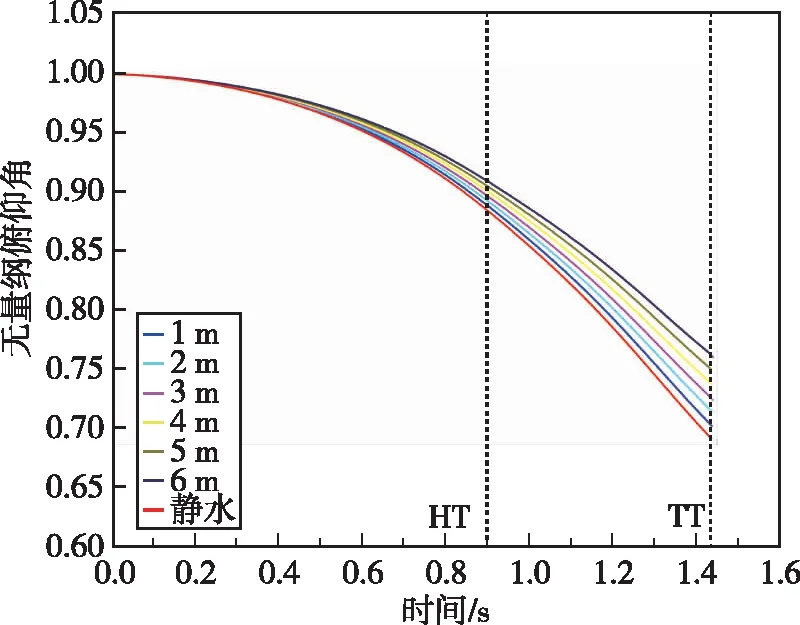
(a) 无量纲俯仰角曲线

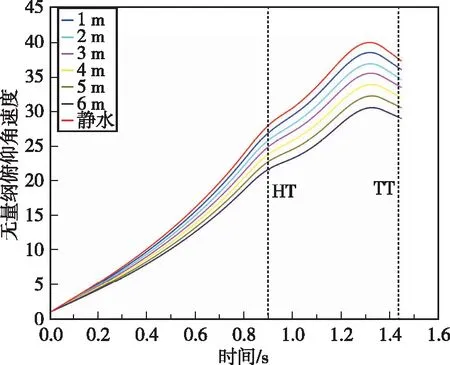
(b) 无量纲俯仰角速度曲线图9 顺浪条件下波高对出水姿态参数的影响Fig.9 Influence of wave height on water-exiting attitude parameters under the condition of following seas

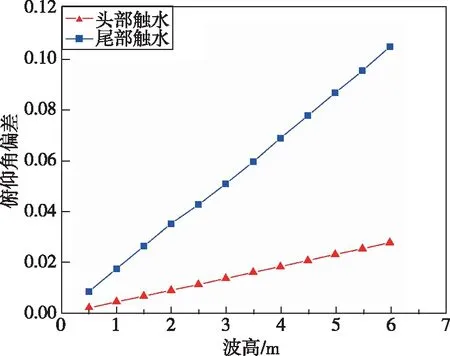
将顺浪条件下，头部和尾部触水的无量纲俯仰角和无量纲俯仰角速度与静水条件下的做比较，如图10所示,俯仰角偏差>0，俯仰角速度偏差<0，顺浪条件下不同波高对航行体的俯仰程度呈正影响，俯仰角和俯仰角速度偏差仍然呈线性变化。

(a) 俯仰角偏差

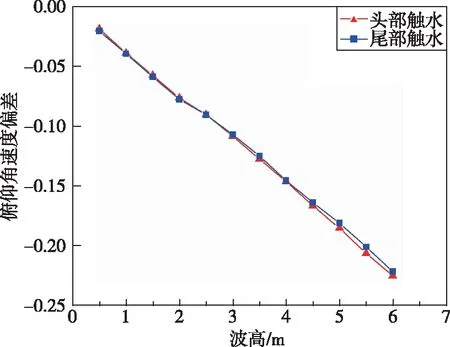
(b) 俯仰角速度偏差图10 逆浪条件下波高对俯仰角和俯仰角速度偏差值的影响Fig.10 Influence of wave height on pitch angle and pitch angular velocity deviation under the condition of head seas

2.3 周期对出水姿态参数的影响

周期为两个相邻波峰经过海面上同一点的时间间隔，周期越长的波浪完成该过程所需的时间就越长，由于频率=2π，且由式(10)可得出水相位

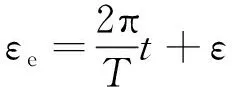
(20)

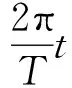
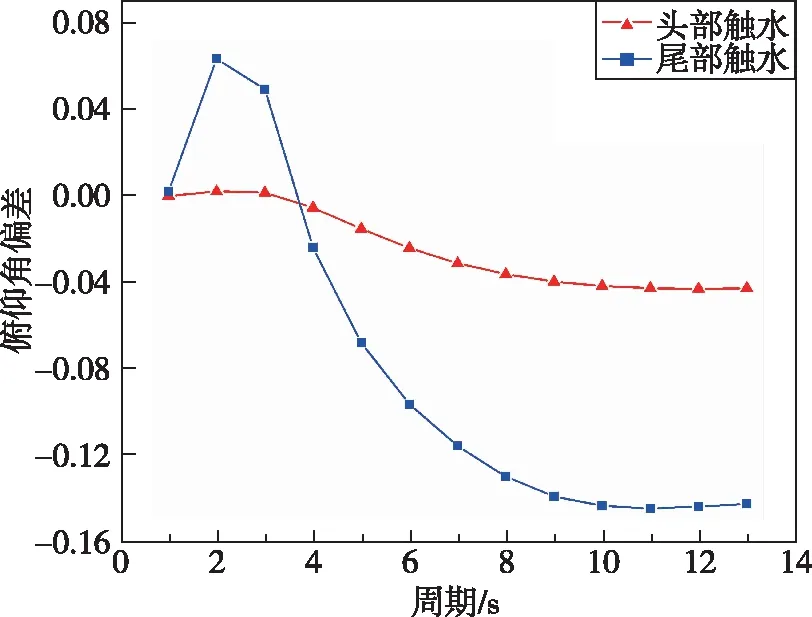
在本节计算中，浪向为逆浪，波高取1.88 m，初相位0°，周期取1～13 s，间隔1 s，得到头部和尾部触水的无量纲俯仰角和无量纲俯仰角速度与静水条件下的偏差，所得结果如图11所示。相同浪向、波高和初相位的情况下，周期较小时，由式(20)可知，相位改变量较大，出水相位由相位改变量和初相位共同决定，所以图11中俯仰角偏差和俯仰角速度偏差在小周期阶段有较大起伏；而周期较大时(≥10 s)，频率对时间的敏感度降低，加之水下航行体在水中停留时间极短，相位改变量较小，出水相位和初相位近似相等，各周期工况下航行体出水相位大致接近，此时周期对出水相位的影响较小，所以图11中俯仰角偏差和俯仰角速度偏差在大周期阶段的曲线近乎水平。

(a) 俯仰角偏差

(b) 俯仰角速度偏差图11 周期对出水姿态偏差的影响Fig.11 Influence of period on water-exiting attitude deviation

因此，周期通过影响航行体水下航行阶段这一过程中波浪的相位变化，进而间接影响了航行体出水时刻的相位。周期的变化对相位的影响呈负相关，周期较小工况对航行体出水姿态影响大于周期较大工况对其姿态的影响。同时注意到实际工程中波浪周期较长，且航行体出水速度较快，认为在出水过程中相位近似一致，故周期对航行体出水姿态的影响较小。

2.4 出水相位对出水姿态参数的影响

在海浪运动中，浪和流是存在相对运动的，一方面，流体质点的运动速度和波浪的相速度是不同的；另一方面，波浪水质点运动方向和波浪传播方向在不同位置也存在差异。这会导致航行体在不同相位出水时，航行体出水姿态参数将会受到不同的影响。

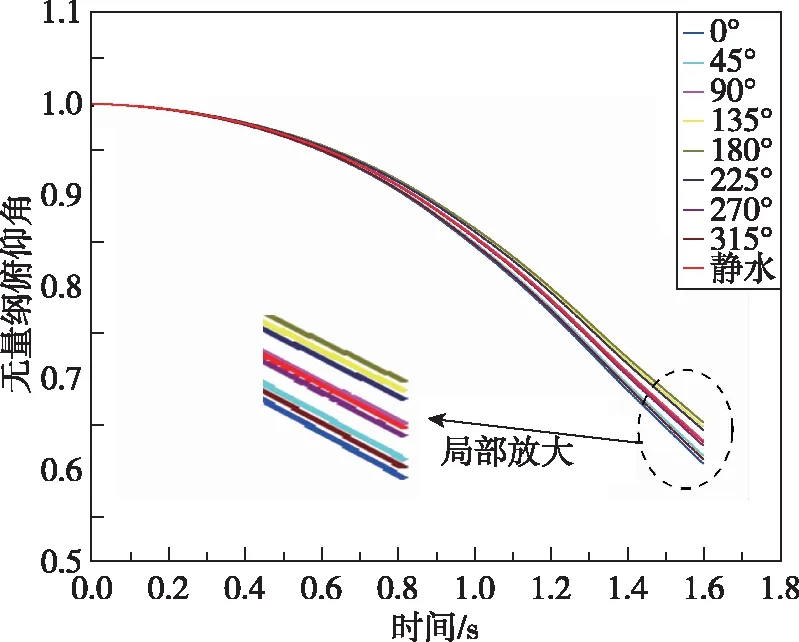
本节计算浪向取逆浪，波高取1.88 m，为了降低频率对时间的敏感度，周期取为100 s，从而可以近似认为初相位和航行体的出水相位相等；同时航行体出水速度快，认为头部和尾部出水时刻相位一致。即通过改变初相位来代替头尾出水相位的变化。工况选择中出水相位变化为0°～315°，间隔45°。出水姿态参数变化曲线如图12所示，无论是无量纲俯仰角还是无量纲俯仰角速度，其变化趋势与静水曲线是相同的，差别在变化幅度不同，观察图12两图的尾部放大曲线并结合一个周期内余弦曲线的形状，可以将尾部出水时刻的姿态参数大致分为3类：1)波峰范围(0°，45°，315°)，该位置出水对航行体的俯仰程度呈负影响，不利于发射成功；2)波谷范围(135°，180°，225°)，该位置出水对航行体的俯仰程度呈正影响，有利于发射成功；3)波节范围(90°，270°)，该位置出水时刻，波浪对俯仰参数的影响介于波谷和波峰位置。

(a) 无量纲俯仰角曲线

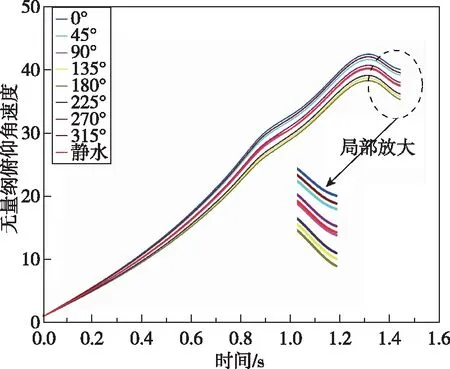
(b) 无量纲俯仰角速度曲线图12 出水相位对出水姿态参数的影响Fig.12 Influence of water-exiting phase on water-exiting attitude

出水相位对出水俯仰角和俯仰角速度偏差的影响如图13所示。图13(a)中，分界线以下的部分为对无量纲俯仰角的负影响，不利于发射成功；以上部分为对无量纲俯仰角的正影响，有利于发射成功。图13(b)中，分界线以上的部分为对无量纲俯仰角的负影响，不利于发射成功;以下部分对无量纲俯仰角的正影响，有利于发射成功。可以发现，两图中的偏差图线近似为余弦曲线，与规则波浪的波形近似，这是因为流体(波浪)质点和波浪的传播存在相对运动，流体质点运动速度的方向随着波浪相位的改变而发生改变。通过图13可以发现，在该计算工况下，俯仰角偏差变化随着出水相位呈余弦变化规律，因为随着出水相位的变化，流体质点的轨迹速度也发生改变，流体质点和波浪的传播存在相对运动，受到波浪相位的影响，流体质点运动速度的方向近似呈余弦变化。浪流的相对运动如图14所示，在波峰位置，波浪传播方向和流体质点的运动方向是相同的；在波谷位置，波浪传播方向和流体质点的运动方向相反。波峰位置和波谷位置浪流相对运动的不同，造成两个相位下航行体尾部触水无量纲俯仰角相反的情况：波峰位置出水，流体质点始终沿着轴正方向运动，此时弹体所受的附加惯性力偏向于航行体俯仰方向，波浪对尾部触水无量纲俯仰角的负影响达到最大；波谷位置出水，流体质点会沿轴负方向运动，此时弹体所受波浪的附加惯性力对航行体俯仰运动呈抑制作用，波浪对尾部触水无量纲俯仰角的正影响达到最大。

(a) 俯仰角偏差

(b) 俯仰角速度偏差图13 出水相位对出水姿态偏差的影响Fig.13 Influence of water-exiting phase on water-exiting attitude deviation

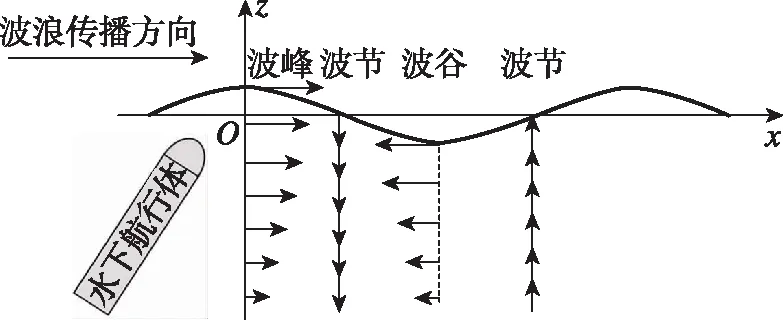
图14 浪流相对运动Fig.14 Relative motion of waves and fluid particles

波浪对水下航行体的作用力可分为两部分：1)由波浪压力场及流场引起的压差力； 2)由于波浪质点的轨迹速度引起的附加惯性力。浪级主要影响波浪力幅值的大小，对航行体出水姿态参数有着直接影响。而浪级、初相位和周期主要影响波浪质点的运动方向，改变附加惯性力，进而对出水姿态参数产生影响(或负影响)。因此，出水相位(近似初相位)的改变对出水姿态的影响主要体现在改变了波浪质点与航行体的相对运动，进而改变了附加惯性力的作用，通过与压差力共同作用，最终影响了航行体的出水姿态参数。

3 结论

本文通过边界元计算方法实现了对水下航行体水下发射的数值模拟，分析了波浪参数(浪向、波高、初相位和周期)对出水姿态参数的影响，得到以下结论：

1)波高越大，对航行体出水的姿态参数影响越大，但浪向和出水相位影响波高对出水姿态参数的影响效果。

2)周期对航行体出水姿态参数的影响实际上是影响了航行体水下航行阶段过程波浪的相位变化，进而改变了航行体出水时刻的相位。随着周期增大，频率对时间的敏感度减小，周期对航行体的出水姿态参数的影响逐渐减小。但在实际工程中波浪周期较长，航行体出水为瞬态，认为整个出水过程相位一致，可以不计周期对航行体出水姿态的影响。

3)出水相位主要通过改变波浪水质点与航行体的相对运动影响出水姿态。逆浪时，波浪传播和水质点运动同向的波峰位置对俯仰程度的负影响最大，不利于发射成功；波浪传播和水质点运动反向的波谷位置对俯仰程度的正影响最大，有利于发射成功；波节位置对俯仰程度的影响介于波峰和波谷位置之间。