超低轨卫星气动力辅助轨道控制研究
2022-09-13张靖奕焦洪臣
张靖奕,王 悦,焦洪臣,王 涛
(1.北京航空航天大学宇航学院,北京 102206;2.中国空间技术研究院遥感卫星总体部,北京 100094)
0 引言
超低地球轨道是指平均轨道高度低于450 km的地球轨道。相比于传统近地轨道卫星,超低轨卫星所处轨道高度更低,气动力带来的影响更为显著。如果仅将气动力视为阻力加以抵消,将忽略气动力作为轨道控制力的潜在用途。超低轨卫星的一个主要用途为对地观测,运行期间常期望卫星姿态保持对地稳定。因此,如何合理利用气动力,在辅助轨道控制的同时减小对任务的不利影响需要更深入的研究。
现阶段,已成功发射的超低轨卫星均将气动力视为阻力,施加控制力进行补偿或抵消。Muzi等、Steiger等中给出的地球重力场和海洋环流探测(Gravity field and Ocean Circulation Explorer,GOCE)卫星的轨道控制器,利用离子推进器和冷气推进器两套推进系统补偿卫星受到的非重力加速度的干扰。然而冷气推进系统所能提供的推力十分微弱,因此并没有对轨道高度以外的其他轨道要素进行严格控制;Wertz等中NanoEye卫星利用8个喷气式推进器,提供轨道控制并用于补偿大气阻力。目前,针对超低轨卫星气动力辅助轨道控制相关的研究较少,陈明利用DS3V软件分析了典型的超低轨卫星气动力,并设计了基于Hill方程的轨道保持控制器。
本文将以运行在太阳同步轨道上的对地观测卫星为例,研究超低轨道卫星在稀薄气体环境下的气动力特性,在考虑大气旋转的条件下分析计算设计构型下的气动力,建立利用气动力辅助的轨道控制模型,在卫星姿态保持三轴对地稳定的前提下,实现轨道保持控制,保证任意纬度下卫星实际位置与标称轨道位置偏差在给定的范围内。
1 超低轨卫星气动力
1.1 大气阻力模型
超低轨卫星所处空间环境中的气体可以被视为自由分子流。分子流的力特性模型基于气体的分子动力学理论建立;分子流与物体表面的相互作用模型则利用流体相互作用系数进行简化。Maxwell和Niven认为气体与表面碰撞大体上可以分为两类:镜面反射和漫反射。在模型中假设漫反射调节系数为,则镜面反射的调节系数为1-,从而可以得到压力系数和剪切系数表达式
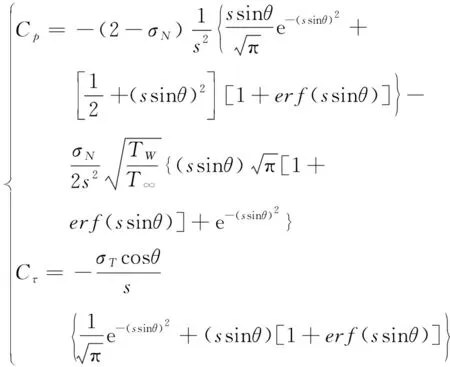
(1)

()=
1 000-640×e-00187 5(-120)(6 356766+120)(6 356766+)
(2)
式中,为以 km为单位的轨道高度。
如图1所示,在一般表面上定义以下量:表面法向量指向表面外侧,表面切向量=×(-×),入射角sin=-·。

图1 面元的法向和切向方向Fig.1 Pressure and tangential stress on each elementary surface area
将法向量、切向量带入压力和剪切系数表达式,可以得到力系数的表达式

(3)
式中,为参考面积,为迎流面积。
对于平板型物体,力系数即为压力和剪切系数在法向和切向的分量和,因此阻力系数和升力系数与入射角的关系为

(4)
在大气中运动的卫星受到的空气阻力加速度可以表示为
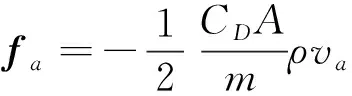
(5)
式中,为上面所求的阻力系数,为横截面积,为大气密度,为卫星相对大气的速度。
1.2 舵面产生的气动力
如图2所示,卫星基本构型包括本体与4个气动舵面,其中本体是一个端面为菱形的四棱柱体,菱形端面上有圆形进气口;四棱柱的每条棱上安装一个气动舵面,垂直地面的为垂直舵,平行于地面的为水平舵。当来流从正前方流向卫星时,垂直舵偏转产生垂直于轨道平面方向的力,即法向力,水平舵偏转产生指向地心方向的力,即径向力。
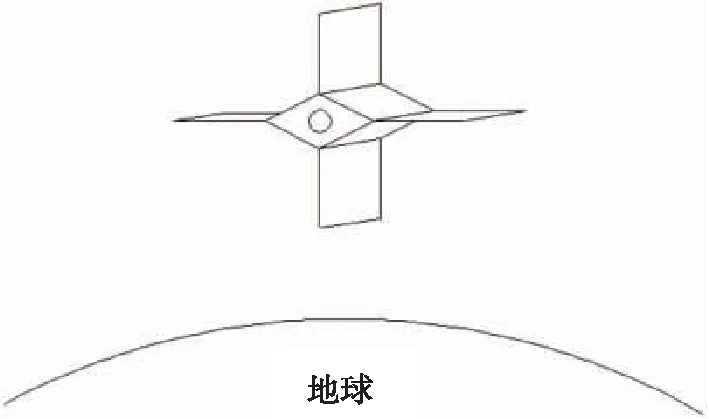
图2 卫星基本构型示意图Fig.2 Illustration of satellite configuration
对于舵面,常用角度为舵偏角。当卫星本体坐标系与轨道坐标系重合时,舵偏角与入射角的关系如图3所示。即当舵偏角为正时,=;当舵偏角为负时,=+180°。
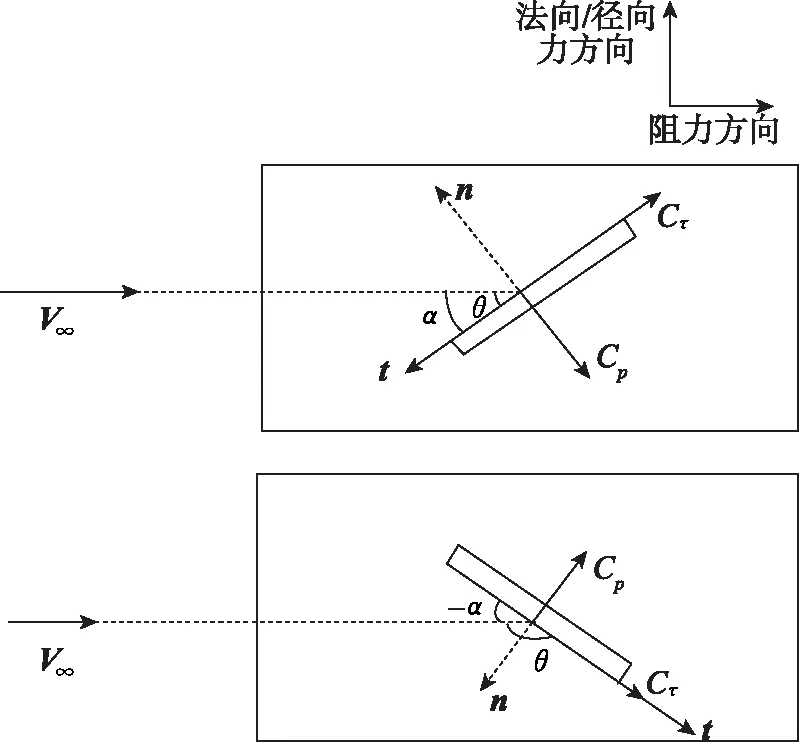
图3 舵偏角与入射角的关系Fig.3 The relationship between the angle of panel deflection and the angle of incidence
大气的旋转使来流方向不是卫星飞行的反方向,而是与之有一个微小角度偏差。以轨道平面为参考平面,定义来流攻角和侧滑角如图4所示,其中坐标系为卫星本体坐标系。

图4 来流攻角和侧滑角示意图Fig.4 Illustration of the angle of attack and the sideslip angle
对于轨道高度200 km的太阳同步轨道,一个轨道周期内来流攻角和侧滑角变化如图5所示。
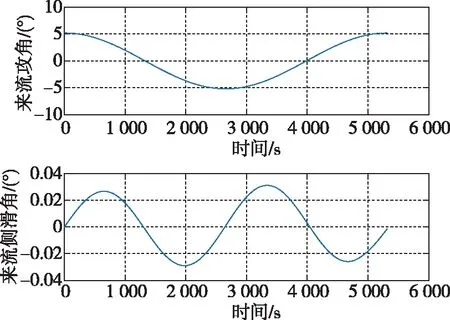
图5 来流攻角和侧滑角变化Fig.5 Change of the angle of attack and the sideslip angle
从图5中可以看出,来流侧滑角变化很小,可以忽略;而来流攻角变化较大,不能忽略。下面将对来流攻角导致气动舵受力的变化进行分析。
1.2.1 垂直舵
考虑大气旋转后,来流攻角、入射角和舵偏角的关系如图6所示。
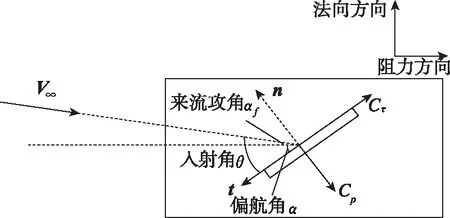
图6 来流攻角、入射角、舵偏角关系示意图Fig.6 The relationship between the angle of attack、the angle of incidence and the angle of panel deflection
舵偏角以顺时针旋转为正,则=+,因此垂直舵产生的法向力和阻力为
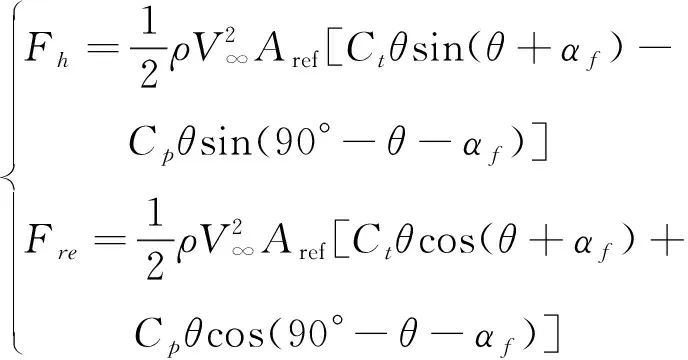
(6)
当存在来流攻角时,垂直舵不偏转也会产生阻力和法向力。阻力可以用推进器产生的推力抵消,然而法向力会影响轨道要素的变化,因此当不需要垂直舵产生控制力时,需令垂直舵的舵偏角等于来流攻角,即令垂直舵平面平行于来流,以降低垂直舵气动力对控制的影响。
当来流攻角在-5.5°~5.5°变化时,垂直舵偏转产生的最大/最小法向力及对应舵偏角变化如图7、图8所示。
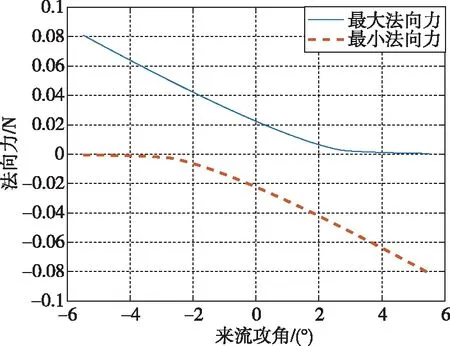
图7 垂直舵产生的最大/最小法向力随来流攻角的变化Fig.7 The maximum/minimum normal force generated by the vertical panels varies with the angle of attack
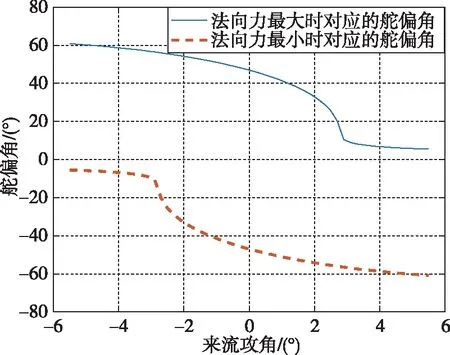
图8 垂直舵舵偏角随来流攻角的变化Fig.8 The angle of panel deflection of vertical panels varies with the angle of attack
从图8可以看出,不同来流攻角下,垂直舵产生最大/最小法向力对应的舵偏角不同,因此需要根据卫星在轨道上的位置来确定相应的舵偏角。
从图7可以看出,当来流攻角超过3.4°时,无论舵面如何偏转,来流速度法向分量为负,几乎不会产生正向的法向力;当来流攻角小于-3.4°时,无论舵面如何偏转,来流速度法向分量为正,几乎不会产生负向的法向力。设升阻比对应角度为,则来流攻角与的关系如图9所示。
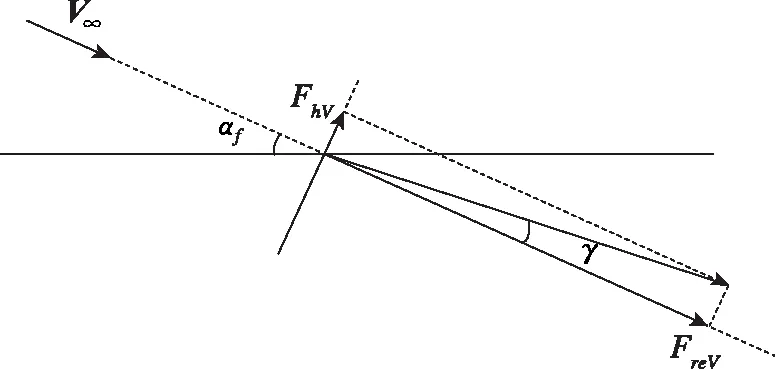
图9 来流攻角与升阻比对应角度的关系Fig.9 The relationship between the angle of attack and the corresponding angle of lift-to-drag ratio
因此,当<时才能产生正向控制力,当>-时才能产生负向控制力。由于来流攻角的影响,垂直舵产生的气动力能作为控制力辅助轨道控制的条件变得更加严格。
1.2.2 水平舵
对于水平舵而言,来流攻角的存在导致面元的切向与轴不重合,因此切向力会在法向(轴方向)产生分量。随着水平舵的偏转,法向分量会越来越大。水平舵偏转时产生的径向力可以用来辅助轨道控制的控制力,但随之产生的法向力会对轨道要素产生不可控的影响。如图10所示,当来流速度法向分量为负且需要正向控制力时,水平舵产生的法向力是阻碍控制的力,会使控制效果更加微弱,甚至会导致轨道要素反向变化;当来流速度法向分量为负且需要负向控制力时,水平舵产生的法向力是增强控制的力,让控制效果变得更好。

图10 水平舵受力示意图Fig.10 Illustration of the force generated by the horizontal panels
2 轨道控制策略
2.1 气动力辅助的控制策略
摄动加速度的轨道要素变化如下
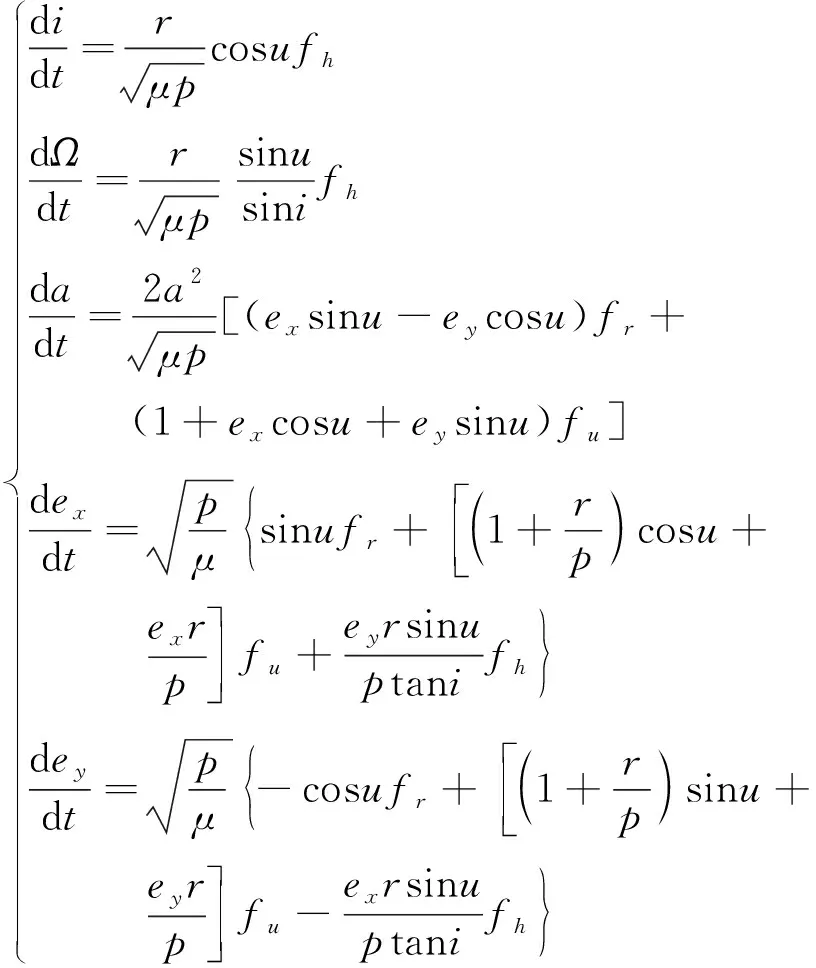
(7)
式中,控制力在轨道坐标系中定义,径向力产生的径向加速度沿地心距矢量的方向,迹向力产生的迹向加速度的方向垂直于矢量指向前方,法向力产生的法向加速度沿动量矩的方向。
根据式(7)的前两项,轨道倾角和升交点赤经只与法向加速度有关,所以法向力主要用来控制轨道倾角和升交点赤经。
利用平根估算法得到平根,与目标平均轨道要素对比,考虑卫星在轨道上的位置,即纬度幅角,控制分为9种情况,详见表1(为舵面产生法向力的大小,单位为N;单位为N)。
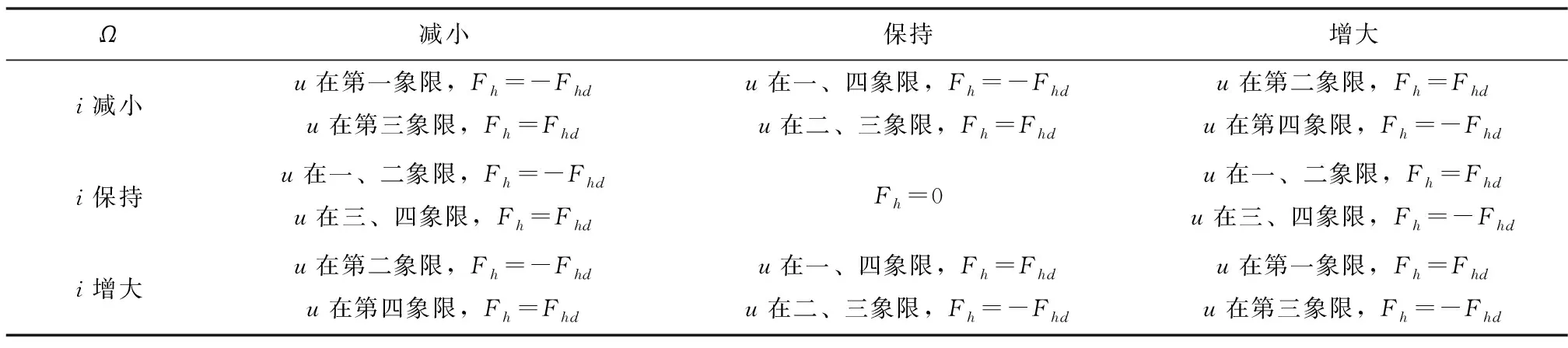
表1 控制轨道要素i,Ω所需法向力Tab.1 Normal force to control inclination and right ascension of ascending node
根据式(7)的后两项,考虑利用径向力控制偏心率。利用平根估算法得到平根,与目标平均轨道要素对比,考虑卫星在轨道上的位置,控制分为以下9种情况,详见表2(为舵面产生径向力的大小,单位为N;单位为N)。

表2 控制轨道要素ex,ey所需径向力Tab.2 Radial force to control eccentricity
根据前面的分析,只用于半长轴的控制,因此推力只与卫星整体所受阻力有关。当半长轴小于目标半长轴时,所需推力大于阻力;当半长轴大于目标半长轴时,所需推力小于阻力即可。推力的选择具有一定的范围,在范围内的推力值都可以让轨道要素向目标轨道要素变化。因此可以根据轨道要素的变化情况选择不同大小的推力,也可以选择一个较大的、可以满足所有情况的恒定推力。
考虑平根估算法得到的平根存在振荡、测量误差及噪声干扰等问题,需对各轨道要素设置误差容限,尽可能减小上述问题带来的干扰,避免控制抖振和频繁开关。此外,误差容限不能过大,否则会导致控制精度下降。因此,误差容限是两方面折中的结果。
半长轴的误差容限设置如图11所示。当初始半长轴小于等于目标半长轴时,施加最大推力直至到达误差上限;当初始半长轴大于目标半长轴时,不加推力直至达到误差下限。此后,当半长轴小于误差下限,施加最大推力直至达到误差上限,然后改用比阻力略小的推力直至半长轴达到误差下限,不断循环。因此,Δ需要大于平根估计结果中半长轴的振荡幅值。
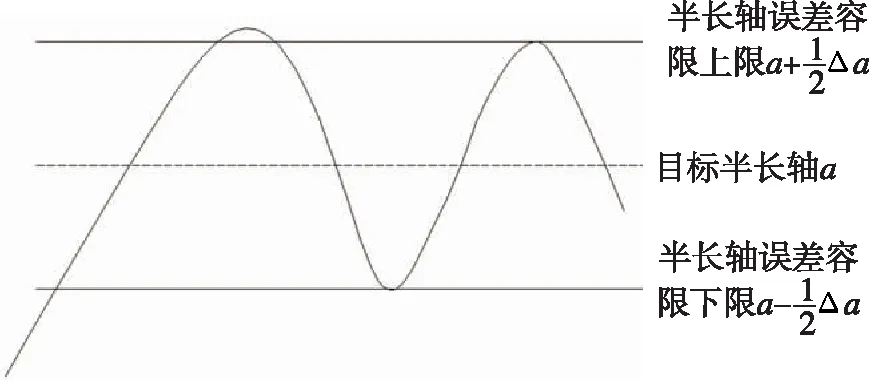
图11 半长轴误差容限Fig.11 The error tolerance of semimajor axis
其他轨道要素的误差容限设置如图12所示。当轨道要素小于误差下限,施加正向控制直至达到目标轨道;当轨道要素大于误差上限,施加反向控制直至达到目标轨道。因此,Δ(=,,,)需要大于平根估计结果中振荡幅值的2倍。
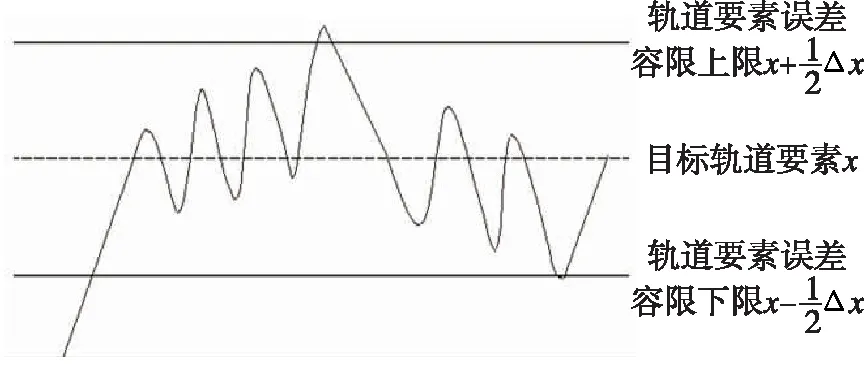
图12 其他轨道要素误差容限Fig.12 The error tolerance of other orbital elements
根据一天内平根估计算法得到的平根振荡幅值,各轨道要素误差容限取值如表3所示。

表3 轨道要素平根振荡幅值及误差容限取值Tab.3 Oscillation amplitude of mean orbital elements and the range of error tolerance
2.2 控制策略优化
由于任务要求,运行期间卫星姿态角将始终保持在零姿态角,因此推进器只能提供迹向推力对轨道要素进行控制,其他方向的控制力将由气动舵产生的气动力提供。根据1.2节的分析,气动舵在产生所需方向的控制力的同时也会产生其他方向的气动力干扰控制。尤其是水平舵偏转产生的法向力,仅与卫星在轨道上的位置有关,无法控制。从式中可以看出,轨道倾角变化率dd∝cos×(),因此水平舵偏转产生的法向力会导致轨道倾角不断减小。为减小水平舵的影响,考虑去掉水平舵,利用推力同时控制半长轴和偏心率的变化。
利用平根估算法得到平根,,与目标平均轨道要素对比,考虑卫星在轨道上的位置,即纬度幅角,当半长轴小于或大于目标半长轴时,控制分别有9种情况,详见表4、表5。其中,为阻力的大小,单位为N;≥0,为推力与阻力之差,可根据实际情况调整,单位为N;在表格中未涉及的时间内,令=。

表4 控制偏心率所需迹向推力(半长轴小于目标半长轴)Tab.4 Trace thrust to control eccentricity

表5 控制偏心率所需迹向推力(半长轴大于目标半长轴)Tab.5 Trace thrust to control eccentricity
2.3 管道保持
管道保持即为控制任意纬度下卫星实际位置与标称轨道位置偏差,管道保持半径的大小可以衡量超低轨卫星轨道保持的能力。为精确描述管道保持的控制误差,定义空间误差变量=(,),代表标称轨道和实际轨道与参考平面(轨道坐标系中径向与法向组成的平面)交点之间的向量差,为空间误差的法向分量,为空间误差的径向分量,如图13所示。
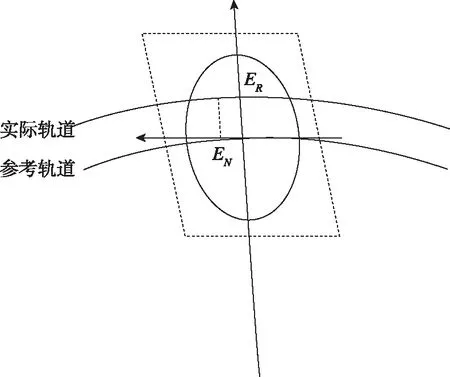
图13 空间误差示意图Fig.13 Definition of space error
设实际轨道要素与标称轨道要素之差为(,,,,),则管道半径法向、径向误差分别为
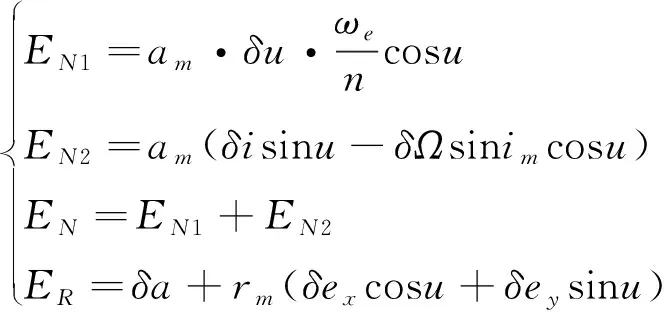
(8)
式中,下角标代表标称轨道的轨道要素,为标称轨道的轨道角速度,为地球自转角速度。
设半长轴偏离目标轨道的大小为,则偏心率偏离目标轨道最大值max=,因此(cos+sin)=,对于超低轨道≈,因此半长轴偏差与偏心率偏差对的影响效果基本相同。考虑到半长轴由推进器产生的推力进行控制,更容易且更准确,因此将14的管道径向误差分给半长轴误差容限Δ,将34的管道径向误差分给偏心率误差容限Δ,Δ。即当给定管道径向误差最大值时

(9)
利用上述关系,可以在给定管道保持径向误差的条件下,确定相应的轨道要素误差容限,从而将卫星实际位置保持在标称位置附近。
3 仿真校验
以运行在轨道高度196.939 km的太阳同步轨道上的卫星为例,仿真验证所设计的轨道控制策略的有效性。
取轨道要素误差容限Δ=Δ=0005°,管道径向误差最大值=2 000 m,采用推力控制半长轴、水平舵控制偏心率的控制策略,仿真时长为5 d,卫星轨道要素及管道偏差变化如图14所示。其中,轨道要素中蓝色实线代表卫星实际轨道平均根数,红色虚线代表目标轨道平均根数,红色双划线代表误差容限的上下限。
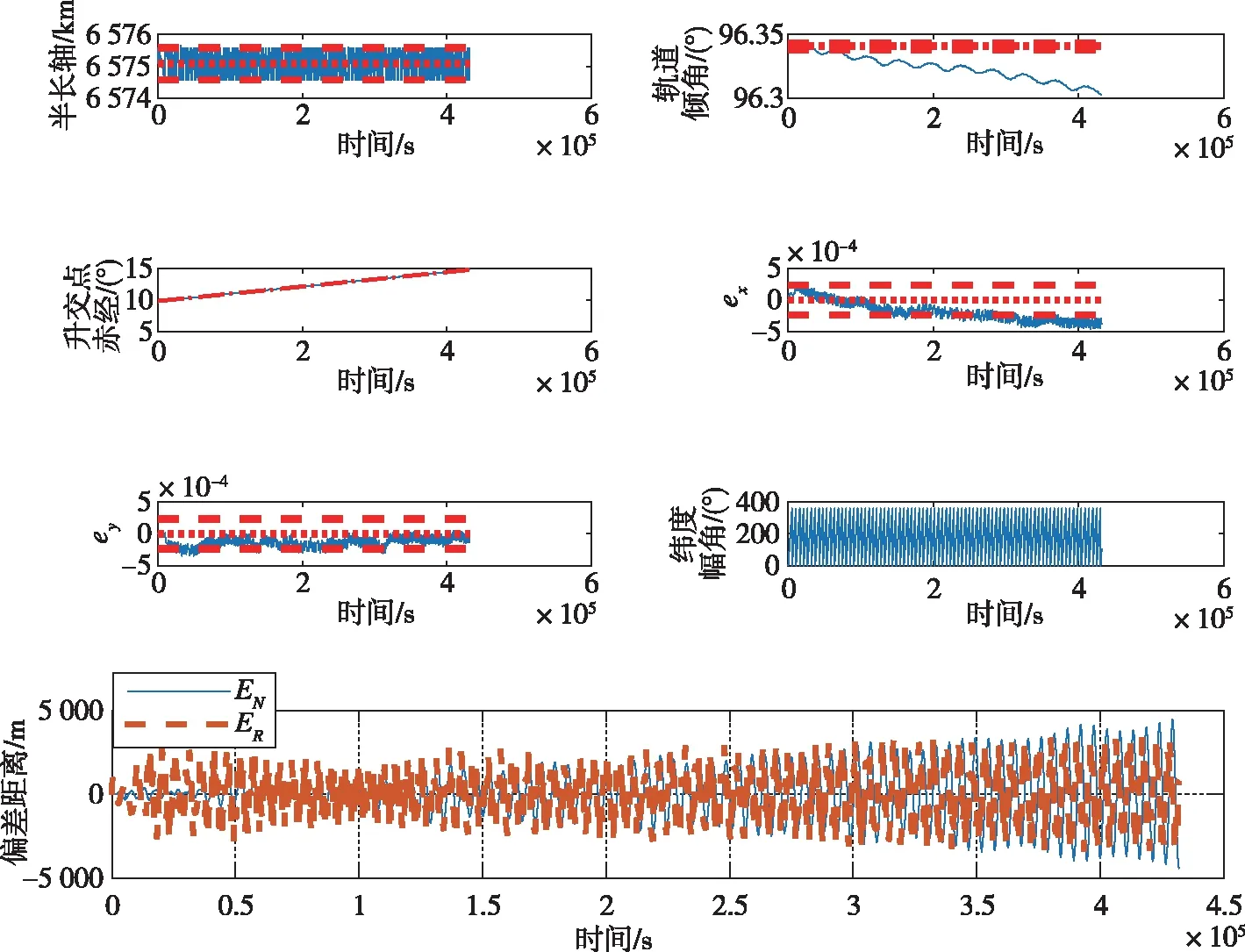
图14 轨道要素变化及管道偏差Fig.14 Changes of orbital elements and tube radius error
水平舵产生法向力的影响导致轨道倾角不断减小,因此管道偏差距离不断增大。
采用推力同时控制半长轴和偏心率的控制策略,卫星轨道要素及管道偏差半径变化如图15所示。
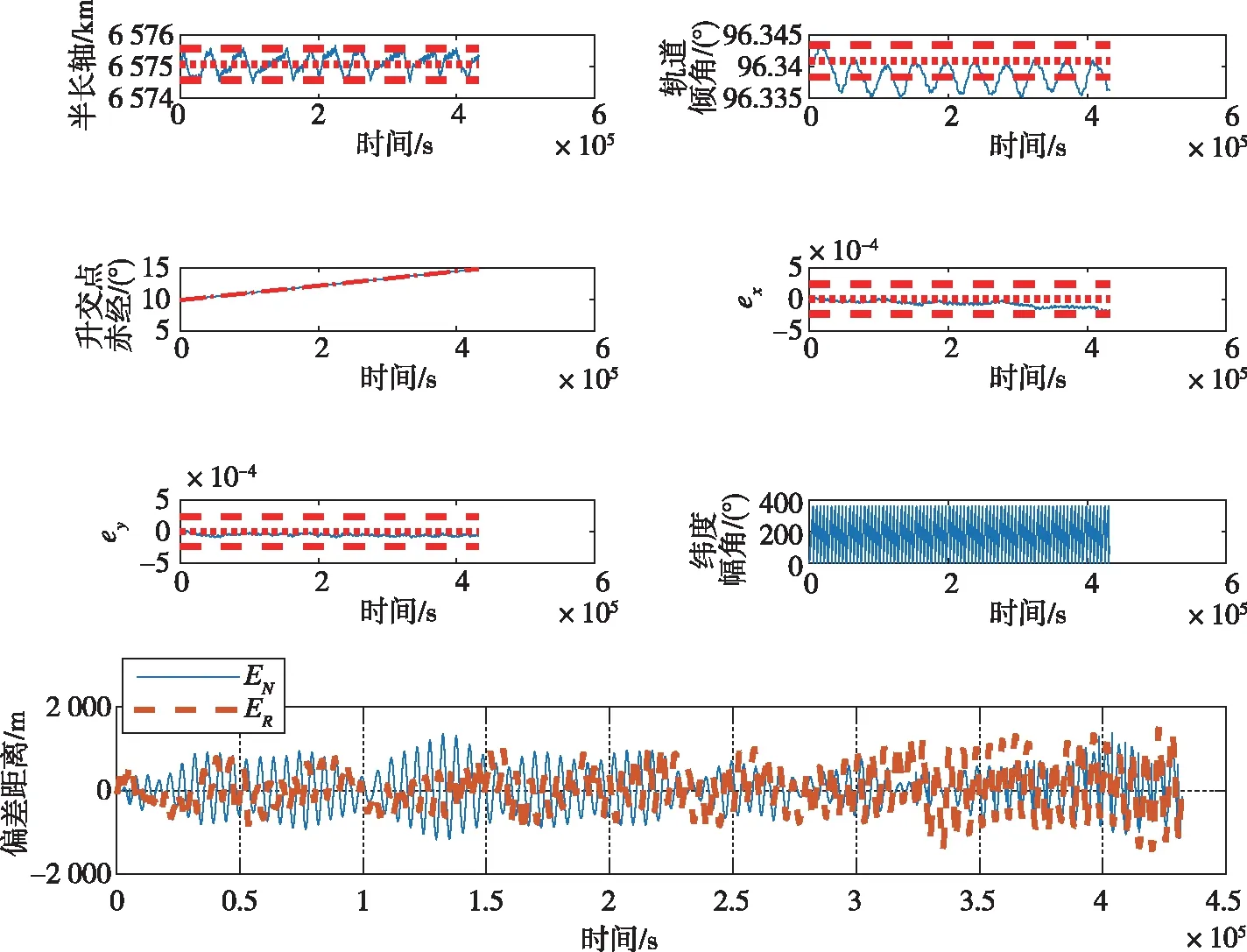
图15 轨道要素变化及管道偏差Fig.15 Changes of orbital elements and tube radius error
使用优化后的控制方法,轨道要素可以更好地维持在误差容限范围内,管道偏差也可以维持在给定的误差最大值以下。
4 结论
对于运行在太阳同步轨道上的超低轨卫星,本文给出一种利用气动力辅助的轨道控制方法,在卫星姿态保持三轴对地稳定的前提下,利用此方法可以实现轨道保持控制,保证任意纬度下卫星实际位置与标称轨道位置偏差距离在给定的范围内。文中给出的仿真实例说明了该方法的有效性。
