基于不等权向量角设计的有效剂量置信带构建

程 昕 蔺 杉

（东北师范大学 数学与统计学院，吉林 长春 130024）

一、引言

逻辑回归在二分类反应研究中具有广泛的应用。Piegorsch 和West 等[1]、Peng 和Robichaud 等[2]的定量风险和风险评估，以及Carter 和Chinchilli 等[3]、Frank 和Jason 等[4]的药物剂量反应曲线研究的一个关键目标是基于逻辑回归模型确定药物剂量水平和药物作用之间的关系。

关于单个有效剂量置信集的构造最早可以追溯到Fieller[5]和Cox[6]。Li 和Zhang 等[7]、Li 和Wong[8]分别提出了在贝叶斯框架下以及利用渐近理论和自举方法构建多维单个有效剂量置信带。

进一步地，研究者开始研究构建多个有效剂量的联合置信带。Al-Saidy 和Piegorsch 等[9]、Nitcheva 和Piegorsch 等[10]通过转化Scheffé 型联合置信带建立多个有效剂量的联合置信带。Li 和Nordheim 等[11]考虑用四种方法来计算多维有效剂量的置信区域。Tompstt 和Biedermann 等[12]在向量角度等权分配的情况下讨论了不同有效剂量个数和置信水平的组合会对临界值c 造成什么样的影响。本文在前人研究的基础上讨论向量角度不等权分配时是否会对临界值c 的结果产生影响，进而观察向量角度不等权分配时对有效剂量的定位效果是否优于向量角度等权分配。

二、有效剂量及联合置信带

将逻辑回归模型

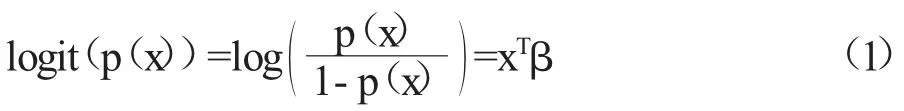
记为π（x）。其中，xT=（1，x1，…，xq）T=（1，xT），β=（β0，β1，…，βq）T是未知的参数向量，且p（x）=E（Y）。

记N 个响应变量分别为Yi，i=1，…，N，相应的协变量为xi=（xi1，…，xiq）T，利用极大似然估计来估计β，记为。假设有足够大的N，那么渐近结果是：

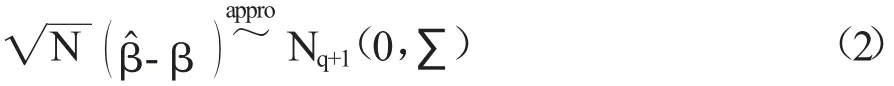
其中，Nq+1是q+1 维多元正态分布。0 是q+1 维零向量，渐近协方差矩阵∑可以用NJ-1估计，J-1是β^的观测协方差矩阵。因此，对于足够大的N，可以用NJ-1代替未知的渐近协方差矩阵∑。所以有近似分布结果：

于是，可以构建逻辑回归模型的联合置信带：

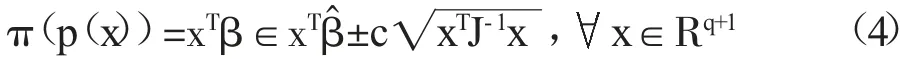
其中，c 是临界值，需要通过渐近分布结合置信水平1-α 求出。

定义如下的有效剂量为xp：

则有效剂量的双边型联合置信带为：

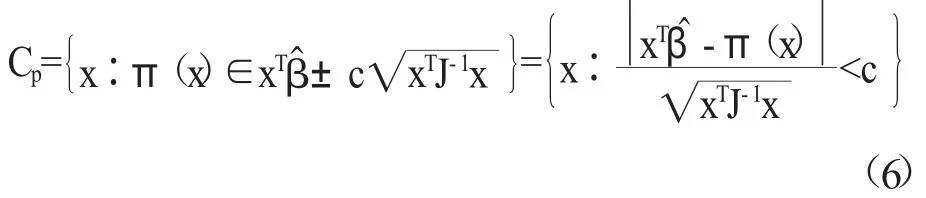
若选择适当的临界值c，则对于给定的k 值，Cpi的联合概率至少为1-α 。

对于k≥3，q=1，临界值c 满足：

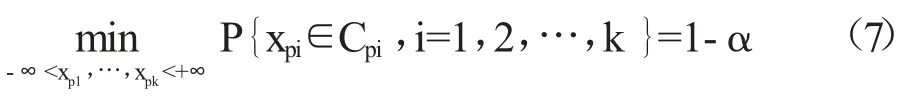
其中，-∞＜xpi＜+∞，i=1，2，…，k。当k=2 时，可以依赖于两个Zk的独立性求解临界值c。但是在k≥3 时不能利用独立性进行求解。令P2=J-1，根据公式（3），可以得到N=P-1- ）β ～N（0，I2）。定义N=（n1，n2）T的极坐标为（RN，θN），则有n1=RNcosθN，n2=RNsinθN。且RN≥，θN∈[0，2π）～U[0，2π），RN与θN相互独立。

公式（7）中的P ｛xpi∈Cpi，i=1，2，…，k ｝可以进行如下计算：

其中，V（xp）=表示与方向向量=PxP垂直并且与原点距离小于等于c 的N=（n1，n2）T 的集合。所以V（xpi）是一个2k 边的多边形区域。

设任意两个方向向量Pxpi和Pxpj的夹角为θij。如图1 所示，P（N∈Vk）等于平行四边形区域ABCD 的概率减去阴影区域的概率。即为：

其中l3（i）=

如图1 所示，以k=3 为例，计算P（N∈V3）。

图1 向量角度等权分配

具体计算步骤为：

步骤一：令V3旋转直到n2平分θ13，将旋转后的图形记为V3*，由于V3旋转后，P（N∈V3）的值不发生改变，所以N 在V3*中概率等于N 在V3中概率。

由图1 可以看出，四边形ABCD 是菱形。菱形ABCD 可表示为：

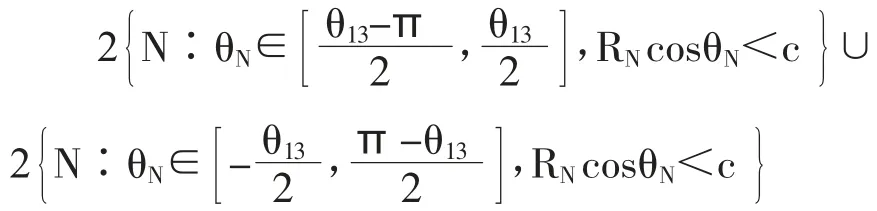
则菱形ABCD 的概率等于

步骤二：计算阴影部分的概率，由于左下角阴影部分与右上角阴影部分全等，所以只需计算右上角阴影部分。

阴影部分记为△PQB。接下来计算△PQB 的概率。直线PQ 的解析式为：

其中，l3（2）=

步骤三：用步骤一得到的菱形ABCD 的概率减去步骤二得到的阴影部分的概率的二倍即为P（N∈V3）。

其中l3（2）=

三、向量角的不等权设计与模拟

在此基础上讨论向量角度不等权分配是否会对临界值c 的结果有影响。将向量角度不等权分配分为两种情况，一种是向量角度渐近等权分配，另一种是向量角度渐远等权分配。将第一种情况记为AS2-1 型联合置信带，将第二种情况记为AS2-2 型联合置信带。将双边型联合置信带记为AS2 型联合置信带。图2-5 画出了有效剂量个数时向量角度渐近等权分配和渐远等权分配的示意图。图2 和图3 代表渐近等权分配情况，分别记为AS2-11 和AS2-12。图4 和图5 代表渐远等权分配情况，分别记为AS2-21 和AS2-22。其中，虚线表示向量角度等权分配。

图2 向量角度渐近等权分配（a ）

图3 向量角度渐近等权分配（b ）

图4 向量角度渐远等权分配（a ）

图5 向量角度渐远等权分配（b ）

模拟设计：由于主要讨论向量角度不等权分配时是否对临界值的结果产生影响，因此不考虑其他因素对临界值的影响。所以，首先假定有效剂量个数k=3。在渐近等权分布情况下，考虑θ12从左边趋近等权分配和从右边趋近等权分配两种情况，分别记为AS2-11和AS2-12；在渐远等权分布情况下，考虑θ12趋于零和趋于θ13两种情况，分别记为AS2-21 和AS2-22。在每种情况下，分别对三种角度进行模拟。在置信水平1-α =0.99、0.95、0.90 下，分别模拟10000 次。结果如表1、表2 所示。

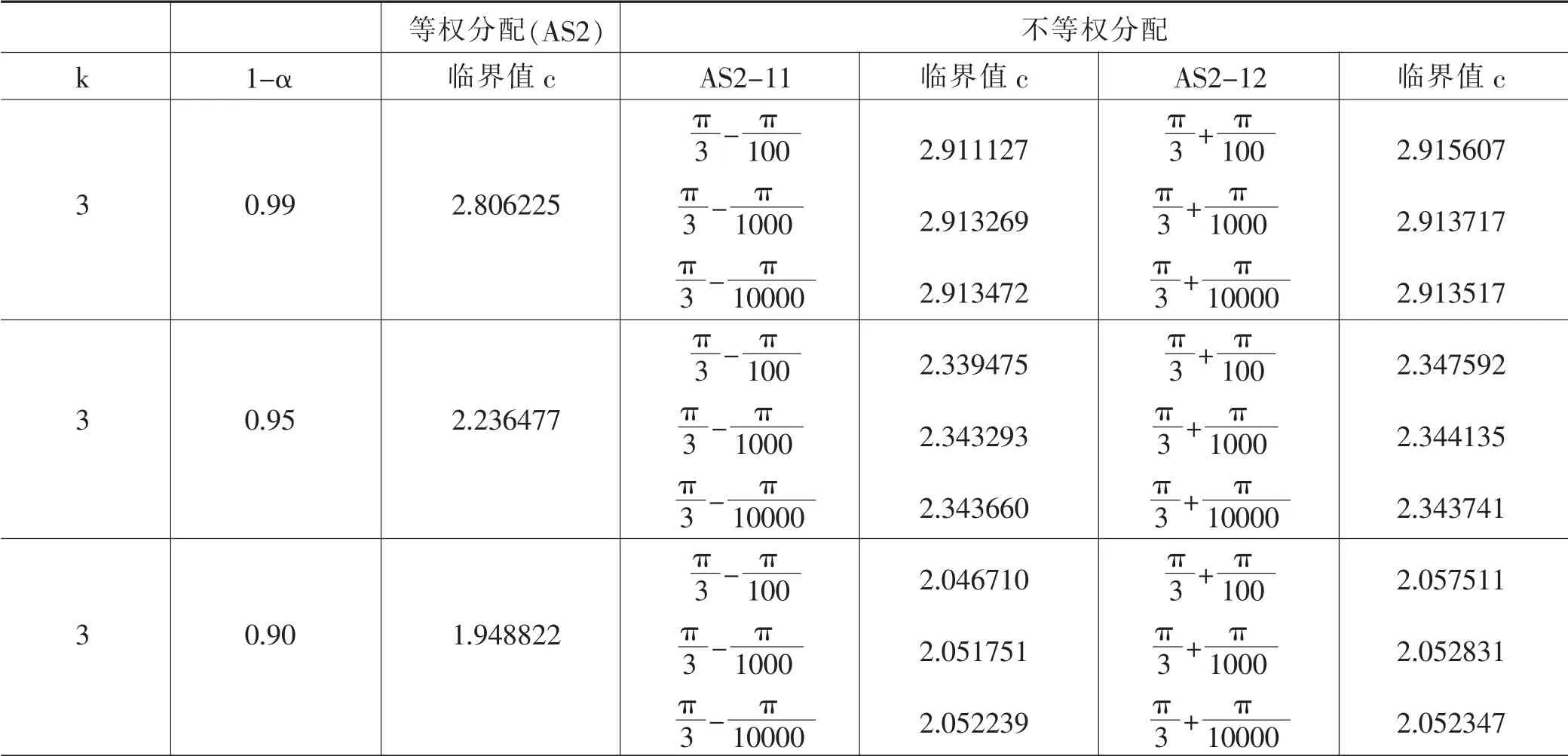
表1 AS2 型联合置信带与AS2-1 型联合置信带的临界值

表2 AS2 型联合置信带与AS2-2 型联合置信带的临界值

如果置信带的带宽越小，说明该置信带的效果越好，对有效剂量的定位就越精确。而置信带的带宽大小判断可以转化为临界值c 的大小判断。也就是说，临界值越小，该置信带对有效剂量的定位越精确。利用提升率公式来比较置信带的优劣，以双边型联合置信带为基准，将AS2-1 型联合置信带和AS2-2 型联合置信带与之进行比较。在1-α 置信水平下，相对于双边型联合置信带的提升率可以设为：

其中，c'表示向量角度不等权分配时的临界值，也就是AS2-1 型和AS2-2 型联合置信带的临界值；c 表示向量角度等权分配时的临界值，也就是AS2 型联合置信带的临界值。

根据提升率公式，得到表3、表4。

表3 AS2-1 型联合置信带的临界值提升率

表4 AS2-2 型联合置信带的临界值提升率

当有效剂量的个数k 和置信水平1-α 相同时，向量角度渐近等权分布时的临界值c 反而比等权分布时的临界值c 更大，说明渐近等权分布对有效剂量的定位没能更精确。向量角度渐远等权分布时的临界值c对等权分布时均有提升，且AS2-22 型提升的效果明显优于AS2-21 型。但是，在AS2-22 型的角度逐渐接近θ13的过程中可以看到，其提升效果是有限的，到达一定限度后，提升率不会再大幅增加。

四、结论

本文提出了双边型联合置信带向量角度不等权分配时，将向量角度不等权分配的情况分为两类，分别是向量角度渐近等权分配和向量角度渐远等权分配。其中，向量角度渐近等权分配又分为AS2-11 和AS2-12两种情况，向量角度渐远等权分配又分为AS2-21 和AS2-22 两种情况。通过模拟，对比向量角度等权分配的情况得出结论，向量角度渐近等权分配并不能使其临界值小于等权分配的临界值，但是向量角度渐远等权分配时可以获得相对等权分配时更小的临界值，即向量角度渐远等权分配时的双边型联合置信带对有效剂量的定位比向量角度等权分配时的双边型联合置信带更精确。并且，在渐远等权分配的两种情况下，AS2-22 情况有更明显地提升，但这种提升是有限度的。