基于SSA-LSTM 模型的消费者信心指数预测研究

2022-09-10李希亮陈亚娟

统计理论与实践 2022年8期

李希亮陈亚娟

（1.山东工商学院数学与信息科学学院，山东烟台 264005；2.山东工商学院统计学院，山东烟台 264005）

一、引言

消费是拉动经济增长的“三驾马车”之一，2011—2019 年消费对我国经济增长贡献率始终保持在50%以上，逐步成为中国经济增长的第一驱动力。2020 年受新冠疫情的影响，我国第一季度GDP 同比下降6.8%，对此各地政府出台多项政策以提高居民消费意愿，促进消费持续稳定增长。在反映消费意愿的众多经济指标中，消费者信心指数是当前最受社会关注的经济指标之一。消费者信心指数（Consumer Confidence Index，CCI）是体现消费者信心强弱的指标，是预测经济走向和消费变化趋势的先行指标。对CCI 准确且及时地预测有助于了解消费者消费倾向，对制定宏观经济政策和推动消费结构升级都有重大意义[1]。

我国获取编制CCI 数据的方法是问卷调查法，虽然编制方法在不断完善，但传统统计调查数据存在成本高、时滞性和低频性等问题，不能及时预测经济走势和了解人们消费心理变化。而网络搜索数据具有及时性和易获取等特点，本文结合网络搜索数据，使用深度学习方法预测CCI，从而解决CCI 数据发布的时滞性和低频性等问题。

关于CCI 预测的研究，早期学者多使用传统计量经济模型进行预测。陈雪娇（2011）使用ARIMA 模型预测我国CCI，发现ARIMA 模型具有良好的短期预测效果[2]。Lachowska（2013）结合网络搜索数据构建VAR模型对CCI 进行分析，发现构建的模型对个人消费支出短期的预测效果显著[3]。孙毅和吕本富等（2014）基于网络搜索数据构建多元线性回归模型，发现基于网络搜索行为预测的CCI 比宏观经济景气一致指数领先半年，且预测能力更强[4]。刘伟江和李映桥（2015）、董现垒和Bollen 等（2016）基于谷歌趋势数据，使用主成分分析方法合成变量并构建回归模型预测CCI，相较于传统预测方法，该模型拥有转折点预测能力[5-6]。传统计量经济模型对于平稳时间序列的预测效果较好，但对于呈现非线性、随机波动的时间序列，其预测效果较差，而CCI 与变量之间的关系复杂多样，因此一些学者提出采用机器学习或深度学习模型对CCI进行预测。刘苗和李蔚等（2018）基于百度搜索新闻文本数据，使用情感分析、机器学习等方法建立消费情感指数，发现消费情感指数和CCI 存在较高的相关性，且消费情感指数对短期消费趋势判断更灵敏[7]。邹鸿飞和王建州（2019）加入差分灰狼算法（DEGWO）改进误差反向传播（BP）神经网络模型对CCI 进行预测，结果表明组合模型相较于原模型预测精度显著提高且对CCI 变化规律的把握更准确[8]。唐晓彬和董曼茹等（2020）结合网络搜索数据，采用LSTM模型对我国CCI进行预测，同时引入SVR 模型、BP 模型以及XGB 模型等进行对比分析，结果表明加入网络搜索数据可以提高模型的预测精度，且LSTM 模型的预测效果显著优于其他预测模型。孙景和朱建霖等（2021）以网络搜索数据和网络新闻文本数据为依据，使用滑动时间窗口动态筛选预测变量，最终得出使用网络数据构建的机器学习预测模型预测精度较高且更为及时[9]。

梳理现有文献可以发现，结合网络搜索数据，运用机器学习或深度学习方法预测CCI 准确率更高，且LSTM模型预测的精确度和稳定性显著优于其他模型[10-12]，因而本文采用LSTM 模型，结合网络搜索数据对CCI 进行预测。但是，LSTM模型的预测精度较大程度依赖于模型参数的优化和选择，人为调整参数存在主观性和不确定性，难以确保模型参数的最优性。SSA算法稳定性高、收敛速度快、全局搜索能力强，且能够快速寻找到全局最优值[13]，因此本文引入SSA 对LSTM模型参数进行自动寻优，以期提高模型的预测效果。

二、模型与方法

（一）L a sso 回归

Lasso（Leastabsoluteshrinkageand selection operator）[14]通过构造一个惩罚函数将相对不重要的特征变量回归系数压缩到零，保留重要的特征变量，从而达到筛选变量的效果。Lasso 回归对数据类型设限较少，且能够弥补逐步回归和最小二乘回归陷入局部最优估计的不足，防止特征变量较多导致模型过拟合的情况。Lasso 回归的目标函数为：

（二）LSTM 模型

长短期记忆（Long Short-Term Memory，LSTM）[15]神经网络模型是一种特殊的循环神经网络（RNN），它能够解决RNN 存在的长期依赖问题和梯度消失问题。其记忆单元结构由细胞状态（Cell State）和3 个控制门（Gates）组成，3 个控制门分别为遗忘门（Forget Gate）、输入门（Input Gate）和输出门（Output Gate）。LSTM 记忆单元结构图如图1。

图1 LSTM 记忆单元结构图

LSTM神经网络由多个记忆单元组成，图1 是一个记忆单元。每个记忆单元对应处理某一时刻的数据。在t 时刻，记忆单元将对t 时刻的输入特征向量Xt、t-1 时刻的细胞状态Ct-1和t-1 时刻记忆单元的输出ht-1进行训练。三类数据将通过记忆单元的3 个控制门进行运算，计算过程如下：

首先，遗忘门决定将哪部分信息从细胞状态中丢弃。它根据t-1 时刻输出信息ht-1和t 时刻输入信息Xt决定需要删除的信息。遗忘门的控制函数为：

其中，ft、Wf、bf分别为遗忘门的门阀向量、权重矩阵和偏置向量，σ 为sigmoid 函数。

其次，输入门决定哪些信息需要进入单元状态中。输入门根据输入信息ht-1、Xt计算出需要保留下来的新信息it，并根据it计算出待更新的细胞状态t。输入门的控制函数为：

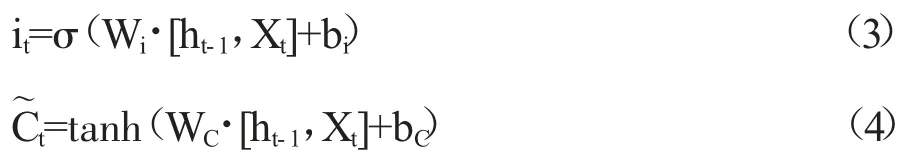
其中，it、Wi、bi分别为输入门的门阀向量、权重矩阵和偏置向量，t、WC、bC分别为待更新的细胞状态、权重矩阵和偏置向量，tanh 为激活函数。

然后，更新细胞状态。将t-1 时刻的细胞状态乘以ft，决定需要“遗忘”的信息，再将上一步中待更新的细胞状态t乘以it，决定“选择”哪些信息。细胞状态的更新函数为：

其中，Ct和Ct-1分别为细胞状态在t 时刻和t-1 时刻的对应值。

最后，输出门决定将哪些信息从细胞状态中输出。先由其计算输出结果ot，再由细胞状态处理，得到实际输出ht。输出门的控制函数为：

其中，ot、Wo、bo分别为输出门的门阀向量、权重矩阵和偏置向量，ht为t 时刻模型的输出值。

LSTM模型作为一种改进的RNN 模型，具有深度挖掘数据信息的能力，相较于传统方法，其计算能力更强，算法模式更先进。但LSTM模型的预测精度较大程度依赖于模型参数的优化和选择，人为调整参数存在一定的主观性和不确定性，难以确保模型参数的最优性，且耗时长，因此引入优化算法对LSTM 模型的参数进行自主寻优，既能得到最优的模型参数，又能节省人为调整参数的时间。

（三）麻雀搜索算法

麻雀搜索算法（Sparrow Search Algorithm，SSA）[16]是一种新型的群智能优化算法，受麻雀的觅食行为和反捕食行为的启发而得。在觅食过程中，麻雀种群分为发现者和跟随者，发现者负责探索觅食区域和方向，跟随者追随它们来获得食物。当麻雀种群察觉到周围存在捕食者时，会发出危险信号，并做出反捕食行为。麻雀不断寻找最好食物的过程就是寻找最优解的过程。

假设麻雀种群数量为N，将其放到D 维的搜索空间中，第i 只麻雀在空间中的位置为：xi=[xi，1，xi，2，…，xi，j，…，xi，D]，其中i=1，2，…，N，j=1，2，…，D。

在每次迭代的过程中，发现者的位置更新公式为：

其中，Xi，j表示第i 只麻雀在第j 维空间中的位置信息；α 是一个取值范围为（0，1]的随机数；t 和itermax分别为当前迭代次数和最大迭代次数；R2表示预警值，取值范围为[0，1]；ST 表示安全值，取值范围为[0.5，1]；Q 是服从正态分布的随机数。L 为1× d 阶的矩阵且所有元素均为1。

跟随者的位置更新公式为：

其中，Xworst和XP分别为当前全局最差位置和当前发现者所占据的最优位置。A 为1×d 阶的矩阵，其中每个元素随机赋值为1 或-1，且A+=AT（AAT）-1。

在模拟实验中，假设麻雀种群中有10%—20%的个体能察觉到危险，它们的初始位置是随机生成的。其位置更新公式为：

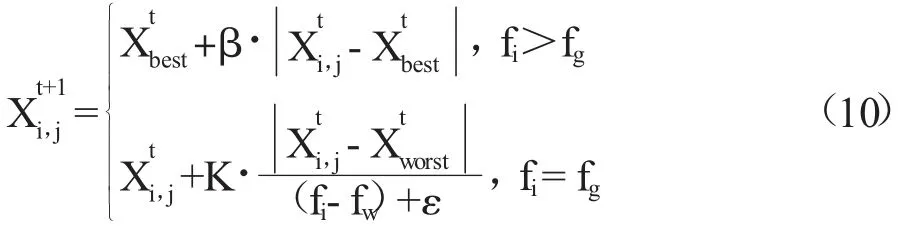
其中，Xbest为当前全局最优位置；β 和K 是控制步长的参数且均为随机数，其中β ～N（0，1），K 的取值范围为[-1，1]；ε 是使分母不为零的最小常数；fi为当前个体的适应度值，fg和fw分别为当前全局最佳和最差的适应度值。

（四）算法流程

SSA-LSTM预测模型的算法流程如下：

1.将原始数据分成训练集和测试集，进行归一化处理。

2.将LSTM模型中的超参数（时间窗口大小、隐藏层单元数目、学习率）作为优化对象。

3.SSA 相关参数初始化并设定需优化超参数的范围，确定最大迭代次数。

4.计算初始种群的适应度值并进行排序，找出最优和最差的适应度值。

5.更新发现者的位置、跟随者的位置和察觉到危险的麻雀的位置。

6.获取当前最优值，如果优于上一次迭代的最优值，则进行更新操作，否则不更新；继续进行迭代直到满足条件为止，最终得到全局最佳的适应度值和全局最优解值。

7.将SSA 得到的最优超参数构建LSTM 模型，对训练集进行训练并对测试集进行预测。

8.将测试集的真实值和预测值进行反归一化处理，使用不同的评价指标对模型的预测性能进行评估。

三、实证分析

（一）选取关键词

1.数据来源。本文的中国CCI 数据来源于中国经济信息网，选取时段为2011 年1 月至2021 年12 月。在近些年我国经济形势整体平稳运行的背景下，为了更加细致地刻画CCI 变化的动态过程，本文对月度数据进行三次样条插值处理，将月度数据扩充为旬度数据。

截至2021 年12 月，百度在我国搜索引擎市场份额中占比高达85.48%，其中PC 端占比为52.32%，移动端占比为94.72%，由百度提供的网络搜索数据（百度指数）能涵盖我国绝大部分网民的检索信息，所以本文采用百度指数作为网络搜索数据来源。网络搜索关键词PC 端和移动端的日度数据来源于百度指数官网，可用python 程序爬取获得，选取时段为2011 年1月1 日至2021 年12 月31 日，将关键词日度数据进行加总平均转换为旬度数据。

2.关键词的选取。基于中国CCI 编制准则，参考相关文献，采用范围取词法和经验取词法从经济形势、生活状况、物价水平、就业、投资和购房六个方面获取初始关键词，并结合相关文献和搜索引擎拓展取词，最终选取与CCI 相关的182 个关键词构成初始关键词词库。初始关键词词库如表1 所示。

表1 初始关键词词库

（二）数据处理与变量筛选

1.数据预处理。第一步：缺失值处理。通过python爬虫获得的关键词百度指数日度数据，有个别关键词数据存在缺失值严重的情况，进行剔除处理。第二步：数据换频。本文将CCI 月度数据进行三次样条插值处理，转换为旬度数据，故需要将关键词日度数据进行加总平均转换为旬度数据。第三步：平滑处理。为了消除网络搜索数据的短期波动性，凸显数据的长期趋势，故对关键词旬度数据采取三期移动平均的平滑处理。

2.筛选关键词。采用传统统计方法筛选关键词，可剔除存在较大噪声的网络关键词数据，得到与CCI相关性较强的关键词。通过Pearson 交叉相关分析，取阈值为± 0.6，去除噪声大的数据，筛选出与CCI 相关性较强且对应滞后期大于零的关键词，获得26 个关键词。

3.确定预测变量。由上一步得到了与CCI 相关性较高的26 个关键词，但不同关键词在模型中的解释能力不同，有的关键词在模型中边际贡献较弱，需要剔除。采用Lasso 回归算法对以上26 个关键词进行降维，剔除解释能力较弱的关键词，从而获得最终的预测变量。

Lasso 回归模型中的λ 值是待确定的，通过正则化路径图可以确定λ 的取值范围，再结合交叉验证法确定λ 值。使用sklearn 模块中的LassoCV 类进行交叉验证，确定λ=0.0251。将最终的λ 值代入Lasso 回归模型，筛选得到5 个预测性能较优的关键词，分别是美元、电脑、房贷计算器、搜房网、链家。预测变量与CCI的相关系数和对应滞后阶数如表2 所示。

表2 预测变量与消费者信心指数相关性分析

由表2 可知，CCI 和自身1 阶滞后相关系数高达0.9949，呈显著正相关。为了增强模型的预测效果，将CCI 的1 阶滞后作为预测变量。最终预测变量中包含了三个购房方面的关键词，分别为房贷计算器、搜房网和链家，表明CCI 和购房方面的关键词相关性很高，说明消费者对房价和房源相关信息的关注度较高，购房信息会影响居民的消费意愿和信心。消费者对美元和电脑的搜索体现了对经济形势和物价水平的关注度。消费者根据自身的消费意愿和关注点，搜索相关信息，并基于相关信息对消费结构进行一定调整。从表2 可以看出，关键词电脑和搜房网与CCI 高度负相关，分别具有高31 阶和1 阶的滞后相关性。关键词美元、房贷计算器和链家与CCI 高度正相关，分别具有高22 阶、20 阶和25 阶的滞后相关性。

综上可得，最后的预测变量为CCI 滞后1 阶、美元滞后22 阶、电脑滞后31 阶、房贷计算器滞后20 阶、搜房网滞后1 阶和链家滞后25 阶，被预测变量为当期CCI，样本容量为363 期。

（三）建立预测模型与效果评价

1.归一化。先将数据划分为训练集和测试集，本文将最后36 期（一年）CCI 作为测试集预测对象。对数据进行归一化变换以消除不同变量之间的量纲差异对模型预测结果的影响。公式如下：

其中，xi、xmax、xmin、xi' 分别是变量X 中第i 个样本原始值、最大值、最小值和归一化后的数据，xi'取值范围为[0，1]。使用归一化后的数据构建模型，并将最终预测值进行反归一化变换得到实际预测值。

2.模型预测性能评价指标。为了对比SSA-LSTM模型和LSTM 模型的预测性能，本文采用拟合优度R2、均方根误差RMSE、平均绝对误差MAE、平均绝对百分比误差MAPE 四种指标对模型预测性能进行评价。指标定义公式如下：

3.预测结果分析。本文基于Python 3 语言环境和Pytorch 深度学习框架构建SSA-LSTM预测模型，该模型输入层的维度为6，分别为CCI 滞后1 阶、美元滞后22 阶、电脑滞后31 阶、房贷计算器滞后20 阶、搜房网滞后1 阶和链家滞后25 阶，输出层为CCI 的预测值。使用Adam 优化算法进行训练，激活函数为sigmoid 函数和tanh 函数，损失函数设定为均方误差（MSE），迭代次数设为500 次。通过SSA 算法寻优，得到的最优超参数分别为滑动窗口timesteps=7，隐藏层单元数目num_net=95，学习率η =0.005。将最优超参数带入LSTM模型，得到最后36 期（2021 年1 月上旬至2021年12 月下旬）预测结果，将预测结果进行反归一化处理，得到CCI 的预测值。CCI 预测结果图如下：

从图2 可以看出，SSA-LSTM 模型一年期预测效果显著，CCI 的预测值和实际值差距很小，充分利用了历史数据信息，且转折点预测能力较强。为了验证引入SSA 算法对LSTM 模型寻优效果更好，将其与LSTM基准模型进行对比，计算出预测性能评价指标，如表3 所示。

图2 S S A -LSTM 模型预测结果图

表3 测试集预测结果统计性能对比

由表3 可以看出，在对CCI 的一年期预测中，引入SSA 算法对LSTM模型参数进行自主寻优显著提升了模型的预测性能。具体而言，在预测效果方面，SSALSTM模型的拟合优度R2为0.9909 接近于1，相较于LSTM基准模型提高了2.57%，说明引入SSA 算法能有效提高LSTM模型的预测效果。在预测精度方面，SSALSTM 模型的RMSE、MAE、MAPE 明显小于LSTM 模型，与LSTM模型相比，SSA-LSTM模型的预测精度提高了0.12%，说明引入SSA 算法后LSTM模型的预测精度显著提高。SSA 算法之所以能够有效提高LSTM模型的预测性能，在于其稳定性高、收敛速度快、且全局搜索能力强，保证了预测结果的稳定性和准确性。

四、结论

本文针对CCI 的非线性时变特征，结合相关网络搜索数据，使用Lasso 算法进行合理降维，采用LSTM神经网络模型对CCI 进行预测，并引入SSA 算法进行参数寻优，构建SSA-LSTM 模型对CCI 进行预测研究。从最后筛选出的网络搜索关键词可以看出，消费者对经济形势、物价水平和房价情况等与人民生活息息相关的经济指标的关注度与CCI 高度相关。根据预测结果图可以看出，SSA-LSTM 模型具有很好的转折点预测能力。通过对比LSTM模型和SSA-LSTM模型的预测结果发现，引入SSA 算法的LSTM 模型预测效果和预测精度显著高于LSTM基准模型，预测效果和预测精度分别提高了2.57%和0.12%。同时，结合网络搜索数据的当月CCI 预测值在下月初即可获得，而官方当月CCI 在下月下旬才能获得，即基于SSA-LSTM模型结合网络搜索数据的CCI 预测值比官方发布数据领先半个月左右，其预测结果能够及时为市场调控提供参考依据。以上结果表明SSA-LSTM预测模型具有较优的预测效果和较高的预测精度，且预测结果比官方发布数据更为及时，是一种有效的CCI 预测模型。