全极化合成孔径雷达高维小样本数据在森林地上生物量估算中的应用
2022-09-08吴国明范文义司国玉于颖魏萌刘志会毛毓
吴国明 范文义 司国玉 于颖 魏萌 刘志会 毛毓
(东北林业大学,哈尔滨,150040) (河北省塞罕坝机械林场) (东北林业大学)
森林地上生物量是研究碳循环的重要指标[1],常用传统的实地调查法或依据遥感的方法进行估算[2]。实地调查法多由异速生长方程计算获得,遥感的方法对于区域的森林地上生物量估算至关重要[3]。
遥感的方法主要的数据源,通常为机载或星载的光学传感器、激光雷达、合成孔径雷达(SAR)等。光学遥感不具备穿透性,只能收集到冠层表面信息,无法表征波段树干信息。雨云的存在,也会影响光学遥感的应用[2]。然而,这些限制可以通过使用合成孔径雷达克服,它可以穿透树冠并与树枝、树干相互作用[4]。合成孔径雷达常用波段由短到长分别为X(波长37.5~25.0 mm)、C(波长75.0~37.5 mm)、L(波长300.0~150.0 mm)、P(波长1 300.0~300.0 mm)波段。长波长的合成孔径雷达卫星,通过穿透冠层覆盖层使信号直接作用于树干,从而使森林地上生物量可以进行更直接的测量[5]。多项研究表明,较长波长的L波段合成孔径雷达数据,在森林地上生物量估算中是有效的[1,6-7]。通常通过建立森林地上生物量和合成孔径雷达参数之间的经验关系的回归模型估计,包括后向散射强度或极化分解[4,7-9]。
高维小样本,是指数据集合中样本的特征维数远高于样本的个数[10]。随着极化合成孔径雷达图像处理技术的发展,越来越多的适用于森林的非相干极化分解方式被提出,如弗里曼(Freeman)分解[11]、山口(Yamaguchi)分解[12]、非负特征值(NNED)分解[13]等。虽然其中的分解方式在理论上存在一定的优化递进关系,但遥感数据源以及观测区域条件的不确定性,使得各分解方式之间不能完全替代,而引入更多的分解结果又会引起特征维度的增加,高特征空间规模的样本稀疏性使得绝大多数涉及统计学意义的建模方法都无法获得正确而有效的结果,产生“维数灾难”问题。此外,利用极化分解和后向散射系数构建特征集做森林地上生物量回归预测,还存在着特征变量具有高共线性的问题。虽然不同的极化分解方式是对图像以不同的方式进行解译,但分解的散射机制大体相同,三分量分解将散射机制描述为体散射、奇次散射、偶次散射[11-13],二分量分解将散射机制描述为冠层体散射、地面散射[14]。这导致了提取散射分量在统计学上有很大的相关性。
在回归模型中,影响模型效果的重要因素是样本量[15]。森林地上生物量的样本获取多依赖于传统的实地调查法[2],而获取大样本林业数据又会极大提高外业成本,所以林业数据的高维小样本是常见问题。对于大样本情况时估算森林地上生物量的研究成果较多[2,7-8,16];但如何利用以高共线性的极化合成孔径雷达数据为特征集的高维小样本数据,进行维数约简和参数回归,以提高森林地上生物量的估算精度,这方面的研究较少。
为此,本研究以河北省承德市塞罕坝机械林场为试验区域,设置37块实测样地;以随机森林模型、自适应遗传算法为基础,构建随机森林模型与自适应遗传算法的混合算法(RF-LOOCV-AGA),对高维小样本合成孔径雷达数据特征集同时进行特征选择和回归估计;利用试验地大地2号(ALOS-2)全极化数据提取121个高共线性特征,结合实测样地数据,构建高共线性高维小样本数据集,并应用随机森林模型与自适应遗传算法的混合算法、随机森林算法、逐步回归法,分析全极化合成孔径雷达数据估算森林地上生物量时,因样地较少、影响因素维数多存在的高共线性;探索在算法层面各极化分解参数之间存在的高共线性及小样本林业数据回归估计泛化能力;将3种算法进行对比分析,旨在为应用高共线性高维小样本林业数据估算森林地上生物量提供参考。
1 研究区域概况
本研究试验区域为塞罕坝机械林场,位于内蒙古高原的东南缘,地处内蒙古高原与冀北山地的交界处(42°22′~42°31′N,116°53′~117°31′E)。地形地貌组合为高原-波状丘陵-漫滩-接坝山地;林区属寒温带大陆性季风气候,气候由半湿润向半干旱气候过渡,年降水量490 mm、蒸发量1 230 mm,海拔1 010.0~1 939.9 m[17]。样地主要树种为白桦(Betulaplatyphylla)、椴树(Tiliatuan)、硕桦(Betulacostata)、华北落叶松(Larixprincipis-rupprechtii)、山杨(Populusdavidiana)、色木槭(Acermono)、油松(Pinustabuliformis)、云杉(Piceaasperata)、柞树(Quercusmongolica)、樟子松(Pinussylvestrisvar.mongolica)共计10个树种。
2 研究方法
2.1 数据来源
星载数据:本研究以一景覆盖塞罕坝机械林场的大地2号(ALOS-2)星载全极化合成孔径雷达数据作为遥感数据源,使用SNAP8.0软件对大地2号数据进行辐射定标、生成T3矩阵、精致李滤波(Refine-Lee滤波,9×9大窗口、3×3小窗口)、多视(4×9)和地理编码处理后,导入PolSARpro_v6.0.2中进行极化分解,提取相应功率值与后向散射系数;星载全极化合成孔径雷达参数:数据级别为HBQR1.1;成像日期为2020年8月8日15时20分;极化通道为全极化(水平同向极化(HH)、水平-垂直异向交叉极化(HV)、垂直-水平异向交叉极化(VH)、垂直同向极化(VV));距离分辨率为2.86 m;方位分辨率为2.78 m;纬度范围为41.904 1°~41.612 1°N;经度范围为116.952 6°~117.730 0°E。
样地数据:在星载数据覆盖的试验区内等间隔设置样地(见图1),使用实时动态测量仪对样地中心点进行定位,并对样地内数目进行每木检尺,获取其胸径、树高;单木生物量由异速生长方程计算获得。
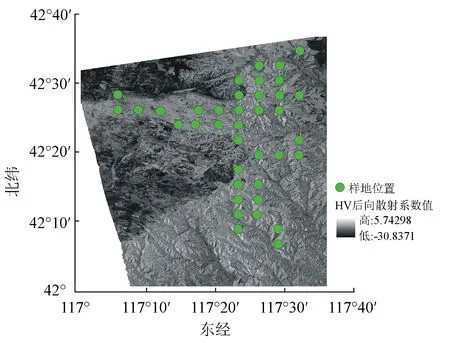
图1 样地位置示意图(背景为垂直-水平异向交叉极化(VH)后向散射系数图)
辅助数据:全球数字高程数据用于提取地形因子及星载大地2号数据的地理编码(见图2)。本研究采用ASTER GDEM V2 30m全球数字高程数据,数据来源于中国科学院计算机网络信息中心地理空间数据云平台。

图2 研究区域地形信息
2.2 高维高共线性影响因素提取
本研究采用后向散射系数与极化分解作为基础影响因素。已有研究表明,与单通道后向散射系数相比,经过各类变换构造的指数,比单一影响因素对植物生物量的敏感性更高[18],如,与生物量的相关性,σVH、σVV比σVH/σVV更好[19]。所以本研究在使用4种后向散射系数(σVH、σVV、σHH、σHV)以及弗里曼(Freeman)二分量分解[11]、安-杨(AnYang)三分量分解、非负特征值(NNED)三分量分解、弗里曼(Freeman)三分量分解[14]、范西尔(Van Zyl)三分量分解[13]、山口(Yamaguchi)三分量分解[12]、直推式支持向量机(TSVM)分解、“散射熵(H)-各向异性度(A)-平均散射角(α)”协同分解(H-A-α分解)、依据特征值的“散射熵(H)-各向异性度(A)-平均散射角(α)”协同分解、依据特征向量的“散射熵(H)-各向异性度(A)-平均散射角(α)”协同分解的各个散射分量作为影响因素之外,另经过各类变换构造后向散射系数指数(Iσ=σVH/σVV)、三分量极化分解指数(I3,V=V/(D+O)、I3,D=D/(V+O)、I3,O=O/(D+V),V为体散射分量、D为二次散射分量、O为表面散射分量)、二分量极化分解指数(I2,V=V/G、I2,G=G/V,G为地面散射分量)作为影响因素。
2.3 逐步回归法
参数约简是解决高共线性高维度小样本的重要方法,参数约简可分为特征抽取和特征选择两个方面[20]。特征抽取,是指在原始数据集中通过构造变换的方式,构建新的低维空间,其代表性的方法是主成分分析法。特征选择,是在原始特征空间中,根据某种检验结果,挑选一部分最优特征子集达到降维的目的。与特征抽取相比,特征选择不改变原始数据集的影响因素含义,仅仅通过筛选的方式剔除不相关或多余影响因素,使模型描述更加准确[21]。应用多元逐步回归方法构建模型,是将影响因素逐个引入模型中,对每个引入的影响因素进行显著性检验,保留显著影响因素;当引入的新影响因素使得原影响因素变得不再显著时剔除原影响因素,逐步回归获得最优模型;逐步回归作为一种同时进行参数约简与回归的方法得到了广泛的应用[22]。本研究将随机森林模型与自适应遗传算法的混合算法(RF-LOOCV-AGA),与被广泛应用于参数约简和参数拟合的逐步回归法进行对比。
2.4 随机森林算法
随机森林算法是集成多个弱学习器的集成算法,其基本单元是决策树,若干个决策树组成了随机森林算法。随机森林算法,主要利用自助重抽样方法从原始样本中抽取约66%的样本,对每个决策树进行训练;取所有决策树预测值的平均值作为最终的回归结果[23]。随机森林算法,不仅适用于回归和分类计算,也可进行特征排序与特征筛选。在随机森林中,利用每一颗决策树,使用自助重抽样没有抽到的约33%的数据计算它的误差,称为袋外误差(记为EOB,1);然后,随机地对袋外数据所有样本的特征加入噪声干扰,并再次计算它的袋外误差(记为EOB,2);设随机森林中有n棵树,则特征X的重要性为∑[(EOB,2-EOB,1)/n]。用这个表达式作为相应特征的重要性的度量值,是因为若给某个特征随机加入噪声后,袋外的准确率大幅度降低,则说明这个特征对于样本的分类结果影响很大,重要程度比较高,由此可以获取特征的重要性排序,按照此排序去除重要性较小的影响因素即可完成特征选择。
2.5 随机森林模型与自适应遗传算法的混合算法构建
随机森林模型与自适应遗传算法的混合算法(RF-LOOCV-AGA)的基础框架,依据自适应遗传算法;遗传算法是一种随机搜索算法,可模拟自然生物的自然选择和进化。与传统的搜索算法(例如二分法、斐波那契、牛顿法)相比,遗传算法具有很高的鲁棒性,并且能够解决高度复杂的非线性问题[24]。该算法模仿生物学中简单染色体的双螺旋编码,以二进制数据结构对自变量集进行编码,并对该结构进行重组运算以保留关键信息[25]。通过算法本身不断地进行交叉变异,最后接近最佳的解决方案。
遗传算法本质上属于求解极大值或极小值的优化算法;所以进行初始特征选择后,依然要有一个明确的数值作为优化目标,并将其定义为适应度。对于估算森林地上生物量的模型,最重要的指标是模型的均方根误差、决定系数,均方根误差越小则模型的相对偏差越小,决定系数越大则模型的计算精度越高。由于高维小样本数据特征数(121个)远大于样本数(37个),所以即使在种群中筛选掉一部分特征影响因素,筛选后的影响因素数目仍然有很大概率会大于样本数。统计学公认的原理是:即便在模型中加入与评价指标无关的影响因素,决定系数依然会增加而不是减小;当特征数大于样本数时会导致决定系数无限接近于1,所以利用决定系数控制遗传算法达到最优解是错误的选择。小样本数据面临的最大问题,是在进行回归估计时,由于样本在特征空间的稀疏性导致拟合模型将噪声变化纳入模型中,导致泛化能力变差;所以,本研究直接选择利用表述小样本泛化能力的交叉留一法均方根误差作为迭代的控制依据,均方根误差越小,模型效果越好,适应度越大。
控制均方根误差最小作为依据,需要一个模型对每一套特征子集的交叉留一法均方根误差进行拟合。该模型需要满足以下条件:①能对全部特征进行建模;②建模后无需对输入影响因素进行共线性检验、显著性检验;③模型具有很强的鲁棒性;④由于每次迭代需要随机进行2次交叉和2次变异,共计算4N次模型的交叉留一法均方根误差数值,所以需要模型本身具有很好的运行效率。条件①、②排除了需要进行各种检验的线性模型;条件④排除需要设置大量超参数的神经网络模型,如负反馈神经网络模型(BP),超参数是指机器学习在开始学习过程之前设置的参数,对于负反馈神经网络需要设置隐含层层数、单层神经元个数、学习率、动量因子等。随机森林则满足以上全部条件,随机森林的基本单元是决策树,本质是通过集成学习的思想将多棵回归决策树集成的一种算法。它具有以下两种优点:①能够处理具有高维特征的输入样本,而且不需要降维。②所需调节的超参数只限于决策树数量,与负反馈神经网络算法、支持向量机算法相比,需调节的超参数较少。所以,本研究选用随机森林回归模型交叉留一法均方根误差最小,作为遗传算法迭代的目标值。
对于小样本数据集采用交叉留一法验证其泛化能力并无争议;但随机森林算法自助抽样存在的随机变动性,导致即使在同一超参数和样本下每次交叉留一法结果均不相同,此问题在文献中并无相关研究。为了验证随机森林交叉留一法计算均方根误差的可行性,本研究在数据集中随机提取13个影响因素,并将决策树数目定为75,进行97 349次随机森林交叉留一法计算泛化均方根误差数值(见图3),计算结果整体概率呈现正态分布,其均值为19.643 6 t/hm2、方差为0.109 0、标准差为0.33 t/hm2;虽然每次训练泛化精度会有数值变动,但数值变动范围较小,取均值描述其交叉留一法泛化精度具有统计学意义。
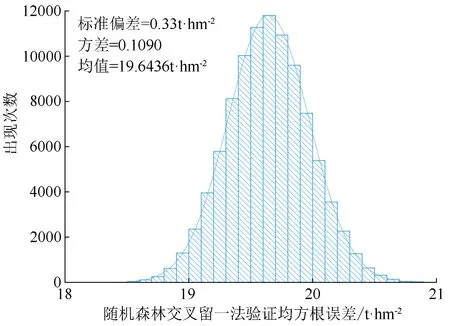
图3 97 349次计算随机森林模型交叉留一法均方根误差值概率分布及直方图
随机森林模型也需要超参数进行控制,与其他机器学习模型复杂的超参数相比,随机森林仅需要控制回归决策树的数目即可达到调节模型的目的。已有文献研究中,机器学习算法的超参数(如,负反馈神经网络模型的网络层数、神经元个数等)的确定,多数是通过依据反复试验的各种搜索方法(如,随机搜索、网格搜索)手动进行的[26]。手动对超参数进行调节,无法保证能发挥算法本身的最大潜力;而过于复杂的超参数会产生模型算法过于复杂,导致泛化能力变差,且运行时间过长;所以,机器学习算法超参数的调节,是一种优化。在利用遗传算法进行特征选择的同时,进行超参数的控制。
本研究先期测试中,输入整体特征集,分别对1~200个决策树时的随机森林模型进行拟合(见图4)。由图4可见:在决策树数量达到176时,随机森林拟合均方根误差曲线逐渐收敛于10.899 6 t/hm2;所以,本研究将决策树的范围设定为1~255的范围,此范围换算为二进制需要8位即E=8。在此基础上,增加决策树的数量对模型提升较小,且会明显增加模型运行时间。此时遗传算法求解的优化即为:在哪种特征子集及决策树数目时,能够得到泛化能力最好的估算森林地上生物量的随机森林模型。
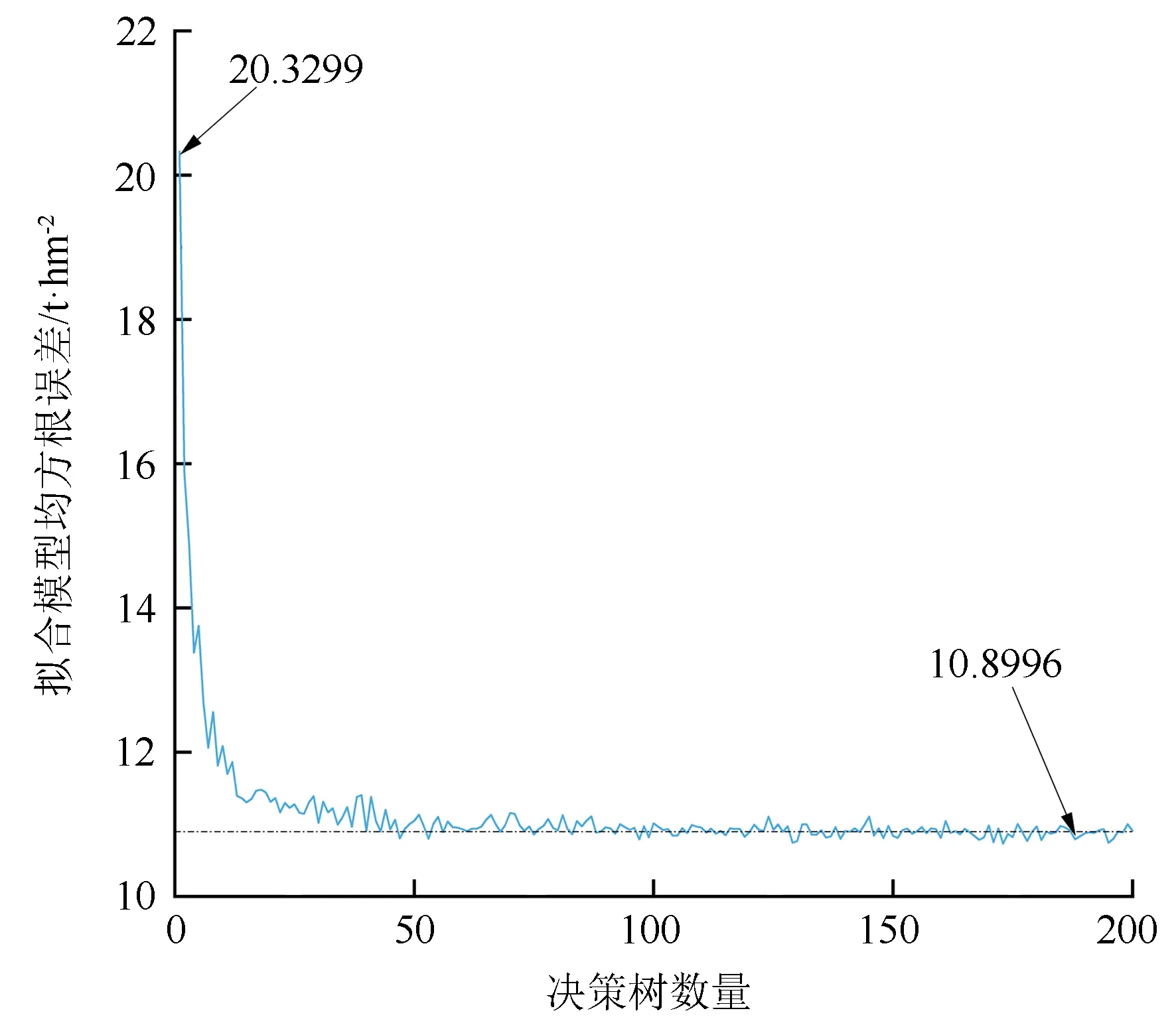
图4 随机森林模型拟合均方根误差与决策树数目关系曲线
将所有特征子集和决策树数量的组合,代入随机森林模型,计算交叉留一法均方根误差。由于随机森林本身存在波动性,所以取10次随机森林交叉留一法均方根误差的平均值作为当前组合的适应度;用随机森林交叉留一法所得均方根误差,计算动态自适应变异概率及交叉概率。目的是在当前个体较为优良时,采用较低交叉及变异概率保证最优个体保持稳定;在个体较差时,提高交叉及变异概率,以获取更优个体。
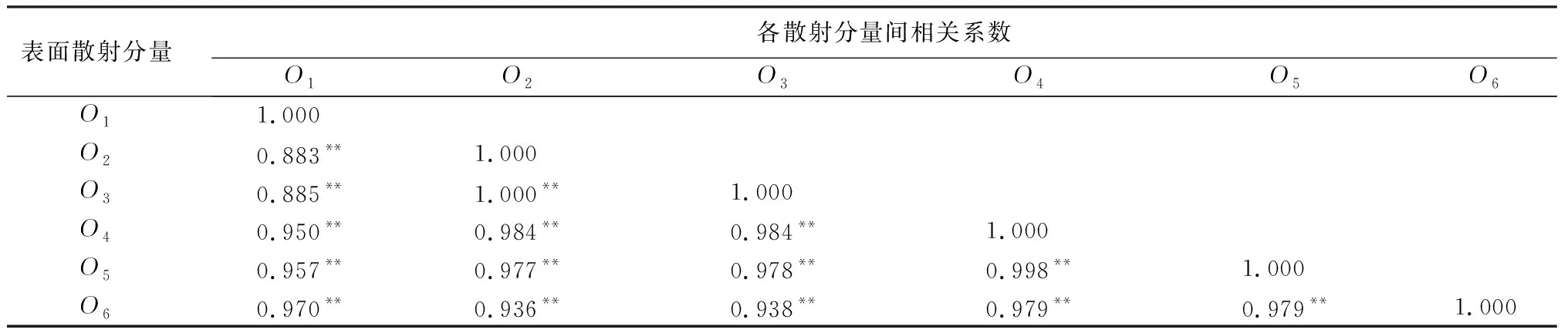
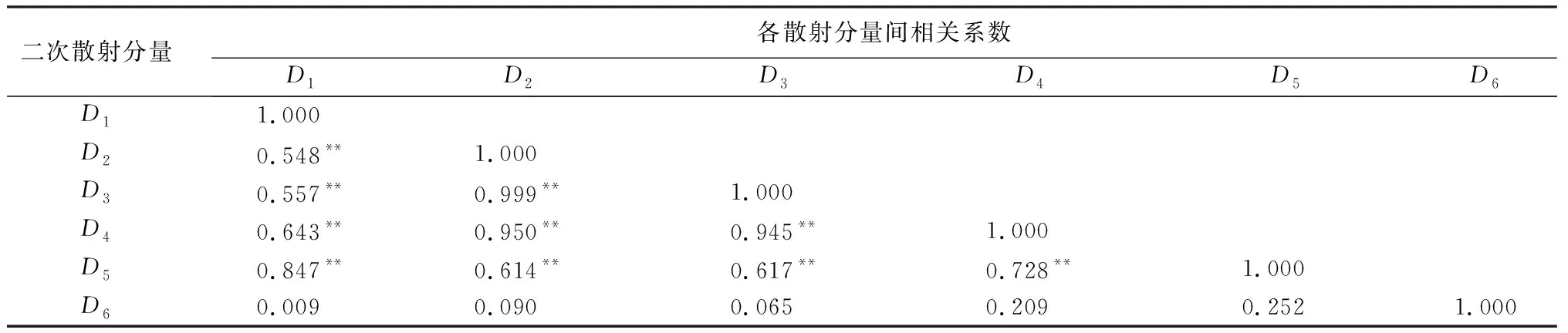
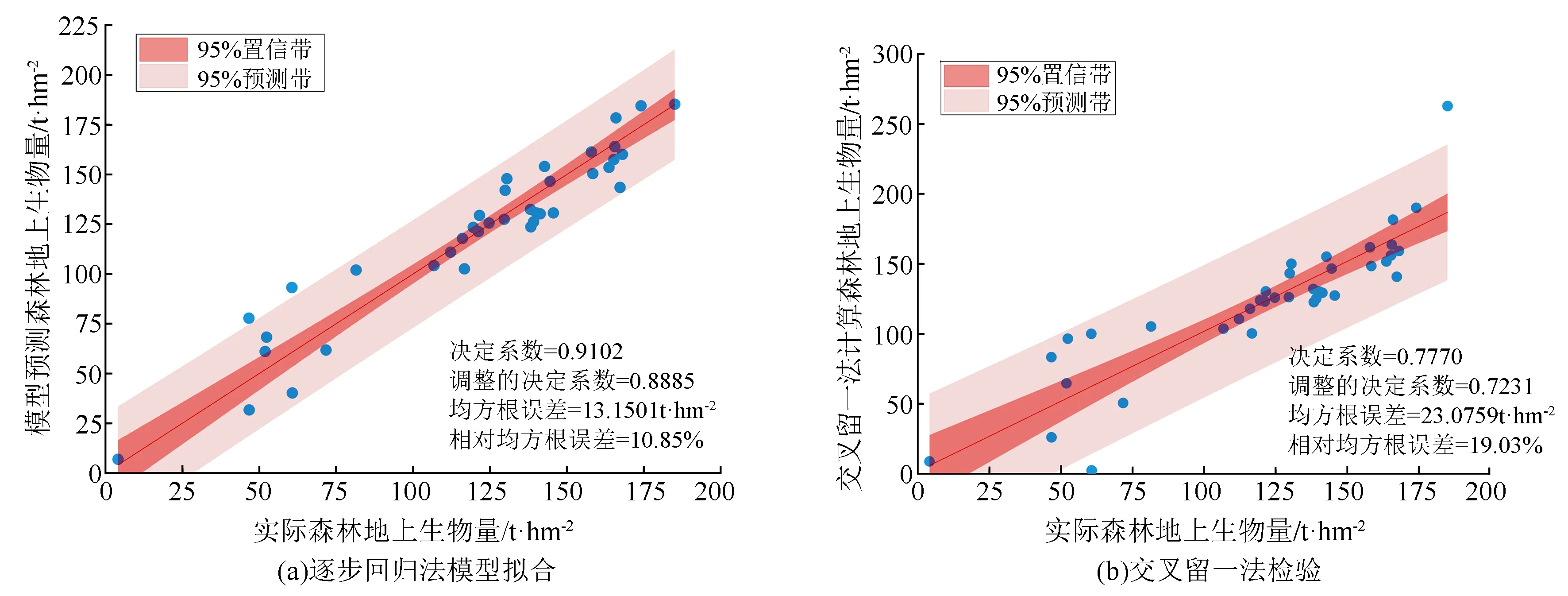
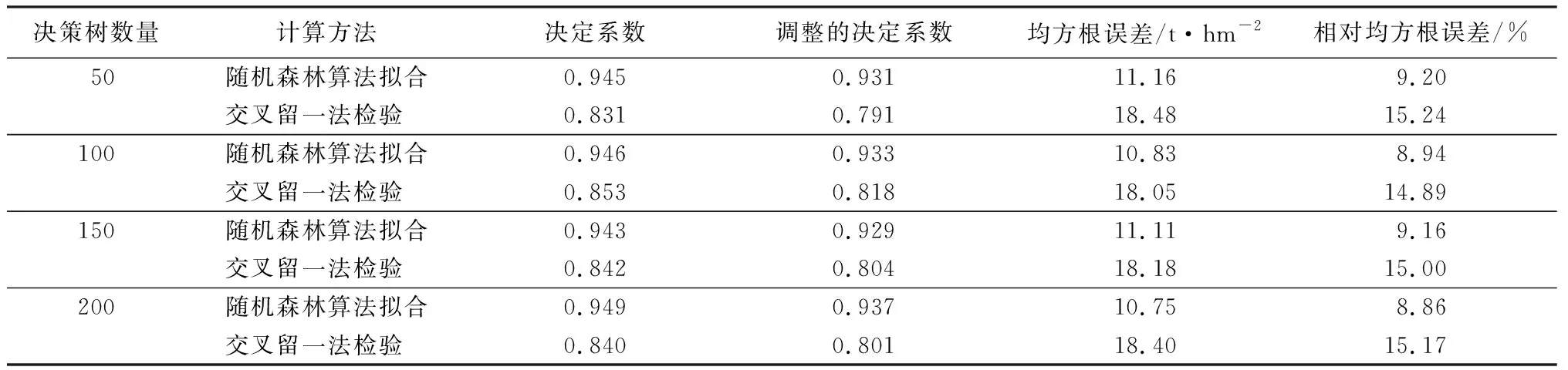
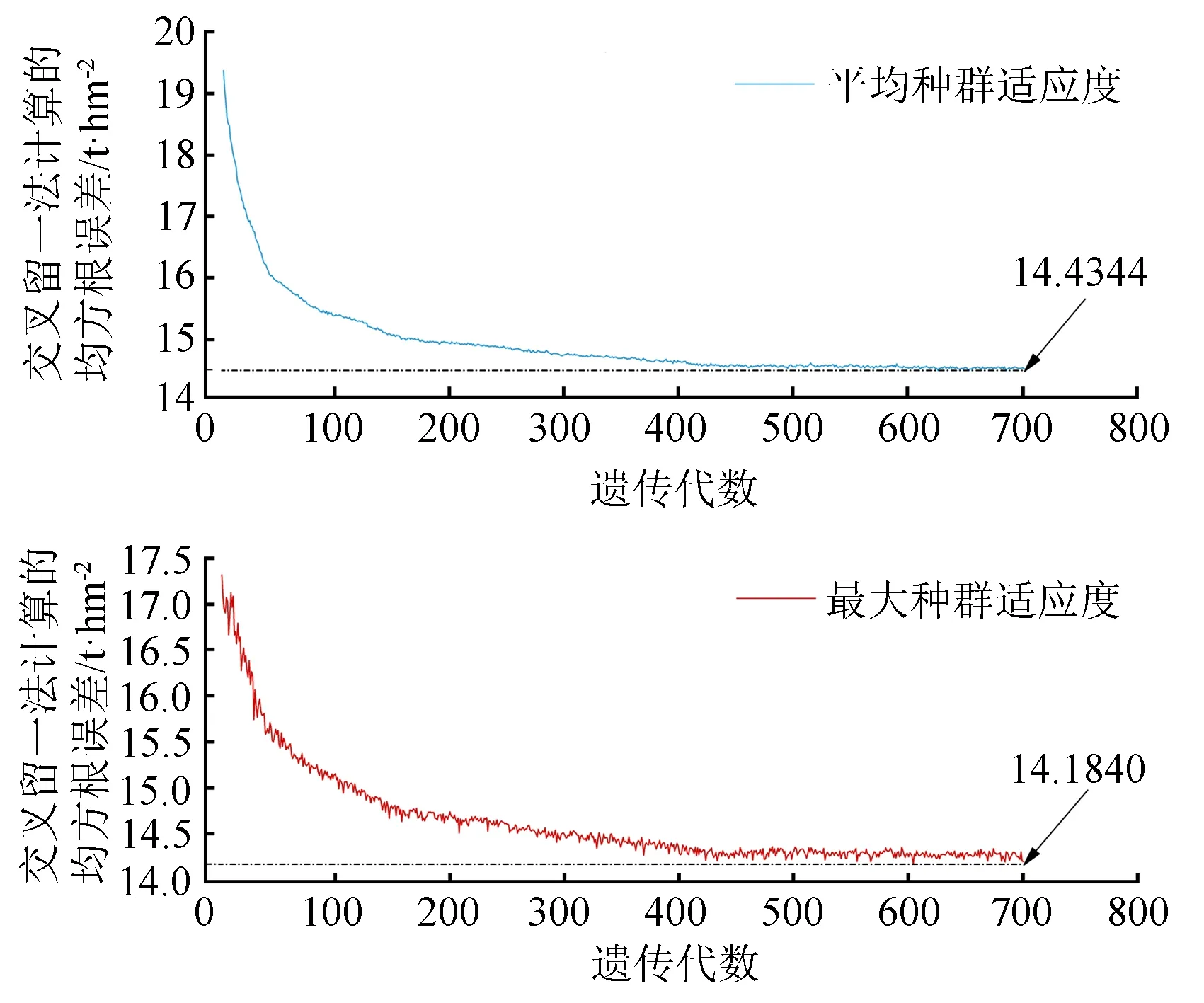
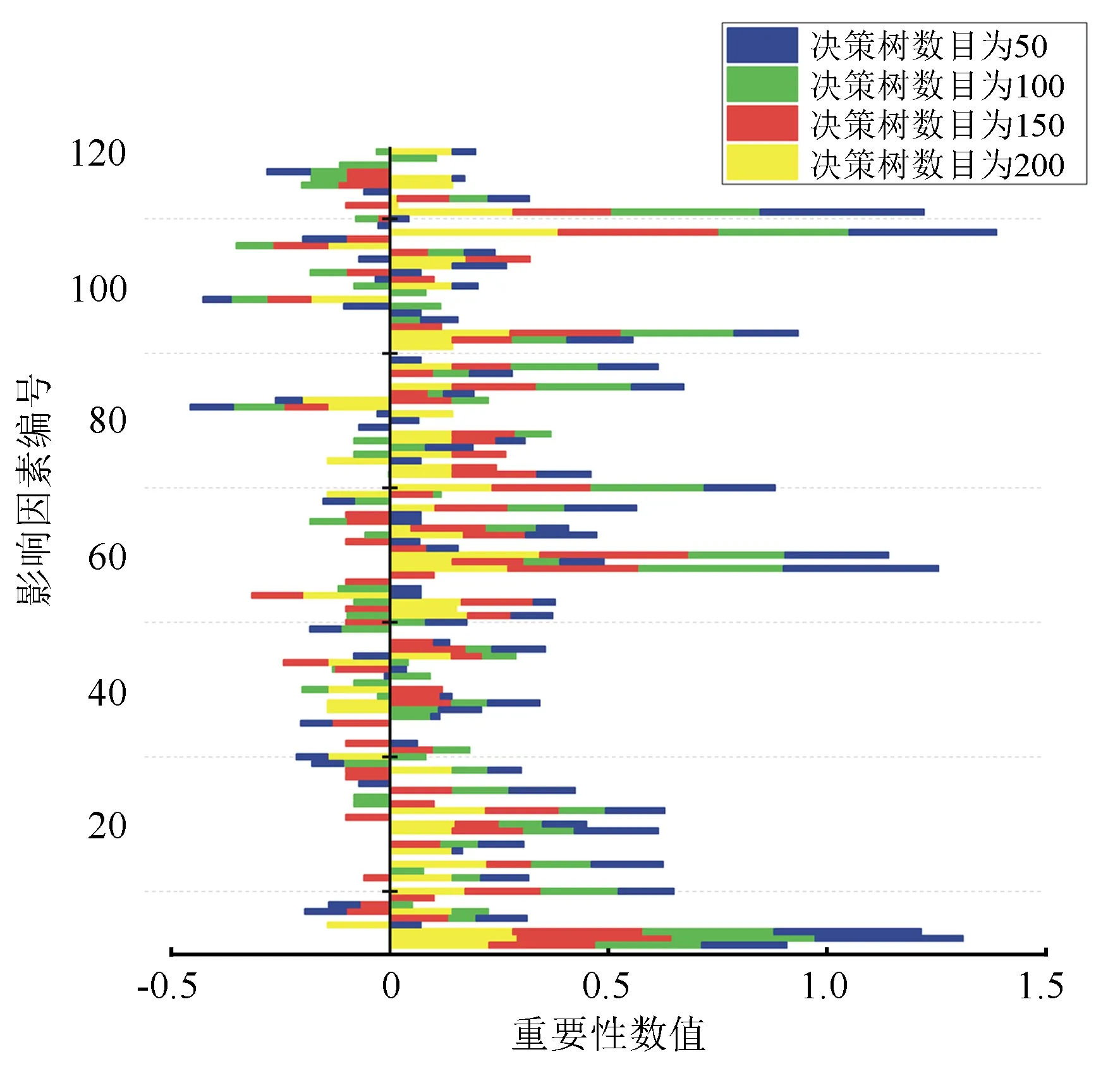
变异概率(PV,b):Fd 交叉概率(PV,j):Fd Fmax为最大适应度(即种群所有个体交叉留一法均方根误差最低值)、Favg为当前种群平均适应度(即种群所有个体交叉留一法均方根误差平均值)。当迭代至Fmax-Favg时,认为种群内所有个体交叉留一法均方根误差值趋于稳定,所选特征组合和决策树数目近似相同。此时,输出最优特征组合、决策树数目以及对应的随机森林交叉留一法均方根误差,迭代过程见图5。 RF为随机森林算法;AGA为自适应遗传算法;RF-AGA为随机森林与自适应遗传算法混合算法。图5 随机森林模型与自适应遗传算法的混合算法流程图 对提取的121个影响因素进行相关性分析,各影响因素之间相关性很高,且具有多重共线性。提取其中各极化方式体散射(见表1)、表面散射(见表2)、二次散射(见表3),各散射机制之间相关系数最高可达0.9以上。 表1 各极化分解方法体散射分量间的相关系数 表2 各极化分解方法表面散射分量间的相关系数 表3 各极化分解方法二次散射分量间的相关系数 利用全部121个影响因素、37个样本,分别输入随机森林模型与自适应遗传算法的混合算法、逐步回归法、随机森林回归算法,进行模型泛化精度对比。 逐步回归法:对逐步回归模型拟合与交叉留一法进行检验,模型通过显著性检验和多重共线性检验,拟合模型散点图与交叉留一法验证散点图见图6。 图6 逐步回归模型拟合、交叉留一法检验结果 最终线性模型为: BAG=252.139-1 823.265[DF3/(VF3+OF3)]-164.091An+ 0.454ψ1+1.594(GF2/VF2)+0.525α3-0.837τ- 0.434α2。 式中:BAG为森林地上生物量;DF3为弗里曼三分量分解二次散射分量;VF3为弗里曼三分量分解体散射分量;OF3为弗里曼三分量分解表面散射分量;An为依据特征值的“散射熵(H)-各向异性度(A)-平均散射角(α)”协同分解的各向异性值;ψ1为直推式支持向量机(TSVM)分解的相位参数;GF2为弗里曼二分量分解地面散射;VF2为弗里曼二分量分解体散射;α3为直推式支持向量机分解的第三散射角参数;τ为直推式支持向量机分解的目标最大特征状态椭圆率角;α2为直推式支持向量机分解的第二散射角参数。 随机森林回归算法:分别取决策树数量为50、100、150、200带入随机森林算法,拟合与泛化精度(见表4)。 表4 随机森林算法拟合与交叉留一法检验结果 随机森林模型与自适应遗传算法的混合算法(RF-LOOCV-AGA):经过700次迭代后遗传算法整体种群趋于稳定(见图7),平均种群适应度(Favg)-最大种群适应度(Fmax)=0.250 4 t/hm2。 图7 最大种群适应度及平均种群适应度随遗传次数的变化曲线 筛选出含有19个影响因素的特征子集:水平同向极化后向散射系数(σHH)、水平-垂直异向交叉极化后向散射系数(σHV)、垂直-水平异向交叉极化后向散射系数(σVH)、山口(Yamaguchi)三分量分解的体散射分量、安-杨(AnYang)三分量分解的二次散射分量、非负特征值(NNED)分解的体散射分量、“散射熵(H)-各向异性度(A)-平均散射角(α)”协同分解(H-A-α分解)的散射熵和各项异性度协同分量、依据特征向量的“散射熵(H)-各向异性度(A)-平均散射角(α)”协同分解的酉矩阵第二行二列相位因子(γ2)、依据特征向量的“散射熵(H)-各向异性度(A)-平均散射角(α)”协同分解的酉矩阵第三行三列相位因子(γ3)、弗里曼三分量分解二次散射分量(DF3)/[体散射分量(VF3)+表面散射分量(OF3)]、弗里曼三分量分解体散射分量(VF3)/[二次散射分量(DF3)+表面散射分量(OF3)]、弗里曼(Freeman)三分量分解表面散射分量(OF3)/[体散射分量(VF3)+二次散射分量(DF3)]、范西尔(VanZyl)三分量分解体散射分量/[二次散射分量+表面散射分量]、山口(Yamaguchi)三分量分解体散射分量/[二次散射分量+表面散射分量]、非负特征值分解(NNED)三分量分解体散射分量/[二次散射分量+表面散射分量]、非负特征值分解(NNED)表面散射分量/[体散射分量+二次散射分量]、依据特征值的“散射熵(H)-各向异性度(A)-平均散射角(α)”协同分解的单次反射特征值相对差异度、依据特征值的“散射熵(H)-各向异性度(A)-平均散射角(α)”协同分解的香农熵分量、T3矩阵的二行三列元素的实部以及T3矩阵的三行三列元素,决策树数量为255,计算出拟合精度与预测精度(见表5)。 表5 RF-LOOCV-AGA算法拟合与交叉留一法检验结果 由图8可见:利用随机森林对121个具有多重共线性的影响因素集进行重要性排序,分别取决策树数量为50、100、150、200;结果表明,在不同决策树数量时,重要性排序结果具有较大差异。如,第4影响因素(垂直同向极化(σVV)),当决策树数量为50、200时具有重要性,而决策树数量为100、150时重要性为0。同一影响因素在不同决策树数量时排序结果差异较大,随机森林特征选择算法在高维高共线性小样本数据中失效。 图8 决策树数量为50、100、150、200时各影响因素的重要性 利用随机森林算法袋外数据计算误差,对特征进行排序筛选,是常用的算法之一。在一定精度要求下进行特征的排序筛选,依靠两个方面,一是增大样本单元数,一是降低特征之间的共线性。但对于高维高共线性小样本数据,样本单元数有限,因此只能靠降低特征的共线性减小模型欠拟合或过拟合。高共线性不但使随机森林回归可能遇到的过拟合导致泛化能力差,也会导致特征选择排序的不准确性。在取极端共线性即两个影响因素完全相同时,即影响因素A等于影响因素B;随机森林的自抽样会随机保留其中一个影响因素作为重要影响因素,另一个影响因素重要性几乎为0。这是由于随机森林本身由有限决策树构成,决策树的构建属于局部贪婪算法导致的。决策树取影响因素A后性能提升显著,但再加入B时,由于A=B,所以决策树性能不会有任何变化;自抽样可能随机抽取A、B中任意一个,导致了随机森林随机保留其中一个影响因素作为极其重要影响因素,而另一个影响因素重要性几乎为0;而依据自适应遗传算法框架进行特征筛选,可以避免此问题。 本研究构建的随机森林模型与自适应遗传算法的混合算法(RF-LOOCV-AGA),作用、目的与逐步回归法最为类似。逐步回归法,利用传统的统计检验方法逐个将影响因素代入线性模型,进行显著性检验与多重共线性检验,将保留的影响因素集进行线性回归建模。随机森林模型与自适应遗传算法的混合算法从泛化能力考虑,求解当前数据集的最优泛化能力。高共线性影响模型精度的主要原因是:①高共线性影响因素的存在,导致模型过拟合泛化能力变差;②利用随机森林进行高共线性特征筛选时,可能导致影响因素重要性排序不唯一。随机森林模型与自适应遗传算法的混合算法,将自适应遗传算法的最优化能力、随机森林回归算法对高维小样本数据的强鲁棒性以及交叉留一法对模型泛化能力的强检验性充分结合。将高维高共线性小样本数据集特征筛选及参数回归,转换为:在何种影响因素子集及随机森林决策树数量时,能得到泛化能力最强的随机森林模型。 Campbell et al.[27]利用提出一种改进的随机森林算法对131个影响因素65个样本的数据集进行影响因素选择;该算法使用一个三阶段过程,该过程迭代地使用随机森林移除与结果几乎没有关系的影响因素、准确预测不需要的影响因素、最后的冗余影响因素,最后利用简约的预测影响因素集用于创建随机森林模型,预测森林地上生物量。与文献[27]的影响因素选择方法相比,本研究算法更具优势;因为本研究的研究对象是条件更为苛刻的具有高共线性高维度的小样本数据集,对于其他条件更为宽松的数据集同样适用。 提取大地2号全极化影像的后向散射系数与极化分解参数构建指数,以相关系数矩阵为基础,证明各极化分解影响因素之间有较高的多重共线性。 计算97 349次同一数据集随机森林交叉留一法均方根误差数值,结果表明整体概率呈现正态分布,均值为19.643 6 t/hm2、方差为0.109 0、标准差为0.33 t/hm2,证明交叉留一法可以用于随机森林模型;取若干次随机森林交叉留一法验证均方根误差的均值,可以表述随机森林模型的泛化能力。 分析在高共线性时决策树数量为50、100、150、200时随机森林特征排序,不同决策树数量时排序结果差异巨大,证明在高维高共线性小样本时随机森林特征排序法失效。 构建了随机森林模型与自适应遗传算法的混合算法(RF-LOOCV-AGA),适用于高维高共线性小样本林业数据的参数筛选和回归估计;并利用覆盖中国河北省承德市塞罕坝机械林场的大地2号全极化数据与37块地面实测样地,构建高维高共线性小样本数据集对随机森林模型与自适应遗传算法的混合算法进行应用测试,结果表明:与逐步回归法、随机森林算法相比,随机森林模型与自适应遗传算法的混合算法更适用于高维高共线性小样本数据回归估计与特征筛选。 此算法是首次提出并应用于高维高共线性小样本林业数据处理,在中国北方寒温带半干旱半湿润寒温性大陆季风气候的林区及大地2号全极化星载合成孔径雷达时取得了极好的效果,在其他传感器及林区的效果有待进一步验证。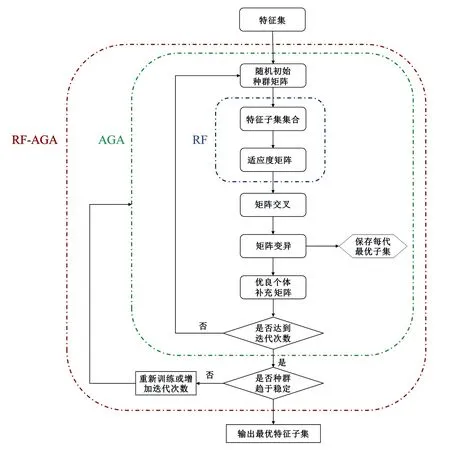
3 结果与分析
3.1 森林地上生物量估算中各影响因素的相关性

3.2 对森林地上生物量估算的3种算法精度比较

4 讨论
5 结论
