打磨教学细节构建精致课堂

2022-09-07江苏南通市北城小学226001周明新

小学教学参考 2022年17期

江苏南通市北城小学（226001）周明新

教学目标是判断教学是否有效的直接依据，教学目标的设置要有较强的针对性和目的性。教学活动应紧紧围绕教学目标展开，即使是在课堂收尾环节，也要尽力落实教学目标。要达到这一目标，教师备课时应精心构思，处理好每一个教学细节，避免脱离教学目标的随意提问和盲目活动。

细节一：“平移”，见微知著

在新授课中，教师若能对细节处理得当，抓住有价值的细节来大做文章，以小见大，那么就能够将静态的知识“盘活”，取得意想不到的效果。

例如，教学苏教版教材第六册“认识面积”时，教师可先让学生通过打手势演示平移和旋转，回顾旧知；接着呈现方格图（如图1，方格图中有一个绿点），让学生说明怎样将绿点向上平移10cm（学生口述，教师演示打点）；然后让学生画出绿点移动的轨迹（轨迹是一条线段，如图2）；最后让学生将线段向右平移20cm。

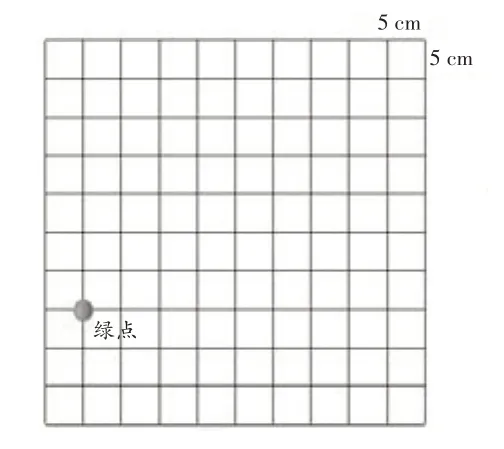
图1

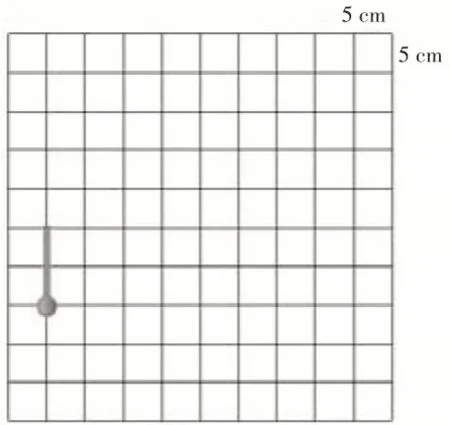
图2

事实上，线段的平移过程好似用油漆刷子刷油漆，从左至右“刷出”了一个长方形区域（如图3）。在直观演示后，教师让学生仿照前面的方法再“刷出”两个长方形。教师以这三个生成性图形作为素材，让学生观察对比它们的大小。学生动手操作、亲身体验，面积的意义不言自明。

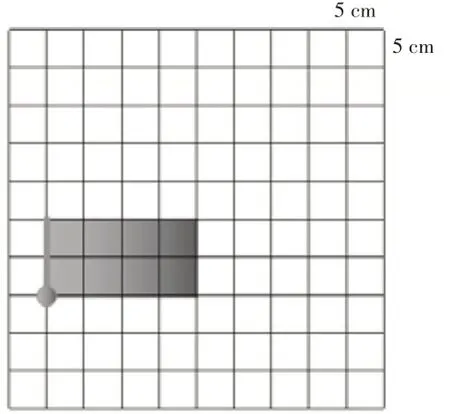
图3

上述教学中，通过在方格图中“移点成线”和“线扫为面”，将面积概念揭示得清清楚楚。点在方格图中移动，动态的移动过程具有连续性，既能引发学生的触觉认知，又可以引发学生的视觉感知。另外，面积单位本身就是由正方形来定义的，因此面积概念的形成就自带计量单位——方格格数。由点到线再到面的发展变化，也可以让学生有效区分周长和面积概念的不同。由此可见该教学环节细节处理的惊人威力。

细节二：“翻转”，出乎意料

对于苏教版教材第十一册“长方体和正方体的体积”的一道练习题“一个长方体紫檀木盒的容积是11.76dm³，包装工用它包装一个体积是7.2dm³的长方体砚台，能否完全装下？”，许多学生认为可以完全装下，而一些学生不能确定。此时教师不要急于告知学生答案，而是让学生先完成两道练习题。

题目1：一个紫檀木盒的内部尺寸为长28cm、宽20cm，容积为11.76dm³。包装工想用它装一块长25cm、宽16cm、高18cm的长方体砚台，能否完全装下？

题目2：一个紫檀木盒的内部尺寸为长28cm、宽20cm，容积为11.76dm³。包装工想用它装一块长25cm、宽16cm、高23cm的长方体砚台，能否完全装下？

为了方便分析问题，教师引导学生归纳整理题目信息：

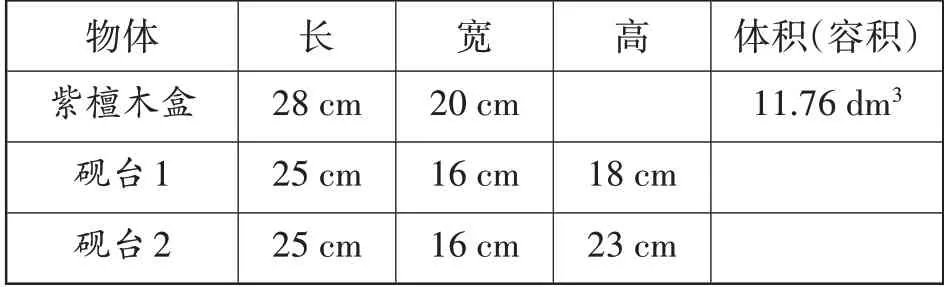
物体紫檀木盒砚台1砚台2长28cm 25cm 25cm宽20cm 16cm 16cm高18cm 23cm体积（容积）11.76dm³

生1：理论上，砚台1能够完全装入紫檀木盒中。因为砚台1的体积是25×16×18=7200（cm³）=7.2dm³，而7.2dm³<11.76dm³。仅看砚台1的体积小于紫檀木盒的容积，仍无法判断其是否可以装下。于是我又计算了紫檀木盒的高。11.76dm³=11760㎝³，11760÷（28×20）=21（cm），18cm<21cm。因为砚台的高小于紫檀木盒的高，所以能完全装下。

生2：砚台2不能完全装下。因为紫檀木盒的高是21cm，而砚台2的高是23cm，超高了，所以不能完全装下。

（按照教材的要求，教学已算圆满完成，但教师并未就此煞尾，而是继续拓展）

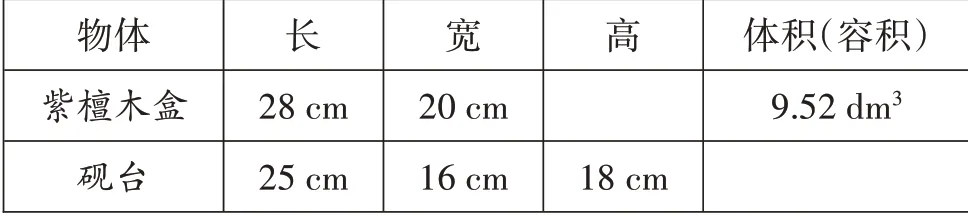
师（出示题目3）：一个紫檀木盒的内部尺寸为长28cm、宽20cm，容积为9.52dm³。包装工想用它装一块长25cm、宽16cm、高18cm的长方体砚台，能否完全装下？

为了方便分析题目的主要信息，教师指导学生对题干进行提炼归纳：

物体紫檀木盒砚台长28cm 25cm宽20cm 16cm高18cm体积（容积）9.52dm³

生3：我觉得不能完全装下。我是分两步考虑的。先进行体积对比，25×16×18=7200（cm³）=7.2dm³，7.2dm³<9.52dm³；再看长、宽、高是不是都符合尺寸规格，9.52dm³=9520㎝³，9520÷（28×20）=17（cm），17cm<18cm。因为砚台的高大于紫檀木盒的高，所以不能完全装下。

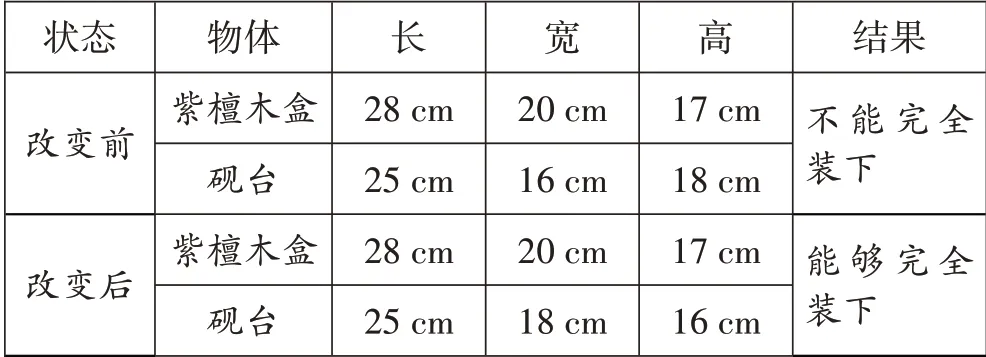
生4：我觉得能够完全装下。砚台的摆放角度不同，高度就会不同。换句话说，通过翻转，砚台的摆放角度改变了，其长、宽、高的位置就会互换。对此可以调整砚台的摆放角度，使其长、宽、高都小于紫檀木盒的长、宽、高，这样就能够完全装入紫檀木盒中了。

状态改变前改变后物体紫檀木盒砚台紫檀木盒砚台长28cm 25cm 28cm 25cm宽20cm 16cm 20cm 18cm高17cm 18cm 17cm 16cm结果不能完全装下能够完全装下

生5：这样表述比较乱，其实还有更简单的办法。把紫檀木盒与砚台的长、宽、高分别从大到小进行排列，再一一对照，如果紫檀木盒的长、宽、高大于砚台的长、宽、高，就表明砚台一定能够完全装入紫檀木盒，否则就装不下。

上述教学中，教师没有局限于习题本身，而是在不脱离教学目标的基础上，不断变式，深挖细节，不断推演出普遍情况，然后寻求这一类题目的最优解法和总结通用法则。

细节处理是否妥帖直接关乎解题正确与否，细节处理得越是精细，得出的方法和理论越是严谨可靠。若细节处理得粗糙，那么得出的解题方法不一定具有普遍性，一旦题型和情境有变，就无法变通，也就难以解决问题。

原题只给出了紫檀木盒和砚台的体积，问紫檀木盒是否能将砚台完全装下。这道题只告知了紫檀木盒和砚台的大致形状和体积大小，而没有告诉具体尺寸规格。面对这些不完善的条件，学生无法正确解答。

为了让学生得出正确、科学的解题方法，教师要不断丰富细节，将紫檀木盒的长、宽、高和砚台的长、宽、高分别“复原”，学生推理后就能总结出“要分别比较紫檀木盒和砚台的长、宽、高”的做法。当然，此时细节还可以继续丰富，那就是保持尺寸不变，调整摆放角度，看其是否能完全装下。正是因为教学细节处理到位，才能使学生总结出正确的解题方法：将紫檀木盒和砚台的长、宽、高分别按照从大到小的顺序排列，然后逐项比较。

细节三：“争论”，水到渠成

教师的“导”出现在何时最合适？无疑是学生出现学习困难时；无疑是学生初步得出结论又不敢确定时；无疑是学生小有成就就洋洋自得时；无疑是学生自以为是，听不进任何意见时。教师应处理好每个“导”的细节，积极引导学生交流讨论，帮助学生纠正错误，敦促学生自我反省。

例如，教学苏教版教材第八册“三位数乘两位数笔算乘法”时，在学生观察主题图，列出乘法算式850×15后，教师先让学生自己探究，再在组内交流讨论，然后展示学生的算法（如图1）。

图1

评讲时，教师先让学生观察分析各个算式，甄选出正确的算式；接着让学生查找错因，查不出错因的可以请外援，彻底查清后再重新做一遍；最后讲评两个正确的算式，比较哪个算法更优。

学生各执一词，分歧主要集中在0到底该不该参与计算。有的学生认为0不参与计算会简练些，有的学生认为0参与计算便于记录检查。对此，教师出示算式850×20，让学生计算，看谁算得又准又快。通过计算、讨论，学生得出结论：乘数末尾有0时，0最好不参加计算，只需在计算结束后清点积末尾的0的个数，注意不要遗漏。

学生自行钻研，辨别优劣，充分经历探究、遇阻、破解等过程，深刻领悟算理，牢固掌握算法。即便是在总结环节，教师也没有忽视细节，而是对学生进行及时疏导，使学生能够深刻领会笔算乘法的方法和策略，体现了教师的教学智慧。

细节四：“对比”，碰撞思维

课堂教学要想永葆活力，拓展延伸是必需的。在新课的提升环节中，教师可将细节放大，以开阔学生的视野，发散学生的思维。同时，教师还要善于发现学生思维的闪光点。

例如，教学“求平均数”时，教师出示例题：“手工（1）班有24人，平均每人剪窗花2朵；手工（2）班有26人，平均每人剪窗花3朵。问手工（1）班、手工（2）班平均每人剪窗花多少朵？”这一问题，主要有两种解法：①（24×2+26×3）÷（24+26）；②（2+3）÷2。解法①无疑是正确的。对于解法②，有许多学生持怀疑的态度，这些学生主要是受“移多补少”的思想影响。面对这种情况，教师可挖掘错误答案中的合理成分。

师：这里第一个2表示什么意义？

生1：2表示手工（1）班平均每人剪窗花的朵数。

师：也就是意味着手工（1）班每个同学剪窗花的朵数都可以视为2。那么3呢？

生2：3表示手工（2）班每个同学剪窗花的朵数，3也可以理解为手工（2）班26个同学每人均剪了3朵窗花。

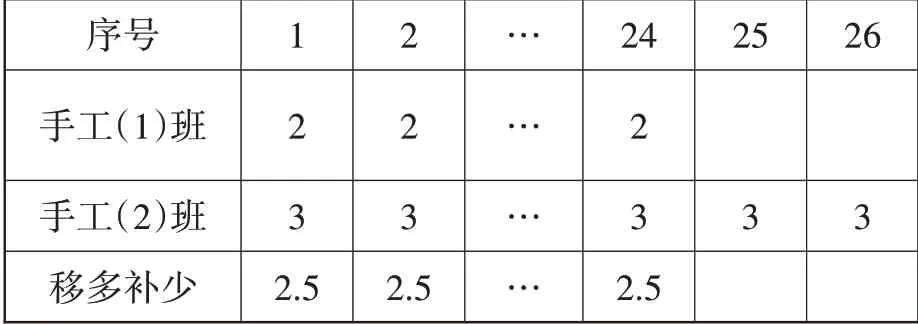
（教师引导学生列表理解）