基于问题驱动 促进思维发展

江苏海安市城南实验小学（226600）王 莉

在一次学习能力检测中，有一道题（如图1）：

图1

请在数轴上标出“8844”的大致位置。

这道题的正答率很低。笔者仔细分析了这道题，发现此题考查的是比较多位数的大小，这部分内容对学生来说并不难，假如此题换成“给8844、8500、8600、8700、8800、8900、9000排序”，正答率会高很多。那为什么换了一种考查题型，学生就束手无策了呢？

笔者认为原因有二：第一，不少学生缺乏自主思考的能力，在教材中出现过如图2这样的题目，在方框里填数，这题对学生来说没有难度，但是上题并没有让学生将数轴上缺少的数补上，正因为少了这个跳板，学生解题时不知该从何处着手，导致错误百出；第二，平时的学习中，教师和学生侧重训练比较多位数的大小的方法和技能，忽视了对数的大小的感悟。

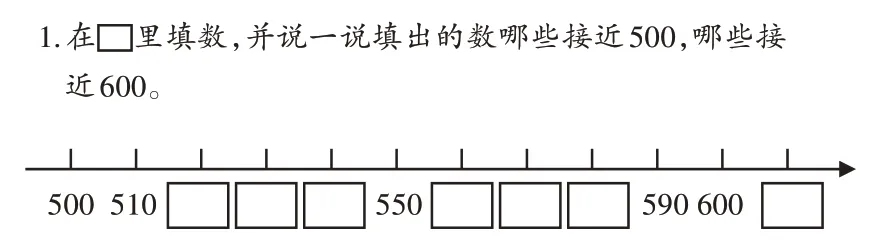
图2

通过数学学习培养学生的思维，是数学教育的重要目标。虽然教师都知道这一点，并且一直在为此努力，但是像上述问题一样，学生不会思考的现象不在少数，且低年级学生尤其明显。原因当然有学生年龄特征的影响、智力方面的差异，试着摒弃这些客观原因，反思课堂，是否有不足之处呢？

笔者认为下面几种情况值得关注。

1.注重形式，忽视本质。自课程改革以来，很多新的学习方式走进课堂，如小组合作、动手操作、交流分享等方式让学生的主体地位得到充分发挥，极大地调动了学生的学习积极性。同时，笔者也发现，有时在课上学生忙得不亦乐乎，很少有静下来思考的时间，课堂热闹了，但课堂学习效果却不理想。究其原因，是教师过多关注课堂形式，忽视数学本质，没有在关键环节上让学生停一停、静一静、想一想。

2.注重知识，忽视能力。教师为了追求高效课堂，在教学过程中习惯“小步子前进”，用细化的问题引领着学生一步一步探索问题的答案。这样的课堂，教师容易驾驭，课堂教学效果好，知识技能训练扎实，但忽视了学生思维能力的培养。最明显的表现是学生在考试中会做练过的题，不会做没有练过的题。久而久之，学生会形成思维定式，只做熟悉的题，不做陌生的题。

3.注重解题，忽视反思。长期以来，很多教师把解题当作学生学习的目标，认为课堂学习就是为了会做题，因此课堂缺少比较、反思和总结的环节。在这样的课堂中，学生获得的是一个个零散的知识点，没有构建知识网络，时间一长，这些知识便被遗忘，这是很多学生觉得数学难的一个重要原因。

低年级学生的年龄小，自主思考的意识和能力都比较弱，该如何引领他们思考呢？笔者认为在教学时应把握时机，通过合适的问题驱动学生思考，这是发展学生数学思维的重要途径。

一、设计前置性问题，培养思维的意识

著名的数学教育家托利亚尔指出：数学思维是数学的内在精髓。如果学数学仅仅满足于会计算，掌握一些必要的公式、定理，而不思考“为什么这样算？有没有更有效的方法？这些公式和定理是如何发现的？”这些问题，那么这样的学习是盲目的，最终获得的也只是一些程式化的内容，对于解决新问题没有任何帮助。教师可以设计一些前置性问题，让学生在动手之前先动脑，可以有效地培养学生的思维意识。

学生学习了“两、三位数加减法”之后，教师出示以下练习题：

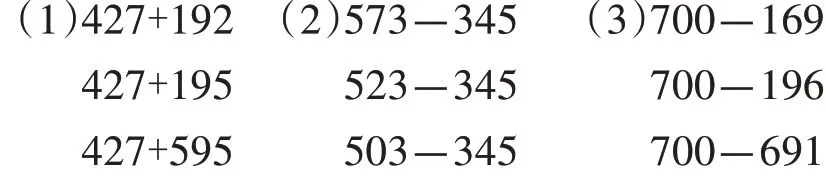
如果仅仅让学生计算这些题，再核对答案，就只是巩固了多位数加减法的计算方法，学生的思维没有得到发展。

因此，教师出示题目之后，并没有让学生直接计算，而是先让学生观察这三组算式，看看有什么发现。学生发现：第一组算式的第一个加数都相同，第二个加数越来越大；第二组算式的减数相同，被减数越来越小；第三组算式的被减数相同，减数越来越大。

接着，教师又让学生猜第一组算式的计算结果会是怎样的，并说说自己的想法。学生想到：第一组三个算式的得数会越来越大，因为第一个加数都相同，第二个加数越来越大，得数也越来越大；第二组算式的减数相同，被减数越来越小，得数也越来越小；第三组算式的被减数相同，减数越来越小，得数也越来越大。

这样既达到了让学生巩固计算方法、提高计算技能的目的，又教会学生用数学的眼光看问题，用数学的思维想问题。

二、设计质疑性问题，调整思维的角度

学生的思维发展不是一蹴而就的，是要经历一个长期的过程。当学生在思考问题的过程中陷入瓶颈时，教师可以把握时机，提出质疑性问题，引导学生及时调整思维的角度，进而解决问题。

如在教学“多位数的加减法”时有一道题：

小明和小红同时开始看一本同样的故事书，几天后，小红看了120页，小明看了85页。（ ）剩下的页数多，多（ ）页。

A.小红 B.小明 C.120+85 D.120－85E.无法计算

第一个问题学生基本都明白：同一本书，看得多就剩得少，看得少就剩得多。但是在解决第二个问题时，很多学生认为不知道故事书的总页数，不能求出他们各自剩下的页数，因此第二个问题无法求出。此时，教师问：“真的求不出来吗？”一些本来就有点想法的学生经教师这么一点拨，马上大胆地提出可以用“120-85”来算。教师没有表态，而是继续问：“不是要比剩下的页数吗？120和85是已看的页数，为什么用已看的页数相减呢？”有学生通过画图发现：小明比小红少看的页数就是小明比小红多剩的页数。由此，复杂的数量关系得到梳理，学生的思维也迈上了一个台阶。

除了上述情况，当学生对问题的认识不够全面时，教师也可以通过质疑性问题把学生的思维引向深处，让学生在追问中认识问题的本质，发展思维能力。比如，学生在学习了“得数是10的加法”以及“10减几”之后，笔者设计了一道“射击比赛”题（如图3）。

图3

师：小丽两次射击最多能得几分？最少能得几分呢？

生1：我觉得最多能得9分，最少能得5分。

师：说说看，你是怎么想的？

生1：最多的话，会打中4分和5分那环，4+5=9（分）；最少的话，会打中2分和3分那环，2+3=5（分）。因此最多能得9分，最少能得5分。

师：同意生1的意见的请举手！

（大部分学生举手，少部分学生犹豫）

师：两次射击的得分一定不同吗？

生2：我觉得最多可以得10分。

师：说说你的想法。

生2：如果运气好的话，小丽可能两次都打中5分那环，这样就能得10分了。

师：你们觉得有可能吗？

生3：有可能！

师（动画演示）：第一次射击打中了最里面一环，得了5分，第二次射击会不会还能打中最里面一环？

生4：可能会。

师：同理，最少能得几分呢？

生5：两次射击都打中最外面一环，两次最少得2+2=4（分）。

师：现在同意最多能得10分，最少能得4分的举手！

（全班学生一致举手）

师：为什么跟你们刚开始的想法不一样了？

生6：没有想到两次都打中同一环。

师：看来，我们遇到问题时，还要换个角度多想一想，看看是不是还有其他可能。

上述教学过程中，学生刚开始的思考角度是两次得分不同的情况，教师的质疑性问题引导学生意识到还存在两次得分相同的情况。小学生的年龄小，知识和经验不足，认识有局限性，通过质疑性问题可以帮助他们调整思维的角度，让他们的认识更全面。

三、设计变式性问题，拓宽思维的广度

郑毓信教授指出：数学基本技能的教学，不应求全，而应求变。在变化的数学问题中，学生更容易通过比较把握问题的本质，拓宽思维的广度。变式可以是纵向变式，即引领学生向更复杂的知识领域思考；也可以是横向变式，引领学生思考与所学知识相关的问题，通过比较发现它们的异同，了解它们的联系和区别。

例如，一道练习题（如图4）：

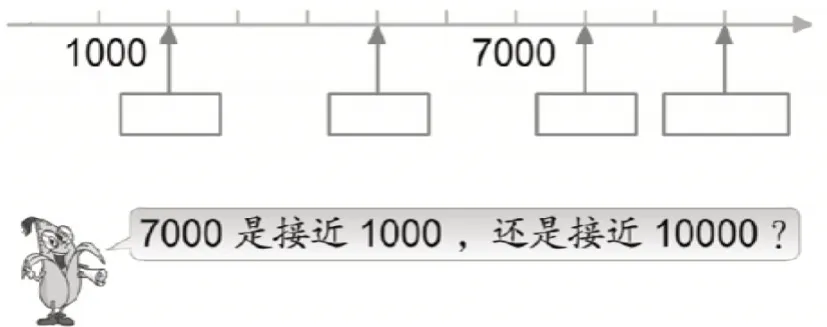
图4

在学生完成练习之后，教师追问“你是怎样想的”，将学生的思维引向深处。学生发现数轴右边的数比左边的大，每一格表示1000。再通过问题“你觉得图5的这个点所在的位置，用哪个数表示比较合适？”引导学生估计非整千数的位置。在此基础上，教师还可以进一步纵向延伸，改动数轴（如图6）。

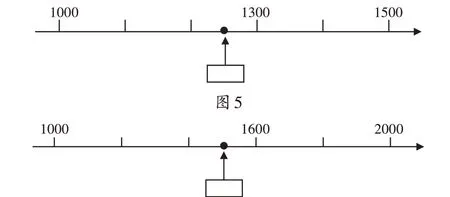
图6

图4的数轴中1格表示1000，图4的数轴中1格表示100，图6的数轴中1格表示200，难度逐步提升。这些问题仅靠浅层次的模仿是无法顺利解决的，需要学生深入思考，发现数轴上的已知数发生了变化，每一格所表示的数就随之发生变化，同一个位置上所表示的数也发生了变化。经历了这样的思考过程，学生的思维自然获得了发展。

四、设计总结性问题，挖掘思维的深度

总结性问题也称为后置性问题，即在解决问题之后，引导学生对解决问题的过程进行反思总结，以便更好地梳理知识的脉络，掌握解决问题的方法，形成知识结构和方法结构。

例如，教学“万以内的数”时，有这样一道题：

用4颗算珠在算盘上可以表示不同的三位数，其中最大的是多少？最小的是多少？

学生先尝试用4颗算珠表示出三位数，找到最大的三位数和最小的三位数后，教师再引导学生用4颗算珠表示不同的四位数以及用6颗算珠表示不同的四位数，最后提问：“谁能总结一下怎样才能很快地利用算珠表示符合要求的多位数呢？”学生发现：要表示最大的数，就要尽量多放算珠在高位，先放上珠，再放下珠，因为1颗上珠表示5，1颗下珠表示1，如果最高位放不下，再依次放到第二位、第三位，但是在每一位上都是先放上珠，再放下珠；要表示最小的数，最高位只能放1颗下珠，剩下的算珠从最低位（个位）开始放，但要注意都是先放下珠，再放上珠。

上述教学中，教师通过总结性问题引导学生回顾解决问题的过程，归纳概括用算珠表示数的方法，学生的思维由模糊走向清晰。

综上所述，教师在课堂上可以利用前置性问题培养思维的意识，利用质疑性问题调整思维的角度，利用变式性问题拓宽思维的广度，利用总结性问题挖掘思维的深度。在课堂实施的过程中，对何时提出问题、提出什么问题可以发展学生思维，没有严格划分，这需要教师把握时机，设计出切实有效的问题，让学生获得启发，促进学生数学思维的有效提升。当然，利用问题发展学生的数学思维只是一种途径。促进学生的思维发展还有哪些路径，需要广大教师继续研究和思考，所幸我们一直在路上。