以表达促理解，培养学生的计算能力——“两位数加两位数的口算”的教学实践与思考

江苏南京市科睿小学（210019）陈恩慧

【教学内容】

苏教版教材二年级下册第59页的例1和第60页的“想想做做”第1-5题。

【教学背景】

“两位数加两位数的口算”是在学生掌握了“100以内两位数加减一位数、整十数”“两位数加减两位数笔算”基础上进行的。由于学生已经有了丰富的笔算经验，所以在学习口算方法时，容易受到笔算方法的干扰。如果教师在新授课环节直接出示例题进行教学，绝大多数学生都会选择笔算的方式，而本课要求学生通过掌握口算来进一步完善计算能力。基于此，课中教师应注重引导学生理解口算的算理，经历口算算法的探究过程，在表达与交流中理解和掌握口算技能，提高计算正确率。

【教学过程】

一、基于条件，精准提问

【片段1】课间活动时，很多小朋友喜欢跳绳，图1是3个小朋友跳绳的情况。

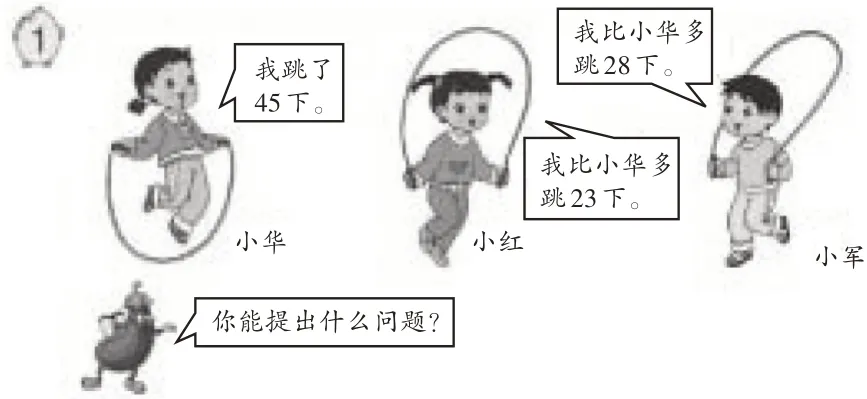
图1

师：你能根据图中的条件提一个问题吗？

生1：小红和小军一共跳了多少下？

生2：3人一共跳了多少下？

……

【思考】课堂开始部分，学生根据条件独立提出问题，出现了各种状况。有的学生会提出“小红和小军一共跳了多少下”“3人一共跳了多少下”等问题，虽然问题没错，但是涉及多步计算。于是笔者将问题改为“你能提一个一步计算的问题吗”，或“你能从中任选两个条件提一个一步计算的问题吗”，这样才能使学生明确地提出对应的问题。教师的精准表达可以促使学生更有针对性的思考，从而提出更合适的问题。同时学生在这一环节不必将大量时间浪费在提问上，而把时间与思考放在探究算法与算理上。

二、算法多样，自主表达

【片段2】在学生提出“小红跳了多少下”和“小军跳了多少下”的问题之后，笔者顺势展开教学。

师：我们先来算一算小红跳了多少下。

师：你想怎么口算“45+23=”？

（如果学生先算个位，教师可根据学生的回答在黑板上贴出对应的过程）

师：你是先算45加3，然后再加20。

（如果学生先算十位，教师可根据学生的回答在黑板上贴出对应的过程）

师：你是先算45加20，然后再加3。

师：还有不同的口算方法吗？把你的想法写在学习单上的方框里。（出示图2）

图2

师：现在请同学们以四人为小组交流，先讨论不同的口算方法，再请方法最多的小组来汇报。

生1：我是这样算的，45+20=65，65+3=68，先算几十几加几十，再加几。

生2：我是这样算的，40+20=60，5+3=8，60+8=68，先算几十加几十，再算几加几，最后把两部分合起来。

生3：我是这样算的，45+3=48，48+20=68，先算几十几加几，再加几十。

生4：我是这样算的，5+3=8，40+20=60，8+60=68，先算几加几，再算几十加几十，最后把两部分合起来。

师：这四种口算方法，结果都等于68。恭喜你们组算对了，而且找到的方法最多！

师：刚才在口算“45+23”时，其实同学们都想到了同一种方法——拆数，这样就把我们今天要学的新知识转化成学过的两位数加整十数、两位数加一位数的知识。

【思考】每位学生都有自己的计算方法，无论是笔算的思想还是口算的思想，只要思路正确，都应给予肯定。在有限的40分钟内，既要让学生表达得清楚，又要使学生理解得深入。于是，在出示“45+23”这道算式后，笔者先请一位学生说说他的口算方法，再请另一位学生来说说他的口算方法，两种方法叠加以达到强化的效果。相反，如果第一位学生说的是笔算方法，那就直接进入小组讨论环节，并提出“先讨论不同的口算方法，再请方法最多的小组来汇报”的要求，以达到鼓励学生思考不同口算方法的目的。课堂是属于每一位学生的，因此在探索环节，教师应该充分放手让学生自己去探索、去讨论、去发现，尽情表达数学，促进其对数学知识的深度理解。

三、尝试分类，抽象算法

【片段3】笔者出示图3。

图3

师：你能给这些算法分分类吗？小组商量一下。

生1：算法1和算法3分为一类，算法2和算法4分为一类。

师：为什么这样分呢？

生1：因为算法1和算法3都是两步计算，而算法2和算法4都是三步计算。

师：其他同学有不一样的分法吗？

生2：算法1和算法2分为一类，算法3和算法4分为一类。因为算法1和算法2都是先加几十，再加几；算法3和算法4都是先加几，再加几十。

师：同学们说得好！我们先看算法3和算法4。算法3是先算45加几，再加几十；算法4是先算几加几，再算几十加几十，最后把两部分合起来。这都是我们之前学的笔算算法，而我们今天要学的是口算算法，口算两位数加两位数时，一般从高位算起，就像算法1和算法2。算法1是先算45加20（描红“4”和“2”），再加3；算法2是先算40加20（描红“4”和“2”），再算5加3，最后把两部分合起来。

师：请同学们再仔细地看一看算法1和算法2，哪一种更简便呢？

【思考】从本节课的教学目标来看，笔者希望学生的分类是：算法1和算法2分为一类，因为它们都是先加几十，即先算高位；算法3和算法4分为一类，因为它们都是先加几，即先算低位。尽管在汇报不同算法时，笔者已经强调了口算的算法是“先加几十，再加几”，但在分类过程中，学生更倾向于直观感受。基于二年级学生思维直观性强这一特点，笔者调整了板书布局（如图4），先直观地引导学生将算法1和算法2分为一类，再通过解释这样分的道理，让学生逐步感受“先加几十，再加几”的深层含义。

图4

四、对比分析，沟通联系

【片段4】

师：同学们已经口算出小红和小军各跳了多少下，真棒！仔细观察“45+23”和“45+28”的口算过程（如图5），有什么相同点和不同点，同桌互相说一说。

图5

生1：“45+23”和“45+28”都可以先算45加20，再加几。

生2：“45+23”和“45+28”都可以先算40加20，再算几加几，最后把两部分合起来。

师：都是45加二十几，怎么一个得数是六十几，一个得数是七十几？（描红“6”和“7”）

生3：因为“45+23”的个位上是5加3，没有满十，不用进位，所以得数是六十几；而“45+28”的个位上是5加8，满十要进位，所以得数是七十几。

【思考】在对比中分析异同，并表达异同，学生在不知不觉中沟通了联系，总结出“先加几十，再加几”这一口算算法。课堂上，学生的每一句发言其实都是最真实的数学表达，学生将知识进行了梳理与加工后，用自己的语言表达出来，这也反映了学生的理解情况以及对课堂学习的真实掌握情况。多给学生机会去表达，让他们完善自己的想法，可以促进他们更好地掌握口算方法、理解算理，从而形成计算技能。

【案例反思】

本课的设计紧扣重难点，在探索两位数加两位数的口算方法过程中，教师给学生提供了多种表达机会，活跃了学生的思维，巩固了口算方法。学生在表达的过程中既厘清了自己的思路，也学习了别人的观点。表达激发了学生的学习兴趣，打开了数学思维，促进了计算理解，从而达到落实深度学习的目的。

一、创设表达机会，让学生化身课堂小主人

低年级学生的认知发展处于具体运算阶段，他们以形象思维为主，主要通过对实物的感知和操作获得基本的数学知识和能力。基于低年级学生的思维特点，教师可在课堂上多为学生创设表达的活动，如教学片段3，让学生对自己的分类标准畅所欲言。看似简单的任务，却需要学生仔细思量，取得了有的放矢的效果。当教师给学生充分的时间和空间去思索、去交流、去表达时，学生化身为课堂的小主人，在表达中推进思考，促进理解。

二、开放表达空间，激发学生自主学习兴趣

教师在创设表达机会后，还需要开放表达空间，使学生自由表达，以此来激发学生的学习兴趣。

“45+23=”虽是一道普通的算式，却有着多种多样的算法，每一种算法背后都蕴藏着学生自己的理解和数学思想。学生在倾听了别人的方法后又收获了新方法，同时也促进了自己的思考，使表达更完整。当开放表达空间后，计算课不再只是单调枯燥的计算，而是学生的自主思考、自主研究过程，并在多种表达中碰撞出智慧的火花。

在比较环节给学生提供开放的表达空间，不同学生表达出的“异”与“同”也不一样。课堂属于每一位学生，当学生发自内心地想要去解决一个问题时，就会再进一步思考，再进一步表达，在表达中产生兴趣，而兴趣会带着学生走进“计算的世界”，进行深度学习。

三、营造表达氛围，带领学生深度学好计算

课堂的理想状态是学生愿意表达、积极表达、享受表达。当表达成为一种习惯，学生沉浸在表达的氛围中时，计算将不再枯燥，也不再浮于表面。案例中，当学生已经口算出小红和小军各跳了多少下的问题后，笔者继续抛出问题“有什么相同点和不同点”给学生持续营造一种表达氛围，学生基于自己的理解勇敢表达想法，有利于学生明确不同方法间的联系，从而掌握口算方法，理解口算算理，深度学习计算。

课堂中，教师应鼓励学生积极思考，将观点表达出来，将思考分享出来。如此，学生便可在理解算理的基础上掌握算法，在掌握算法的基础上深化理解，在表达的过程中丰富感性认识，并逐步由感性认识上升到理性认识，促使知识内化。每一次的表达都在传递着每一次的理解，学生在一次次表达与理解中，使知识体系呈螺旋式上升，从而更精准、更有深度地学习计算！