数学建模：从“结构”走向“建构”——提升小学生问题解决能力的教学策略

浙江杭州钱塘新区临江新城实验学校（310020）雷兴荣

《义务教育数学课程标准（2011年版）》指出：在“问题解决”的教学中，不仅要关注数学问题解决的结果，更要关注学生在解决数学问题中思维的过程。因此，教师要引导学生在实际情境中从数学的视角发现和提出问题、分析问题、建立模型，增强学生解决实际问题的意识和能力。

一、建模困境：小学数学问题解决教学的现状审视

1.缺少建模，思维散乱

一些教师只注重问题解决方法的训练，缺乏对学生分析、加工、整合信息能力的培养，没能引导学生总结问题解决的策略，形成系统的问题解决的模型。

例如，用车运煤，现有载重2吨和3吨的两辆车，要求每辆车每次都要装满，正好可以运完8吨煤，如何安排最合理呢？

某教师首先让学生自主探究，完成表格的填写；然后呈现表格（如表1），选择恰好运完的情况，列出算式4×2+0×3=8（吨）或1×2+2×3=8（吨）；最后给出其他练习让学生训练。

表1

这位教师重视学生解题能力的培养，但过于偏重解题结果，缺乏问题解决模型的构建。

2.错误建模，不善迁移

数学建模应该是基于学生的学习起点、思维方式和问题本质而形成的问题解决策略。但是一些教师在问题解决教学时给学生建立的所谓“模型”并没有基于问题解决的本质特征。

例如，人教版教材一年级上册问题解决（如图1）教学中，关于加法模型、减法模型，一些教师教学时都是告知学生：“见到‘一共’，就圈上，列加法算式解答；见到‘剩下’，就列减法算式解答。在图形列式中，‘？’在下面的做加法，‘？’在上面的做减法。”

图1

这样的教学没有真正借助情境去帮助学生理解加法和减法运算的意义。

3.固化模型，机械运用

在分数、百分数解决问题教学中，为了增强学生解决问题的意识和能力，一些教师首先将问题分成知道单位“1”和不知道单位“1”，根据两种情况，分别建立模型：若知道单位“1”，就用乘法（算术法），用单位“1”的量×对应分率；若不知道“单位1”，就用除法（算术法），用已知量÷对应分率。这样的教学加上强化练习，看似提升了学生的问题解决能力，但学生的思维也固化了。

二、建模途径：提升小学生问题解决能力的建模策略

1.正确建模——引发思考，抽象本质

（1）精选素材，激发建模兴趣

合理的素材可以让抽象的知识与学生的经验建立联系，引导学生通过联想、类比等多种思维方式学习。因此，教师要认真选择数学素材，培养学生数学建模的兴趣。

【案例1】“统计图”的教学

师：育才小学小导游社团的孩子对西湖接待的游客进行了数据统计。

师（出示无数据的统计图，图略）：你认为哪张图表示的接待游客多呢？

师（在图中补充数据，如图2-1）：现在你知道了吗？

图2-1

生1：两张图表示的都一样多。

师：曲线明明不一样，怎么会一样多呢？

生2：因为纵轴不一样，第一张图上的1格代表10万人，第二张图上的1格代表20万人。

师（出示有数据但没有横轴信息的统计图，图略）：随着西湖游客越来越多，甲、乙两位船夫也忙得不亦乐乎，谁搭载的乘客多呢？

生3：一样多。

生4：不好判断，因为不知道横轴的数据。

师（在图中补充横轴的数据，如图2-2）：现在你知道了吗？

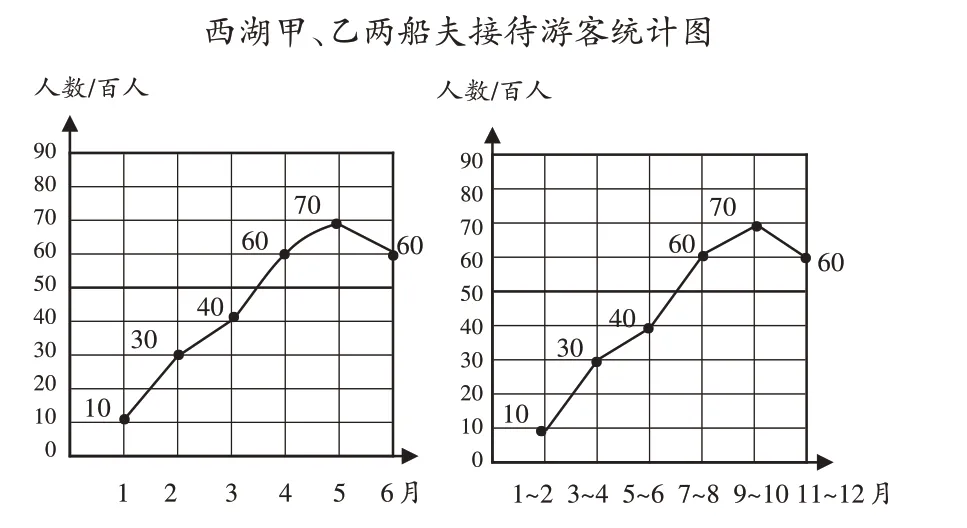
图2-2

师：有些图像看上去一样，但统计数据不同；有些图像虽然有所不同，但是统计的数据却是相同的。在读取图中信息和对比分析时，应该要注意些什么？

生5：不仅要观察图像，更应分析数据。

生6：标准要统一。

数学建模的价值在于从研究实际问题出发，整理、提炼出数学策略。学习本课之前，学生已经接触过统计图，但是在问题解决的过程中容易忽略统计图的一些要素，缺乏整体的思考和细节的关注。本案例利用现实情境提醒学生分析问题不仅要观察图像，还要统一标准。

（2）积累表象，打好建模基础

教师在教学时要给学生提供必要的物体、模型和图形等，为学生的思维活动提供必要的素材，帮助学生将实物与抽象的符号联系起来，进而构建数学知识。

【案例2】以“分数的意义”为例，教师在引领学生分单一的图形或物体的四分之一的基础上，给学生提供10个圆片，让学生任选几个进行平均分，找出四分之一。

学生有多种分法：有的选择了偶数个，有的选择了奇数个，有的是先把每一个圆片平均分成四份后选择每个圆片的四分之一，有的把所有的圆片看成整体后再平均分成四份……学生通过实际操作，能对单位“1”有更深层的理解和体悟，从而自主建构分数的意义。

对此，教师可通过问题“每个图形被涂色部分的大小、个数、形状都不相同，为什么都可用来表示四分之一？”引导学生思考后呈现数学模型（如图3）。

图3

出示练习：（1）说说你对“我国小学生中，睡眠不足的人数大约占总人数的”的理解。（2）猜一猜图4中涂色部分有几个苹果，为什么？

图4

拼、摆等操作可以将抽象的问题形象化，更利于空间想象能力比较弱的学生。

（3）抽象本质，正确构建模型

数学学习的核心是感受和领悟知识的本质，教师要善于激励学生主动思考，引导学生理解数学知识的本质，帮助学生构建问题解决的模型。

【案例3】教学“乘法分配律”时，教师可给出3道不同的习题以引导学生发现不同情境问题与数学算式间的共同规律，然后再揭示乘法分配律的数学模型，这样学生的思维能得到提升和发展，学生对学习的知识也印象深刻。

数学抽象，是先让学生亲身感受到数学知识的产生过程，帮助学生获得数学概念和规则，形成数学思想和方法，再抽象出必要的数学模型，最后加以解释和应用，这就是一个建模学习的过程。通过建模学习，能不断增强学生从数学的视角来分析、思考和解决问题的能力。

2.优化建模——发展思维，提升能力

（1）深度挖掘，构建有效模型

建构主义认为，数学学习不是知识从外到内的简单传递，而是学生积极主动地建构知识和积累经验的过程。因此，教师要设计具有一定思考价值的数学问题，帮助学生构建有效的数学模型。

【案例4】被除数、除数、商，如果其中一个量或两个量变了，还有一个会怎么变？

呈现：

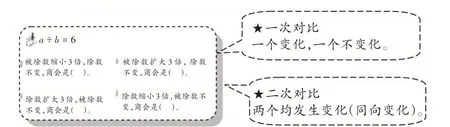
学生举例验证，教师根据学生的总结进行归纳。

拓展：

达成共识：被除数和除数同时增加相同的倍数，商不变。

层层递进的多样素材和情境问题能激发学生深入思考、主动探究。

（2）拉伸长度，升华数学模型

重叠问题的灵魂是集合思想，集合思想的具体表现形式为用集合圈将具有某种特征的数圈在一起。在学生经历了集合从实物阶段向符号阶段抽象的过程后，教师可帮助学生运用熟知的实物来感受数学模型，并且依托数学模型来解决实际问题。

【案例5】如图5，教师引导学生理解算式“8+9-3”的含义，并且理解“-3”的道理，至此初步建立了重叠问题的数学模型。

图5

接下来教师还可以向学生介绍集合圈的数学历史故事，举出生活中的实例，使学生能将所学知识与新情境进行联系，感受数学的魅力。

这样的扩展不仅可以激发学生对数学学习的兴趣，还能培养学生提出、分析和解决问题的能力。

3.活用模型——拓宽思路，破除定式

（1）注重情境创设

通过创设现实情境的方式引入新知识，既能增强数学学习的趣味性，又有助于学生根据情境灵活选择数学模型解题。

【案例6】“鸡兔同笼”问题的拓展

买物品问题：红铅笔每支0.38元，蓝铅笔每支0.22元，两种铅笔共买了16支，花了5.60元。红、蓝铅笔各买了几支？

三个量的问题：蜘蛛有8条腿，蜻蜓有6条腿和2对翅膀，蝉有6条腿和1对翅膀，现在这三种动物共18只，有118条腿和20对翅膀。每种动物各几只？

配制盐水的问题：有甲、乙两种盐水，甲种盐水中含盐4%，乙种盐水中含盐7%。小强要用这两种盐水来配制含盐5%的盐水60千克，可选用甲种盐水和乙种盐水各多少千克？

学生通过某一个问题情境掌握了问题解决的策略，在初步建立了数学模型后，教师可以不断变换情境，检验学生对数学模型的理解和实际运用能力，帮助学生发展和提升数学思维。

（2）适时交流争辩

【案例7】一边靠墙的图形的周长计算问题：图6中的长方形的周长计算是否正确？

图6

在学生列出正确算式“（3+5）×2=16（米）”后，教师可通过问题“如果3+5×2=13（米）成立，那计算的是哪些部分的长度？”引出三组图形周长计算的对比（如图7）。

图7

对于靠墙图形的周长计算问题，学生错误率较高，究其原因是学生对周长的理解不到位。对此，教师需要引导学生通过具体分析来构建正确的模型。开展问题解决教学时，既要结合具体问题情境培养学生建立数学模型的思想，也要避免让学生陷入固化的数学模型当中。因此，要去模型化，使学生能够根据实际问题选择正确的、合适的解题方法。

通过数学建模教学，学生学会了融会贯通知识，更能认识和理解知识的本质规律，能够根据知识的本质特点正确建立数学模型，从而分析、归纳和解决问题。由此可见，在数学学习中进行数学模型思想的培养和数学模型的建构，其价值和意义是深远的。