降雨条件下含夹层边坡稳定性及影响因素敏感性分析

彭金科,童 立

(1.湖南省水运建设投资集团有限公司,湖南 长沙 410011;2.湖南省交通科学研究院有限公司,湖南 长沙 410015)

1 降雨作用下含夹层边坡稳定性演化规律分析

1.1 非饱和边坡稳定性计算理论

土体的抗剪强度理论是分析边坡稳定性的基础。在计算降雨条件下边坡稳定性时，由于土体存在非饱和区域，土颗粒、水、气等三相介质之间将产生微观的相互作用力，如固液界面接触之间的表面张力，这些力将宏观表现为基质吸力。而基质吸力会一定程度上的加强土体抗剪强度，因此传统抗剪强度理论无法适用。国内外学者通过大量实验和理论研究提出了许多非饱和抗剪强度理论，其中Vanapalli等[9]提出的非饱和抗剪强度公式因其计算的非饱和抗剪强度可根据渗流场的变化而实时变化，更能反应边坡土体强度变化而广泛应用。公式如下

τ=c′+(σ-ua)tanφ′+

(1)

式中：τ为非饱和土抗剪强度，kPa；(σ-ua)为净法向应力，kPa；(ua-uw)为基质吸力，kPa；φ′为有效内摩擦角，°；c′为有效黏聚力，kPa；θw为含水量，cm3·cm-3；θs为饱和含水量，cm3·cm-3；θr为残余含水量，cm3·cm-3。

基于上述土体非饱和土抗剪强度理论，即可体现基质吸力对边坡稳定性的影响，进而求解边坡稳定性安全系数。在边坡稳定性分析中刚体极限平衡法成熟，主要有Morgenstern-Price法(简称M-P法)、瑞典圆弧法、毕肖普法和剩余推力法等[10]。相比其他方法，M-P法可适用任意形状的滑裂面，考虑了条块的静力平衡和力矩平衡，可更好体现土条间的实际相互作用，因此采用该方法基于非饱和土抗剪强度理论探究不同雨型降雨入渗下含夹层边坡的稳定性。

1.2 计算模型及工况

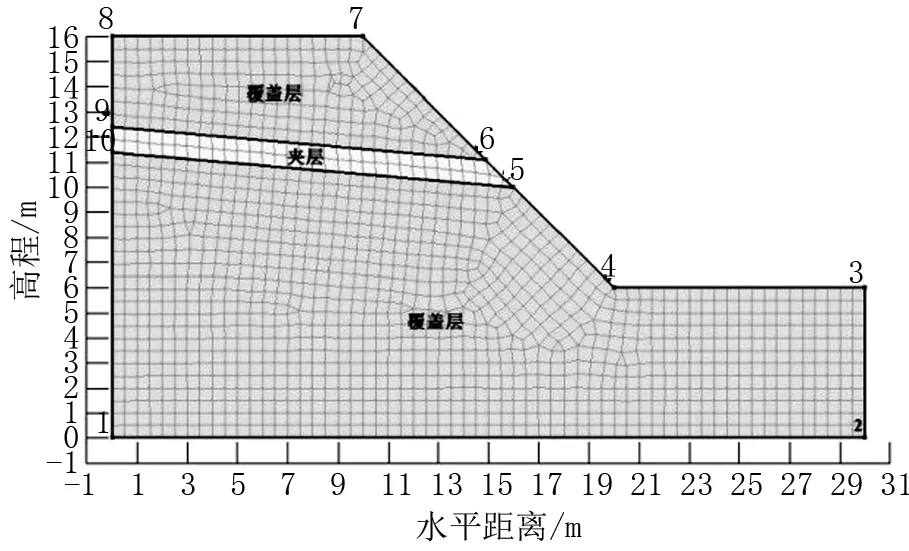
注：1、2、3、4、5、6、7、8、9、10为模型节点序号图1 计算模型示意图

以文献[5]所述京珠高速(长沙―株洲段)公路边坡为依据，概化计算模型，如图1所示，模型结构主要分为：上、下两部分为普通土体、中间为另一类土。其几何尺寸为：坡高10 m，坡宽10 m，坡比为1∶1；基础厚度为6 m，宽度30 m；夹层位于距离底部边界10 m的地方，厚度为1 m，倾角5°。渗流边界条件为：左侧、公路路面和右侧基础部分设置为不透水边界；坡顶和坡面设置为降雨边界。底部设置地下水位线。根据文献[2]选定两种土体材料的土体水力参数如表1所示。计算工况：选择总雨量150 mm，历时24 h的一场降雨。采用前峰、中峰、后峰和均匀型四种典型雨型进行计算，探究不同雨型下含夹层公路边坡稳定性的演化规律。

表1 土体材料物理参数

1.3 结果分析

不同雨型降雨入渗下边坡安全系数随时间演化结果如图2所示。由图可知：针对降雨雨量、历时相同的一场降雨，在雨型不同时，边坡稳定性随时间呈现出不同演化规律：(1)均匀型雨型，边坡安全系数随时间呈近线性减小趋势，这是因为降雨过程中降雨强度一直保持不变，水分持续入渗，降低了边坡的抗剪强度从而导致边坡稳定性降低。(2)前峰型雨型，边坡安全系数先快速减小，在6 h后匀速减小，在20 h后减小速度变小，甚至出现了安全系数回升变大，这是因为前峰型降雨在开始的时候降雨强度大、后面的降雨强度小，使得开始阶段雨水入渗量大、后期小，边坡安全系数也随之变化。(3)中峰型雨型，安全系数先慢后快再慢减小，这是因为中峰型降雨，降雨强度随时间先增加后减小，影响边坡稳定性的雨水入渗量也随此规律变化。(4)后峰型雨型，安全系数先慢后快减小，这是因为后峰型降雨，降雨强度随时间持续增加，导致后期雨水入渗量急剧加大。(5)降雨结束时，各雨型下边坡安全系数由大到小依次为：后峰型、中峰型、前峰型、均匀型，表明在实际工程中，对于含夹层边坡的整体稳定性评判时，应该考虑降雨雨型差异性的影响，针对不同的雨型给出防灾减灾的建议。

图2 不同雨型下边坡安全系数演化图

2 降雨作用下含夹层边坡稳定性影响因素分析

2.1 基于正交试验的影响因素敏感性分析方法

基于正交试验进行影响因素的敏感性分析，因试验数少、使用方便以及分析效率高等特点在各个领域应用广泛。具体方法如下：第一，确定评价的结果指标；第二，根据定性分析确定影响结果指标的主要影响因素及水平；第三，选定正交表格设计试验方案；第四，根据各个方案计算或者试验出结果；第五，基于极差分析法计算各个因素对结果指标影响的量化值。

极差分析原理如下[11]：设i(i=A,B,…)为影响因素，j(j=1,2，…，r)为因素水平数，则因素i的第j水平记为Xij。由Xij下进行试验得到结果指标Yij。记Kij为因素i在j水平下的统计参数，计算公式如下

(2)

式中：n为试验次数；Yijk为因素i在j水平下第k个试验结果指标值。

各影响因素敏感性大小根据极差Ri确定，极差越大该因素对试验结果影响程度越大。计算公式如下

Ri=max{Ki1,Ki2,…,Kir}-min{Ki1,Ki2,…,Kir}

(3)

2.2 正交试验设计

基于上述方法，首先选取边坡安全系数为正交试验的结果指标。同时，将总雨量、降雨历时、雨型、夹层厚度以及夹层倾角等5个主要参数作为控制因素，分别用A、B、C、D、E表示，并以1.2节表1采用的计算参数值为基准概化为4个水平，见表2。

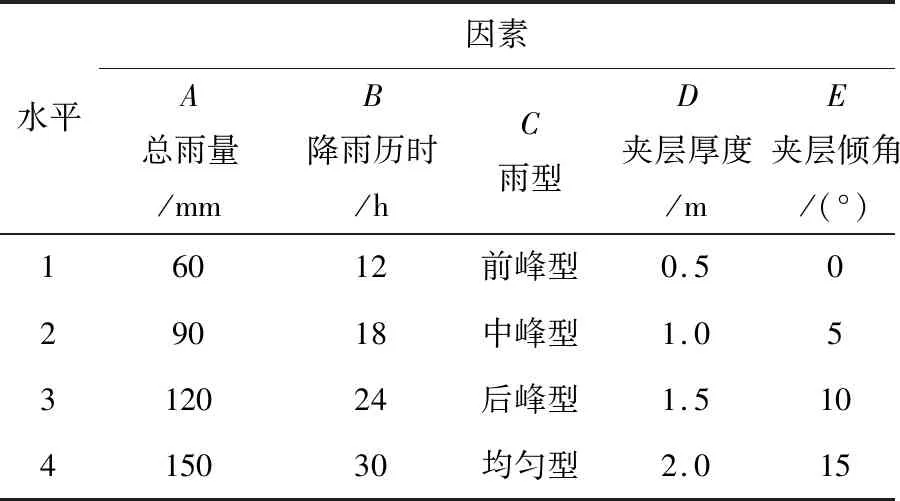
表2 影响因素水平表

2.3 结果分析

根据影响因素个数及其水平，选取5因素4水平的标准正交表，设计16个试验方案。采用M-P法计算各方案下的边坡安全系数，结果见表3。由表可知，边坡的安全系数在各个计算方案下呈现出不同的大小。

表3 正交试验方案及结果表

在上述正交实验计算结果基础上，基于极差分析理论进一步分析得到各影响因素的极差大小，如图3所示，各影响因素的极差由大到小依次为：总雨量、倾斜角度、降雨历时、雨型、夹层厚度。因此可知整体上在这几个因素中总雨量对边坡的稳定性影响最大，夹层厚度影响最小。对于降雨参数而言：总雨量影响最大、降雨历时次之、雨型影响最小。对于夹层几何参数：倾角影响最大，夹层厚度次之。

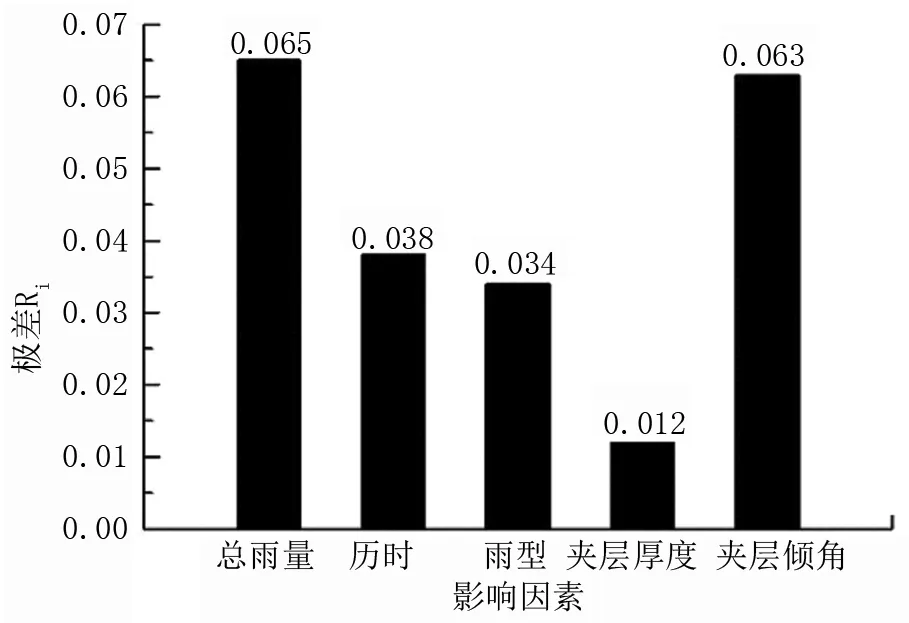
图3 影响因素极差分布图

3 结 论

(1)不同雨型下，边坡稳定性随时间呈现出不同演化规律：均匀型雨型，边坡安全系数随时间呈近线性减小趋势；前峰型雨型，边坡安全系数先快速减小再匀速减小，最后出现了安全系数回升变大。中峰型雨型，安全系数先慢后快在慢；后峰型雨型，安全系数先慢后快减小。降雨停止时刻，各雨型下边坡安全系数由大到小依次为：后峰型、中峰型、前峰型、均匀型。

(2)各影响因素的敏感性由大到小依次为：总雨量、倾斜角度、降雨历时、雨型、夹层厚度。对于降雨参数，总雨量影响最大、降雨历时次之、雨型影响最小。对于夹层几何参数：倾角影响最大，夹层厚度次之。因此在工程实际中，应该重点关注降雨总雨量和夹层倾角这两个因素。