天津市设计暴雨雨型的演变
2020-02-05黄津辉范泽华
黄津辉,王 超,范泽华
(1.南开大学中加水与环境安全联合研发中心,天津 300350;2.重庆交通大学河海学院,重庆 400074; 3.海绵金水(北京)工程设计院有限公司,北京 100089)
海绵城市概念的提出,改变了以往城市雨洪管理以峰值控制为主的设计理念,将城市雨洪管理从峰值管理转向了径流总量的管理和径流过程的控制[1-2]。传统的城市排水系统是根据设计暴雨的极值来设计的,而海绵城市的重要指标年径流控制量和暴雨径流的非点源污染控制,都是以特定时间段内“量”的管理为重点[3]。降雨的时程分布是降水量或者降雨强度在时间上的分配,表征的是降雨过程的变化,也称作雨型。
早在20世纪40年代,苏联学者莫洛可夫等[4]就对雨型问题进行了研究,在分析了乌克兰地区降水资料后,根据统计计算,划分了7种模式雨型。1957年,Keifer等[5]根据降雨强度和历时的关系提出了芝加哥雨型,该雨型对各种历时的暴雨过程都适用。1980年,Yen等[6]提出了一种单峰型的三角形雨型,用于计算小流域排水区域的径流。1967年,Huff[7]在研究美国伊里诺斯州的暴雨后,提出把降雨按雨峰出现位置划分成4类,并利用无量纲累积过程来表示雨型。1975年,Pilgrim等[8]提出把雨峰设置在出现概率最大的时段上,然后将雨峰时段在总雨量中的比例取为各场降雨雨峰所占比例的均值,其他各时段的雨量比例也用相同的方法确定。我国对雨型的研究相对较少,2002年王家祁[9]提出“短推长”和“长包短”两种雨型方法,这两种方法在很大程度上避免了传统以典型暴雨进行频率放大作为设计雨型导致偶然性较大的不足。武晟[10]分析了王家祁雨型方法、三角形雨型和Pilgrim & Cordery雨型的适用性,指出相对于三角形雨型和Pilgrim & Cordery雨型,王家祁雨型更加符合当地实际情况。2011年范泽华[11]利用天津多年暴雨资料和Huff雨型方法给出了天津暴雨雨型的频率分布特征。2018年李志元等[12]给出了多种暴雨雨型在降雨资料充分与否时的推荐方案。
雨型的差异不仅影响降雨的峰现时间,更影响降雨在研究流域中产生的径流总量[13],因此,对于工程设计的径流计算,相应总雨量在降雨过程上的分配,不能简单以一场典型降雨过程为标准,而应当基于当地大量的暴雨资料,在充分研究当地暴雨规律的基础上,选择具有统计规律的设计雨型。
在海绵城市建设的大趋势下,对设计暴雨和设计雨型的研究要求逐渐提高,虽然目前已经有多种设计暴雨和设计雨型的方法,但关于设计暴雨和设计雨型在大型城市随时间的演变规律的研究很少[14]。2013年黄津辉等[15]对天津市多种设计暴雨的方法进行了比较,发现现行的设计暴雨强度不同于根据1951—2004年暴雨数据推求的设计暴雨强度。2017年成丹等[16]利用同频率法研究了宜昌市的设计暴雨雨型的演变特征,发现短历时暴雨的峰值增加持续时间变长。由于防洪排涝水利工程设施等很多是百年工程的设计,设计暴雨和设计雨型等都是这些工程设计的标准[17];对设计暴雨及雨型的不确定性和变化规律进行研究,在设计中就考虑降低风险的措施,对提高水利工程的韧性和长期性能具有重要意义[18-20]。
天津市位于京津冀都市经济圈,是我国北方重要的经济中心,总面积11 916.85 km2,城市建成区面积2 585 km2;截至2018年,总人口1 559.60万人,是典型的超大城市。随着城市快速发展,城市面积扩展迅速,这极大地改变了该地区的水文循环、水量平衡和能量平衡,城市开发的水文效应显著。由于大城市人口密度大,公共和私人财产高度聚集,城市系统的脆弱性高,研究大型城市降雨统计规律,研究其设计暴雨和设计雨型,可为城市风险控制、城市规划设计、城市建筑物和基础设施建设等提供参考[21]。目前世界上对大城市暴雨雨型及雨型演变的研究不多,且不充分。天津市是位于北方沿海地区的大城市,对其雨型演变规律进行研究,有很强的典型性和借鉴意义,可为其他超大城市的建设和管理提供参考。
1 资料与方法
1.1 数据来源
本文所用暴雨资料来自天津市气象局,为塘沽气象站1951—2004年共54年的逐分钟暴雨资料,是对天津市气候监测站降水自记纸记录进行信息化处理后得到的数据,每年选取前3场最大暴雨,共计162场暴雨资料。暴雨资料涵盖年限长、样本量大,降雨序列包含的暴雨极值代表全面,能够较好地反映实际暴雨过程。
1.2 Huff雨型
1967年Huff[7]利用伊利诺斯州中东部的49个雨量站1955—1966年的降雨数据对降雨时程进行了分析,并根据降雨峰值出现在一场暴雨中时程区间的不同,将降雨时程分布划分成4种降雨类型,降雨峰值出现在降雨历时的第几个四分之一时段,就称为第几四分之一雨型。研究表明,降雨峰值大多出现在前两个四分之一区间内。1990年Huff[22]又利用伊利诺斯州其余12个雨量站和芝加哥地区的6个雨量站研究了点雨量和面雨量的时程分布,指出概率水平为50%的降雨过程最适合实际情况,峰现越早、峰值越高的暴雨时程分配对城市排水系统的压力越大,风险越高。
1.2.1降雨场次划分
本文根据天津市气象局多年实测降雨分钟记录以及天津市的降雨特点,确定天津市的降雨时间间隔阈值P为12 h。如果降水量很小,则很难形成径流,所以本文对用于推导雨型的场次雨量设置了阈值。参考中国气象局对降雨强度等级划分标准,设置场次降水量的阈值为2 mm。根据以上标准,对塘沽气象站1951—2004年164次暴雨资料进行暴雨场次划分,得到172场满足标准的降雨,降雨历时在3~50 h之间。
1.2.2Huff雨型推导方法
a. 总雨型。将172场降雨中的第n场的降水量记为Sn,xni表示第n场降雨中第i分钟降水量;对第n场降雨按照降雨历程进行十等分,每一段时间的降水量分别记为xn1、xn2、……、xn10。分别计算每一段时间内水量占总降水量的百分比,得到172场降雨每段降水量占总降水量的百分比;对每一段降水量百分比按照降序排列,然后按照经验频率计算排序后的频率,分别提取10%、20%、……、90%对应的降水量占比。
b. 4类Huff雨型。根据降水量峰值出现时间在一场降雨历时的位置,将降雨时程分布划分为4种降雨类型(第一四分之一、第二四分之一、第三四分之一和第四四分之一雨型)。根据峰现时间把暴雨过程归类后,重复总雨型的计算步骤即可得到不同类型的Huff雨型。
1.3 时段雨型计算
时段雨型的计算需要选取特定降雨历时的降雨事件,根据总雨型的计算流程计算该降雨历时下的雨型,即为某历时的雨型。一般选用的时段雨型的降雨持续时间分别为1 h、3 h、6 h、12 h以及24 h。1 h 雨型是指根据降雨时间小于1h的降雨数据得到的雨型;3 h雨型是指根据降雨时间1~3 h的降雨数据得到的雨型;其他类推。时段雨型的计算方法参考总雨型的推导方式。
2 结果分析
2.1 天津市Huff雨型
根据Huff雨型推导方法,推求了天津市的Huff总雨型,如图1所示。将降雨时间序列按雨峰出现位置的不同划分成4类,对各类降雨进行归类,进而得到各类雨型的平均无量纲累积过程。图2为4种Huff雨型无量纲降雨时程分布累积曲线。由图2可以看出,第一四分之一雨型和第二四分之一雨型差别较大,而第三四分之一雨型和第四四分之一雨型变化不明显。概率水平为90%的曲线所表征暴雨的降雨时程分布雨峰相对其他频率来讲有滞后和平均化的趋势,也是风险较小的时程分布形式。概率水平越小的暴雨过程,出现的概率越小,也越极端。从图2可以看出,概率水平小的暴雨过程,其峰值出现的时间早,且峰值高,暴雨来的迅猛,所代表的暴雨雨型风险度大。从4种Huff雨型的各频率降雨过程可以看出,概率水平为10%的降雨过程相对其他频率的降雨过程累积降水量占比上升最快。
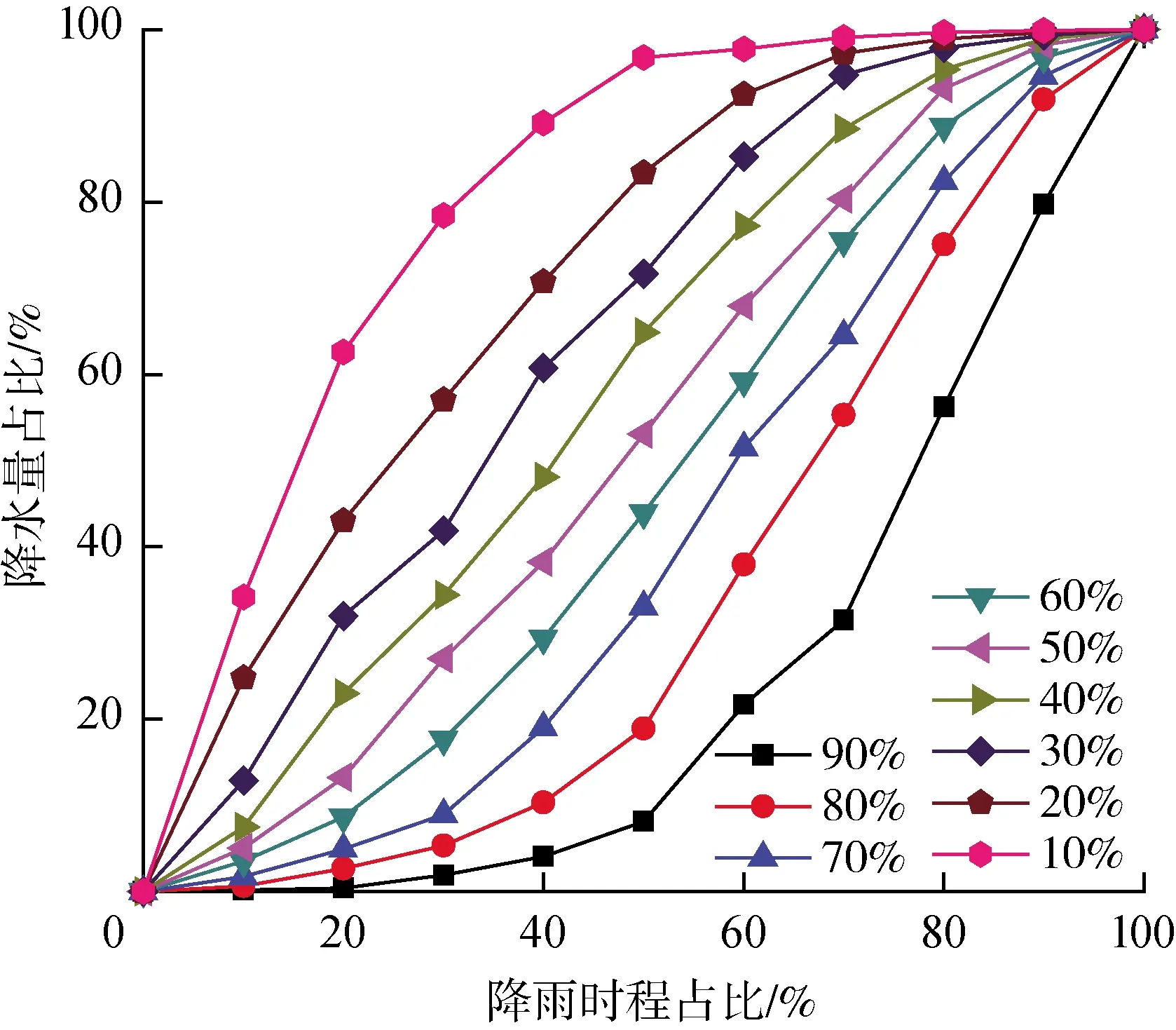
图1 天津市Huff总雨型


(a) 第一四分之一雨型

(b) 第二四分之一雨型

(c) 第三四分之一雨型

(d) 第四四分之一雨型
图3是分别根据第一、第二、第三和第四四分之一雨型概率水平为50%的数据所绘制的无量纲累积降水量占比随时程变化。从图3可以看出,第一和第二四分之一雨型在降雨时程占比为50%时出现了交叉的现象。该现象表明,第一四分之一雨型的降水量分配在降雨时程的前期更为集中,而第二四分之一雨型在降雨时程的中后期其降水量比第一四分之一雨型的降水量要多。

图3 第一、二、三、四四分之一雨型50%概率水平累积降水量占比
2.2 天津市时段Huff雨型
根据时段雨型的计算方法,分别计算了6 h、12 h、24 h的雨型,结果如图4所示。从结果来看,概率水平为10%的累积降水量占比在降雨时程的前期升高最快,在降雨历时的第一个四分之一时段内就达到了95%左右,说明概率水平为10%的降雨过程降水量主要集中在前期,而概率水平为90%的累积降水量占比增加速度最慢,累积降水量占比最晚到达100%。因此,相对而言,概率水平为10%的降雨过程对城市排水系统的压力更大,更容易引起城市内涝。由于概率水平为10%的降雨过程峰现时间早,加之城市不透水面积大、降雨汇流速度快,使得雨峰有更大概率落在汇流时间内,或者使汇流时间内总降水量比其他频率雨型的总降水量大,最终会导致更大的径流量,增大城市排水系统的压力,增加了城市内涝的风险。
2.3 天津市Huff雨型的年代际变化
为了直观地分析比较天津市暴雨雨型的年代际变化,将天津市1951—2004年暴雨资料分为前 27年(1951—1977年)和后27年(1978—2004年)两个时期,分别计算前后两个时期的24 h雨型。对比前后两个时期暴雨雨型的累积降水量占比后发现,除了概率水平为10%的24 h雨型变化不大,后27年雨型其他所有概率水平的24 h雨型前期降水量都增加,累积降水量占比随降雨时程的增加速度更快。表1为各概率水平下前后两个时期在第一个四分之一时段内的累积降水量占比,可以看到后27年在所有概率水平下第一个四分之一时段内的累积降水量占比都大于前27年。

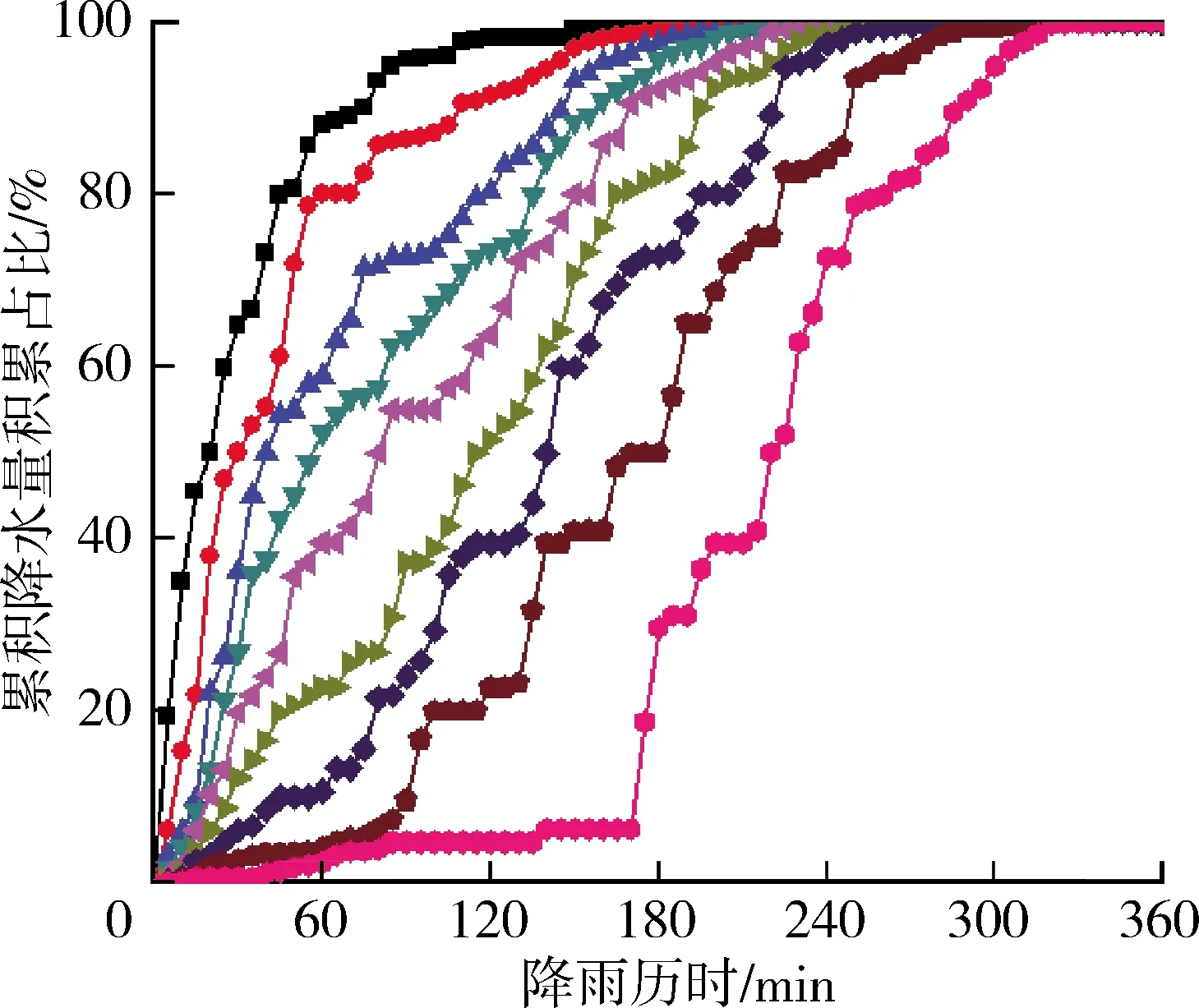
(a) 6 h雨型

(b) 12 h雨型

(c) 24 h雨型
表2展示了天津市前后27年两个时期概率水平为50%的6 h暴雨雨型降水量占比随降雨时程分布情况。从表2可以看到,相对于前27年,后27年暴雨雨型发生了显著的变化:首先,后27年暴雨雨型的雨峰出现在第40分钟占总降水量的26.8%,而前27年暴雨雨型的雨峰则出现在第200分钟占总降水量的15%,雨峰峰现时间大大提前;其次,在降雨历时的前四分之一时段内前27年雨型的累积降水量占比为28.98%,而后27年雨型的累积降水量占比则达到了68.15%,说明降雨重心沿时程发生了显著的提前;从表2可以看出前27年降雨资料获得的雨型,其雨量分配比较均匀,而后27年雨型则呈现明显的单峰型分布,降水量集中在降雨历时的前期。总之,经过对比天津市前后两个时期暴雨雨型的变化,发现后27年暴雨雨型在前期的降水量出现明显增加,降雨峰值的出现时间明显提前。天津市暴雨雨型的年代际变化说明,由于多种因素的影响,包括城市开发对水文效应的影响以及气候变化的影响,暴雨的时程分布也在发生变化,因此在城市开发建设和海绵城市建设的推进工作中,应注意推求设计雨型所用暴雨资料的更新,方能获得更符合当下特点的设计雨型。

表1 24 h雨型各概率水平下在第一个四分之一时段内累积降水量占比

表2 前后27年概率水平为50%的6 h暴雨雨型降水量占比随降雨时程分布
2.4 雨型变化对径流和年径流总量控制率的影响
为了研究雨型发生变化情况下城市区域径流量的响应情况,用总降水量为25.4 mm、不同时程分布的场次降雨来验证同一个城市区域的产汇流情况。把2.3节中得到的天津市前后两个时期概率水平为50%的6 h时段雨型作为两个降雨方案,把两种雨型的时程分布占比乘以一个固定的降水量(25.4 mm)生成两种降雨时间序列方案(分别为前27年6 h设计暴雨雨型和后27年6 h设计暴雨雨型)。城市区域选择天津滨海新区的一个面积为22.8 km2、不透水率为78.6%的成熟的开发区。图5 是这个区域的SWMM模型,将区域分成了604个汇水分区,模拟了608个管道。在后27年6 h设计暴雨雨型下的径流量峰值为42.01 m3/s,峰现时间为1:40,径流总量为295.8×103m3。而在前27年6 h设计暴雨雨型下径流峰值为42.91 m3/s,峰现时间为3:00,径流总量为266.2×103m3。以上结果表明,在降水量相同的情况下,由于暴雨雨型的改变使雨峰提前,导致径流的峰值相应提前了1 h 20 min,径流总量也增加了。而暴雨径流峰值的提前会缩短应对暴雨采取措施的时间,增加暴雨洪水的风险。
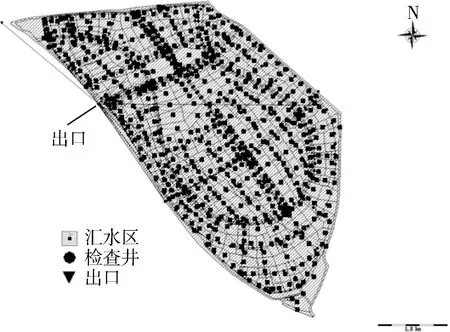
图5 SWMM模型模拟的城市区域
3 结 论
a. 对天津市1951—2004年暴雨雨型的统计结果表明,天津市暴雨的大部分雨量集中在较短的时间内,且雨峰大多出现在第一个四分之一和第二个四分之一降雨时程内。
b. 相对于前27年,天津市后27年6 h雨型累积降水量占比增加更快,前期各概率水平下的累积降水量都要更高,前期降水量占比也更大,势必增加城市径流量,增大城市管网的压力。
c. 天津市前后两个时期的设计暴雨雨型发生了明显的变化,受此影响,暴雨径流过程的峰现时间提前,洪峰流量增长,径流总量也相应增加。
d. 设计暴雨雨型不是一成不变的,天津市设计暴雨雨型发生了变化,使得雨峰前移、暴雨径流峰值变大,城市管网排水压力增大,从而增加了城市内涝的风险。因此,海绵城市规划设计时应及时根据最新资料更新设计暴雨雨型,得到最符合当下情况的设计雨型,从而对海绵城市建设工作做出更有效的指导。
