基于模拟退火与网络单纯形法的通信网络中设施选址优化算法

汤 定 一

(复旦大学软件学院 上海 200433)

0 引 言

随着互联网行业的发展，在线视频网站用户数量和用户时长快速增长，使用移动设备获取视频服务已成为众多用户的习惯。视频内容需要消耗较多流量，影响用户体验的关键在于带宽。视频内容从视频网站到用户需要如下过程。首先，视频存储在视频服务提供商的多个服务器中。当用户请求视频时，视频服务提供商选择城市通信网络中距离用户较近的服务器，通过链路将内容发送给用户。最后，用户收到视频进行观看。为了确保用户在观看视频时不会经常卡顿，需要满足用户所需带宽。

视频服务提供商在提供视频服务时，需要考虑服务器硬件成本、部署成本和带宽租赁费用。在满足所有用户需求的前提下，选择服务器部署节点集合、带宽租赁方案，使得总成本最低。

在城市通信网络中提供视频服务在概念上与内容网络类似。内容网络通过在Internet上部署服务节点，并通过应用层协议将这些服务节点组织形成一个构建在IP网络之上的覆盖层，为用户提供灵活高效的服务[1]。

服务节点部署一直是学术界和工业界研究的热点问题。文献[1]将服务节点部署归纳为选址问题，根据所需获得的信息不同，分为三类：基于确定信息的选址、基于概率模型的选址和基于博弈论的选址模型。

这里重点讨论与本文问题相关的基于确定信息的模型，即已知网络拓扑和部署费用等信息。

基于确定信息的选址模型包括两种设定：设施选址问题[2]和P中心问题[3]，它们的区别在于是否限定设施数量。如果候选地点建站成本允许不相等，那么称为无容量限制设施选址问题(UFLP)，这时可用建站成本来扩展目标函数。在Mirchandani等[4]和ReVelle等[5]的文章中可以找到关于UFLP问题的广泛研究。

Goldengorin等[6]提出了增强的分支界定算法解决无容量限制设施选址问题，最小化部署成本与距离组成的混合指标。Tcha等[7]提出了基于分支界定的方法解决多层无容量限制设施选址问题，适用于具有多层结构的内容网络。这两个工作都使用整数规划类算法，在约束条件较少、模型较简单时能够计算出最优解。但是，实际应用场景中通常需要考虑的数据规模较大，约束条件也更为复杂，此时整数规划类算法的时间复杂度剧增，难以满足实际应用需求。

Radoslavov等[8]从考虑路由拓扑的角度使用贪心算法解决服务器选址问题，优化目标为平均延迟和网络容量。Laoutaris等[9]使用分布式和可扩展的方式解决内容分发网络中服务节点选址问题。脱立恒等[10]提出两种贪心启发式算法解决服务器节点部署问题，在保证平均转发延迟的前提下最小化服务部署规模。史佩昌等[11]使用启发式算法求解多维设施选址模型。Berman等[12]使用贪心启发式算法解决网络中位置覆盖问题。这些工作使用贪心和启发式算法，优点在于能在较短时间内给出较优解，不足之处在于贪心算法通常容易陷入局部最优解，而难以收敛到全局最优。

综上所述，现有工作通常使用整数规划类算法和启发式算法。然而，对于通信网络中提供视频服务的问题，难点在于：(1) 网络和节点规模较大；(2) 在考虑服务器节点部署和网络带宽费用的基础上，加入了服务器档次的选择。现有的整数规划类算法不能在短时间内得出结果，而现有的启发式算法通常缺乏普适性难以高效地解决此问题。因此，本文提出一种两层迭代算法对该问题进行高效求解：外层为设施选址问题，通过模拟退火方法迭代选址方案。内层在给定服务器部署方案的情况下通过将网络中带宽租赁问题建模为费用流问题，使用网络单纯形求解。通过迭代产生新的部署方案以及计算该方案的总费用，在满足带宽需求的前提下寻找更优的服务器部署和链路租赁方案。该模型采用模拟退火算法，解决了贪心算法过早收敛到局部最优解的问题。网络单纯形法能够快速计算方案，使得整个算法在短时间内能够通过大量迭代得到更优解。在采用模拟退火和网络单纯形算法的基础上，本文创造性地提出分段迭代的方法。根据算法迭代前期和后期服务器位置和服务器档次的选择对于解的优劣的影响程度不同，将算法迭代分为粗调和精调两个阶段，使得算法能够在短时间内得到更优解。仿真结果表明，模拟退火-网络单纯形方案与贪心-Dinic算法相比，能够减少10%以上的总成本，且随着数据规模的扩大，优势更加明显。

1 问题描述

考虑以下通信网络的设施选址问题。城市的通信网络由节点和链路构成，其中每个节点的地位是等同的，它们可以通过链路将收到的数据转发给另一个节点。整个网络可以看作一幅无向图，即数据的传输没有方向的限制。同时这个网络也是连通图，即图中任意两个不同的节点之间存在路径。图中的一些节点有视频带宽需求，即这些点与小区邻近，需要满足用户的需求的视频带宽，称这些节点为消费节点。需要在网络中选择一些节点部署服务器，视频由服务器通过网络推送给消费节点。目标是寻找最优的视频服务器部署方案，在满足所有消费节点的视频带宽需求的前提下，使得服务器部署成本与网络带宽租用成本之和最低。

2 模型建立

本模型旨在满足所有消费节点的视频带宽需求的前提下，使得服务器硬件成本、部署服务器成本和网络带宽租赁的总成本最小。

2.1 模型假设

(1) 每条链路有带宽上限，按照占用带宽收取带宽租赁费，不同链路的带宽上限与单位带宽租赁费可能不同。

(2) 同一条链路的上行、下行方向的带宽上限相互独立，且上下行带宽上限与单位带宽租赁费相同，如带宽上限5 Gbit/s，若上行占用带宽3 Gbit/s，下行可用带宽仍为5 Gbit/s。

(3) 一台服务器可以服务多个消费节点，一个消费节点也可以从多个服务器获取视频内容服务。

(4) 每个节点上最多只能部署1台服务器。

(5) 每台服务器能提供的视频输出能力有上限，分为若干档，不同档位服务器的输出能力与硬件成本不同。随着档次的提升，扩充单位容量的费用单调递增。如从1档到2档输出能力提升25，硬件成本增加200，若从2档到3档输出能力提升25，则硬件成本至少增加200。

(6) 对于每个节点，部署服务器需要部署成本，不同节点的部署成本可能不同。部署一台服务器到一个节点的成本为硬件成本与部署成本之和。

(7) 不同消费节点的带宽需求可能不同。

(8) 服务器可以直接部署在消费节点，对于消费节点来说，该节点上服务器提供的带宽没有链路租赁费用，但该服务器向其他消费节点提供的视频输出能力上限相应减少。

(9) 链路带宽上限与单位带宽租赁费、服务器硬件成本与输出上限、每个节点的服务器部署费、消费节点的带宽需求均为整数。

2.2 约束模型

(1) 决策。xi表示是否在节点i上部署服务器，yi表示节点i上部署服务器的档位。

xi∈{0,1},yi∈{0,1,…,k}

(1)

(2) 目标函数。引入超级源点S和超级汇点T。S向所有部署了服务器的节点i(xi=1)连边，容量为相应服务器档位输出能力cap(yi)，费用为0。所有消费节点i向T连边，容量为需求的带宽di，费用为0。

目标为最小化服务器部署费、链路带宽租赁费与服务器硬件成本之和。

式中：deployi为在节点i部署服务器的费用；fij为节点i到节点j实际占用的带宽。

(3) 约束条件。流量守恒，所有节点(除了S、T)的流入流量与流出流量相等。

流量上限，每条边的流量不超过容量上限。

fij≤biji,j∈N

服务器输出上限，每台服务器输出的流量不超过档位对应的容量。

fSi≤bSii∈N

消费节点满流，每个消费节点的带宽需求都需要满足。

fiT=biTi∈N

(4) 模型参数。N为通信网络中节点集合。S为加入的超级源，T为加入的超级汇。hardware函数表示档位对应硬件成本，cap函数表示档位对应输出能力。bij表示节点i到节点j的带宽上限，根据模型中链路上下行带宽上限相等假设，有bij=bji，i,j∈N。rij为节点i到节点j的单位带宽租赁费。bSi为超级源S到节点i的带宽上限，代表节点i上部署服务器的视频输出能力。biT为节点i到超级汇的带宽上限，代表节点i的视频带宽需求。

(5) 变量。fij，i,j∈{N,S,T}代表节点i到j的链路实际占用带宽。xi∈{0,1}代表节点i是否部署服务器。yi∈{0,1,…,k}代表节点i部署服务器的档位，共k个档位可供选择，其中0档代表没有部署服务器。

3 算 法

本文将问题分为两部分：1) 在网络节点中选择服务器部署节点集合与服务器档位。2) 根据服务器部署方案求最小网络租赁费。其中第一个问题由两层NP难问题组成，第一层是在网络节点中选取服务器部署点集，属于设施选址类问题，属于NP难问题；第二层是确定服务器的档次，比如已经选择在30个节点上部署服务器，服务器可选档次共10档，因此，即便确定了服务器的数量和部署点集，还需要考虑1030种可能档位组合。第二个问题可用费用流在多项式时间求解。

如何高效快速地得到较优解面临两个挑战：(1) 外层算法的选择，需要在速度和全局优化能力之间进行权衡。(2) 内层费用流算法的选择，由于已有多项式算法，需要速度足够快。

对于第一个挑战，有两种类型的算法，遗传算法维护一定数量的解，通过使用交叉、变异等算子进行迭代，推动种群的进化。其优点是全局优化能力强，但速度较慢。贪心算法从一个初始可行解出发，通过迭代优化当前解，优点是速度快，但容易陷入局部最优。我们使用模拟退火算法，具备贪心算法速度快的优点，同时又能通过策略跳出局部最优解。

对于第二个挑战，主流的费用流算法分为增广算法(如Dinic算法)与消圈算法(如网络单纯形)。网络单纯形算法在本文问题的费用流构图中更快。

我们在采用模拟退火和网络单纯形算法的基础上，提出分段迭代的方法进行优化。根据算法迭代前期和后期服务器位置和服务器档次的选择对于解的优劣的影响程度不同，将算法迭代分为粗调和精调两个阶段，使得算法能够在短时间内得到更优解。

3.1 外层模拟退火

模拟退火算法[13]能有效地在一个大的搜索空间中寻找最优解。其包含两个部分：Metropolis算法和退火过程。Metropolis算法用于跳出局部最优解，通过重要性采样方法，以概率来接受新状态。退火过程通过调节初始温度与退火速率，确保目标函数能够在有限的时间内收敛。

模拟退火算法的流程是首先构造一个初始可行解，然后不断迭代“产生新解，计算目标函数，接受或放弃新解”这个过程。通过设置初始温度与退火速率得到当前温度T，然后根据新解相对当前解的代价函数增量计算接受新解的概率。当温度低于给定值或程序运行时间达到预设值时停止迭代。

1) 初始解的构造。令xi∈{0,1}表示编号为i的节点是否部署服务器，yi∈{0,1,…,k}表示编号为i的节点部署服务器的档次。初始解的构造方式为所有节点均部署最高档次的服务器，显然，如果图中存在可行解，则初始解一定是可行解。

2) 新解产生策略。根据当前服务器的部署方案产生新的服务器部署方案，随机采用以下6种策略：(1) 随机选取1个没有部署服务器的节点，在其上新增服务器；(2) 随机选取1个已经部署服务器的节点，撤掉其服务器；(3) 随机选取1个部署了服务器的节点，将其上部署的服务器移动到相邻节点；(4) 随机选取1个已经部署服务器的节点，将其服务器档次提级；(5) 随机选取1个已经部署服务器的节点，将其服务器档次降低；(6) 随机选取2个已经部署服务器的节点，交换两个服务器的档次。

3) 初始温度与退火速度。初始温度影响迭代的有效性和避免陷入局部最优解的能力，过高则增加迭代次数，过低会影响解的质量。采用初始解总成本乘以常数K，这里使用0.01。退火速率采用指数式下降方式：T(n)=λT(n-1),n=1,2,3,…。其中：T(n)为当前的温度；λ为衰减速率；T(n-1)为上一步的温度。

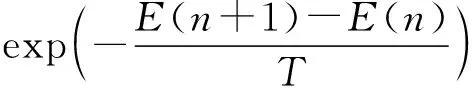
3.2 内层网络单纯形

在给定服务器部署方案时，网络链路带宽租用问题可以建模为费用流问题。

费用流，也称最小费用最大流，是指在网络流图中，每条边除了流量上限外，也有单位流量费用，求出一组可行解，使得满足它是最大流的情况下，总的费用最小。

费用流建图过程如下，首先，费用流图中点集为通信网络中所有节点。由于链路是无向边，在建边时将每条从节点s到节点t的链路拆分为2条边：s到t的边，流量为带宽上限，费用为单位带宽租赁费。t到s的边，流量和费用与s到t的相同。加入超级源点S与T。其中：S与所有部署服务器的点建边，流量为服务器输出带宽，费用为0。所有消费节点与超级汇点T建边，流量为带宽需求，费用为0。如果求得的最大流等于所有消费节点的带宽需求之和，则为可行解。

网络单纯形法[14]采用消圈思想，首先构造一条从超级源S到T的边，流量大于从S流出的所有边的流量之和，也大于流入T的所有边的流量之和。它的费用大于所有边的费用之和。这时如果在原网络中找到任意一条从S到T的路径，将S到T的边的流量导入这条路径，总费用必然减小。求最小费用的过程是不断地在网络中寻找负环，直到找不到负环时得到最小费用。

3.3 分段迭代优化

在算法迭代的初始阶段，服务器的位置选择是影响总成本更重要的因素。而在算法迭代的后期，服务器档次选择为与服务器位置选择同等重要。我们将模拟退火分为两个阶段：粗调阶段和精调阶段。

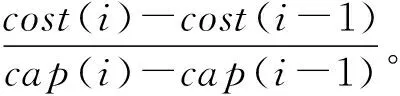
(2) 精调阶段。在精调阶段，模拟退火在构造新解时，同时考虑服务器位置与档次的选择。此时使用原本的费用流图，即超级源连向服务器部署节点的边，容量为cap(yi)，费用为0。在新解产生策略上，使用全部6种策略，特别是在随机时更多选用后3种关于服务器档次的策略。

4 仿真实验

通过在两种不同规模的网络上进行实验，在90 s内将模拟退火-网络单纯形算法给出的方案与贪心-Dinic算法得到的方案进行对比，说明模拟退火-网络单纯形方案能在给定时间内得到显著优于贪心-Dinic算法的解。

4.1 数据集

在两种规模的数据上进行实验：

(1) 中等规模，节点数600，边数2 000左右，消费节点240个。

(2) 大规模，节点数1 200，边数6 000左右，消费节点480个。

其中链路总带宽与网络租用费为[0,100]的整数，视频服务器档次数不超过10个。视频服务器输出能力为不超过300的整数，节点部署服务器成本为不超过2 000的整数，消费节点的视频带宽需求为不超过200的整数。

图1中，通信网络包含50个节点，其编号从0开始。其中：黑色节点为消费节点，比如7号节点是消费节点，有带宽需求；边的粗细表示链路容量，较粗的边比如左上角22号与23号之间的边的可用带宽上限较大，较细的边比如8号到9号之间的边容量较小。

图1 通信网络结构

4.2 对比实验

在两种规模的数据上各使用10组随机数据进行对比。将模拟退火-网络单纯形算法在90 s以内给出的方案与贪心-Dinic方案进行对比。这里选择贪心算法作为传统启发式算法的代表，选择Dinic算法[15]作为通用的费用流算法进行实验对比。

图2展示的是中等规模数据上两种算法在90秒以内给出的方案在总成本上的对比。在第一组数据中，本文算法给出的方案总成本为199 063，贪心-Dinic法得到的总成本为227 604,差距百分比12.5%。在所有的10组数据上，本文算法给出的方案相比贪心-Dinic法的总成本减少10.2%到16.9%，特别是第2组数据，本文算法相比贪心-Dinic法总成本减少了16.9%。

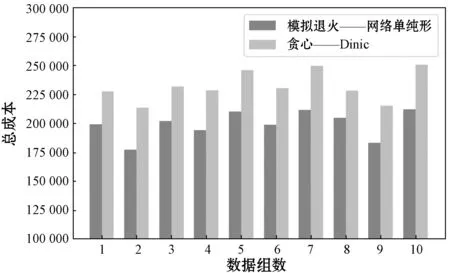
图2 中等规模数据(总共10组数据)上模拟退火-网络单纯形方案与贪心-Dinic方案的总成本对比

图3展示的是大规模数据上两种算法在90 s以内给出的方案在总成本上的对比。在所有的10组数据上，本文算法给出的方案相比贪心-Dinic法总成本减少了19.3%到25.2%。对比中等规模数据与大规模数据上两种算法的总成本差距百分比，可以得出结论，随着数据规模的增加，模拟退火-网络单纯形法相比贪心-Dinic法的优势更大。这主要是由于随着数据规模的增加，解的空间指数级别增大，得到更优解的难度也随之增加。这说明本文算法在不同规模的数据上具有高效性。

图3 大规模数据(总共10组数据)上模拟退火-网络单纯形方案与贪心-Dinic方案的总成本对比

通过在两种规模各10组数据上的对比实验，说明本文方案可以在给定时间内得到总成本显著优于贪心-Dinic法的方案。在实际应用场景中，我们能够快速给出方案以对实际部署提供指导。

4.3 两阶段优化的有效性

下面通过两种不同规模数据的实验，说明两阶段模拟退火算法的有效性。

首先，以中等规模第一组数据举例。如图4所示，在粗调阶段，在前1 000轮迭代内，总成本快速地从45万(千元)下降到20万(千元)，并在接下来的1 000次到8 000次迭代中在20万(千元)左右持续优化。如图5所示，在精调阶段，在前5 000轮迭代内总成本快速从20万(千元)优化到19万(千元)，并在接下来的5 000到38 000次迭代中持续优化。

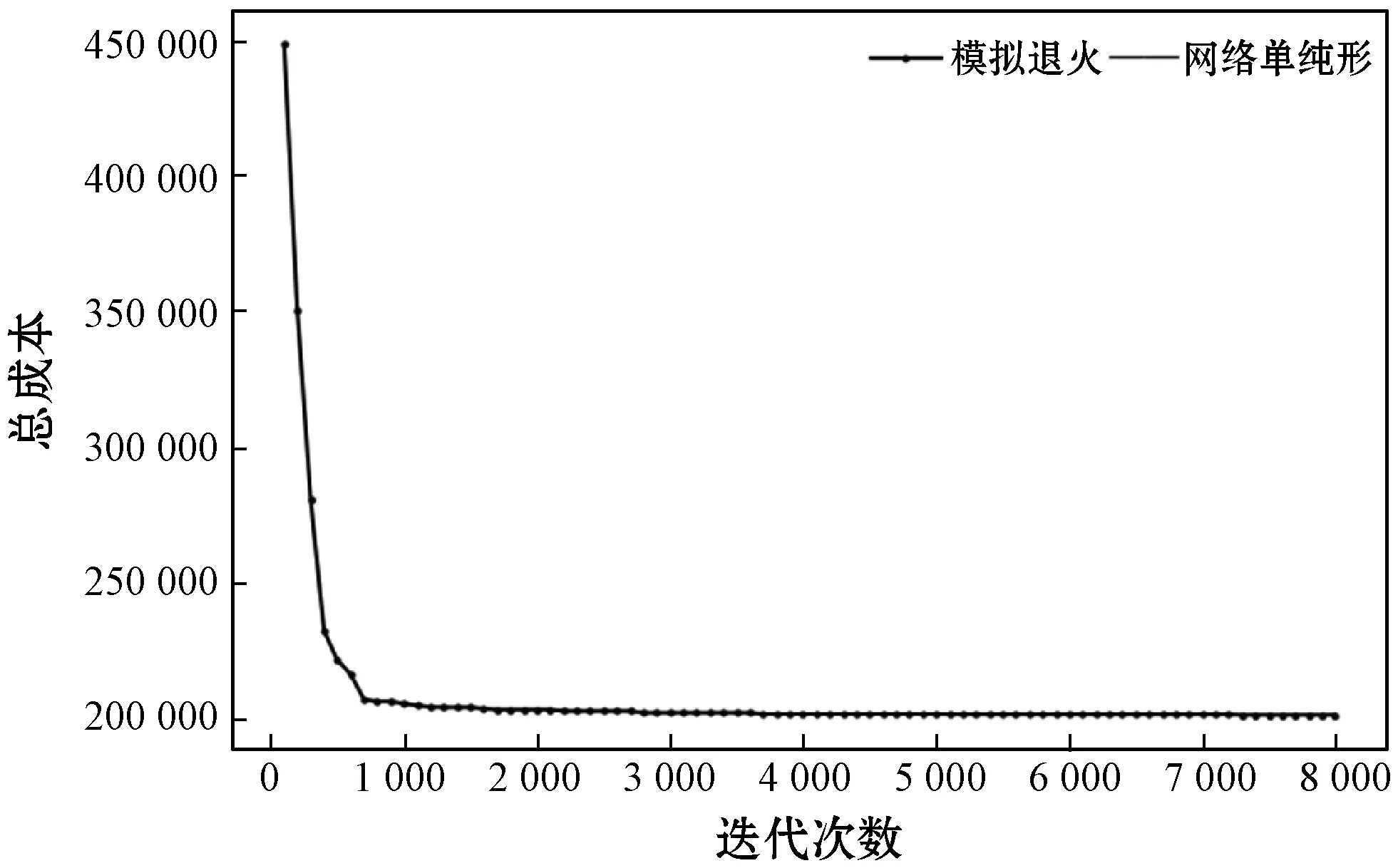
图4 中等规模第一组数据在粗调阶段总成本随迭代次数变化曲线

图5 中等规模第一组数据在精调阶段总成本随迭代次数变化曲线

然后，以大规模第一组数据举例。如图6所示，在粗调阶段，在前1 000次迭代内，总成本快速从1百万(千元)降低到40万(千元)，并在1 000次到3 500次迭代中持续优化。如图7所示，在精调阶段，总成本在前5 000次迭代快速从40万(千元)优化到39万(千元)，并在5 000到10 100次迭代中持续优化。

图6 大规模第一组数据在粗调阶段总成本随迭代次数变化曲线

图7 大规模第一组数据在精调阶段总成本随迭代次数变化曲线

5 结 语

将通信网络中服务器部署方案这一实际问题建模为服务器选址问题与费用流问题的整合。本文同时考虑服务器部署选址与服务器档次选择这两个NP难问题的叠加。通过适合大规模组合优化问题的模拟退火算法与适合大规模网络中快速求解费用流的网络单纯形算法结合，求解总成本更低的服务器部署方案。

本文创造性地运用两阶段模拟退火对问题进行求解。服务器部署方案的总费用由服务器硬件成本、部署服务器成本和网络带宽租赁费用组成。在满足消费节点带宽需求的前提下，得出总成本尽可能小的部署方案。通过在90 s的时间内，在两种规模数据上对比模拟退火-网络单纯形算法给出的方案与贪心-Dinic算法给出的方案，本文算法能够减少10%以上的总成本，且随着数据规模的扩大，优势更加明显。

本文探索了引入档次选择的服务设施选址问题，同时两阶段模拟退火的设计也为这一类问题提供了参考解决方案。