基于卷积算法的指标权重模型在配电网建设项目后评价的研究

吴 军 王义贺 薛龙江 刘胜利 李子涵 薛 俊

1(国网浙江平湖市供电有限公司 浙江 平湖 314200)2(东北大学 辽宁 沈阳110819)3(国网辽宁省电力有限公司经济技术研究院 辽宁 沈阳110015)

0 引 言

配电网的稳定运行是保证工业生产和日常生活基本需求的前提条件，因此近年来国家加大了对配电网项目的投资和建设[1]。随着我国各项经济体制和电力体制的变革，配电网建设是否可实现国家投资预期效益已被社会各层所关注[2]。因此本文在上述的大环境下，以配电网自身性质为基础，构建配电网建设项目后评价体系，在评价过程中需采用优化后的权重参数构建指数权重模型，再通过该指数权重模型评价配电网建设项目。

本文研究基于卷积算法的指标权重模型在配电网建设项目后评价，该评价方法通过改进学习率自适应调整方法和改进的学习率退火方法，改进卷积算法的权重参数，实现对配电网建设项目中的多种一级指标和二级指标评价，为配网建设工程相关研究提供参考。

1 配网建设工程后评价模型的构建

1.1 配网工程后评价指标体系

以系统性原则、完备性与相关性原则、可评价的实用性原则、定量和定性相结合的原则以及层次性原则为依据[3]，构建后评价指标体系。配电网建设项目后评价指标体系如图1所示。

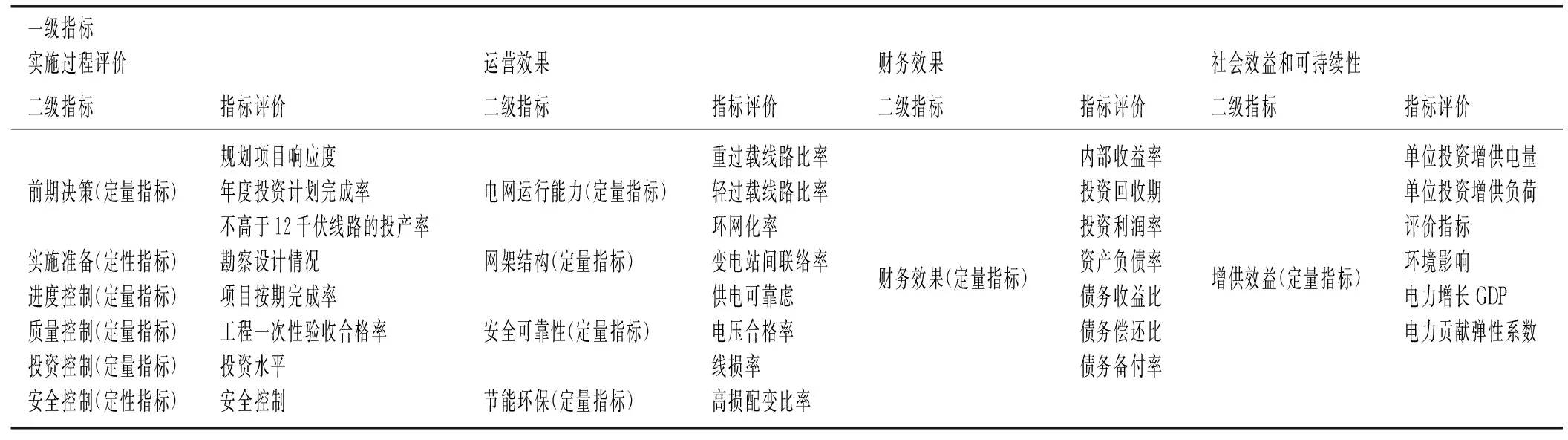
一级指标实施过程评价运营效果财务效果社会效益和可持续性二级指标指标评价二级指标指标评价二级指标指标评价二级指标指标评价前期决策(定量指标)实施准备(定性指标)进度控制(定量指标)质量控制(定量指标)投资控制(定量指标)安全控制(定性指标)规划项目响应度年度投资计划完成率不高于12千伏线路的投产率勘察设计情况项目按期完成率工程一次性验收合格率投资水平安全控制电网运行能力(定量指标)网架结构(定量指标)安全可靠性(定量指标)节能环保(定量指标)重过载线路比率轻过载线路比率环网化率变电站间联络率供电可靠虑电压合格率线损率高损配变比率财务效果(定量指标)内部收益率投资回收期投资利润率资产负债率债务收益比债务偿还比债务备付率增供效益(定量指标)单位投资增供电量单位投资增供负荷评价指标环境影响电力增长GDP电力贡献弹性系数

由图1可知，配网投资项目后评价指标体系中分为一级指标和二级指标，一级指标分为实施过程评价指标、运营效果评价指标、财务效果评价指标、社会效益和可持续性评价指标。其中，实施过程评价指标涵盖了前期决策、实施准备、进度控制、质量控制等二级指标；运营效果评价指标涵盖了电网运行能力指标、网架结构指标、安全可靠性指标等二级指标；社会效益和可持续性评价指标涵盖的二级指标为增供效益指标。

1.2 改进的寻优权重参数优化算法

近年来研究人员对卷积神经网络进行了大量的研究，在研究中不断地深化卷积神经网络的复杂度，因此对卷积神经网络的权重参数的要求越发严格[4-5]。为迎合这一现状，以提高权重参数的寻优速度和寻优能力为目标，利用改进的学习率自适应调整方法和改进的学习率退火方法，实现基于卷积的寻优权重参数优化算法的改进。

假设δ为卷积神经网络的参数，要获取配电网工程后评价指标体系中的最优参数，需要计算损失函数值的最小值，假设有e个输入值，同时对应的有e个输出值，则输入值和输出值的对应关系可表达为{(x(e)，y(e))；e∈[1,2,…,E]}，则xe、ye、o(e)分别代表第e个输入值、相对应的标签、卷积神经网络的最后输出，则卷积神经网络的损失值可表达为：

(1)

卷积神经网络通过损失函数值的最小值，获取配电网工程后评价指标体系中最优参数解[6]。

1.2.1改进的学习率自适应调整方法

适应性矩估计(adaptive moment estimation，Adam)是一种可以替代传统随机梯度下降过程的一阶优化算法，它能基于训练数据迭代地更新神经网络权重。改进的学习率自适应调整方法，是在Adam算法基础上的改进，其主要原理为：在算法迭代时会损失函数值，损失函数值差异性可反馈权重参数寻优信息，损失函数值差异性很大时，权重参数寻优过程不稳定，此时降低学习率可改善这种不稳定现象，此过程也叫退火；当损失函数值差异性很小时，通过提高学习率促进权重参数寻优过程稳定性[7]。将上述原理与Adam算法相结合，提高权重参数寻优速度和寻优能力[8]。算法原理为：可从自适应调整学习率中获取损失函数相对变化率，通过量化相对变化率确认每次迭代损失函数值的相对变化，并采用指数滑动平均法对每次迭代损失函数值的相对变化进行平滑处理。算法的基本步骤如下：

(1) 假设当迭代次数为s-1和s-2时相对应的损失函数值为ps-1和ps-2，损失函数的相对变化率公式可表示为：

(2)

损失函数的相对变化率bs是一个整数，可以准确表达损失函数值的增大或减小程度[9]。

(2) 对每次迭代损失函数值的相对变化进行平滑处理，平滑处理公式可表达为：

(3)

因为每一个损失函数值都是在不同样本基础上获取，因此损失函数值并不完全一致[10]。为了平滑处理的效果更好，令β为平滑参数，其取值无限趋近于1。

(3) 假设一个学习率为α，则cs便是α的分母项，代入到Adam算法中，获取迭代次数，迭代公式可表示为：

s←cs+1

(4)

qs←Δθ(s-1)

(5)

ns←β1ns-1+(1-β1)qs

(6)

(7)

(8)

(9)

(10)

当训练权重系数样本初期，损失函数值的变化幅度不大，此时平滑处理值cs也不大，当取值很小时，会导致迭代步长突然上升[11]，由于适当的迭代步长ΔθS可促进算法的迭代性能，因此当迭代步长突然上升时，会使权重参数寻优过程不平稳，因此需对平滑处理值cs执行固定设置。传统的设置平滑处理值方法通常为人为设置，导致整体设置过程烦琐，且精准度不高[12]。为避免这些问题，采用阈值设定法设定平滑处理值，该设定方法不仅设定过程简便易操作，而且适合任何卷积神经网络模型。设定起始步长为0，终止步长为0.09，训练轮数为5，批大小ε=134，设步长上限为0.08。确定步长上限后，反推平滑处理值cs的下限，当θ=0时，改进权重优化算法的迭代步长公式表达为：

(11)

在上述迭代反推平滑处理值的过程中,平滑处理cs的下限公式可表达为：

(12)

1.2.2改进的学习率退火方法

设置一个训练集为D，f(x；D)是在训练集D上的模型f在x上的预测输出，E表示期望输入值,则该模型的期望预测值公式可表示为：

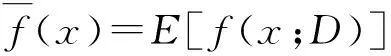
(13)

由于样本是分批采集的，因此不同的样本会产生方差，该方差值可表示为：

(14)

噪声值公式可表示为：

ε2=E(yD-y)2

(15)

式中：yD表示期望输出值。而期望预测值与标记值y会存在一定的差值，该差值的公式可表达为：

(16)

为了提高权重系数的寻优速度和寻优性能，需要将学习率提高后降低，或是降低后再提高[13]，该退火过程作为权重参数优化算法的一部分，在模型训练的末期发挥着重要作用。学习率退火公式为：

(17)

式中：1+γs表示退火上限。

1.3 模糊综合后评价模型的建立

后评价模型利用改进后的权重参数将评价指标的数据形式通过统一的方式体现配电网建设项目的总体效果，将模糊综合评价与配电网建设项目的后评价工作相结合，实现模糊综合评价。该模糊综合评价不仅可以确定后评价的总体目标，还可将评价指标按照层次化标准划分，构建一个层次化模型对配电网建设项目进行评价，评价时会存在很多主观因素[14]，需要将模糊数学与配电网建设项目后评价工作相结合，得到更加客观的评价结果。可以通过调研的方法将各位研究人员对配电网建设项目的评价收集起来，对评价进行定量综合分析，由于各个评价因素对配电网建设项目的重要程度(隶属度)都不一样，因此要结合配电网建设项目的隶属度完成评价。以下为模糊综合模型的构建流程：

(1) 分别构建评价一级指标集合和二级指标集合：

H={H1,H2,H3,H4}，Hi={Hi1,Hi2,…,Hij}

(18)

式中：Hij是第i个准则层中的第j个指标。

(2) 以安全质量为评价目的构建评语集为：

R={R1,R2,R3,R4}={优，良，中，差}

(19)

(3) 分别确定一级指标和二级指标的权重集为：

(20)

(4) 构建评价隶属矩阵W为：

(21)

Wij表示第i个评价因素对第j个评价等级的隶属度，评语集中评价等级个数用n表示，被评价因素的个数用m表示。

(5) 二级模糊综合评价。先完成一级模糊综合评价，并通过层次分析获取指标权重和评价隶属度矩阵W，以模糊运算法则为基础，经过运算后进行归一化，获取评价因素对评价集的隶属度向量S。然后开始二级模糊综合评价，获取总的评价向量B，并得到综合评价结论，可用公式表达为：

B=W·Sαs

(22)

为了在配电网建设项目中的后评价更加直观[15]，需将综合评价结果转化为数据分值，评价等级分值用R表示，评价结果公式可表达为：

Q=B·R

(23)

至此，评价模型构建完成，如图2所示。

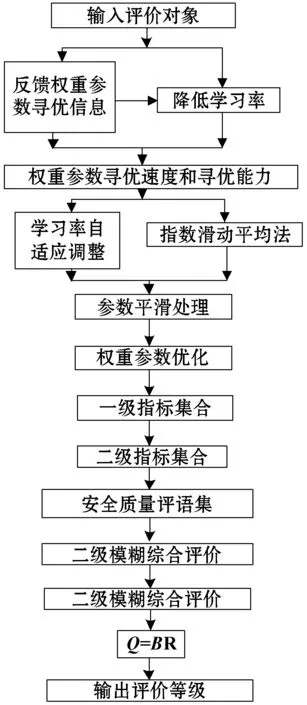
图2 模糊综合模型

2 实验分析

为了验证配电网建设项目后评价的准确率、稳定性，实验分析本文方法对杭州市配电网建设项目实施过程后评价和运营效果后评价，验证本文方法的评价效果，同时统计分析了本文方法的评价性能。

2.1 实施过程后评价

2.1.1投资变化率评价

设定杭州市为研究区域，将杭州市划分为1区、2区、3区和4区，则该市在2018年配电网建设项目的投资情况如表1所示。

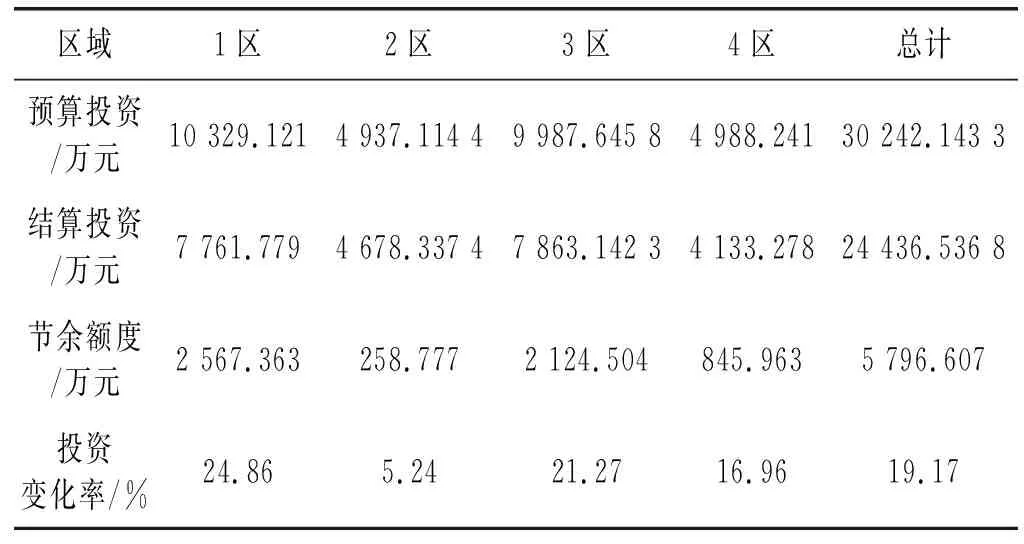
表1 2016年杭州市配电网项目建设投资变化情况

由表1可知，本文方法评价得出：4个区域结算投资均小于预算投资，说明结算工程的总投资在工程总预算之内，造价水平同时也得到有效的控制。4个区域都存在投资变化率，但1区、3区和4区的投资变化率比2区高40%～70%，因此需综合分析导致1区、3区和4区投资变化的原因：(1) 在配电网项目的实际建设过程中，会产生设计或方案的变化。此时，相对应的建设工序也会产生变化，原有的安装程序可能在设计方案变化后被剔除，因此安装费用也相应地降低，由此造成投资变化率加大。(2) 配电网项目建设前，建筑材料价格突然降低，或是在建设过程中实际用料量低于预计用料量等现象都会造成投资变化率加大。

2.1.2年度投资计划完成率评价

年度投资计划完成率=年度投资完成数量/年度安排投资数量。表2为年度投资完成情况表。

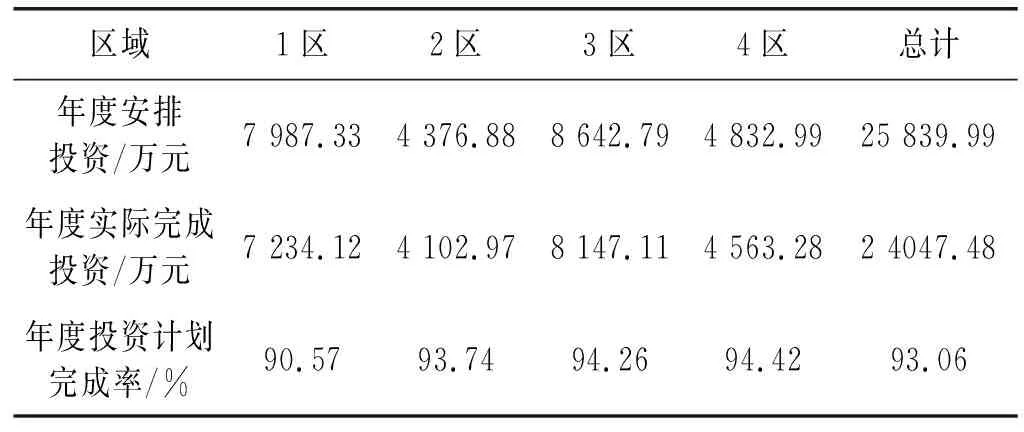
表2 2018年投资完成情况

由表2可知，本文方法评价得出：杭州市4个区2016年年度安排投资总额度为25 839.99万元，年度实际完成投资额度为24 047.48万元，年度投资计划完成率为93.06%，且1区、2区、3区和4区年度投资计划完成率分别高达90.57%、93.74%、94.26%、94.42%，完成情况很好。促进年度投资完成率较高的原因可能是配电网项目建设过程中价控措施效果显著、年度规划较为合理、工程的实施过程严格监控等。

2.2 运营效果后评价

2.2.1变电站间联络率评价

配电网中存在多个变电站，多个变电站存在互相联络的现象，这种变电站间的联络率能够反映变电站间的联络能力，也是反映电源断电后的负荷转移能力的指标之一，变电站在联络过程中会存在很多条联络线路，当电源断电后负荷转移能力与供电影响范围成反比，负荷转移能力越高，供电影响范围越小，配电网稳态效果越好。表3为2017年-2018年变电站间联络率情况表。

表3 2017年-2018年变电站间联络率情况(%)

依据表3绘制2017年、2018年杭州市4个区变电站间的联络率矩形图，如图3所示。

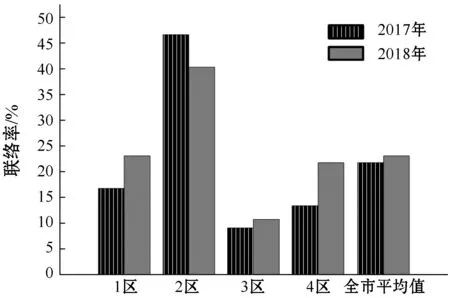
图3 2017年-2018年杭州市4个区变电站间的联络率

综合分析表3和图3可知，本文方法评价得出：2017年-2018年杭州市变电站间的联络率整体呈现上升趋势，但在杭州市的2区域，2018年的变电站间联络率要低于2017年变电站间的联络率。经过分析，造成这一现象的主要原因为：2017年时变电站间的联络线路主要通过QA线与华前线和HA线相连接实现，但从2018年开始，完成了QAI线网架工作完善工作后，QA线不再与之前的华前线和HA线连接，而是改为与QD线连接。由于中间省去了站间联络，因此原来为了站间联络设置的DP场线也被停用，站间联络结构缩减，使线路互供能力提高，当线路故障发生时可通过其他途径延续线路工作，因此电网运行更加稳定安全。

2.2.2综合电压合格率评价

电压在可产生偏差区域内会产生波动，该波动概率可通过综合电压合格率直观地反馈，电压合格率不仅可查验电能质量以及电压合格率控制目标完成情况，还可反映配电网稳定性。表4为2017年-2018年4个区的综合电压合格率统计数据。

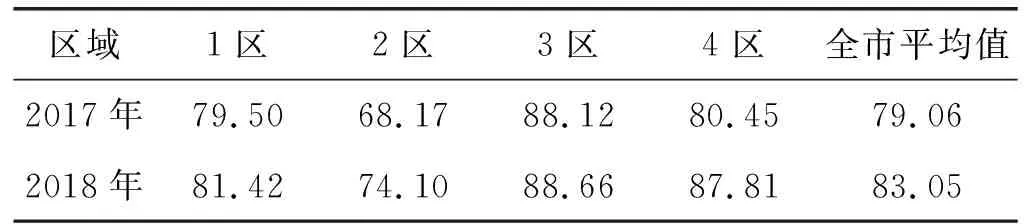
表4 2017年-2018年4个区的综合电压合格率统计数据(%)

表4可知，本文方法评价得出：经过2017年配电网项目的建设，在2018年时杭州4个区域的综合电压合格率分别达到81.42%、74.10%、88.66%、87.81%，相较于2017年，均有所提高，但整体的综合电压合格率仍然有可上升的空间。依据表5中的数据绘制2017年-2018年4个区的综合电压合格率统计数据图，如图4所示。

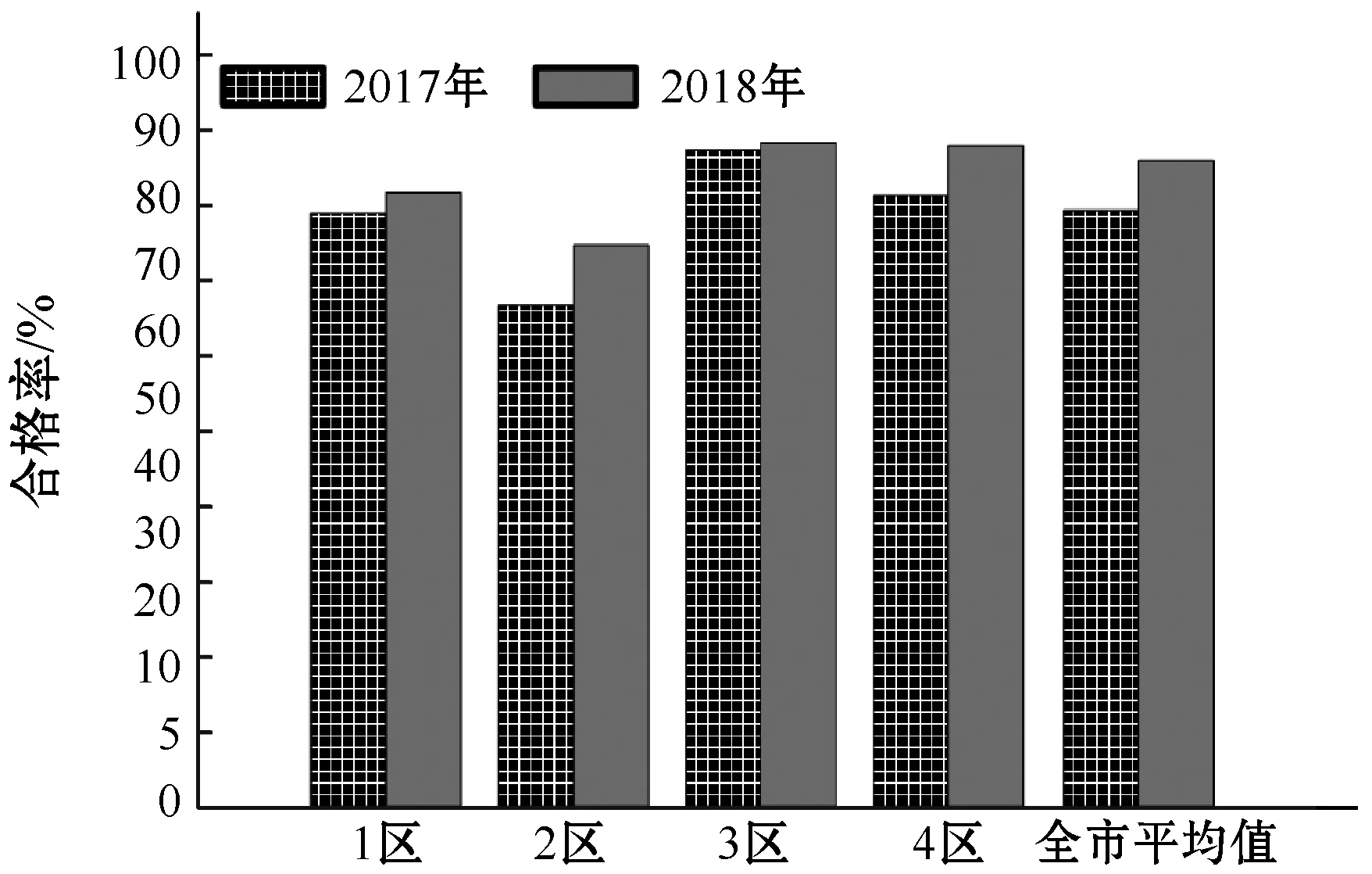
图4 2017年-2018年4个区的综合电压合格率统计数据

图4可直观呈现出本文方法评价结果为：2018年4个区的综合电压合格率均高于2017年，但1区和2区的整体综合电压合格率比另外两个区要低。经分析造成这种现象的主要原因为：供电路线太长、经过长时间使用线路磨损导致电压偏低等。

2.3 评价性能分析

为了验证本文方法的性能，需对其变化曲线进行分析，如图5为本文方法、灰色综合评价方法以及改进可拓物元模型评价方法在测试集上的性能变化趋势，灰色综合评估法是一种专家评判的综合性评估为基础，以灰色关联分析理论为指导的评估方法，而改进可拓物元模型主要为改进关联函数，这是一种新的关联函数，是通过关联函数中的分段函数对评价指标进行物元分析。

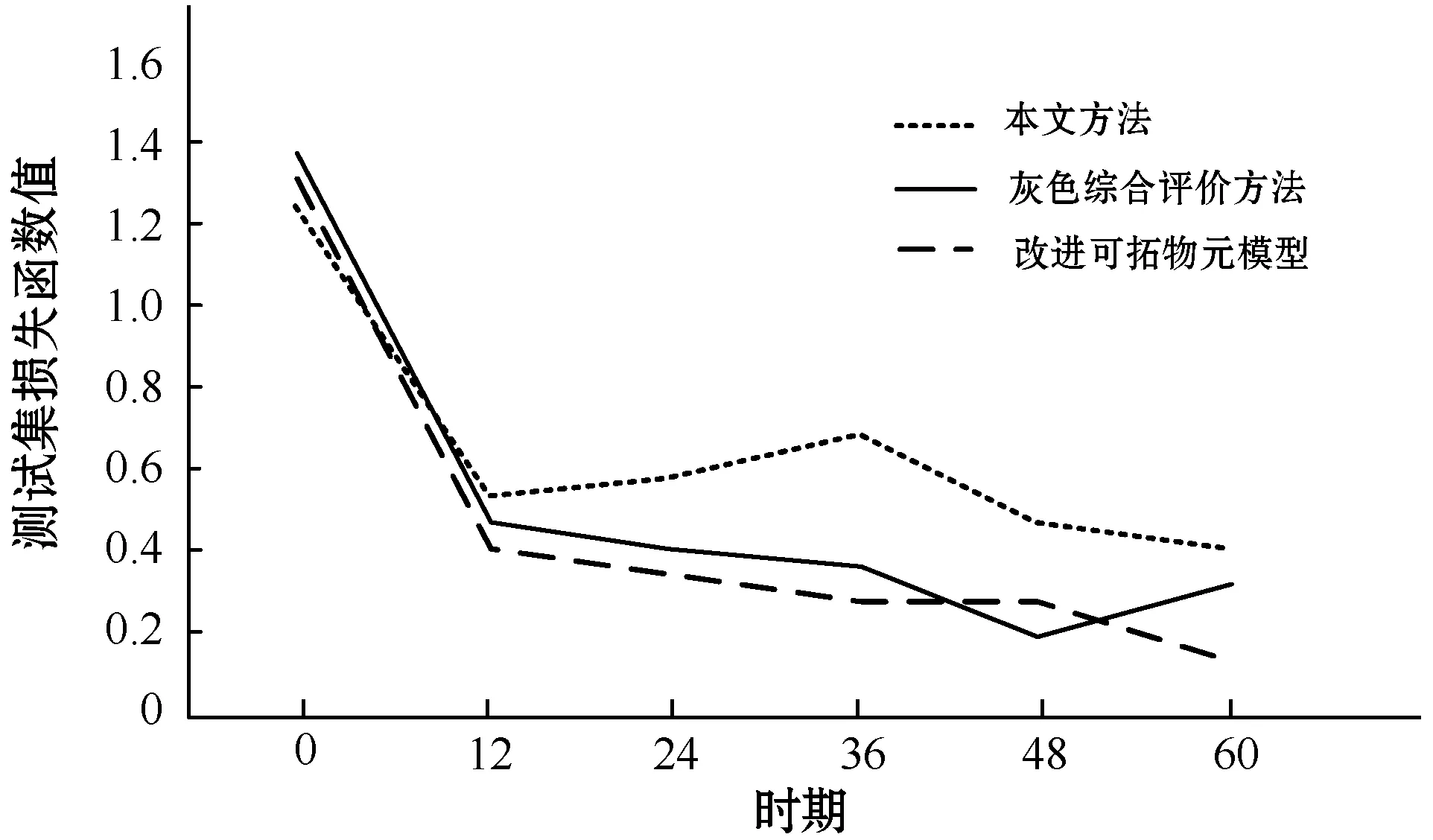
(a) 损失函数值变化曲线

由图5(a)可知，相较于灰色综合评价方法，本文方法在测试集中的损失函数值更小，但在0时期到12时期的损失函数值差距较大，当损失函数值差距越大，越可促进权重参数寻优过程的平稳进行，本文方法的性能就越好。由图5(b)可知，本文方法的测试集准确率要高于灰色综合评价方法以及改进可拓物元模型评价方法，因此本文方法对配电网建设项目后评价的准确率很高。

由于普通的配电网建设项目后评价方法会随着参数的变化而产生准确率方面的差异，为了验证本文方法的稳定性，设置不同的学习率，验证本文方法在不同的学习率条件下评价准确率变化情况，如图6所示。

由图6可知，当设置不同参数时，本文方法在每个周期的准确率变化幅度很小，甚至可忽略，因此说明虽然设置了不同的参数，但本文方法在参数的变化时依然可保持高准确率稳定评价，由此可知，本文方法在性能方面具有很高优势。

3 结 语

本文根据配网建设工程的特性构建综合后评价指标体系，基于卷积算法优化确定权重参数，构建配电网建设工程的综合后评价模型，以实施过程、运营效果、财务效果以及社会效益和可持续性为一级指标，对配网建设工程展开项目后评价工作，并以杭州市2018年配网建设工程为实际案例，对其进行了项目后评价分析。实验表明，本文研究的基于卷积算法的指标权重模型在配电网建设项目后评价方法可良好评价配电网建设实施过程和运营效果等项目，即使指标体系中的权重参数发生变化，本文方法评价结果的准确率也不会产生变化，可稳定评价配电网建设项目，为配电网以后的建设发挥重要作用。