基于差分隐私的健康医疗数据保护方案
2022-09-07白伍彤陈兰香
白伍彤 陈兰香
(福建师范大学数学与信息学院 福建 福州 350117)(福建省网络安全与密码技术重点实验室 福建 福州 350117)
0 引 言
国务院办公厅于2016年6月颁发的《关于促进和规范健康医疗大数据应用发展的指导意见》(下简称为《意见》)指出国家重要的基础性战略资源是健康医疗大数据,健康医疗大数据相关应用的发展将为健康医疗模式带来深刻改变,为健康医疗大数据的发展定下基调。
2016年10月,中共中央、国务院印发了《“健康中国2030”规划纲要》,提出要加强并推进基于区域人口健康信息的医疗大数据开放挖掘和各类应用体系的建设。《意见》中指出,针对法律法规和隐私安全问题,要求完善数据开放共享支撑服务体系,针对健康医疗数据安全体系加快建设,同时对于人口健康医疗信息的工程技术、内容安全等多方面进行规划制定以确保各类关键信息以及核心系统的安全可控与稳定[1]。
从隐私保护的角度来说,隐私的主体是单个用户,只有涉及到某个特定用户的敏感信息才叫隐私,如果是发布群体用户的信息(一般叫聚集信息)不算泄露隐私。因此,充分利用并挖掘大数据的价值可以不需要涉及到任何用户的个人隐私。
在健康医疗大数据领域即是如此,利用这些大数据对于优化资源配置、提供临床决策与精准医学研究等方面具有重要的价值,但怎样合理合法地利用这些数据的同时又能保障用户的隐私信息,是当前亟待解决的问题。
针对传统隐私保护模型存在的问题,本文提出利用基于Laplace机制与指数机制的差分隐私保护方法,对健康医疗数据中的数值型与非数值型数据提供高强度的隐私保护。通过大量的实验分析,针对差分隐私保护参数ε对数据的可用性与隐私保护水平两者的平衡进行评估,得到不同类型的健康医疗数据的适当的参数取值。
1 相关工作
早在20世纪80年代初,Cox[2]首次提出了匿名化的概念,并指出这种方法可应用于隐私信息的保护。Sweeney[3]提出k-匿名(k-anonymity)模型的数据匿名化隐私保护方法,考虑的是数据拥有者想与其他用户共享其私有数据,但是不能泄露他的身份的应用场景。针对这个问题,他们通过泛化与分解等方式对原始私有数据进行匿名化处理,有效地解决了隐私保护的问题。k-匿名模型的核心思想是:所发布的数据中任意一条记录(也称之为一个等价类)都被要求与另外的至少k-1条记录是不可区分的,则称该系统提供k-匿名保护。在k-匿名处理后的数据被攻击者获得的同时会至少得到不同的k个记录数据,这样便使得攻击者即使通过攻击得到了数据,但其也无法做出相应的准确判断。该匿名模型中隐私保护的强度被表示为参数k,随着k值的增大,隐私保护的强度也随之增强,但因此会使得更多的信息丢失,数据的可用性也会越来越低。
Machanavajjhala等[4]在研究中发现了k-匿名模型中存在着对于敏感属性未进行有效制约的不足,因此攻击者就可以通过背景知识攻击以及一致性攻击等多种不同方法来推断出数据中的敏感信息与某个人之间的关系来得到攻击者所关心的个人隐私数据,这导致了数据记录中的个人隐私信息发生泄露。例如攻击者使用一致性攻击时,当一个攻击者获得了k-匿名化数据,当被攻击者所处的记录中都是患有某一类传染疾病的病人,那么攻击者很轻易做出被攻击者是确定患有此类传染疾病的判断。那么为了防止这种一致性攻击,Machanavajjhala等对于k-匿名模型进行改进,提出了新的隐私保护模型:l-多样性(l-diversity),它保证了任意一个等价类中的敏感属性都至少有l个内容不同的值,一定程度上避免了敏感属性所取值单一的情形。
针对l-多样性模型在一些特殊情况下不适用的问题,Li等[5]提出了t-近邻(t-closeness)模型,它对准标识符属性与敏感信息的全局分布之间的联系进行了约束限定,将特定敏感信息与半标识列属性之间的联系减弱了,这样便使得对敏感信息的分布信息进行属性泄露攻击的可能性有所减少,但同时也会使得信息有一定程度的丢失。
所有匿名机制试图尽量减少信息丢失,然而这种尝试却为攻击提供了漏洞,Wong等[6]称之为“最小性”攻击,他们提出的m-机密性(m-confidentiality)模型可以在较小的开销和信息丢失情况下抵制此类攻击。
然而k-匿名模型及其改进方法存在两个主要的缺陷:(1) 这些模型总是因为新型攻击方法的出现而需要不断改进,从而陷入一个无休止的循环中;(2) 该类型的模型对攻击者的攻击模型和背景知识给出了过多的些许在现实中不完全成立的假设,所以攻击者是可以找到多种不同的攻击方法进行攻击以达到其窃取隐私信息的目的。其根本原因是对于其隐私保护的水平无法通过严格有效的方法得到证明,同时无法定量地分析其隐私保护水平。
因此,找到一种鲁棒性更好的新的隐私保护模型,使得它能够在攻击者所掌握最大背景知识的条件下抵御不同形式的攻击就是研究者需要解决的问题。差分隐私保护模型就是在这样的需求下提出的。
差分隐私(Differential Privacy,DP)在2006年时被微软研究院的Dwork[7]提出,这是一种新的隐私保护模型。此方法定义了一个严格的隐私保护模型,在数据中加入干扰噪声来保护数据中的用户隐私。如此,即便假设攻击者已经获得了最大背景知识的攻击条件之下,也无法获得记录的隐私信息数据;同时对隐私保护水平给出了严格的数学证明和量化评估方法,给出了一个数学描述来测量一个扰动机制究竟能够带来多大程度上的保密性。这解决了传统隐私保护模型中的一些缺陷。此后,还给出了差分隐私保护模型的综述[8]。
因差分隐私保护模型相较于其他模型的诸多优势,使其引起了计算机科学、密码学等诸多领域的关注和研究,成为了当前隐私保护的研究热点,也迅速地取代了一些传统的隐私保护模型。
差分隐私保护基于数据失真技术将某种特定分布的随机噪声添加进需要处理的数据集中,进而得到被扰动后的新的数据集来达到对数据隐私保护的目的。因为数据集的大小对所加入的噪声强度不影响,噪声量只与全局敏感度相关,因此即便是大型的数据集,使用差分隐私也只需通过添加较为少量的噪声干扰就可以使数据集得到很好的隐私保护。差分隐私中常用的两种机制有拉普拉斯Laplace机制[9]和指数exponential机制[10]。
文献[11]将差分隐私模型相比于传统隐私模型的优势进行了分析,并针对差分隐私的基础理论和差分隐私在数据分享等应用的研究进行了综述。文献[12-13]对差分隐私在数据发布与数据分析两个领域的应用进行了综述。文献[14]介绍了本地化差分隐私的原理与特性,并对本地化差分隐私保护技术进行综述。文献[15-16]对差分隐私的基础理论和目前的研究进展进行了综述。
传统隐私保护模型以及差分隐私保护模型的研究成果丰硕,但是在健康医疗领域,关于隐私保护的有效方案还比较缺乏。特别地,具有量化特征以及强隐私保护特点的差分隐私保护机制也存在一个弱点:由于对于背景知识的假设很强,需要在数据的查询结果中添加进大量的随机数据,这使得数据的可用性大大降低。为了在数据隐私保护强度与可用性之间取得平衡,本文对差分隐私保护参数ε对数据隐私保护强度与可用性的影响进行评估,通过实验分析给出不同类型的健康医疗数据的适当的ε取值。
2 预备知识
2.1 符号定义
本文使用的符号定义如表1所示。

表1 符号说明
2.2 差分隐私保护
对于一个随机算法S,PS为S所有可能输出的集合,对于任意的两个相邻数据集D和D′及PS的任意子集AS,满足:
Pr[S(D)∈AS]≤exp(ε)Pr[M(D′)∈AS]
(1)
则称算法S满足ε-差分隐私。在这个定义中,当某个数据记录发生变化时,数据库的统计分析结果对于此变化是不敏感的,意味着在数据集中单条记录的存在与否对计算结果的影响可忽略不计,所以攻击者无法通过向数据库递交多次查询后根据返回结果而获取个体隐私信息。
差分隐私算法针对不同的数据类型可以使用不同的实现机制,在最常用的两种机制中Laplace机制常用于记录中数值型数据的隐私保护,指数机制则常用于对非数值型数据进行处理。
2.2.1Laplace机制
Laplace机制是将服从Laplace分布的噪声数据添加在输出结果上,使得原始数据发生一定的扰动,使得接收者无法分辨在两个相邻的数据集D和D′上所产生的输出结果的差异,其定义如下。
给定函数f:D→Rd,若算法S的输出满足式(2),则称S满足ε-差分隐私。
(2)
(3)
Laplace机制的概率密度函数如图1所示,在不同参数的Laplace分布中,隐私保护参数ε越小,隐私保护水平越高,数据的可用性就越低。当ε=0时,算法S输出的结果则不能反映出有关数据集的任何有用信息。
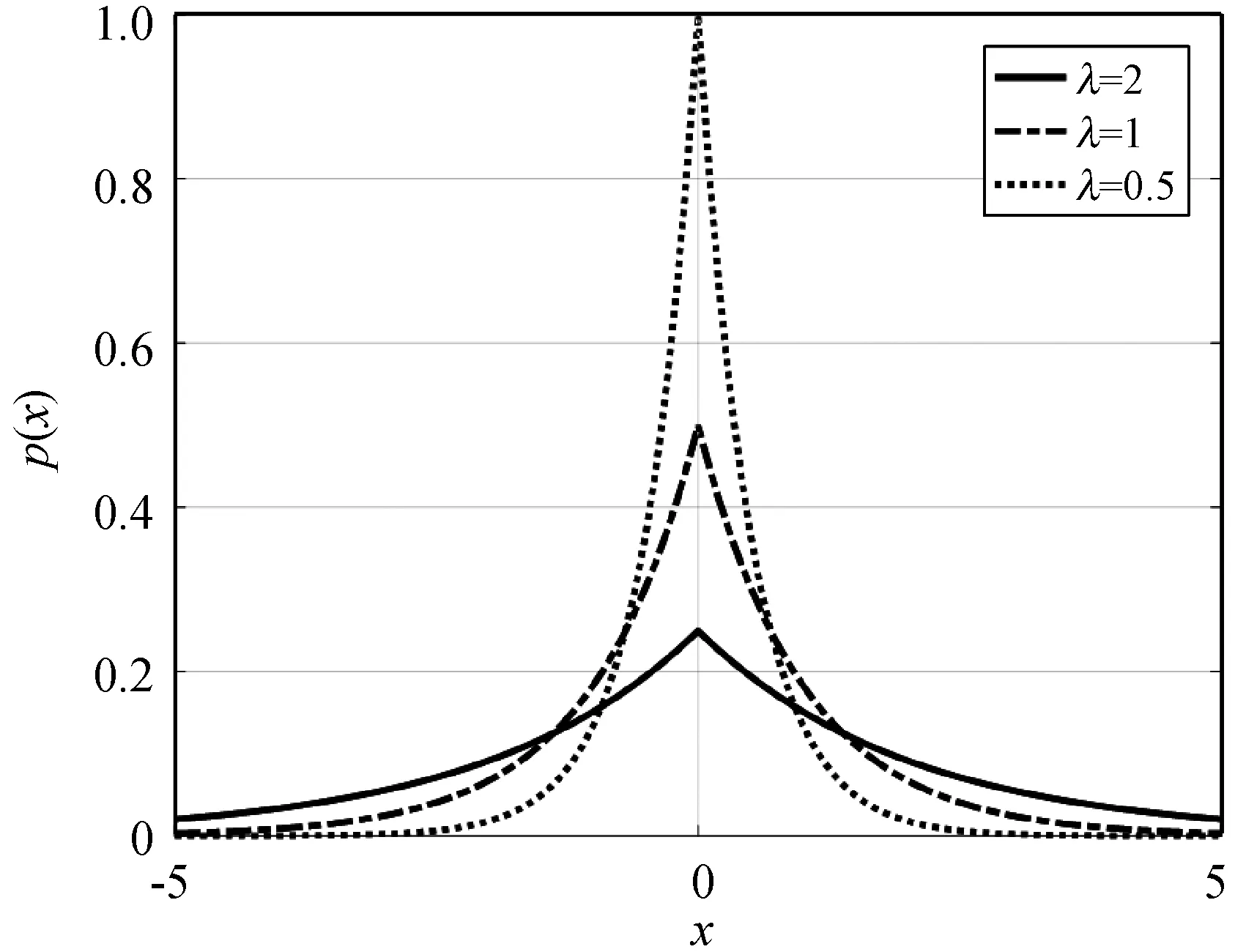
图1 Laplace机制的概率密度函数
2.2.2指数机制
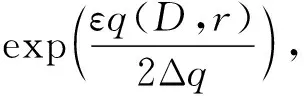
(4)
指数机制中参数q对于单个记录的敏感性低,其函数敏感性公式如式(5)所示。
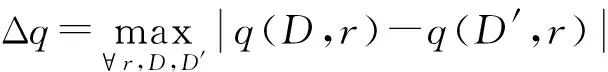
(5)
3 基于差分隐私的健康医疗数据保护
3.1 基于差分隐私的数据处理框架
针对健康医疗数据的高敏感性特征,根据数据类型对数据加入不同类型的噪声对数据进行一定程度的扰动。但是在加入噪声过程中要平衡数据的可用性与安全性,使得发布后的数据在依然保留整体统计信息可用性的前提下保护单个用户的隐私信息。本文提出的基于差分隐私保护的健康医疗数据保护方案的数据处理框架如图2所示。
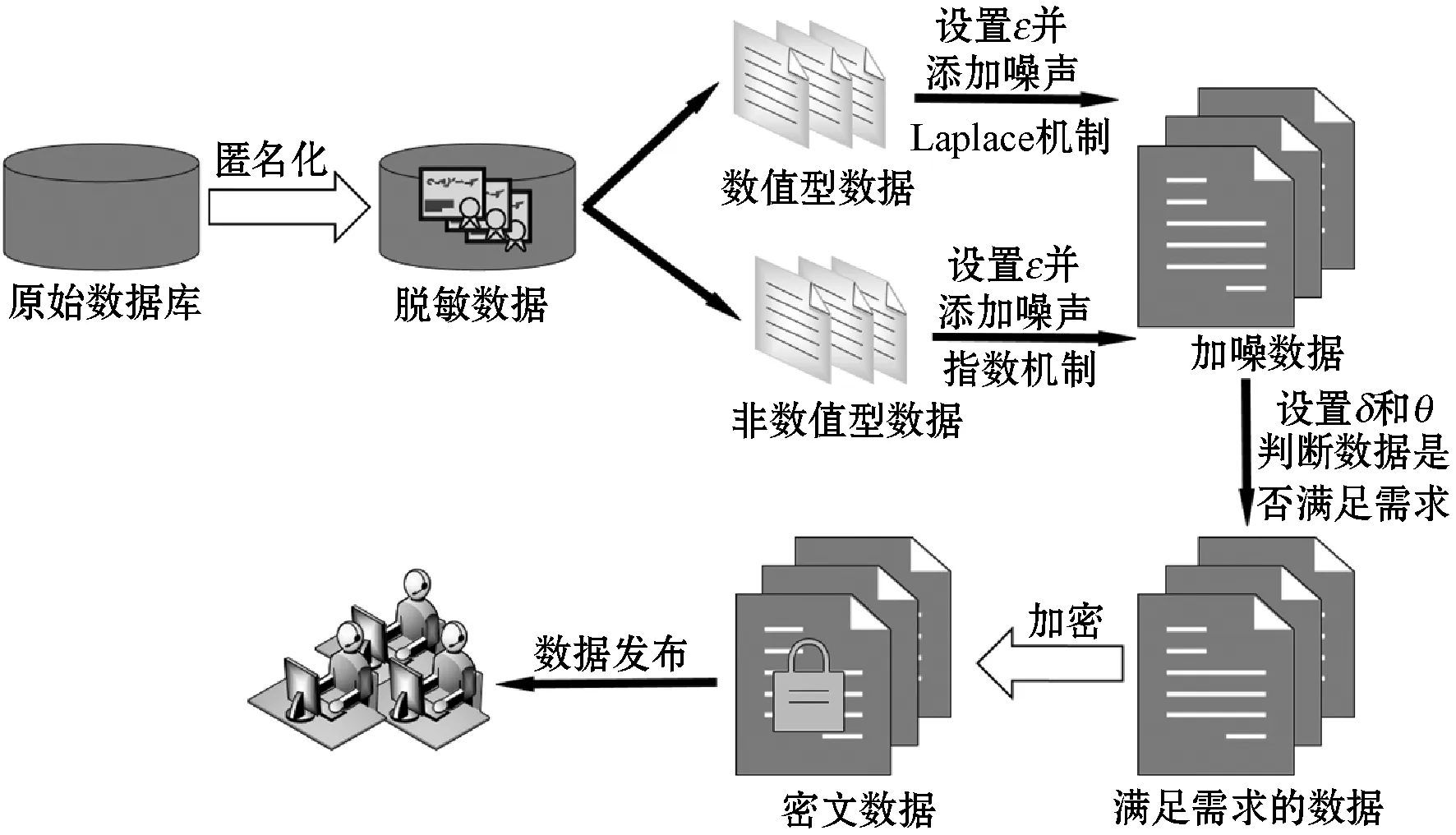
图2 基于差分隐私的数据处理框架
首先将健康医疗数据库中直接关联个体用户的敏感内容,如姓名、身份证号及电话等个体标识信息去除。然后将数据分为数值型与非数值型数据两类,数值型数据采用Laplace机制,非数值型数据则采用指数机制,分别对数据添加噪声。为了同时保证数据的可用性和安全性,进一步平衡设置了误差参数δ和满足误差的统计个数θ,通过控制δ和θ的取值来满足在不同数据集上对可用性和安全性的不同需求。为了保护数据的机密性,数据以加密形式存储,当数据发布给使用者时,使用者根据授权解密数据,然后对加了噪声的数据进行分析处理。
在使用Laplace机制和指数机制时,需要根据数据的用途设置隐私保护参数ε以平衡数据可用性和隐私保护程度。
3.2 方案详细设计
为了对健康医疗数据的隐私保护强度与可用性进行评估,我们对数值型与非数值型两类健康医疗数据设计了Laplace机制与指数机制分别对数据进行基于差分隐私的保护,按对不同数据的安全性和可用性需求进一步设定误差参数δ(即处理前后统计数之差与原数据比值)和满足误差的统计个数θ,同时引入皮尔逊相关系数来进一步判定数据在处理前后的相似度来保障处理后数据的可用性(0.8~1.0极强相关)。我们以身体质量指数(Body Mass Index,BMI)和年龄作为数值型数据的案例,对其应用Laplace机制添加噪声;而非数值型数据则以性别为例,对其应用指数机制加入噪声,然后将处理后的数据加密后发布,使数据使用者得到数据后解密再进行相关的数据统计分析。
在针对不同类型的数据使用差分隐私处理时,因为差分隐私的定义表明对于隐私保护参数ε的取值与对原始数据的扰动影响程度成反比,即对隐私保护参数的取值越小,加入原始数据的噪声量越大,对于原始数据的扰动也就越大。对于健康医疗数据而言,要求数据在用于数据分析时的统计结果波动不大的同时使数据的隐私得到保护,即数据的可用性和安全性都有保障,因而对于隐私保护参数ε数值的设置就需要根据数据的不同来进行调整以达到较好的效果。
针对数值型数据的Laplace机制的处理算法如算法1所示,因为算法采用Python语言实现,因此其算法的伪代码中有Python中的常用函数,其中np是Python的一个运算函数库,random()表示生成随机数函数,按所设置的Δf和ε随机生成噪声,将噪声添加在原始数据中得到加噪数据,同时判断经过噪声处理后的数据是否满足了δ和θ预先设定的要求。
算法1Laplace机制扰动算法
输入:数据库中的数值域age,BMI,ε,δ和θ。
输出:加入噪声的age_d和BMI_d。
2)u1=np.random.random(),
u2=np.random.random()
//生成取值范围为[0,1)的随机浮点数u1和u2
3) ifu1≤0.5
noise_value=-λ*np.log(1-u2)
else
noise_value=λ*np.log(u2)
4)age_d=age+noise_value1;(ε=ε1)
BMI_d=BMI+noise_value2;(ε=ε2)
5) pearson(age,age_d)
pearson(BMI,BMI_d)
6)θ1=0
ifδ1>δandδ2>δ
数据处理误差不符合要求
else
θ1=θ1+1
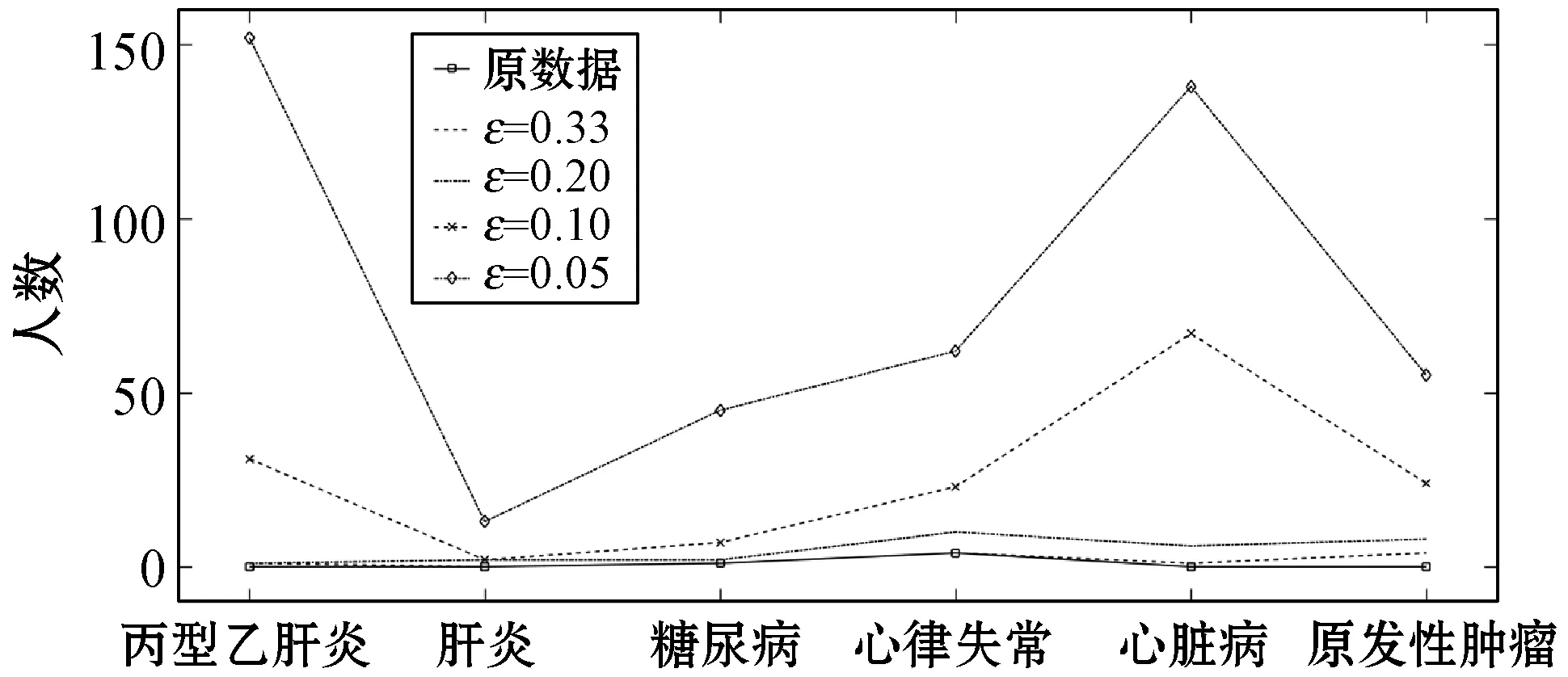
ifθ1≥θand 0.8 处理前后数据相似度很高且数据处理满足要求 else 数据处理未满足要求 ε=ε+0.01 Laplace() 针对非数值型数据的指数机制的处理算法如算法2所示,健康医疗数据中非数值型域比较多,在这里以个体性别为例。算法中round()表示取指定位数的小数,random_pick()表示以指定概率从列表中取值。通过δ和θ的判断来检验处理后的数据能否达到处理要求。 算法2指数机制扰动算法 输入:数据库中的非数值域gender,ε,δ,θ。 输出:加入噪声的gender_d。 1) setsum=0,Δq,ε 3)exponents_list: exponents_list.append(math.exp(expo)) //将各项对应的expo存入exponents_list 4)sum=exponents_list[0]+exponents_list[1] foriinexponents_list 5)some_list=[′female′,′male′] disease_list=dict[disease] 6)gender_d=random_pick(some_list,disease_list) 7) pearson(age,age_d) pearson(BMI,BMI_d) 8)θ1=0 ifδ3>δ 数据处理误差不符合要求 else θ1=θ1+1 ifθ1≥θand 0.8 处理前后数据相似度很高且数据处理满足要求 else 数据处理未满足要求 ε=ε+0.01 Exponential() 对数据进行加噪处理后,再利用常用对称加密算法,比如AES对加噪数据加密,密文数据就可以发布。而用户要想利用这些发布的数据,仍然要从数据持有者得到授权才可以得到密文数据并解密数据进行分析,对密文数据的授权不是本文的研究重点,利用已有的数据授权方法即可。 实验部分我们在64位Windows 10操作系统个人电脑上使用MATLAB R2016b软件进行了数值模拟,个人电脑具有16 GB的随机存取存储器(RAM)和2.20 GHz的Intel Core i7- 6650U CPU。数据为存储在MySQL数据库中的11 640条健康医疗数据记录(数据集来源: (1) https://archive.ics.uci.edu/ml/index.php; (2) https://github.com/susanli2016/Machine-Learning-with-Python数据量为4 019条)。同时根据不同的数据我们测试了不同的隐私保护参数ε取值对于数据安全性和可用性的差别。在实验中为能够细致地保障数据处理后可用性和安全性,将隐私保护参数ε的变化幅度分别进行设置。因非数值型分组只有男性和女性两种,组中数据量相较于数值型较多,在ε数值较小时统计后的数据差异较小,因此将对非数值型数据隐私保护参数变化幅度设置为0.001(指数机制),在数值型数据分组中,因分组较多,每个分组中的部分数据量会较小,在参数ε设置较小的情况下会出现数据波动很大而导致数据可用性不高,所以将数值型数据的隐私保护参数变化幅度设置为0.01(Laplace机制)。实验中ε的初始值设定为中间量0.5,依次根据调整幅度进行测试以找到安全性与可用性的一个平衡。再根据进行实验的数据分析将实验中误差参数δ设为20%,数值型和非数值型数据根据不同区间划分后的统计个数分别为30、12,因分组后部分组内数据较少,在进行数据处理时数据波动情况相较于其他分组较大,故而将满足误差的统计个数θ分别设置为20、10以保证数据的可用性较好。数据发布者可以根据对于不同数据的不同需求对ε、δ、θ进行设定和处理来达到对于不同数据使用者的数据隐私保护通用性。 根据性别分类在ε=0.005, 0.004, 0.003与0.002时的加噪前后的疾病统计分布如图3表示。分别在性别为男与女情况下采用不同ε时的数据加噪前后的疾病统计分布,经过多次实验测试发现与年龄数据处理不同的是当ε=0.005时,我们得到的扰动后的数据统计结果与原始数据的统计结果十分相近,而当ε=0.002时,其统计结果误差非常大。 (a) 男性 (b) 女性图3 按性别在不同ε取值下加噪前后的疾病统计分布 根据BMI数据在ε=0.36, 0.3, 0.2与0.1时的加噪前后的疾病统计分布如图4所示,分别统计在BMI<18.5,BMI取值为18.5~23.9、24.0~26.9、27.0~29.9,以及BMI≥30的不同条件下数据加噪前后的疾病统计分析结果分布。 (a) BMI小于18.5 (b) BMI介于18.5~23.9 (c) BMI介于24.0~26.9 (d) BMI介于27.0~29.9 (e) BMI大于30图4 BMI在不同ε取值下加噪前后的疾病统计分布 在实验对比测试中发现当ε=0.36时统计结果与原始数据统计结果逼近且数据的安全性也得到了保障,当ε=0.1时统计结果的波动十分明显,尤其是在BMI小于18.5的数据上非常明显。原因可能是因为小于18.5的统计数据量过少而添加的噪声过大。 根据年龄数据在ε=0.33, 0.2, 0.1与0.05时的加噪前后的疾病统计分布如图5所示,分别统计在年龄小于20岁、年龄在20~39岁、40~59岁、60~79岁,以及年龄大于80岁的不同条件下数据加噪前后的疾病统计分析结果分布。 (a) 年龄小于20 (b) 年龄介于20~39 (c) 年龄介于40~59 (d) 年龄介于60~79 (e) 年龄大于等于80图5 年龄在不同ε取值下加噪前后的疾病统计分布 可以看出,当ε=0.33时统计结果与原始数据统计结果相近,当ε=0.05时数据的统计结果波动较大,尤其当年龄小于20岁和大于80岁时,疾病的数据差异非常明显,统计误差较大,原因可能与原始数据统计量较小和添加的噪声过大有关。 按差分隐私的定义,当ε取值越小对原数据所添加的噪声值越大,数据的安全性越高,但可用性会降低。实验中我们研究了不同的隐私保护参数ε的取值对于统计结果的影响程度,通过图3-图5的对比实验发现在按性别分类统计时ε取值为0.005时、在按BMI分类统计时ε取值为0.36时、在按年龄分类统计时ε取值为0.33时加噪后的数据误差较小,故而安全性和可用性相对较好。 本节对以上方案的时间开销进行对比,按性别、BMI、年龄不同属性进行差分隐私保护时的时间开销如图6所示。其中:斜线填充表示性别数据为不同ε取值时的时间开销,最大时间开销是7.858 s,最小时间开销是7.835 s;深灰填充表示BMI数据为不同ε取值时的时间开销,最大时间开销是0.299 s,最小时间开销是0.296 s;白色填充表示年龄数据为不同ε取值时的时间开销,最大时间开销是0.305 s,最小时间开销是0.290 s。因为对隐私保护参数的取值和采用的加噪机制不同,时间开销也有所不同,但从实验数据可以看出,不同隐私保护参数取值时的时间开销差异比较小。 图6 性别、BMI、年龄不同属性在不同ε取值时的时间开销 本文提出一种基于差分隐私的可根据不同隐私保护需求进行不同参数设定的健康医疗数据隐私保护方法,该种方法的优点在于相较于传统的隐私保护方法,在当攻击者拥有强大背景知识的情况下差分隐私依旧能够有效地保护隐私信息,同时它严谨的统计学模型对隐私保护强度进行量化,从而可以较好地在隐私保护强度与可用性之间进行权衡。我们通过针对不同类型的数据使用不同的差分隐私机制对其进行加噪处理,同时根据数据类型的不同选取控制隐私保护参数ε的取值使得数据在可用性和安全性上取得一个相对的平衡,控制误差参数δ和满足误差的统计个数θ的取值以保证数据的可用性和安全性更进一步依据处理需求的得到平衡。在数据采取不同的机制进行差分隐私处理之后,数据拥有者可把处理后的数据发布给数据使用者用于数据挖掘相关的分析研究。通过实验分析发现,在误差参数δ和数值型与非数值型数据满足误差的统计个数θ的取值分别为20%、20和10的要求下,对于年龄字段的ε取值为0.33,对于BMI字段ε的取值为0.36,对于性别字段ε的取值为0.005时,在数据的可用性和安全性上有个相对好的平衡。该方法改变对原始数据的扰动程度进而平衡数据的可用性和安全性,使得发布后的医疗数据在仍旧保留整体信息可研究性的前提下保护数据拥有者的隐私。未来的研究工作将探究健康医疗数据共享时动态数据的隐私保护方法。4 实验结果与性能分析
4.1 实验结果
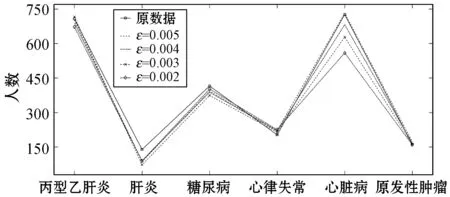

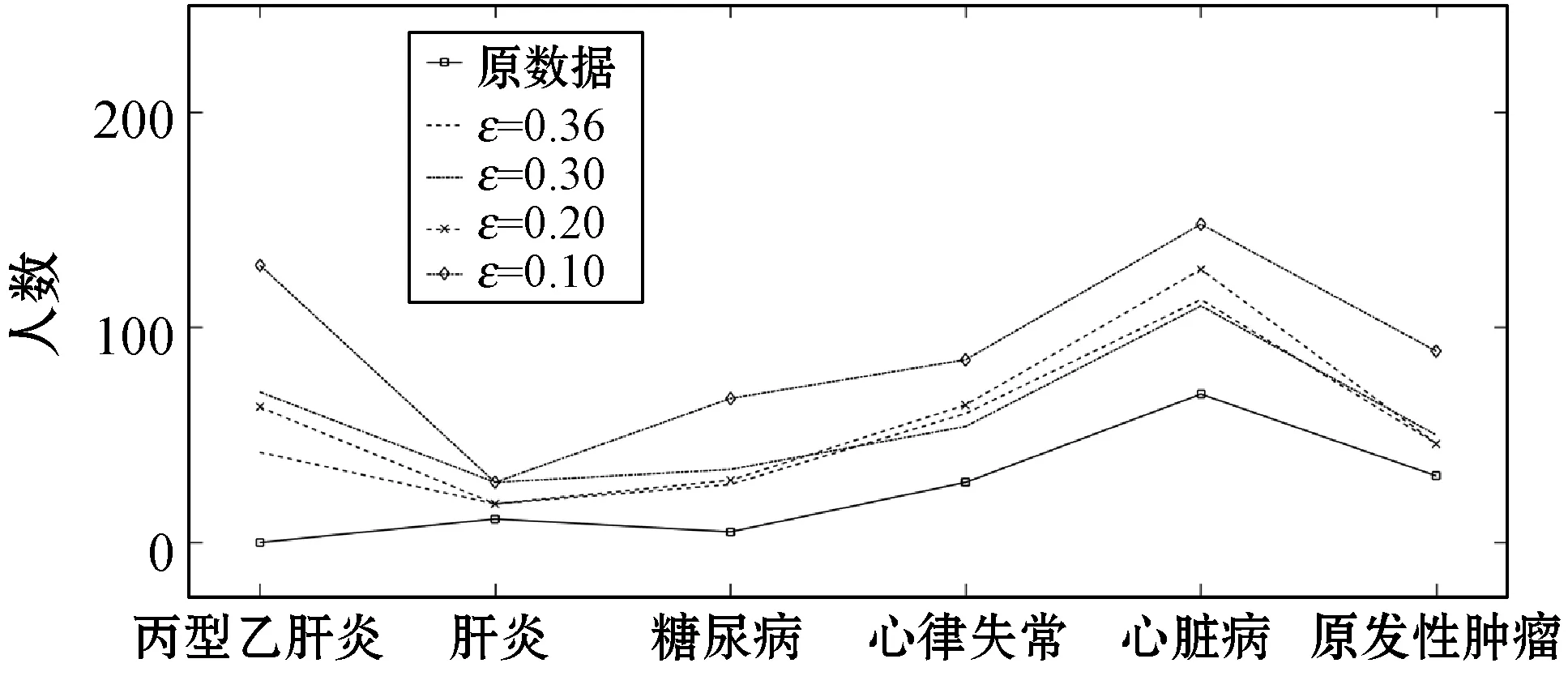



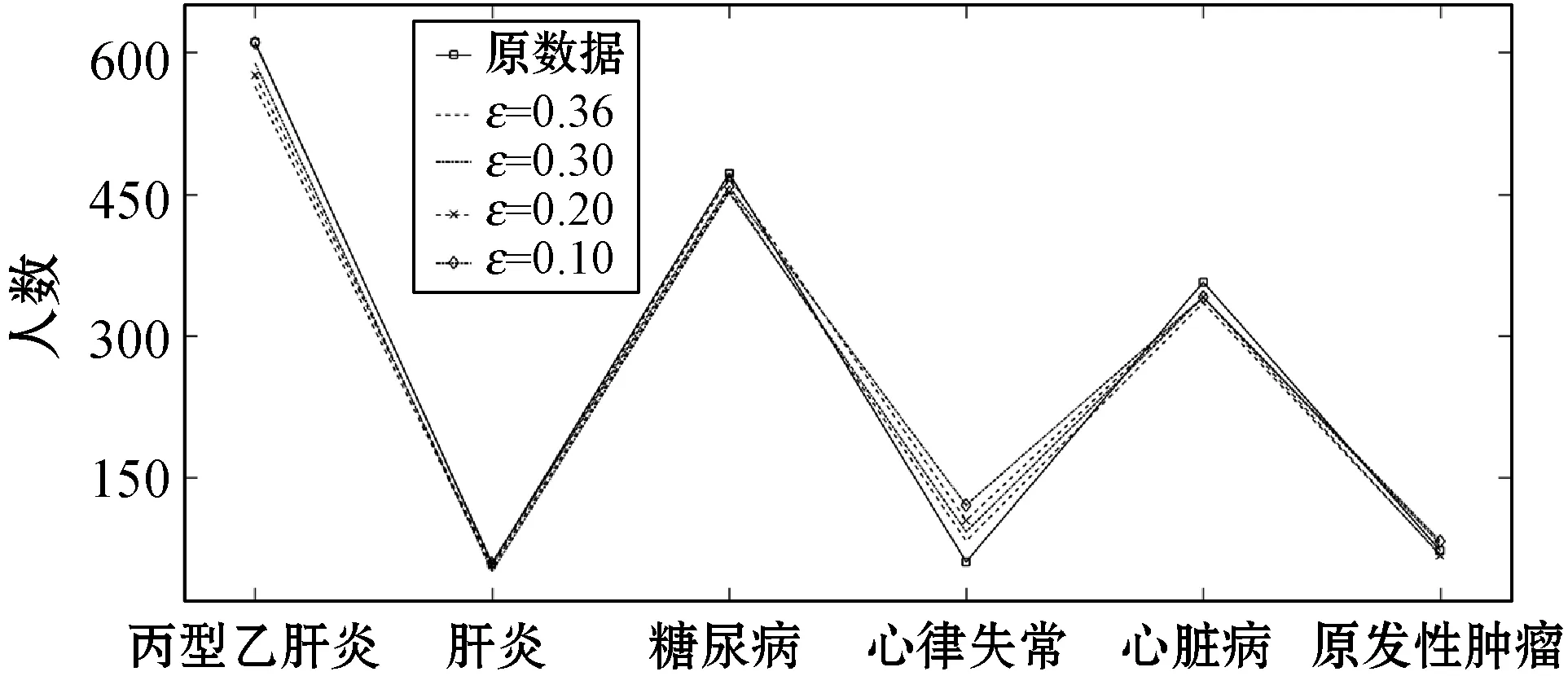

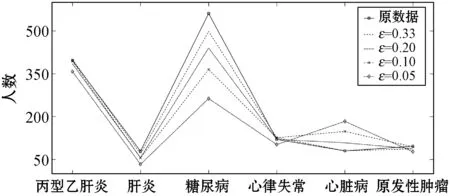


4.2 性能分析

5 结 语
