考虑时变激励的滚动轴承局部故障动力学建模
2022-09-07李昊泽贺雅冯坤江志农冯飞飞
李昊泽,贺雅,*,冯坤,江志农,冯飞飞
1. 北京化工大学 发动机健康监控及网络化教育部重点实验室,北京 100029 2. 北京化工大学 高端机械装备健康监控与自愈化北京市重点实验室,北京 100029 3. 国营川西机器厂,成都 611900
滚动轴承是航空发动机的关键部件之一,其工作可靠性直接关乎发动机的安全、稳定运行。以中国军用航空发动机转子的支承轴承为例,由于其长期工作于高温、高转速、多变工况等恶劣环境中,导致发动机轴承极易发生故障。振动分析是实现发动机轴承故障分析的主要手段,然而中国军用航空发动机主轴承的故障检测仍主要在地面低速运行阶段开展,未实现在服役过程中轴承状态的实时监测与状态评估。目前中国航空发动机在服役过程中出现轴承故障后往往难以在第一时间被发现和预警,直至故障严重劣化。而发动机主轴承故障进一步劣化可能导致转子出现抱死、断轴,甚至会造成机毁人亡的灾难性事故,严重影响了发动机的安全性和作战水平。中国航空发动机轴承故障监测的技术现状主要受限于以下两方面因素:① 对滚动轴承故障机理研究仍不足。动力学建模是滚动轴承故障机理分析的重要手段,但现有建模研究中对激励力简化较多、对接触过程的时变特性考虑较少,导致模型设置与实际故障发生、变化过程存在明显差异,而航空发动机轴承存在显著的时变工况特性,进而模型所得故障机理难以完整描述实际物理过程。② 航空发动机振动信号在外机匣上进行检测,轴承至振动传感器之间信号传递路径复杂导致了故障特征在传递过程中大大衰减、被噪声湮没,因此从采集到的振动信号中提取滚动轴承故障特征需要研究对应、复杂的特征提取算法。然而,研究有效故障特征提取方法的前提是准确掌握故障机理。
因此,拟开展滚动轴承故障的动力学建模研究,优化模型中激励的设置,并考虑其时变特性,使其进一步接近航空发动机轴承的故障特性,进而研究符合航空发动机轴承的故障机理,以指导发动机轴承的故障诊断与状态评估。
许多学者通过建立轴承的局部故障动力学模型,对轴承振动的机理展开研究。McFadden和Smith综合轴承的尺寸、受力以及信号的产生和传递等因素,将局部故障简化为脉冲激励,建立轴承的振动模型,研究单一故障对轴承振动特征的影响。张中民和张耀强等用建立函数模型的方法,综合考虑轴承的尺寸、转速、载荷分布及振动传递函数等因素,用脉冲力序列模拟故障,通过不同的参数取值模拟工况变化,建立模型研究滚动轴承内外圈及滚动体故障的振动特征。曹冲锋等将轴承系统简化为弹簧-阻尼系统,用矩形脉冲模拟轴承故障,通过改变脉冲序列的分布,模拟故障位置、载荷分布等因素对轴承振动特征的影响,基于运动学和动力学理论建立轴承外圈局部故障的振动模型。陈果通过设定矩形分段函数的方法模拟内外圈和滚动体的故障激励,建立了包含机匣、转子和轴承的耦合动力学模型,并用小波包络谱分析提取故障特征,验证了模型的有效性。上述模型中大多是将轴承故障激励简化为脉冲序列,没有考虑具体故障形态的影响,而在实际应用中,滚动轴承故障形态各异,滚动体经过故障的过程及进一步的故障激励模式都会有所不同,从而影响轴承故障的振动特征分析。
为提高建模准确性,Patil、Liu、刘静等提出用半正弦函数模拟滚动轴承的局部故障,建立非线性动力学模型仿真了不同尺寸、不同位置的局部故障,但是半正弦函数并不能完整表示滚动体与局部故障的接触过程。关贞珍等在正常轴承模型的基础上,考虑速度、载荷对周期性脉冲力的影响,以及瞬时间隙改变引起的接触力变化,设定故障激励函数,建立故障轴承的多自由度动力学模型。Behzad等将滚动轴承局部故障产生的冲击激励用随机动态力表示,研究了局部故障对轴承振动响应特征的影响规律,然而这种随机位移激励不能准确描述滚动体与故障的接触情况。刘静通过建立不同激励模式的轴承局部故障的模型,分析滚动轴承局部故障边缘形貌特征演变的内部激励机制,研究滚动轴承故障激励机理。上述研究虽然考虑了滚动体经过故障的时变特性,但未具体分析故障形态、尺寸等因素,仍将轴承局部故障的位移激励设定为矩形激励函数或是简化的半正弦激励函数,尚未进一步分析故障形态、尺寸对时变位移激励的影响。
除了时变位移激励,滚动体与局部故障的接触过程还存在瞬时的撞击力激励。Khanam等建立了冲击脉冲序列与局部故障尺寸、轴承载荷及运行速度的函数,研究滚动体与故障边缘接触的冲击激励机制,并用实验的结果进行验证。黄文涛等在Hertz接触理论的基础上引入与转速相关的撞击力作用,与轴承的尺寸参数以及故障特征结合,建立了内圈单一故障的仿真模型,但是该模型没有阐明撞击力与故障尺寸的变化关系。罗茂林等根据撞击前后的能量守恒关系得到撞击力的作用函数,建立了考虑撞击力的动力学模型,但是该模型没有考虑轴承转速对撞击力的影响。
综上所述,对滚动轴承故障建模和振动特征的研究已经有了长久的发展,但大多数研究是将滚动轴承局部故障简化为单一的位移激励或冲击脉冲激励,与滚动体与故障实际接触过程仍存在一些差距。针对上述问题,建立了一种与滚动体的瞬时位置相关的位移激励函数,并在此基础上提出了与故障尺寸和轴承转速相关的撞击力激励函数,两种激励函数中分别考虑了轴承故障尺寸、轴承运行转速等影响因素,涉及到滚动体经过故障区域时导致的局部接触间隙变化和瞬时撞击力作用,较为全面地反映了滚动体与故障的接触状态。进一步地,基于Hertz接触理论建立了滚动体与局部故障接触的故障激励模型。利用所建立的模型研究了故障尺寸对轴承振动特征的影响规律,用于指导滚动轴承的状态评估和定量诊断方法的建立。
1 局部故障的时变激励模型
当滚动体进入滚道局部故障区域,会与局部故障边缘接触,滚动体的运动轨迹出现偏离,局部接触间隙发生突变,将这种接触间隙的突变定义为位移激励。此外,滚动体接触故障边缘时存在瞬时的撞击力作用,撞击力的大小与故障尺寸和轴承转速相关。基于上述分析,以轴承外圈局部故障为研究对象,建立了一种虑及故障尺寸和轴承转速的完备时变激励模型。
1.1 时变位移激励函数
圆柱滚子经过存在局部故障的滚道表面时有两种接触状态:当局部故障尺寸小于滚动体接触长度时,滚动体不会陷入故障区域,仅存在局部接触刚度的变化;当局部故障尺寸大于滚动体接触长度时,滚动体进入故障区域会发生径向位移的突变。主要研究径向位移突变产生的故障激励。
如图1所示,滚道表面存在宽度为的局部故障,深度为,为瞬时的径向位移激励,为轴承的几何中心,、分别为滚动体中心在不同时刻的位置。瞬时位移激励大小与滚动体进入故障区域的距离以及局部故障的尺寸有关。
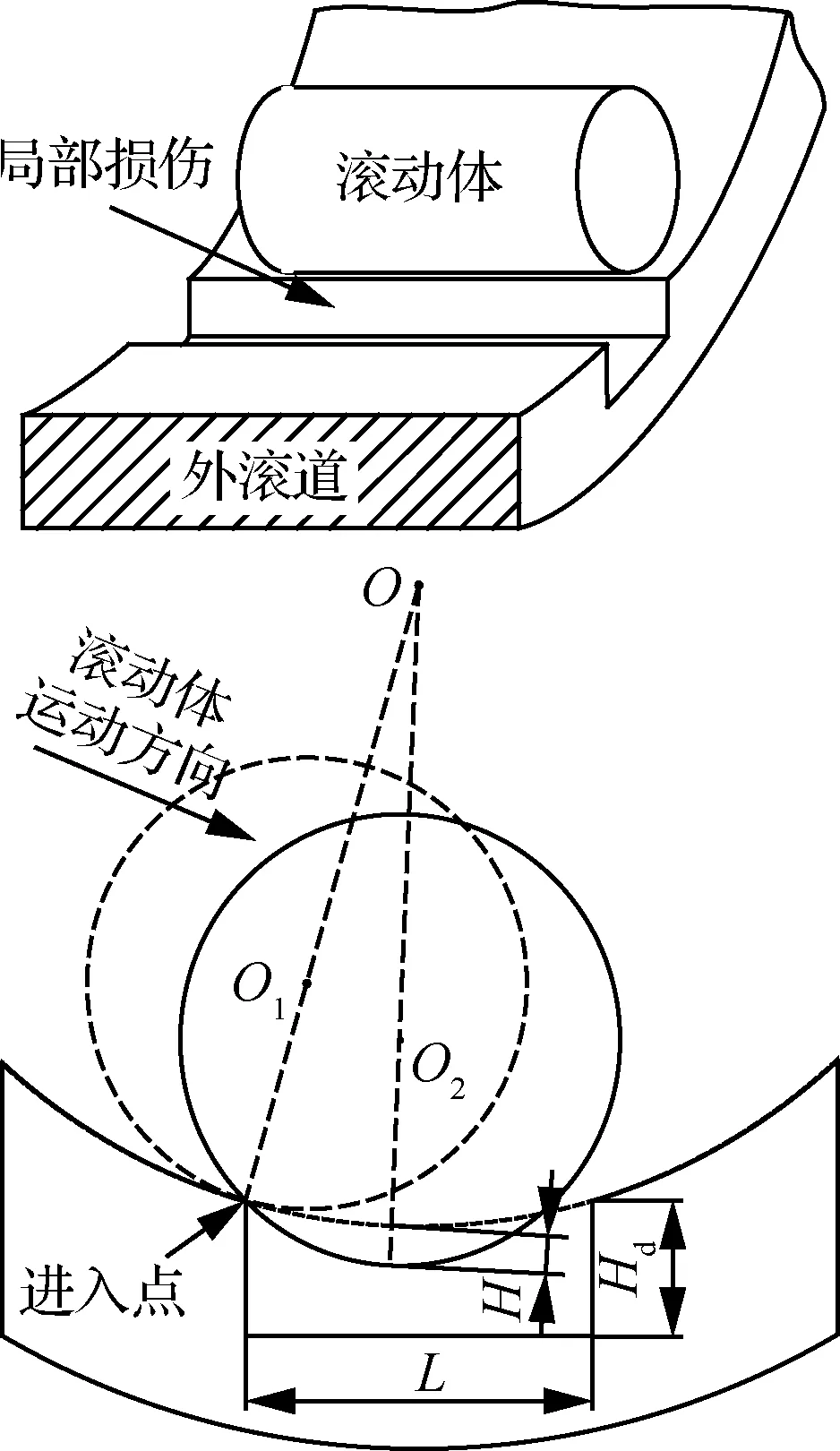
图1 滚动体与局部故障之间的接触关系Fig.1 Contact relationship between roller and local fault
针对上述情况,Liu等提出了一种基于半正弦函数描述的简化故障函数模型,用函数描述了故障引起的时变位移激励。然而,瞬时的位移激励与滚动体的相对位置、故障尺寸等因素有关,单一的半正弦函数不能准确描述局部位移激励在轴承转动过程中的变化情况,因此通过计算滚动体在故障区域瞬时相对位置对应的间隙,实现时变位移激励的准确描述,从而较为准确地还原这个过程。
滚动体在故障区域的尺寸关系如图2所示,为滚动体半径,为内滚道半径,滚动体中心与故障中心的夹角为,故障区域的范围角为,则滚动体进入故障区域的角度可以表示为
=-
(1)

滚动体进入故障的距离为
=sin
(2)
故障引起的瞬时位移函数表示为

(3)
因此,滚动体经过故障区域的位移激励函数表示为
=

(4)
式中:为第个滚动体在时刻的角位置,表示为
=2π(-1)++
(5)
式中:=1,2,3,…,,为滚动体数目;为保持架角速度;为时间;定义为第1个滚动体在零时刻相对轴正方向的角位置。

图2 滚动体进入局部故障的尺寸关系Fig.2 Dimension relation of roller entering into local fault
1.2 引入速度的瞬时撞击力
除了接触间隙的突变,滚动体经过故障区域时还存在瞬时的撞击力作用。如图3所示,当滚动体到达故障中心位置时,与故障边缘接触发生撞击,产生额外的撞击力作用。与现有撞击力函数不同的是,本文的撞击力函数在时变位移激励函数的基础上,综合考虑了故障尺寸以及轴承转动速度对撞击力的影响,改进了原有滚动体径向速度计算方法,从而提出一种瞬时撞击力激励函数。参考文献[19]和[20],在滚动体撞击滚道故障边缘的瞬间,根据冲量定理可推导出瞬时撞击力的大小与滚动体的质量直接相关,同时考虑到滚动体与保持架之间不是刚性连接,因此本文在分析瞬时撞击力作用时以单个滚动体为研究对象。
滚动体进入故障区域后存在切向的速度和径向的速度,而径向的附加位移变化可以用1.1节提出的时变位移激励表示,用的一阶导数表示为

(6)
整理得到滚动体在故障区域内沿径向的瞬时速度表达式为
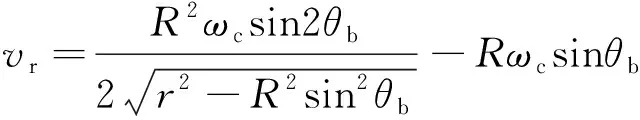
(7)
假设外圈固定不动,滚动体从前边缘撞至后边缘撞击点,对滚动体在径向用冲量定理可得
Δcos=
(8)
式中:为撞击力;Δ为撞击力作用时间;为滚动体质量;为撞击力方向与径向的夹角;根据几何关系可得
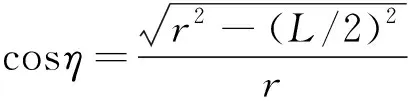
(9)
撞击力作用时间Δ定义为滚动体从撞击故障后边缘至离开故障区域的时间,计算表达式为

图3 滚动体撞击故障边缘示意图Fig.3 Diagram of roller impacting on fault edge

(10)
瞬时撞击力的计算表达式为


(11)
根据撞击瞬间的接触状态,滚动体与故障边缘接触时的几何关系为
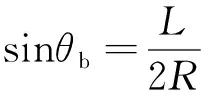
(12)

(13)
撞击力计算公式可以简化为
=
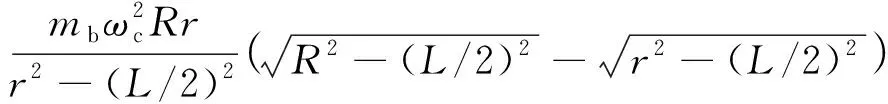
(14)
图4为式(14)反映的瞬时撞击力随故障尺寸和转速的变化情况。由图4可以看出,本文提出的瞬时撞击力模型与故障尺寸、轴承转速呈正相关。随故障尺寸和轴承转速的增大,瞬时撞击力也随之增大,可认为本文建立的瞬时撞击力模型能够较准确地模拟滚动体经过滚道故障区域时的实际撞击情况。

图4 瞬时撞击力随故障尺寸和轴承转速的变化Fig.4 Change of instantaneous impact force with fault size and bearing rotation speed
2 圆柱滚子轴承动力学模型
为尽可能接近实际滚动轴承的局部接触状况,同时兼顾动力学建模、求解的复杂程度,本文建立圆柱滚子轴承动力学模型时做如下基本假设:① 忽略加工误差的影响;② 滚动体相对于轴均匀分布,滚动过程不存在打滑;③ 滚动体与内外圈滚道之间只产生局部的接触变形,对整体的形状和尺寸没有影响;④ 轴承转动时温度不变,不考虑润滑等因素产生的影响。
基于上述简化条件,将轴承模型简化为弹簧-质量系统,滚动体与滚道的接触形式等效为线性弹簧,同时外圈固定不动,内圈与轴看作整体,分别建立水平和竖直两个方向的运动方程。研究对象为滚动体与故障的局部接触关系,因此,设定的简化条件不会对本文的分析产生影响。
根据设定的简化条件以及刚性套圈假设理论,载荷作用下的轴承内外圈都不发生变形,只产生相应的刚性位移,轴承的变形只和滚动体与滚道局部接触区域的变形有关,对内外圈的整体形状不产生影响。简化的滚动轴承两自由度系统动力学方程为

(15)
式中:为内圈与轴的总质量;为系统阻尼;为滚动体与内外圈滚道的接触刚度;、分别为水平和竖直方向的载荷分量;为第个滚动体与滚道的接触变形。由几何关系可以得到
=sin+cos--
(16)
式中:为径向游隙;为第个滚动体在时刻的角位置,表达式为
=2π(-1)++
(17)
此外,为判断滚动体与滚道接触情况的参数。

(18)
如图5所示,为轴承承载区分布范围角,其表达式为

图5 轴承简化模型及载荷分布示意图Fig.5 Simplified bearing model and load distribution diagram

(19)

圆柱滚子与滚道之间的接触形式为线接触,Palmgren给出了计算圆柱滚子与滚道弹性趋近量的经验公式:
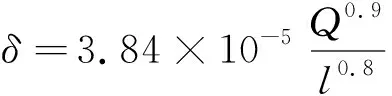
(20)
式中:为滚动体的载荷;为滚动体的长度。
考虑到滚动体直径、滚道直径以及曲率凹凸性的影响,需要对Palmgren公式进行修正,修正后滚动体与滚道的接触刚度表示为
=624×

(21)
式中:=;=;;、分别为滚动体直径和内、外滚道直径。
3 计算结果分析
以某型航空发动机中常用的圆柱滚子轴承为例进行研究,为便于验证模型的有效性,在建模时采用的轴承型号与文中所用实验装置中实际安装轴承型号相同,轴承的安装尺寸、约束条件方面也均与实验装置相同。因此,以实验装置中所用的N205型轴承为例建立轴承外圈故障模型,对其动力学响应进行求解分析。

由于轴承动力学方程组非线性较强,难以得到解析解,利用四阶龙格库塔方法对所建立的动力学模型进行求解,且预设计算步长为Δ=5×10s。

表1 N205轴承几何参数Table 1 Geometric parameters of N205 bearing
3.1 仿真计算结果分析
将表1中参数代入动力学模型中求解得到外圈局部故障振动响应结果如图6所示。从图6(a)中可以看到,轴承的加速度时域信号中存在明显的周期性冲击。对波形进一步做包络分析,得到图6(b)所示的包络谱。其中131.3 Hz频率及其倍频为主导成分。该频率成分与理论外圈故障特征频率基本一致,初步验证了建立的动力学模型的准确性。
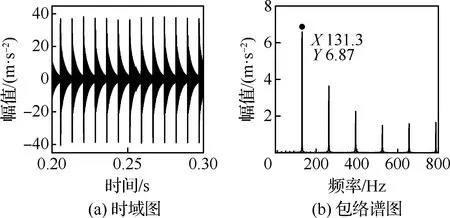
图6 轴承外圈故障仿真振动加速度响应Fig.6 Simulation vibration acceleration response of outer ring fault
为进一步验证提出的轴承动力学模型能有效模拟实际轴承故障振动,利用N205型圆柱滚子轴承开展轴承外圈故障模拟实验。
为深入研究故障机理,同时避免其他因素影响,选择常规滚动轴承实验台进行了故障模拟实验。该实验台虽然结构简单,但在实验过程中充分考虑了如下航空发动机轴承实际情况:
1) 实验件结构与航空发动机轴承接近。本实验选取了圆柱滚子型滚动轴承,该型轴承是航空发动机主体及附件系统常用类型之一。
2) 实验模拟的故障类型与航空发动机轴承一致。疲劳剥落(局部脱落)是航空发动机轴承的常发故障模式,实验通过加工划痕模拟了轴承局部脱落故障。
3) 实验方案根据航空发动机轴承故障诊断方面待解决难题设置。故障识别、不同损伤程度辨识是航空发动机轴承故障诊断方面的待解决难题,实验通过设置不同局部故障尺寸来模拟不同损伤程度的轴承故障。
4) 实验设置与建立的动力学模型相似,便于验证模型准确性。为使实验结果主要集中于故障机理研究,即尽可能避免其他振动成分及信号传递路径的影响,选取了可直接采集轴承座振动信号的常规滚动轴承故障模拟实验台。其故障轴承安装位置距离振动测点的传递路径简单,测试信号受其他因素(如传递路径)影响较小,在一定程度上保持了与建立的简化动力学模型的相似性,能够保证模型验证的准确性。
首先,采用线切割方法在轴承外圈滚道上加工出划痕类局部故障,故障的宽度为0.5mm。然后,将故障轴承安装在如图7所示的旋转设备故障模拟实验台上,设置轴承转速为1 500 r/min。实验采用BK 4519传感器(灵敏度为10 mV/g)和LMS SCADA数采设备采集轴承座的振动加速度信号,加速度测点为故障轴承所在轴承座的垂直方向。

图7 旋转设备故障模拟实验台Fig.7 Rotating equipment fault simulation test bench
实测信号振动加速度响应和包络谱如图8所示。可以看出,与仿真信号相比,实际采集的故障波形中不仅存在明显冲击成分,还出现了周期性波动,这主要是实验台中转子自身存在的不平衡质量导致轴承故障产生的周期性成分被转子转频调制的原因。而且,图8(b)的包络谱中含有132.5 Hz成分及其倍频,考虑到实际滚动轴承的滚动体在运行中存在微小滑动等因素的影响,可认为132.5 Hz与理论外圈故障特征频率131.25 Hz基本一致。另外,由于转子转频的调制,包络谱中132.5 Hz及倍频周围出现了明显的转频间隔,这是转频调制周期冲击成分的现象在频域上的体现。综上,本文建立的轴承局部故障动力学模型能有效模拟实际轴承故障,可用于分析研究轴承故障振动特征。

图8 轴承外圈故障实测振动加速度响应Fig.8 Measured vibration acceleration response of outer ring fault
3.2 与传统轴承动力学模型的对比分析
为体现出本文建立模型的优越性,本小节建立了两种传统轴承动力学模型:① HEM(Half-sine Excitation Model)表示仅考虑半正弦激励函数的模型;② HECFM(Half-sine Excitation and Constant Impact Force Model)表示同时考虑半正弦激励和恒定撞击力作用的模型。采用TDFEM(Time-varying Displacement and Impact Force Excitation Model)表示本文提出的时变位移和撞击力激励模型。利用两种传统的轴承模型,设置外圈故障尺寸为0.5 mm,通过设定不同的轴承运行转速,求解出外圈局部故障振动响应,并与模型求解结果进行对比分析,探究所用的位移激励函数和考虑瞬时速度的撞击力对振动响应的影响规律。
图9为3种轴承模型仿真结果的振动加速度有效值随着轴承转速的变化趋势。可以看到,轴承转速从1 500 r/min增加到2 100 r/min过程中,建立模型的仿真加速度响应有效值整体上呈增长趋势,即瞬态速度冲击对振动响应的影响是正相关的。相比两种传统模型,建立的轴承模型结果随着转速的变化速度明显更高,这是由于其除了考虑撞击力的因素,在撞击力的计算中同时依据实际情况引入了瞬时转速的影响,所以反映振动能量水平的有效值也增大。另外,从两种传统模型结果可以看出,与转速无关的恒定撞击力作用对振动响应的影响不大,同时体现出了引入瞬时转速的必要性。对比分析结果表明,相比传统的轴承动力学模型,本文建立的故障模型能更有效地模拟实际滚动轴承的振动特性。

图9 不同轴承转速下振动加速度有效值Fig.9 RMS of vibration acceleration response for different bearing speeds
3.3 故障尺寸对振动特征影响的仿真及实验
滚动轴承在实际运行过程中大多是会经历一个从故障萌芽发展到可见缺陷的过程,因此研究轴承在不同故障阶段的振动特征有利于对于实际滚动轴承故障状态进行准确评估。因此,利用不同的外圈故障尺寸来模拟滚动轴承外圈处于不同故障阶段的状态,并对仿真和实验的加速度振动响应进行了对比分析。
首先,利用本文建立的动力学模型计算出不同故障尺寸下的振动加速度响应。设置轴承工况条件与3.1节中一致,分别设置外圈故障尺寸为0.5、1、2、4 mm,求解出不同故障尺寸下轴承的振动加速度响应,如图10所示。随着外圈故障尺寸的增大,时域波形中周期性冲击频率未发生变化,冲击能量明显增大,同样从包络谱中可以看出,故障特征频率及其倍频值保持一致,但其幅值会随着故障尺寸的增大发生明显变化,在故障尺寸增大到2 mm以上,特征频率幅值增大速度明显变缓,可见,特征频率幅值会在故障发展到某一阶段时出现突增,整体上不会随着故障尺寸的增大而增大,因此采用该特征指标难以准确评估轴承故障状态,还需要结合其他统计特征值进行综合评估。

图10 不同故障尺寸下轴承外圈故障仿真 振动加速度响应Fig.10 Simulation vibration acceleration response of bearing outer ring fault of different sizes
然后,在实验台上进行轴承外圈在不同故障尺寸下的故障模拟实验,分别在N205型轴承外圈滚道上加工宽度为0.5、1、2、4 mm的划痕模拟不同故障阶段,如图11所示。数据采集设备、运行工况及振动测点与3.1节中一致,分别采集不同故障阶段的轴承振动加速度信号,并进行包络谱分析,如图12所示。

图11 不同故障尺寸的轴承外圈实验件Fig.11 Bearing outer ring test pieces for faults of different sizes
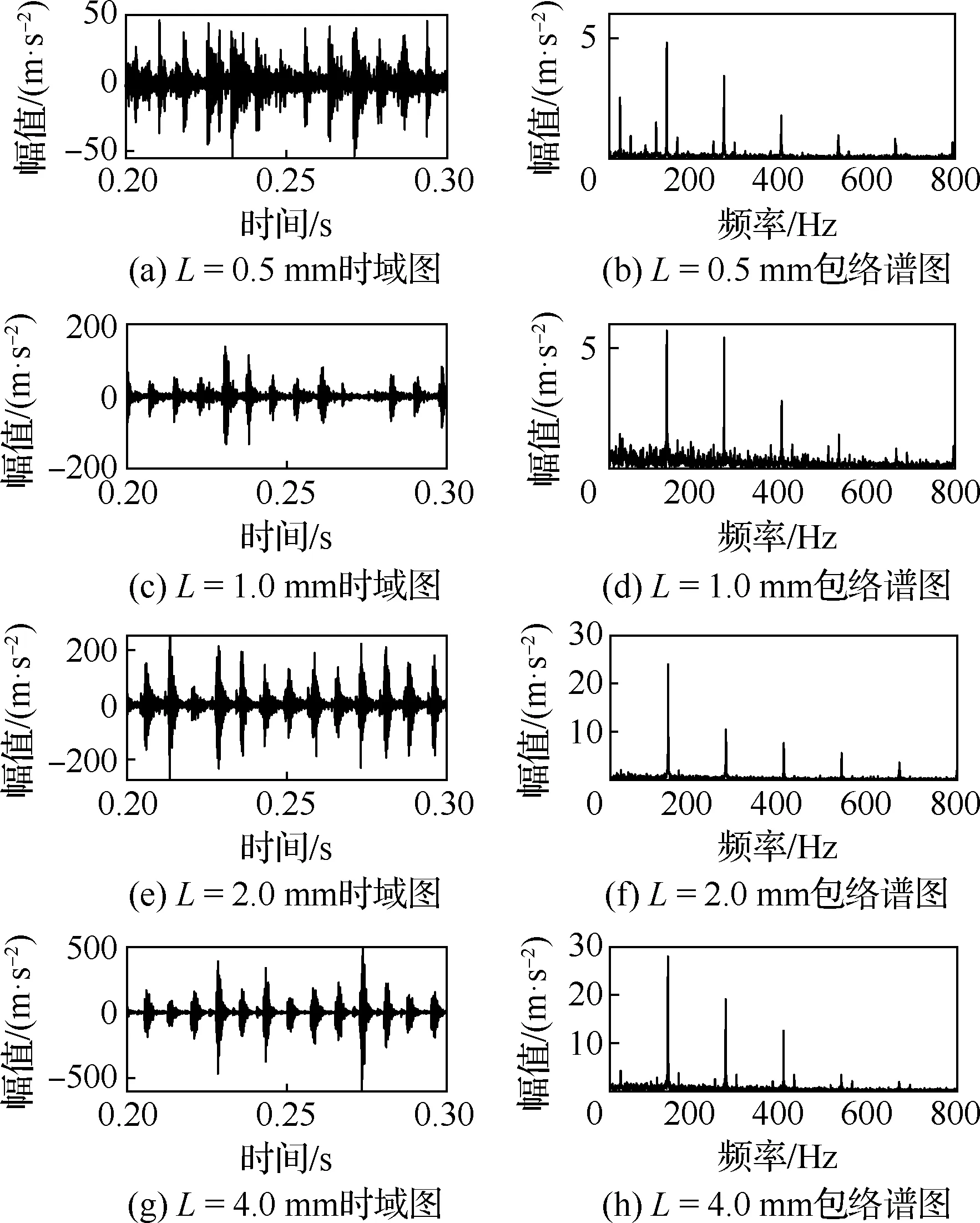
图12 不同故障尺寸下轴承外圈故障实测振动 加速度响应Fig.12 Measured vibration acceleration response of bearing outer ring fault of different sizes
从时域波形可以看出,随着外圈故障尺寸的增大,轴承振动水平有明显提高,虽然由于其他振动、噪声等因素的干扰,周期性冲击现象在时域上不再显著,但在包络谱中仍然能够能看到明显的故障特征频率。与仿真信号类似,随着故障尺寸的增大,故障特征频率幅值会在某一故障阶段发生突增,在早期或晚期阶段都未呈现出明显的增长趋势,这也验证了本文所建立的轴承故障振动模型的准确性。另外,从图12(b)、12(d)、12(f)和12(h)可以看到,故障尺寸的增大在一定程度上削弱了转频对故障特征频率的调制效应。
为了定量地对比分析仿真和实验信号的振动特征,分别计算仿真和实验信号在不同故障尺寸下的包络谱特征频率幅值和振动有效值,如图13和图14所示。从图中可以看出,仿真结果和实验结果中的两种特征幅值存在一定差距,分析这种差异主要来源于仿真模型中刚度等参数设置的差异、部件之间的耦合作用等因素。虽然当前仿真模型和实验台仍存在一定的差距,不能完全模拟实验工况,但能够看出仿真得到的特征频率与实验结果相同,并且两者的特征参数变化趋势也基本保持一致,一定程度上验证了本文提出轴承动力学模型的有效性,可用于实际应用中分析局部故障尺寸对轴承振动响应的影响。
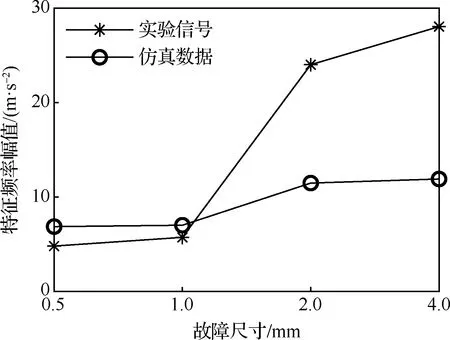
图13 不同故障尺寸下的包络谱特征频率幅值Fig.13 Characteristic frequency amplitude of envelope spectrum for faults of different sizes
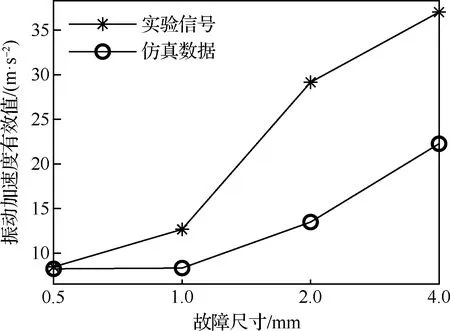
图14 不同故障尺寸下的振动加速度有效值Fig.14 RMS of vibration acceleration response for faults of different sizes
另外,随着轴承故障尺寸的增大,振动有效值整体上呈连续增大趋势,这是因为外圈滚道故障尺寸的增大使滚动体经过故障区域时产生的冲击能量增强,轴承的振动水平增大。相比振动有效值,特征频率幅值整体上的变化趋势略有不同,主要是因为冲击能量在频域上不只体现在特征频率幅值,也体现在多阶倍频成分上。因此在基于特征频率幅值开展滚动轴承状态评估时,还需要考虑包络谱中特征频率多阶倍频成分所包含的振动能量。
另外,随着轴承故障尺寸的增大,振动有效值整体上呈连续增大趋势,这是因为外圈滚道故障尺寸的增大使滚动体经过故障区域时产生的冲击能量增强,轴承的振动水平增大。相比振动有效值,特征频率幅值整体上的变化趋势略有不同,主要是因为冲击能量在频域上不只体现在特征频率幅值,也体现在多阶倍频成分上。因此在基于特征频率幅值开展滚动轴承状态评估时,还需要考虑包络谱中特征频率多阶倍频成分所包含的振动能量。
近年来,基于数据学习的滚动轴承故障智能诊断方法发展迅速,不同工况下训练样本与测试样本的数据分布差异性促进了迁移学习在故障诊断领域的应用。但对于不同故障尺寸的轴承振动数据分布特征研究较少,因此,通过计算同一工况下不同故障尺寸的30组振动加速度有效值及特征频率幅值,构成二维特征空间,分析不同故障阶段下轴承振动特征的多维分布特点。其中,为模拟出特征的分散性,在仿真的轴承加速度信号中加入了信噪比为0.8 dB的高斯白噪声。图15为仿真和实验信号的振动特征参数在二维空间中的分布情况。

从图15可以看出,随着故障尺寸的变化,轴承故障振动响应特征和正常数据特征在二维空间中分布的距离会发生明显的变化。利用本文建立的轴承动力学模型,通过模拟不同故障阶段的轴承振动信号,研究数据分布随故障发展的变化特征,可为基于数据驱动的轴承故障智能诊断方法提供理论指导。
4 结 论
1) 以圆柱滚子轴承外圈故障为研究对象,基于Hertz接触理论建立了一种新的考虑时变位移激励和瞬时撞击力的滚动轴承振动动力学模型。与以往不同的是,本文的时变位移激励函数是建立在滚动体在故障区域瞬时相对位置对应间隙的基础上,并且本文在撞击力作用函数中引入故障尺寸和轴承转速等影响因素,以更为准确地表征滚动体与故障区域的接触过程。
2) 通过N205滚动轴承外圈故障振动实测信号与本文所建立的振动模型求解得到的仿真信号进行对比分析。结果表明本文建立的轴承故障振动模型能准确模拟实际滚动轴承故障特征频率,可有效预测故障特征频率幅值、有效值等一维振动特征及其构成的多维特征分布随故障尺寸的变化情况。
