太阳能无人机伞降着陆多体动力学仿真与试验

王睿，周洲，郭荣化，黄悦琛

1. 西北工业大学 航空学院，西安 710072 2. 中国人民解放军63870部队，渭南 714200

近年来小型无人机以较高的费效比和灵活的使用方式得到了广泛地应用。为了减小对场地的依赖，采用降落伞进行伞降回收是小型无人机常见的着陆方式。但是伞-机系统受环境尤其是风的影响很大，而伞-机系统的运动关系复杂，伞的展开过程容易相互干涉发生危险。尤其是针对太阳能无人机等低翼载荷的无人机，由于飞行速度低，伞的展开过程对无人机的姿态扰动更大；在稳定下降段，因为无人机的下降速度与巡航速度相当，所以在这个过程无人机的气动力不可忽略。这些因素使得太阳能无人机的伞降过程更复杂，需要对这一过程进行更深入地分析研究。

一个典型的无人机伞降回收工作过程主要包含以下阶段：① 进入伞降回收状态；② 打开伞舱，弹出引导伞；③ 拉出主伞包，并将伞绳、主伞伞衣拉直；④ 主伞初始充气；⑤ 主伞收口解除，进入主充气直到充满；⑥ 机/伞动力学平衡，稳定下降；⑦ 接地，切伞。其中，影响最大的是拉直、充气、稳定下降阶段。

张青斌等对降落伞拉直过程中的“绳帆”现象进行了研究，结合有关绳索动力学以及多体动力学的研究成果，分别采用多刚体模型和阻尼弹簧模型建立了降落伞拉直过程的动力学模型。针对翼伞系统稳定飞行的运动特性，将其处理为伞衣、伞绳和载荷等多刚体系统。利用多项式形式表示伞衣下拉后缘时的气动力，附加质量影响处理为等效力，发现所建模型有效反映了翼伞系统的相对运动，可通过改变连接方式提高载荷运动的稳定性。王海涛研究了带牵顶伞和剥离带的大型降落伞拉直过程分阶段动力学建模问题，分析和评估了牵顶伞和剥离带对抽打现象的作用。通过仿真分析了降落伞系统的运动稳定性，得出降落伞系统的姿态变化规律。郭鹏根据实验现象，对航天器回收系统的大型降落伞开伞过程进行了详细的分析建模研究，获得了大型降落伞的拉直、充气等过程的详细模型。Accorsi等采用有限元方法研究降落伞的动力学行为。其中，考虑了伞衣的大变形与空气动力的强耦合作用，对动力学方程的质量矩阵和刚度矩阵进行修正，对十字形伞、环形伞等伞降过程从充气到稳定下降过程进行了仿真，获得了伞衣充气过程的精确描述。这些方法对飞行器本体的考虑较少，在航空领域，回收过程飞行器的空气动力学仍起一定作用，飞行器本体的影响不可忽略，因此这些方法不能完全适用。

Opazo和Langelaan分析了从降落伞中空投多旋翼飞行器的稳定飞行和安全过渡到有动力的控制问题。该论文主要聚焦于飞行器本体的稳定性与控制，但是降落伞对飞行器的影响考虑较少。Wise研究了带翼伞的小型无人机的动力学特性，所采用的是八自由度的动力学方程，由于考虑了绳索的动态特性和控制特性，所以该方法的动力学方程的刚性很强，使微分方程的求解非常缓慢。刘志强建立了风速为零时的无人机伞降回收系统，得到了无人机伞降回收速度、开伞高度、开伞时间和回收轨迹及姿态的关系，确定了最佳的回收轨迹及姿态。但是该论文采用的是6自由度的动力学模型，缺乏对伞、机系统的相对运动的描述，而且也未考虑风对无人机回收的影响。丛书全和姜杨充分利用风向和无人机回收时随风水平漂移的特点，在不改变原回收区基础上，改进无人机飞控算法，得到了一种可调节的无人机回收方法。但是该方法未考虑降落伞打开的动态过程，因此动力学特性模拟精度不足。吴翰等基于凯恩方程方法推导了无人机伞降回收系统的多体动力学模型，通过平板绕流系数优化了伞降过程的大迎角空气动力特性，并与飞行试验数据进行了对比。但是，该文没有考虑降落伞与无人机之间的相对运动，仅能描述从降落伞完全拉直到和无人机一起稳定下降的运动过程，因此对初始阶段降落伞对无人机的姿态扰动模拟不充分。席庆彪等针对小型无人机伞降回收特点, 设计了用于该系统的定点回收系统，建立了基于风场扰动的回收模型，确定了相应的控制策略与控制结构，同时建立了相应的回收飞行段导航控制任务规划，对回收航线调整点位置选定、飞行速度控制以及控制指令发送等进行了约束，有效提高了小型无人机定点降落的准确度问题。郑浩奕讨论了无人机伞降系统的关键技术，从定点回收技术的动力学模型、开伞减速和漂移状态3方面进行了详细分析，针对风向和风速对无人机的安全降落回收有很大影响的问题，提出了根据风向和风速调整伞降回收策略的方法。丁娣等针对无人机伞降回收系统，设计了无人机伞降回收系统的十二自由度仿真，拓展了无人机伞降回收系统设计方法。发现了基于动力学仿真的设计方法能够考虑除最大许可着陆速度之外的开伞力峰值等其他设计指标，进一步细化了降落伞设计参数选择。关于伞绳与无人机的连接方式的影响，陈自力等建立了动力翼伞8自由度的多体非线性动力学模型，其中伞绳与载荷采用的是两点连接的方式，这种方式与无人机的连接方式并不相同。宁雷鸣等推导了一种伞绳拉力在无人机上的作用点的表示方法，采用迎角与伞绳标称角度的关系简化了问题，但是该方法仅考虑了纵向的情况，未考虑横航向，而且在有风的情况下，无人机的迎角与伞的迎角将不同，这种简化方法将失效。

小型太阳能无人机由于设计成本和周期的原因，一些模型参数并不精确，所以需要找到一种简便可行又能准确反映其伞降特性的研究方法。小型太阳能无人机的飞行速度不高，开伞动载相对不大，但是开伞时的反作用力会对无人机的姿态产生较大的扰动。所以，本文对开伞充气过程选用了半经验的建模分析方法，而且不考虑伞的自转运动，而为了准确分析伞对无人机姿态的扰动，推导了伞绳挂点和结点对无人机的力矩作用规律，并通过数字仿真与飞行试验对比验证了方法的可行性。

1 伞降系统多体动力学模型

小型无人机由于重量不大、伞的展开过程短，伞绳相对也较短，降落伞的自转对无人机的作用力影响较小，所以为了简化该类型无人机的伞降过程，提出了以下假设：① 伞绳的重量计入主伞衣的重量中；② 假设伞绳为直线，不考虑伞绳弯曲的影响；③ 伞绳只在绷紧后产生拉力，松驰时不产生力，伞绳拉力采用阻尼弹簧模型描述；④ 忽 略降落伞和伞绳的三轴转动动力学，它们的角度直接根据空间几何关系求解；⑤ 降落伞不受力矩的作用，伞底面永远和伞绳垂直，伞充满气之后形状不变；⑥ 伞绳在无人机上的挂点组成的平面与无人机的机体坐标系的平面平行。

为了建立伞降系统的多体动力学模型，首先需要分别建立无人机(U)、降落伞(P)和伞绳(R)的坐标系。无人机的体坐标系为：坐标原点在全机重心；轴指向前、轴指向右、轴垂直于平面指向下。降落伞的体坐标系为：坐标原点取为伞底面圆心、轴在伞底面上指向前、轴在伞底面指向右、轴垂直于伞底面指向下。伞绳的体坐标系为：坐标原点在降落伞的主伞绳环上；指向无人机的吊挂绳环方向、指向右、平面与垂直。

1.1 无人机的动力学方程

伞降多体动力学系统中，无人机除了受到常规飞行时的重力、空气动力和推力之外，还受到伞绳的拉力，因此，只需要把伞绳对无人机的作用力和力矩加入到常规6自由度无人机动力学方程中，即可求得伞降多体动力学系统中的无人机动力学方程：

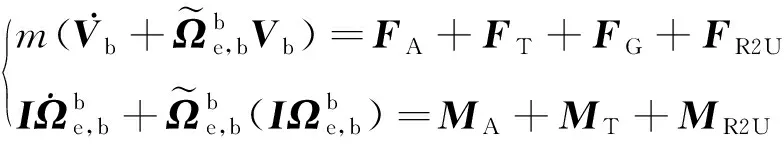
(1)

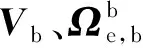
为了方便使用，一般将其在机体坐标系中展开为分量形式，并且补充运动学关系使方程组封闭，成为如下形式：

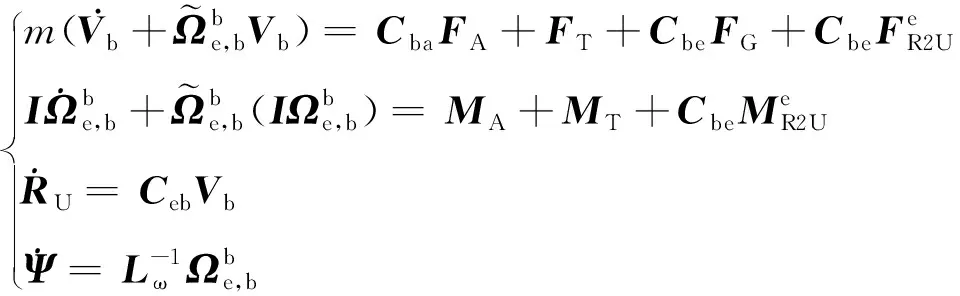
(2)

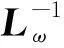
1.2 降落伞的动力学方程

因为降落伞绕自身的转动对无人机的作用力变化量较小，所以为了简化起见，本文忽略了降落伞的三轴自转运动，仅考虑其三自由度平动运动。于是，可以得到降落伞的动力学方程为

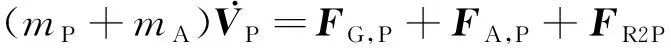
(3)

式中：为降落伞的质量；为降落伞的附加质量；为降落伞相对地面坐标系的线速度。

降落伞的姿态角可以根据几何关系直接解算得到：根据降落伞和伞绳的体坐标系的定义以及伞底面永远和伞绳垂直的假设，伞绳的体坐标系绕转过π/2后与降落伞坐标系重合。据此可以求得伞绳到降落伞的坐标转换矩阵，从而求得地面坐标系到降落伞的体坐标转换矩阵求解公式为

=

(4)

根据该坐标转换矩阵即可求得表示降落伞姿态的欧拉角。

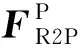
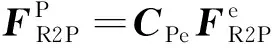
(5)

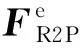
至此，也可以把式(3)在降落伞体轴系中表示为分量形式：

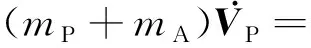
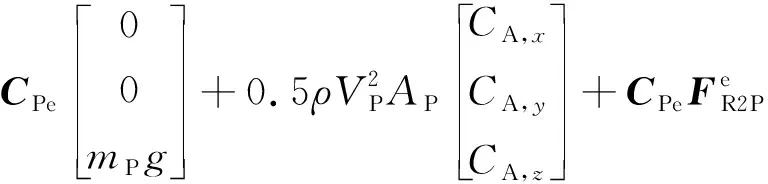
(6)

式中：为降落伞的面积；A,、A,、A,分别为降落伞的三轴阻力系数；为降落伞对地速度的大小；为重力加速度；为大气密度。

2 伞-机系统的受力关系

2.1 降落伞展开过程的受力关系

伞降模型中，最难以确定的是伞的充气、展开过程，以及伞/机系统稳定下降之后伞的受力和运动特性。本文采用半理论半经验方法模拟伞衣的充气和展开过程。

计算伞衣的充气、展开过程时，要求解的2个最主要变量是阻力面积和附加质量。

2.1.1 阻力面积的求解

降落伞的阻力面积定义为

D,=,P

(7)

式中：,P为伞的阻力系数，假设其为常数，根据文献[23]，圆伞的轴向阻力系数取=0.9(对应式(6)中的A,)，侧向阻力系数取为0.3(对应式(6)中的A,和A,)；为伞的面积，该面积与伞的展开程度有关，计算公式为

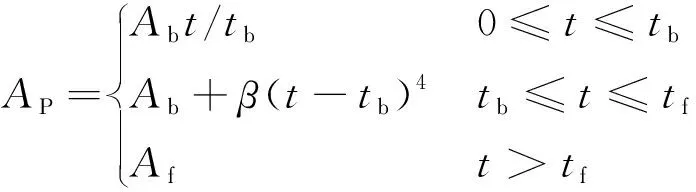
(8)

其中：、、分别为展开所经过的时间、初始充气时间、充满时间；为伞的收口面积;为伞的投影面积；系数的求解公式为

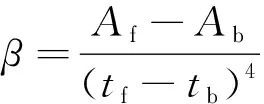
(9)

初始充气时间的求解公式为

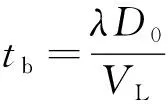
(10)

式中：为伞的名义直径；常数主要取决于伞形，与飞行高度和速度无关，为伞衣拉直速度，由实验测得，透气量适中的密织物平面圆形伞系数=1.74±19%，本文取其平均值1.74；近似为开始拉直时的飞行速度。

充满时间的求解公式为

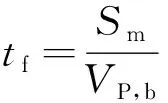
(11)

式中：近似取为主伞开始充气时的飞行速度；为主伞充气过程经过的距离，可由经验公式推得，对于一定伞形来说，与伞的名义直径成比例：

=

(12)

且与初始充气结束时的半径及有效透气量有关。本文取=10。

于是伞的空气动力学阻力为

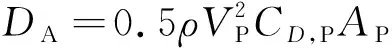
(13)

2.1.2 附加质量的求解

降落伞的非定常空气动力可以采用附加质量方法来表示。附加质量由伞衣内含质量和伞衣表观质量共2部分组成，计算公式为

=+=

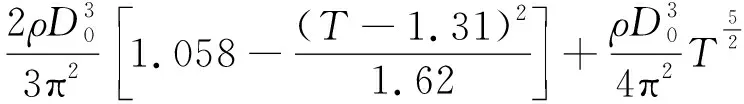
(14)

式中：为无因次充气时间，=。

2.2 伞绳的拉力大小和方向

根据伞绳为直线的假设，若已知伞和无人机在地面坐标系中的坐标，即可计算出伞绳的长度和在地面坐标系中的方向，从而可以求得伞绳的张力和方向。由于忽略了伞绳的质量，因此伞绳对无人机和降落伞的力大小相等、方向相反。降落伞和无人机的多体动力学关系主要通过伞绳进行连接。

伞绳的矢量表达形式为

=-

(15)

式中：为伞绳在地面坐标系的矢量表示，的模即为伞绳的实际长度；为降落伞的坐标原点在地面坐标系的位置矢量。

假设伞绳拉力为阻尼弹簧模型，于是可以求得伞绳的张力大小为

=

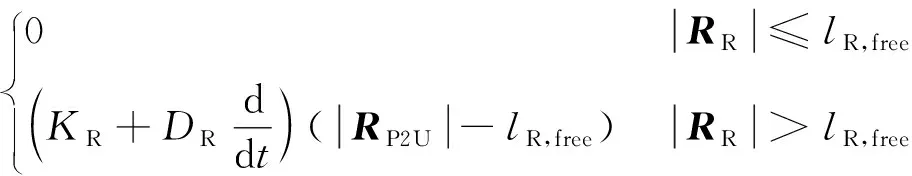
(16)

式中：为伞绳自由状态的长度；和分别为伞绳的弹性系数和阻尼系数；||为伞绳长度。

伞绳相对地面坐标系的角度，采用四元数法根据伞绳的轴与地面的轴的关系求解。

与的夹角满足

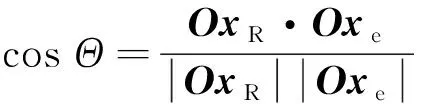
(17)

从到的旋转轴为

=×

(18)

因此，描述伞绳坐标系到地面坐标系的四元数表示为

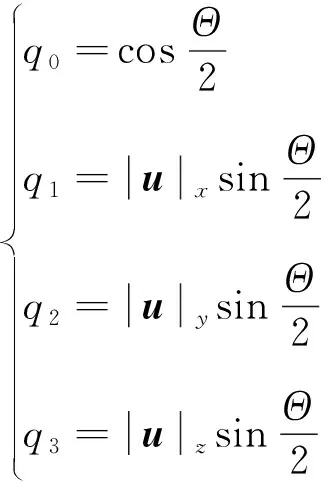
(19)

式中：||、||、||分别表示式(18)中的矢量归一化之后在地面坐标系的、、轴的分量。

根据该四元数，即可求得伞绳坐标系的欧拉角及其与地面坐标系的坐标转换矩阵。于是可以求得伞绳对降落伞的拉力在地面坐标系中的分解形式为

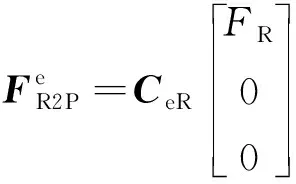
(20)

根据力的反作用原理，伞绳对无人机的拉力在地面坐标系中的分解形式为

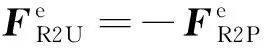
(21)

2.3 伞绳挂点对无人机力矩的影响

假设降落伞在无人机上设置有4个连接点，2个在重心前、2个在重心后，如图1所示，且4个连接点1、2、3、4与机体的平面平行。伞绳对无人机的拉力矢量为，如果拉力矢量与机体的交点在伞绳连接点1234的四边形内，则4根分伞绳都绷紧；如果该交点在1234的四边形外，由于伞绳的柔性特征，将会有某根伞绳不受力，从而使得拉力矢量对无人机的力矩作用点不会超出1234四边形的范围。

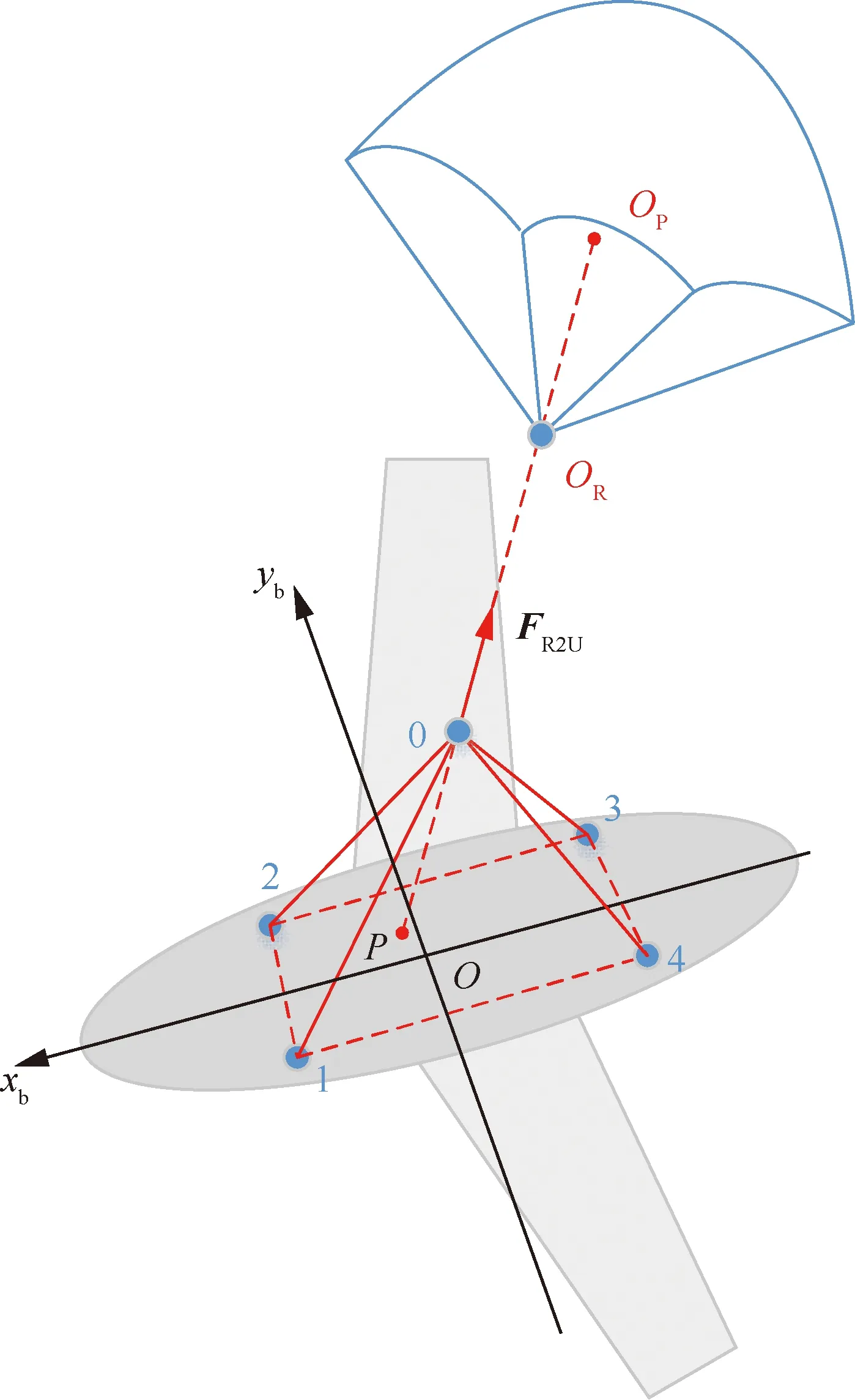
图1 无人机伞降系统的挂点(斜下视图)Fig.1 Hanging point of UAV parachute landing system (oblique view)

因为拉力矢量在主伞绳上，在已知伞和无人机的坐标原点在地面坐标系中的坐标、，以及无人机的吊挂绳环在绷紧状态下在无人机体坐标系中的坐标之后，可以根据空间几何关系求解伞绳的法向量。

无人机的吊挂绳环(图1中的点0)在地面坐标系中的矢量表示为

=+

(22)

式中：为从无人机的机体坐标系原点到无人机的吊挂绳环结点0的矢量。

从伞绳结点0到伞的坐标原点的矢量即为伞绳对无人机的拉力的方向矢量，其计算公式为

=-

(23)

于是即可求得伞绳所在直线上任一点在地面坐标系的参数方程表达式为

=+

(24)

式中：为直线方程的参数。

然后，计算伞绳在无人机上的挂点1、2、3、4构成的平面的表达式。因为假设平面1234与无人机的平面平行，所以无人机的轴即为该平面的法向量，该法向量在地面坐标系中的表达式为

=[0,0,1]

(25)

于是可以求得挂点1234构成的平面上任一点满足以下表达式：

·=0

(26)

因为伞绳所在直线与平面1234的交点同时满足方程式(24)和式(26)，所以联立这2个方程之后，可以求得直线方程的参数为

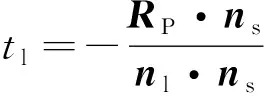
(27)

把该参数代入式(24)即可求得伞绳对无人机的拉力矢量与无人机机体的交点坐标。实际使用中采用它在机体坐标系中的相对位置来进行其它计算更方便，其表达式为

=-

(28)

需要注意的是，式(28)所求得的的自然形式是在地面坐标系中表示的，为了使用方便还需要转化到机体坐标系中。它在无人机机体坐标系的分量形式为

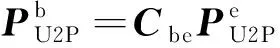
(29)

如上所述，由于伞绳的柔性特点，伞绳对无人机的作用点会被自动限制在挂点1、2、3、4之间的区域内，所以据此对式(29)进行限幅之后所得的点即为伞绳对无人机的拉力的作用点。

在得到了伞绳对无人机的拉力的大小、方向、作用点之后，即可求得伞绳对无人机的力矩如下所示：

=×

(30)

在机体坐标系中展开的分量形式为

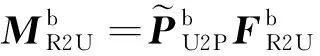
(31)

3 飞行仿真与试验

3.1 算例无人机及其降落伞

算例无人机为“魅影”太阳能无人机，其主要参数如表1所示。

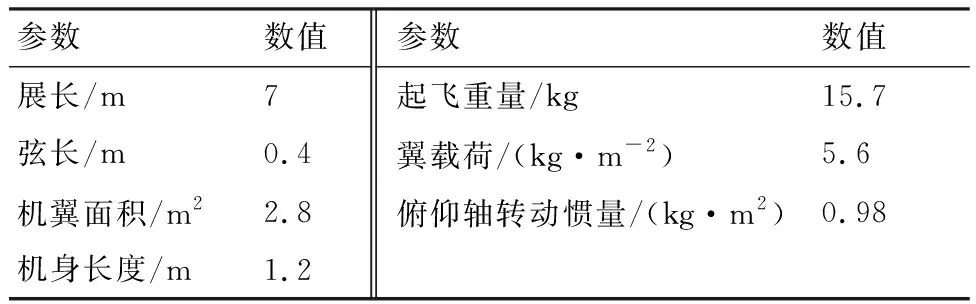
表1 “魅影”太阳能无人机的主要参数Table 1 Main parameters of “Mei Ying” solar-powered UAV

无人机的升力系数、俯仰力矩系数随迎角变化关系曲线如图2所示。所采用的降落伞系统主要数据如表2所示。

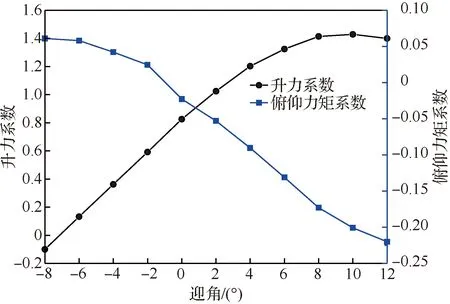
图2 “魅影”无人机的升力和俯仰力矩系数Fig.2 Lift and pitch moment coefficients of “Mei Ying” UAV

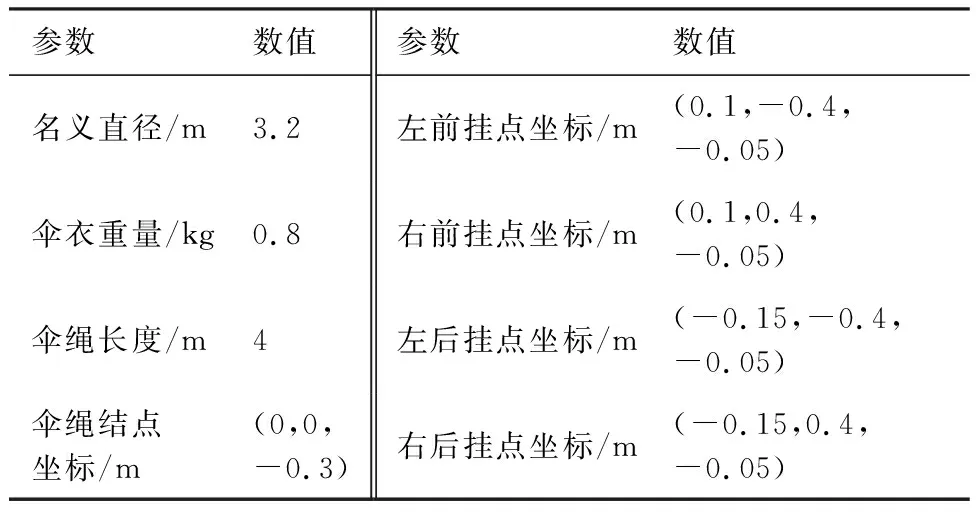
表2 降落伞的主要参数Table 2 Main parameters of parachute

3.2 数字飞行仿真与飞行试验对比

该太阳能无人机在海拔1 360 m、空速15 m/s、 平均风速约5.5 m/s的条件下，从平飞状态开始进行了一次逆风伞降飞行试验(接地点海拔1 300 m)。试验照片如图3所示。飞行试验数据和飞行仿真数据的对比如图4～图15所示。

图3 “魅影”太阳能无人机的伞降飞行试验Fig.3 Parachute landing test of “Mei Ying” UAV

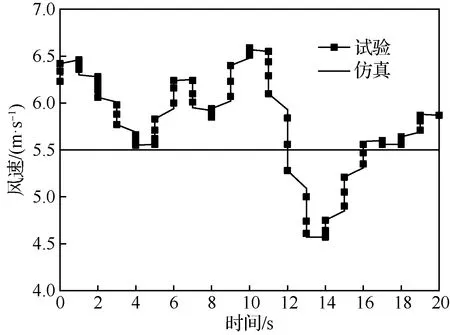
图4 风速Fig.4 Wind speed

由图3可见，该太阳能无人机的伞降过程具有明显的拉直、充气、稳定下降等过程，初始充气阶段的伞形为灯泡状，与半理论半经验的降落伞充气模型的假设一致，因此本文关于伞衣展开过程的简化假设是成立的。

图4为飞行试验中机载传感器记录的风速和飞行仿真所设置的常值风的对比。

由图5和图6可见，飞行仿真中无人机的飞行轨迹和试验值比较接近，由于无人机是逆风着陆，所以在稳定下降阶段飞行轨迹随风向后飘移。

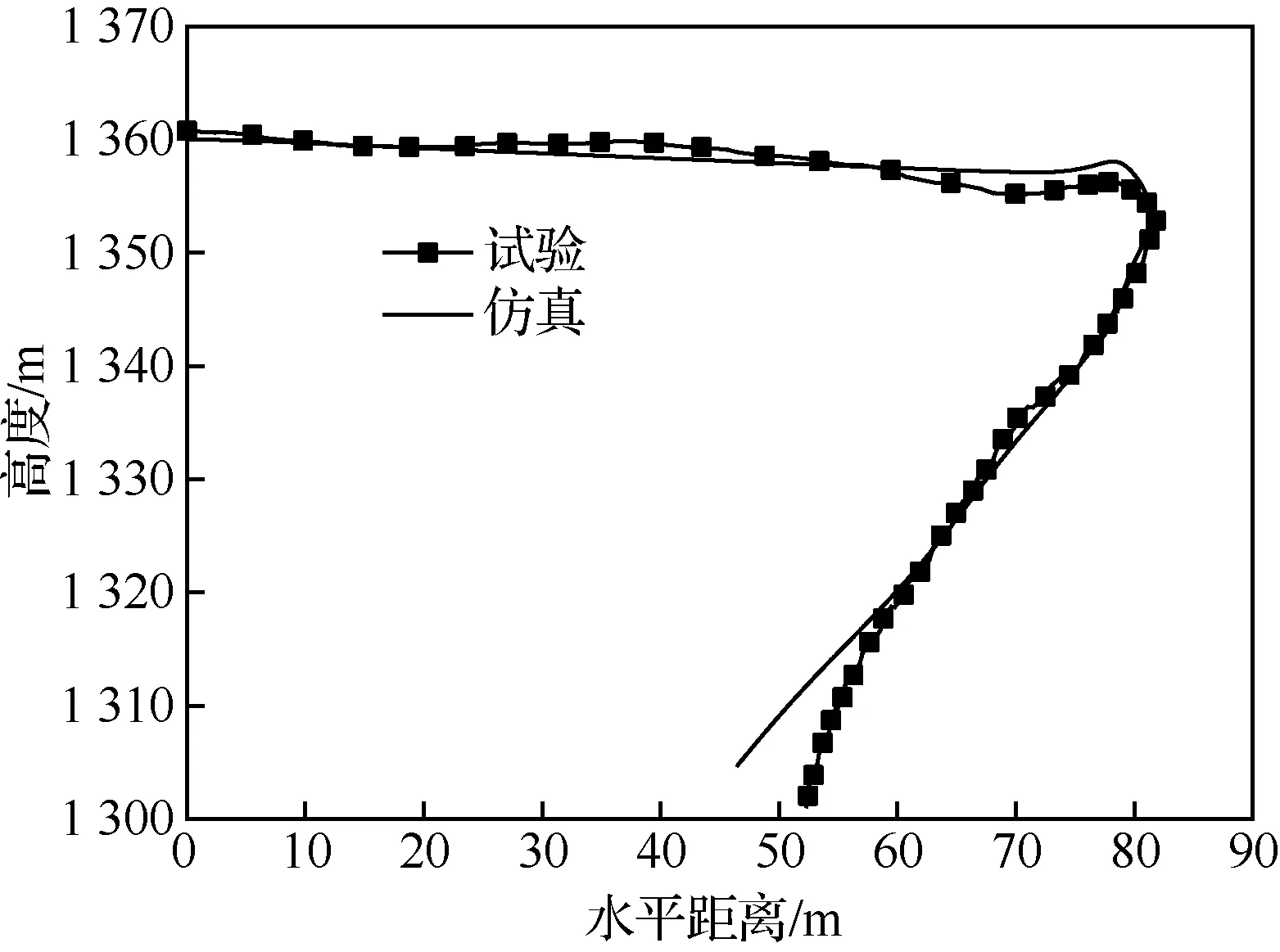
图5 无人机的纵向飞行剖面Fig.5 Longitudinal flight profile of UAV

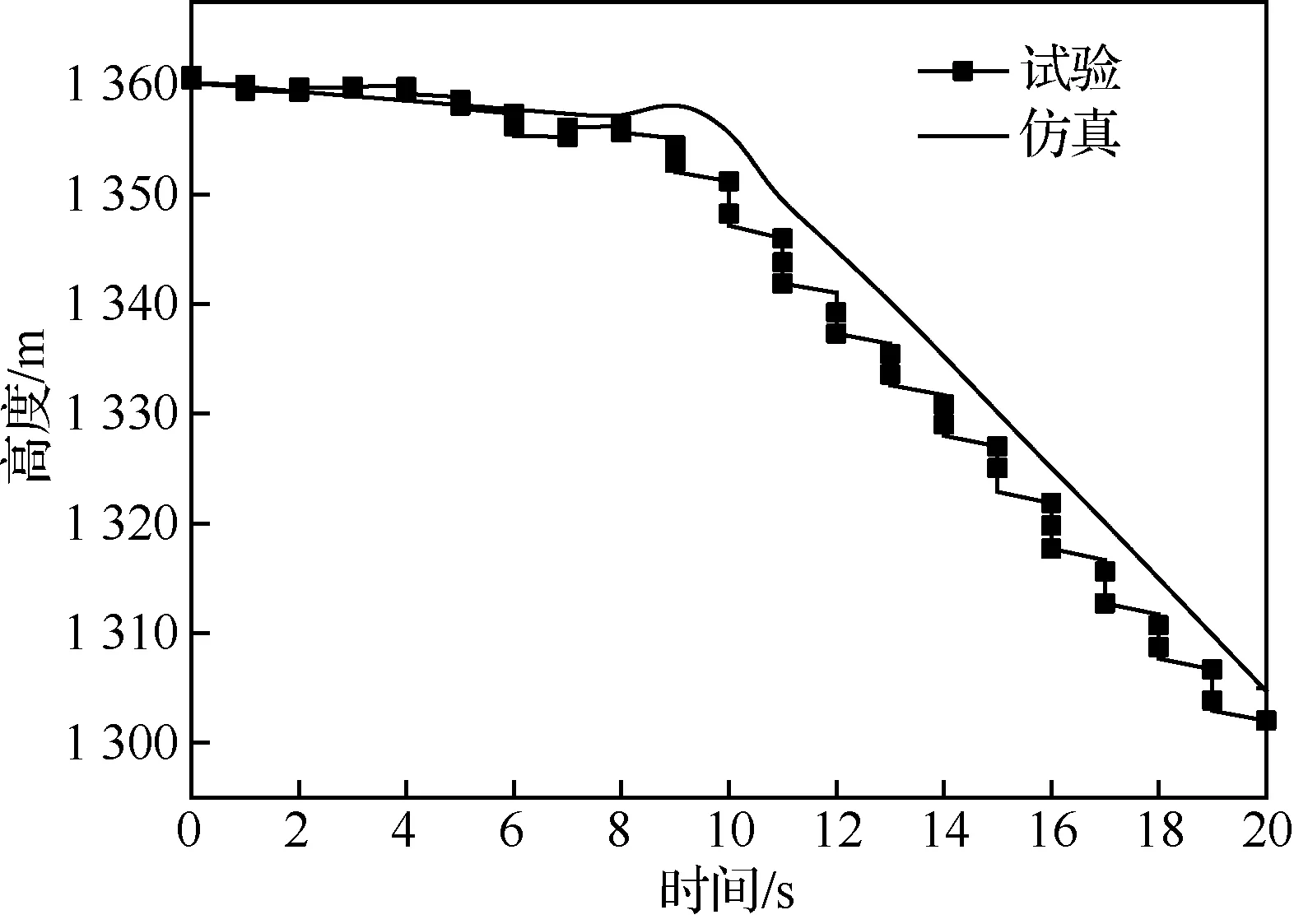
图6 无人机的高度Fig.6 Height of UAV

降落伞抛出之后，在来流的作用下向相对无人机的后上方运动，所以伞绳拉直之后(第7 s左右)对无人机的拉力向后上方。由图7～图9可见，在拉直时刻无人机的下沉速度向上、前飞的空速和地速都有明显的减速，仿真数据与试验数据都能较好地描述了该现象。此外，由图7可见，无人机的稳定下沉速度约为5 m/s，为伞降前的飞行速度15 m/s的1/3，印证了前文所述的太阳能无人机伞降速度与巡航速度差距不如其他类型无人机的描述。

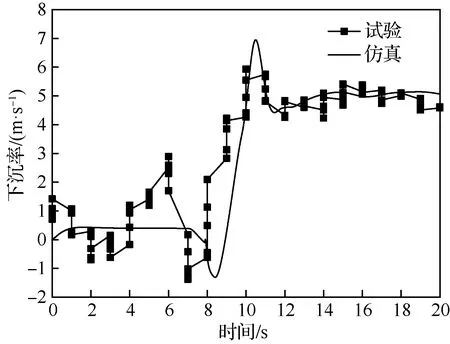
图7 无人机的下沉速度Fig.7 Sink rate of UAV

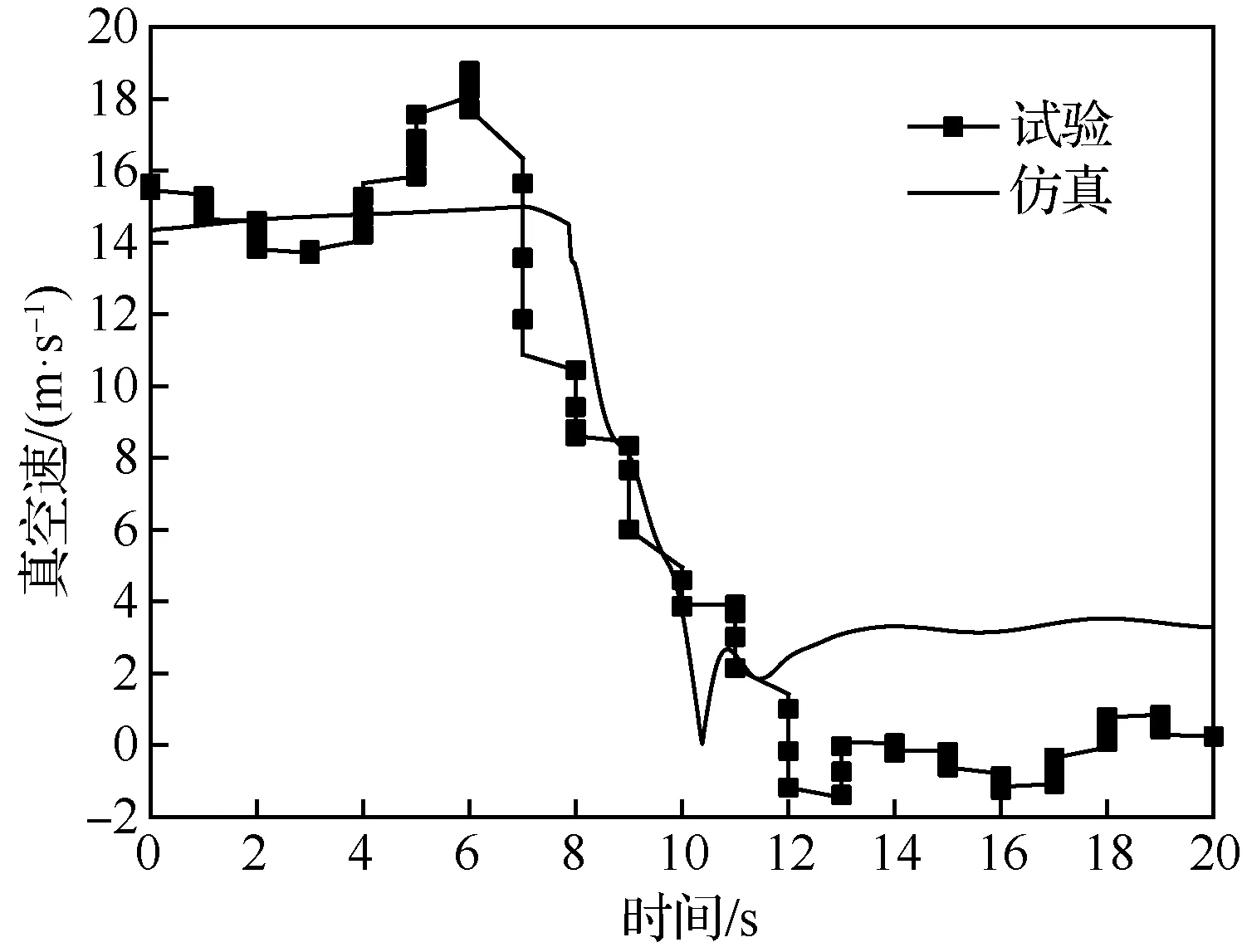
图8 无人机的水平真空速Fig.8 Horizontal true airspeed of UAV

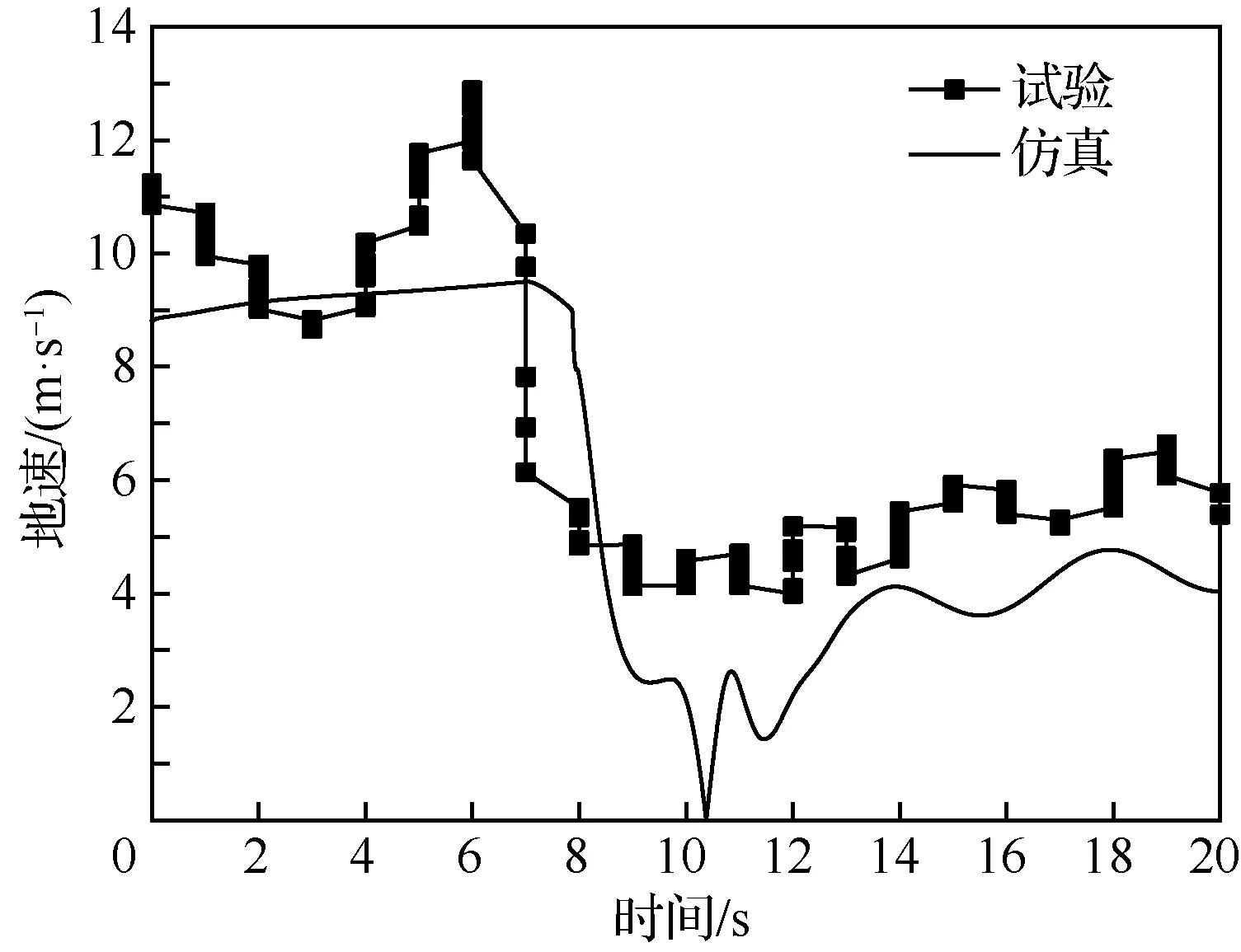
图9 无人机的对地速度Fig.9 Ground speed of UAV

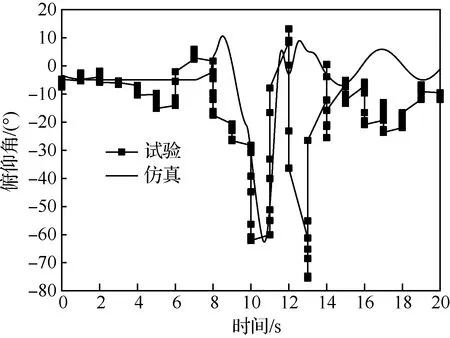
图10 无人机的俯仰角Fig.10 Pitch angle of UAV

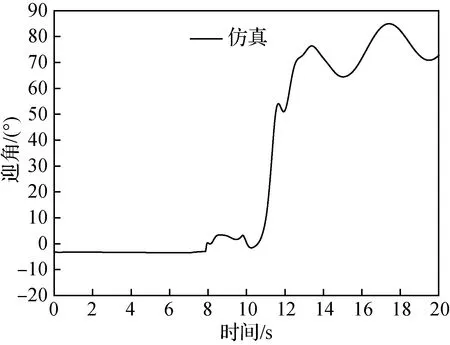
图11 无人机的迎角Fig.11 Angle of attack of UAV

由图10可见，开伞过程无人机的俯仰角振荡比较大，结合图12～图14的仿真数据进行分析，在伞绳刚拉直时，对无人机有一个440 N(约2.5)的拉力，该力的作用点在重心之前，所以会使无人机先抬头、迎角增大(如图11所示)，然后降落伞和无人机在伞绳张力和空气动力的共同作用下，开始进行降落伞向前上方、无人机向后下方的相对转动运动(由图15可见，降落伞的俯仰角在拉直之后从90°逐渐减小到0°附近，说明了降落伞向相对前上方转动)。在无人机抬头且降落伞又逐渐转向相对无人机的上方之后，伞绳拉力的作用点转换到无人机上的后结点(图1中的3、4点)，此时的拉力将使无人机低头，而且在前一阶段大迎角的作用下，到这个阶段无人机在空气动力学俯仰力矩的作用下也将开始低头，于是在这两者的共同作用下无人机的俯仰角减小。当无人机低头到一定程度之后，伞绳拉力的作用点又转移到前结点(图1中的1、2点)，而且到了这时，降落伞的展开面积已经较大(如图14所示)，对无人机的拉力也比前一阶段更大，所以会使无人机以更快的角速度抬头。俯仰角的振荡过程将会持续几次直到伞降过程稳定(伞衣完全张开、伞绳对无人机的拉力作用点变化范围不触及前后结点)之后才会缓解。

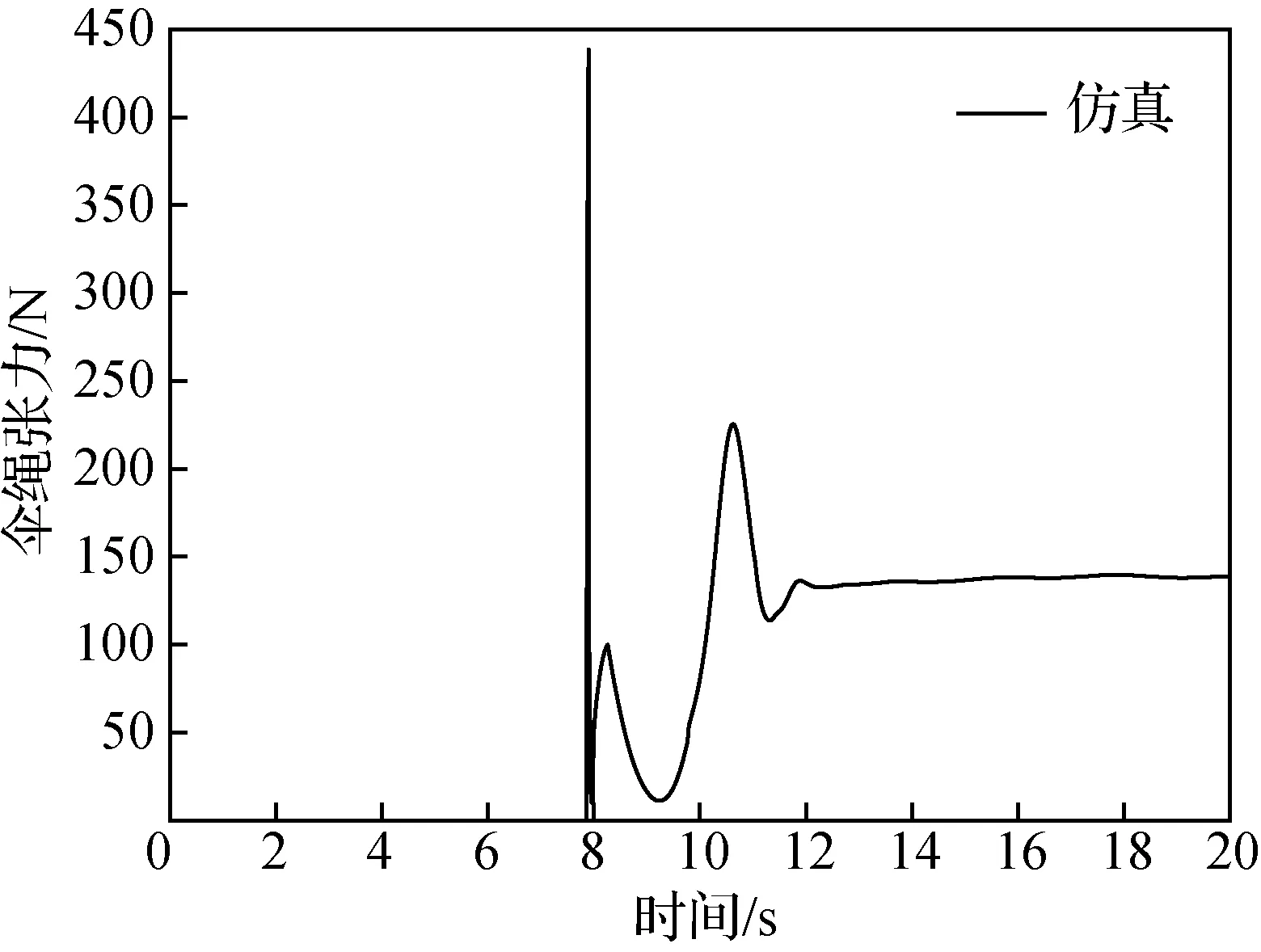
图12 伞绳的张力Fig.12 Tension of parachute rope

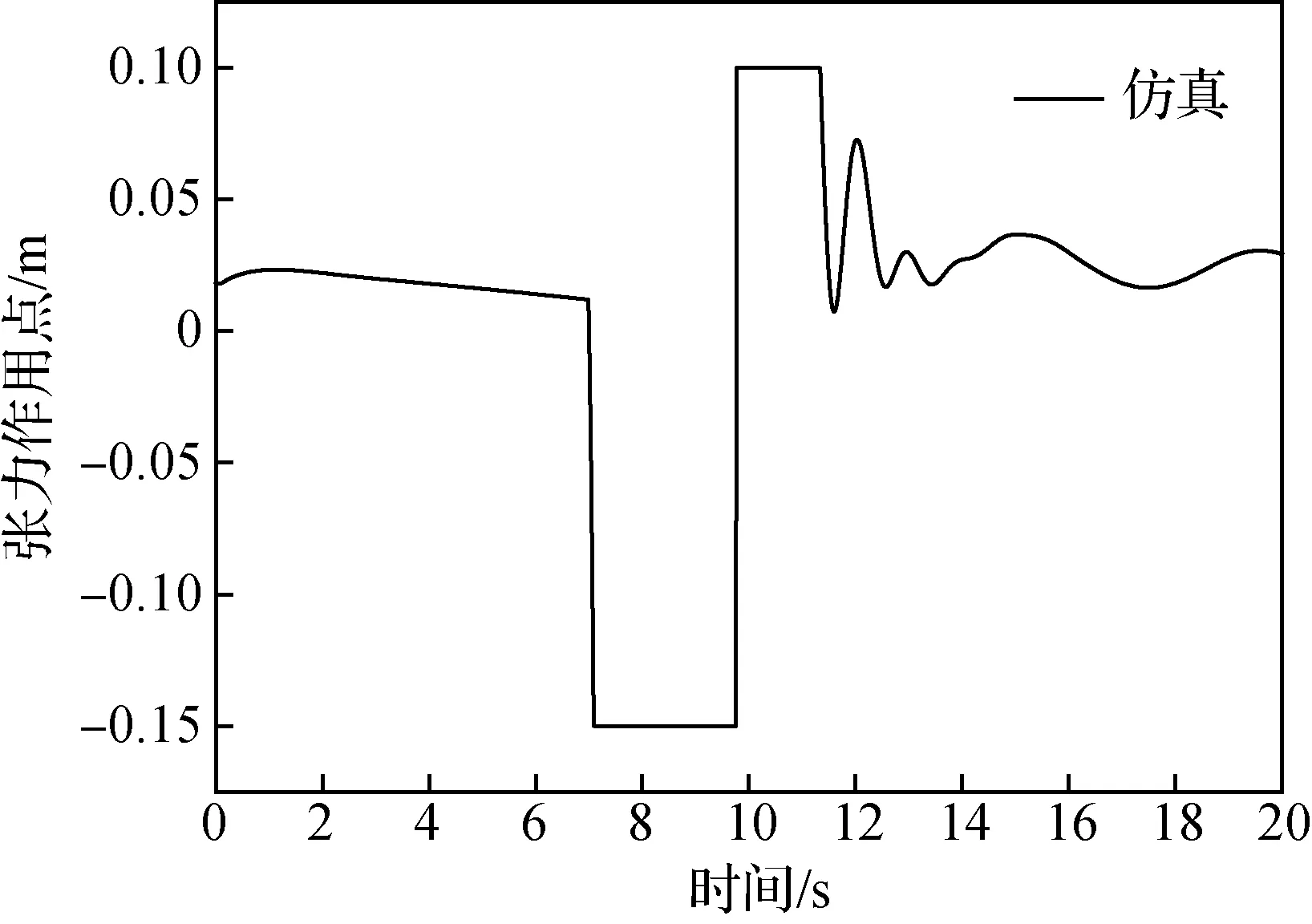
图13 伞绳张力在无人机上的作用点Fig.13 Action point of parachute rope tension on UAV

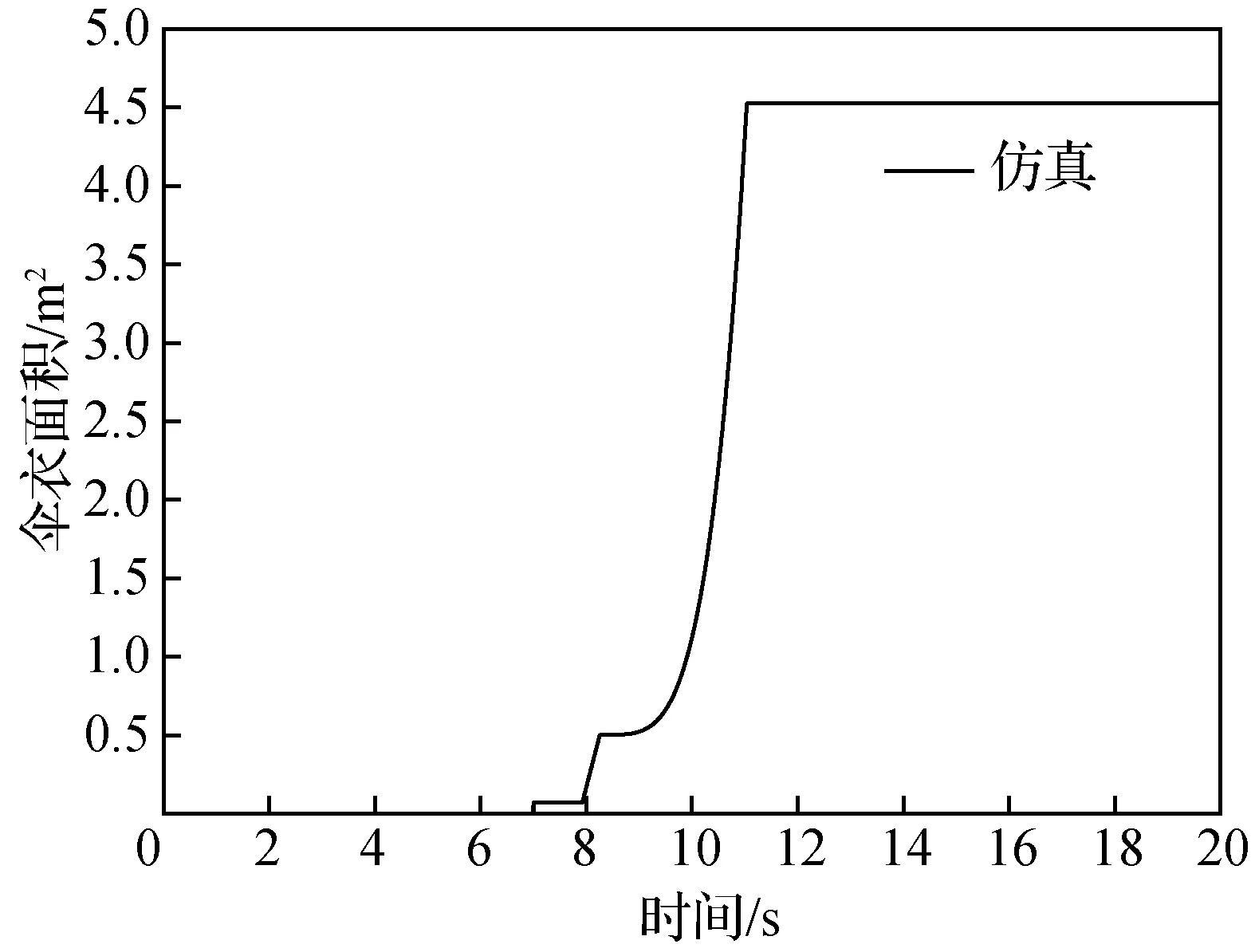
图14 降落伞的伞衣面积Fig.14 Parachute canopy area

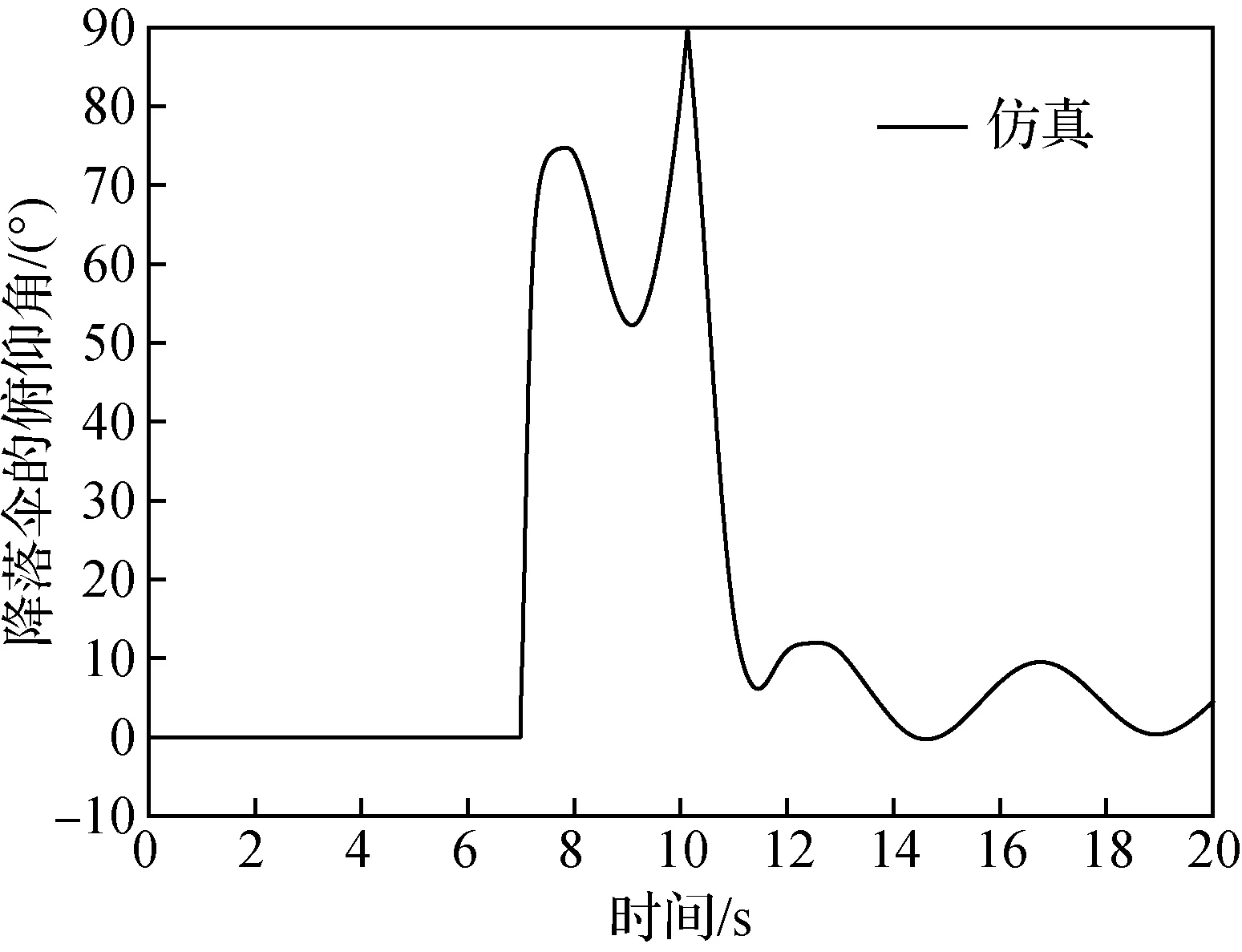
图15 降落伞的俯仰角Fig.15 Pitch angle of parachute

总的来说，该飞行仿真模型较准确地复现了算例太阳能无人机的伞降动力学过程，而且还可以提供更多的飞行试验难以采集的数据，可为伞降的进一步分析和优化提供更多参考。

3.3 参数敏感性分析

为了研究无人机伞降系统的参数敏感性，通过移动伞绳在无人机上的挂点位置进行飞行仿真对比。在原方案的基础上，分别前后移动前挂点和后挂点，移动之后的具体坐标位置如表3所示。其中，因为和方向的坐标不变，所以为了简洁起见，表中仅给出了挂点在机体轴的坐标值。

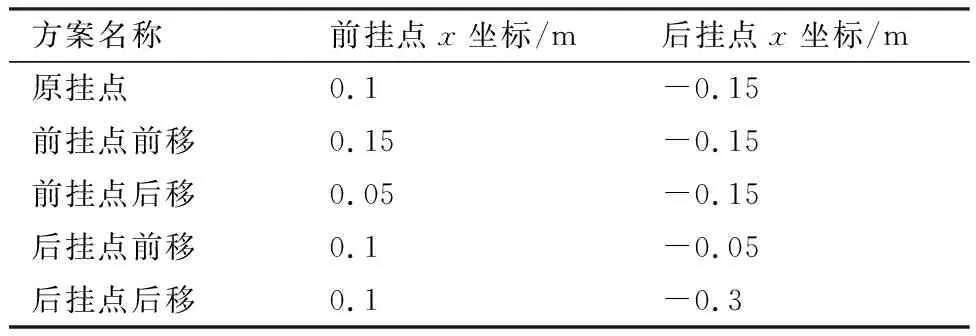
表3 降落伞挂点位置的变换Table 3 Different positions of parachute attachment points

在与上文相同的飞行条件下，降落伞挂点按表3的位置改变之后，采用本文的方法进行伞降飞行仿真的结果如图16～图19所示。

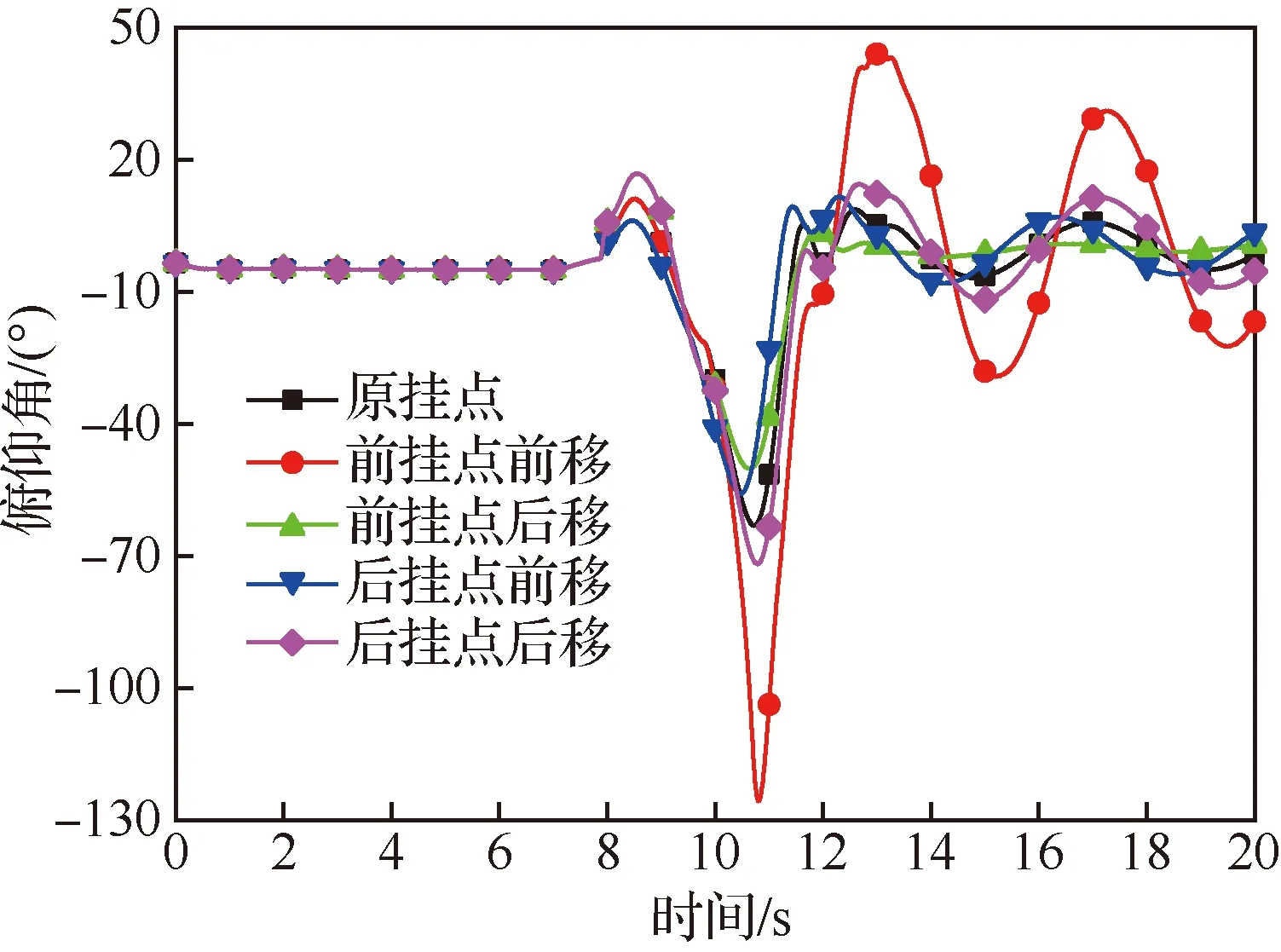
图16 不同挂点下无人机的俯仰角Fig.16 Pitch angle of UAV at different attachment points

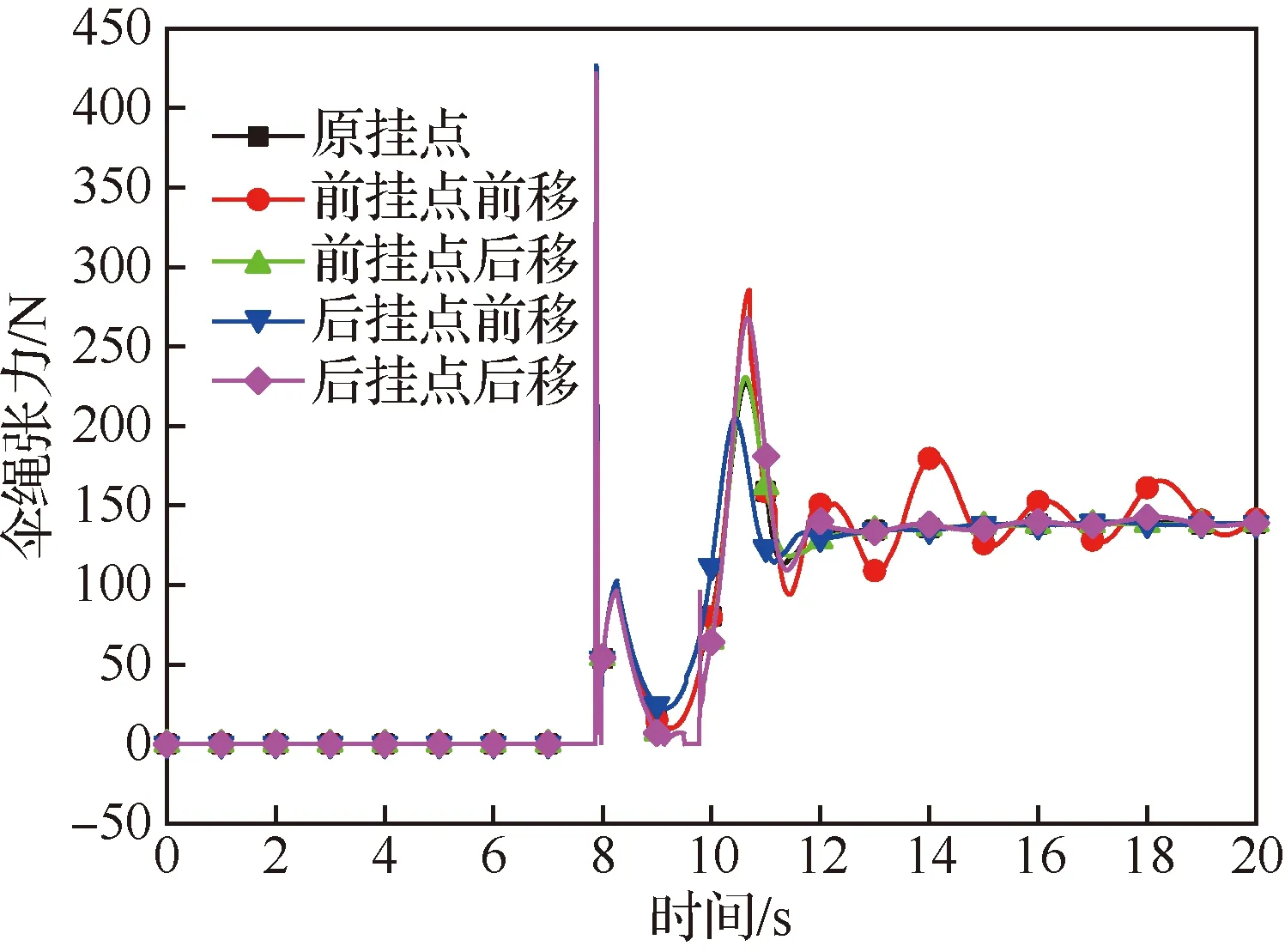
图17 不同挂点下伞绳的张力Fig.17 Tension of parachute rope at different attachment points

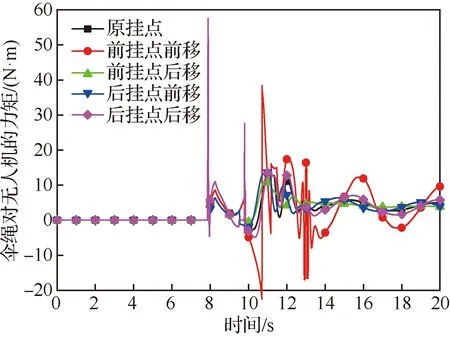
图18 不同挂点下伞绳对无人机的力矩Fig.18 Pitch angle of parachute at different attachment points

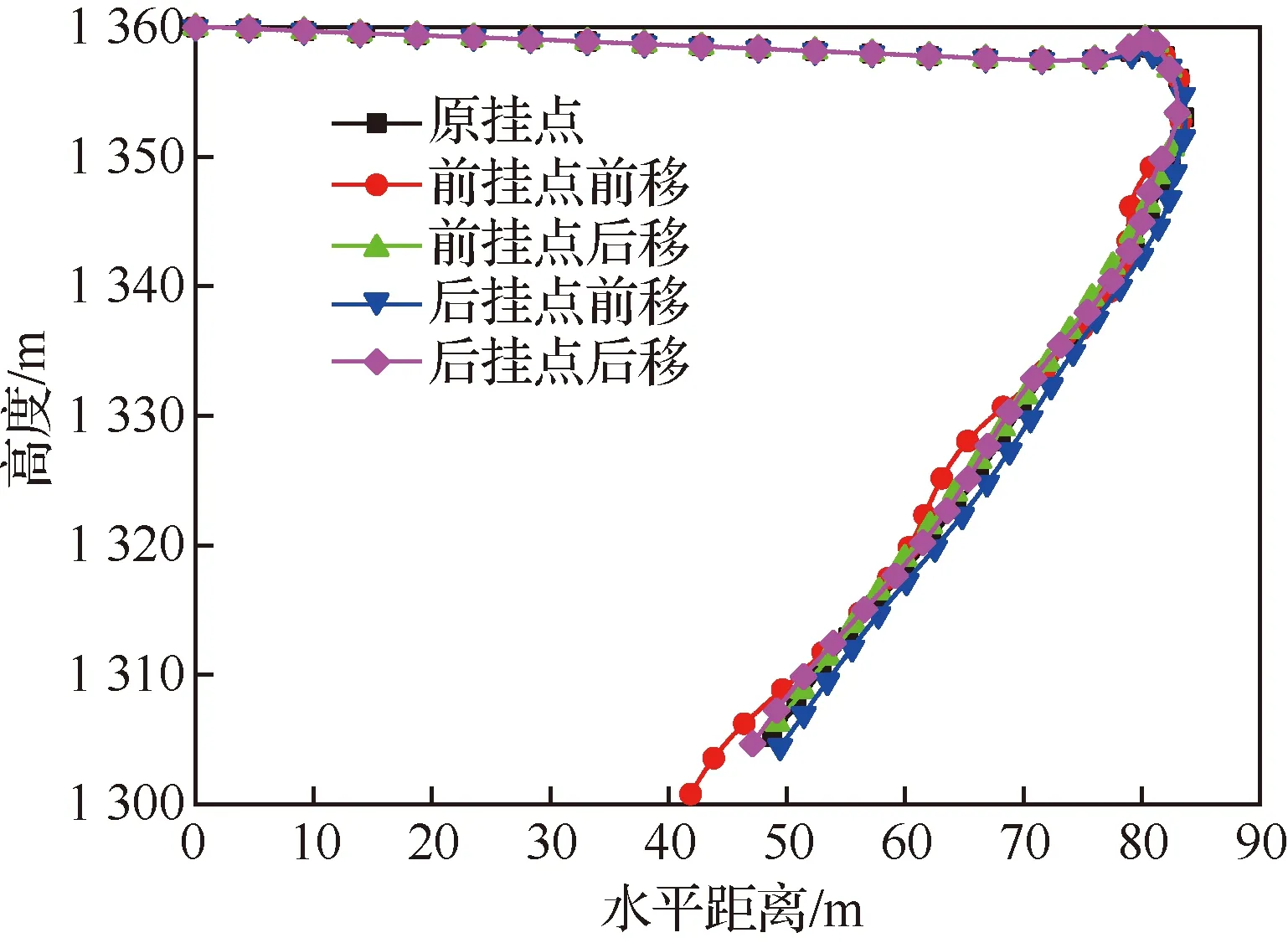
图19 不同挂点下无人机纵向飞行剖面Fig.19 Longitudinal flight profile of UAV at different attachment points

由图16可见，改变伞绳挂点位置后，无人机的俯仰角差异很明显。如果将前伞绳挂点向前移，俯仰角的幅值变化很大；而如果将前伞绳挂点向后移，俯仰角的波动幅值是所对比的5个方案中最小的。从图17和图18来看，在第8～12 s之间，虽然不同方案伞绳的张力差别不大，但是因为挂点的差异，伞绳对无人机的俯仰力矩差别达到了4倍以上，因此带来了较大的俯仰角差异。从图19可见，当把前挂点向前移时，因为俯仰角的波动很大，所以也这个状态的纵向飞行轨迹也是波动最大的，这也说明了在伞降过程中控制无人机的姿态也有利于轨迹的控制。

由图16还可见，伞绳的后挂点前后移动对无人机的姿态影响没有前挂点敏感，这是因为在无人机的伞降过程中，伞绳对无人机的最大冲击载荷是刚绷紧的瞬间，而这时张力的作用点在前挂点，所以前挂点对无人机的扰动力矩影响最大。尤其是对于本算例无人机，由于是飞翼式布局，纵向的稳定性和转动惯量都很小，所以受到大的扰动之后将会维持较长时间的振荡，因此影响更明显。

可以预见，如果将伞绳的前后挂点都移动到重心，降落伞的打开过程对无人机的扰动力矩是最小的(理论上为0)，但是一般并不采用这种吊挂方式。这是因为如果采用前后挂点的方式，由于伞绳的柔性特征，在无人机受到扰动时可以提供更大的稳定力矩：如图17和图18所示，在第11 s左右时无人机有很大的低头，这时后挂点上的伞绳将松弛使得伞绳的力完全作用在前挂点上，因此伞绳对无人机作用有很大的抬头力矩能使之更快速地抬头，从而更快速地恢复到稳定状态。

而且在无人机稳定下沉时，前后挂点的方式也可以平衡无人机的气动力所产生的力矩。由图2的俯仰力矩系数曲线可知，在无人机稳定下降迎角接近90°时，气动力矩欲使无人机低头。在图18的第20 s可见，稳定下降时伞绳因为具有柔性的特性，前后挂点的力不相等，力的等效作用点不过重心，所以对无人机作用有正的抬头力矩，因此可以抵消掉气动力矩的作用，使无人机接地时的姿态角近似为0，从而减小着陆冲击载荷对机体的损坏。

4 结 论

1) 采用本文所建立的忽略了降落伞的自转运动的9自由度伞降模型，对低翼载荷太阳能无人机进行了飞行仿真，仿真结果与飞行试验数据吻合度较高，针对伞绳拉直时无人机有轻微的向上运动的趋势、拉力作用点在前后结点2个极限位置来回切换导致俯仰角振荡明显等细节，均能较好地体现，说明了该模型具有较高的保真度，证明了所提出的无人机伞降着陆多体动力学建模与仿真方法的有效性。

2) 采用参数敏感性分析发现，伞绳在无人机上的前挂点前移对无人机的姿态扰动很大，进而对轨迹和落点的影响也更大，尤其是对本算例的纵向稳定性和转动惯量都很小的飞翼式布局无人机，而后挂点的前后移动对姿态扰动的影响相对不明显。