基于不确定微分方程的疲劳可靠性建模

2022-09-09李晓阳陶昭张慰

航空学报 2022年8期

李晓阳，陶昭，张慰

1.北京航空航天大学可靠性与系统工程学院，北京 100083 2.北京航空航天大学可靠性与环境工程技术国防重点实验室，北京 100083

目前对于疲劳的研究已经取得许多进展，建立起描述疲劳裂纹扩展的模型。通常，疲劳裂纹扩展模型描述裂纹扩展速率与材料、几何形状、载荷等因素的确定性因果关系。然而，在疲劳裂纹扩展过程中，由于材料组织和缺陷的不均匀性、环境条件变化等因素的影响，疲劳裂纹扩展速率会随时间波动，表现出裂纹扩展过程在时间维度的不确定性，并且这种不确定性具有随时间动态变化的特征。即使在控制良好的实验室条件下，疲劳裂纹扩展实验结果中通常也会表现出显著的统计离散性，同样也显示出疲劳规律的统计特性。因此，为了进一步准确认知疲劳裂纹扩展规律，需要从疲劳裂纹扩展的物理机理出发，建立描述疲劳裂纹扩展的理论模型，通过对理论模型输入变量的干预与控制，开展疲劳裂纹扩展实验，验证疲劳裂纹扩展理论模型的正确性，并基于实验数据量化不确定性，从而实现对疲劳裂纹扩展过程的确定性规律的准确认知，以及对时间维度不确定性的动态变化特征的正确量化。

从材料的微观层面来研究疲劳裂纹扩展过程，有位错滑移和热激活引起原子键破裂等物理解释。由于材料微观结构的不均匀性和热涨落的动态性，带来疲劳裂纹扩展过程在时间维度的不确定性的动态变化，宏观层面表现于疲劳裂纹扩展速率随时间波动的统计特性。近40年来，针对疲劳裂纹扩展过程在时间维度的不确定性动态变化开展的建模研究可分为2类：一类是直接利用随机过程来描述疲劳裂纹扩展过程，从而建立疲劳裂纹扩展随机模型；另一类是在疲劳裂纹扩展确定性模型(即基于实验数据的经验模型或基于断裂力学的理论模型)的基础上，引入以随机过程表征的随机因子来建立疲劳裂纹扩展随机模型。直接利用随机过程开展的建模研究中，Bogdanoff和Kozin用马尔可夫链来分析裂纹萌生和扩展中损伤随时间的变化。Hao等基于维纳过程构建出退化模型，并应用于描述疲劳裂纹扩展。这类直接利用随机过程建模的方法，本质上属于统计数据驱动的方法，缺乏对物理过程的描述，从而导致人们对疲劳裂纹扩展的本质认知不清。

而在基于物理机理构建的疲劳裂纹扩展确定性模型基础上，引入随机过程的研究就能较好地解决上述问题。Lin和Yang在疲劳裂纹扩展速率模型中引入一个随机因子来代表未知因素对疲劳裂纹扩展速率随时间变化的综合影响，且考虑相关时间较短时将疲劳裂纹扩展过程视为扩散马尔可夫过程，并以随机微分方程来表示。Li等的研究中引入的随机因子考虑为对数正态随机过程，从而建立起随机疲劳裂纹扩展模型。Sobczyk引入一个非负的随机过程作为随机因子建立了疲劳裂纹扩展随机模型，并分析了该非负随机过程是高斯白噪声时模型的特性。但是高斯白噪声不能解释疲劳裂纹扩展过程的相关性，并且由于其服从高斯分布的特征，而不能满足非负随机因子的条件。对于高斯白噪声的缺陷，研究中引入辅助随机过程，构建疲劳裂纹扩展的两态模型。例如，Spencer等引入辅助随机过程和非负函数构造随机因子，考虑了疲劳裂纹扩展过程的历史依赖性，并以郎之万方程表示引入的辅助随机过程，且郎之万方程中的噪声项为高斯白噪声。高斯白噪声可以视为维纳过程的导数形式dd(维纳过程不可导，本文仅借此导数形式来展开说明)，因此第二类方法构建的疲劳裂纹扩展随机模型可以表示为随机微分方程的形式，这表明随机微分方程可以用于刻画裂纹扩展过程在时间维度的不确定性的动态变化。Allen基于伊藤随机微分方程描述疲劳裂纹扩展过程，其中漂移系数和扩散系数表示为疲劳载荷循环次数的指数函数形式。

上述基于随机微分方程构建的疲劳裂纹扩展随机模型，实际上表征的是每个时间微元d下疲劳裂纹扩展的规律，从小时间尺度(即宏观上相对较小的时间单位，例如1个载荷循环)出发进行建模，并利用动态噪声解释疲劳裂纹扩展过程在时间维度的不确定性的动态变化特征。然而，基于随机微分方程给出的疲劳裂纹扩展速率表达式中动态噪声表示为dd，该项服从正态分布(0,1d)，时间微元d趋近无穷小时方差趋近于无穷大，从而表明疲劳裂纹扩展速率趋近于无穷大，显然与实际认知相违背。在概率理论中，维纳过程用来描述微观粒子的不规则运动(即布朗运动)，可由维纳过程推出时间趋近无穷小时粒子运动速度为无穷大，从微观层面此结论与观测是相符的，然而在宏观层面以维纳过程来描述系统状态变化过程就会出现系统的宏观状态变化速率是无穷大的情况，这与实际认知不符。为了解决这个问题，在不确定理论中以Liu过程描述布朗运动，Liu过程是一个平稳独立增量过程(详见1.1节定义5)。在Liu过程的基础上提出的不确定微分方程中用于表示动态噪声的项为Liu过程的导数形式dd，该项服从正态不确定分布(0,1)，即方差恒为1，避免了随机微分方程在时间微元无穷小时所描述的系统的宏观状态变化速率无穷大的问题。

通过上述调研和分析，本文在不确定理论框架下，考虑疲劳裂纹扩展过程是小时间尺度下损伤的动态累积变化过程，结合疲劳裂纹扩展确定性模型描述疲劳裂纹随时间动态变化的确定性规律，基于不确定微分方程描述时间维度的不确定性的动态变化特征；此外，本文还考虑物理属性、外界载荷和裂纹阈值3个方面由于实验数据量有限带来的认知不确定性，这些不确定性具有静态特征，并基于不确定分布进行量化；进而，构建出小时间尺度下基于不确定微分方程的疲劳裂纹扩展模型，并推导出确信可靠度函数。

1 不确定理论与疲劳裂纹扩展模型概述

本节介绍不确定理论的相关概念，以及描述疲劳裂纹扩展确定性规律的模型，作为本文理论建模的基础。

1.1 不确定理论的相关概念

本节主要介绍一些不确定理论的基础知识以及本文中用到的定义定理等。

考虑一个非空集合，将集合上的-代数记为L，L中的每个元素是一个事件，则不确定测度M是一个满足以下4个公理的从到[0,1]的集函数：

(规范性)对于全集，M{}=1。

(对偶性)∀∈L，M{}+M{}=1，式中：为的补集。

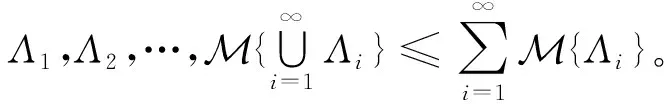
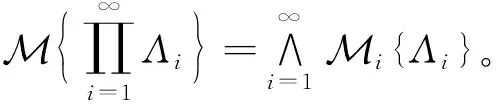
不确定变量是一个从不确定空间(,L，M)到实数集的函数，即对于任意的Borel集，{∈}是一个事件。

不确定变量的不确定分布定义为()=M{≤}，其中为任意实数。相应地，反函数()是不确定变量的逆不确定分布，其中为信度。

对于正态不确定变量，定义其不确定分布形式为

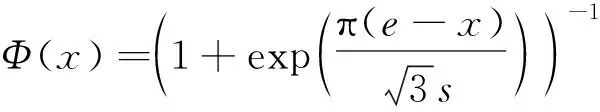
(1)

式中：为期望；为标准差，>0。将满足式(1)的不确定分布记为(,)，相应的逆不确定分布形式为

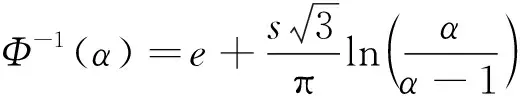
(2)

对于相互独立的不确定变量,,…,，其不确定分布分别为,,…,，连续函数(,,…,)关于,,…,严格递增且关于+1,+2,…,严格递减，则不确定变量=(,,…,)的逆不确定分布为

(3)

对于不确定变量和正整数，的阶矩表示为

(4)

对于不确定空间(,L，M)和全序集(如时间)，不确定过程是一个从×(,L，M)到实数集的函数，即不确定过程在任意时刻都是一个不确定变量。Liu过程是一个满足以下3个条件的不确定过程：①=0且几乎所有的样本轨道都是Lipschitz连续的；②具有平稳独立增量；③ 每个增量+Δ-是期望为0，方差为(Δ)的正态不确定变量。

对于给定的函数、和一个Liu过程，不确定微分方程表示为

d=(,)d+(,)d

(5)

在任意时刻满足该方程的不确定过程称为该不确定微分方程的解。

1.2 考虑裂纹闭合和高载迟滞效应的疲劳裂纹扩展模型

本节介绍描述疲劳裂纹扩展确定性规律的模型，这些模型考虑了裂纹闭合和高载迟滞效应对裂纹扩展过程的影响。本节仅给出本文理论建模中所必需的模型表达式，关于模型的具体建模过程可参考文献[19]。

考虑裂纹闭合对裂纹扩展过程的影响，疲劳裂纹扩展速率表示为

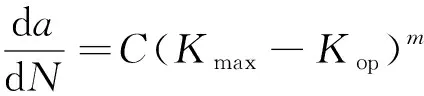
(6)

式中：为裂纹长度；为载荷循环次数；d/d为裂纹扩展速率；和为与材料相关的参数；为最大应力强度因子；为裂纹闭合时的应力强度因子；为应力强度因子。在疲劳裂纹扩展实验中，通常的计算公式由相应的试验标准给出。例如在GB/T 6398—2017中，对于如图1所示中心裂纹拉伸试样，的计算公式为

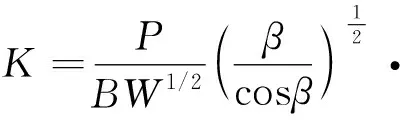
(0707 1-0007 2+0007 0)

(7)

式中：为中间变量，且=π(2)；为载荷，与应力可以相互转化；和分别为样件的厚度和宽度。因此，本文将给定试样几何尺寸时应力强度因子表达式统一记为=(,,,)，其中表示函数，那么式(6)可以写为

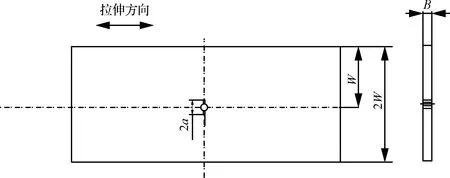
图1 中心裂纹拉伸试样(2W≤75 mm)Fig.1 Center cracked tension specimen (2W≤75 mm)

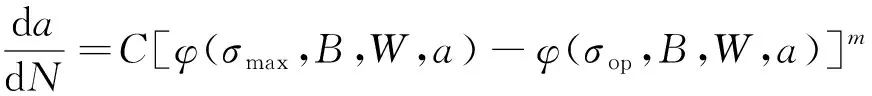
(8)

式中：为最大应力水平；为裂纹闭合应力水平。

对于裂纹闭合应力水平的研究，Zhang和Liu通过考虑裂纹尖端塑性区与裂纹扩展过程的关系，给出下列计算公式：

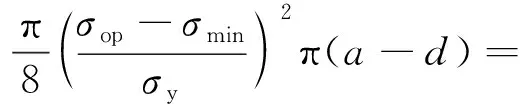
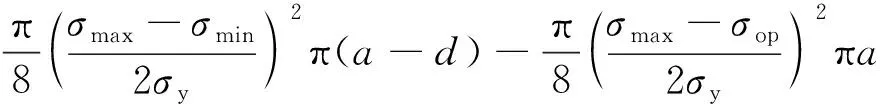
(9)

式中：为材料的屈服应力；为加载过程中的正向塑性区尺寸；和分别为最大应力水平和最小应力水平。在Zhang和Liu的研究中考虑裂纹尖端塑性区尺寸远小于裂纹长度，即≪，对于恒幅载荷加载的疲劳裂纹扩展过程，易解得=(2+3)/5。

考虑高载引起的迟滞效应，最大应力水平表示为

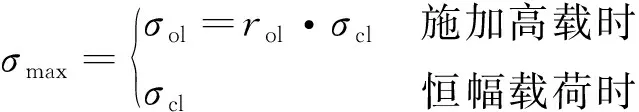
(10)

式中：为高载幅值；为恒幅载荷的最大应力水平；为过载比，即与的比值。

2 疲劳可靠性建模方法

2.1 基于不确定微分方程的疲劳可靠性模型

2.1.1 小时间尺度下基于不确定微分方程的疲劳裂纹扩展模型

疲劳裂纹扩展过程是小时间尺度下损伤随时间的累积变化过程，裂纹长度随时间增长呈现出确定性趋势，同时也伴随着时间维度的不确定性。疲劳裂纹扩展过程是确定性趋势和不确定性的综合体现，同时确定性趋势和不确定性在该过程中都是动态变化的。因此，对疲劳裂纹扩展过程的建模需要综合考虑小时间尺度下的确定性趋势和不确定性的动态变化特征。

小时间尺度下通常以疲劳裂纹扩展速率来描述疲劳裂纹扩展过程，本文以疲劳裂纹扩展速率式(8)来表征疲劳裂纹扩展的确定性趋势，在此基础上考虑疲劳裂纹扩展速率加上动态噪声来解释不确定性的动态变化。在不确定理论框架下，本文假设该动态噪声项为·dd，其中常数为扩散系数，且>0；为Liu过程，服从正态不确定分布(0,)；为累积载荷循环次数。因此，小时间尺度下描述疲劳裂纹扩展过程的确定性趋势以及不确定性的动态变化特征的方程为

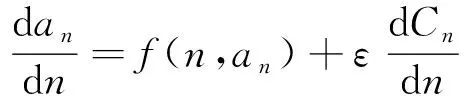
(11)

式中：为累积载荷循环次数为时的裂纹长度，初始裂纹长度为；函数(,)为疲劳裂纹扩展速率，表达式如式(8)所示。进一步，将式(11) 表示为不确定微分方程的形式：

d=[(,,,)-

(,,,)]d+d

(12)

如引言所述，样件自身物理属性、外界载荷和裂纹阈值3个方面也存在不确定性，并且这些不确定性具有静态特征。本文将基于文献[19]对相关参数进行分类和量化，具体将从如下3个方面展开说明：

1) 在物理属性方面。当样件数量有限时带来物理属性的认知不确定性。假设物理属性的不确定性仅来源于材料特性。式(6)在描述疲劳裂纹扩展时，和都代表与材料相关的参数，如果我们认为和都是具有不确定性，那么多个材料参数就需要对应多个不确定性来源，而显然当前只有材料特性这一个来源。所以，只需用和的其中一个来表征这类不确定性即可。根据文献[19，23]中基于实际数据得到的材料参数和的估计结果，可以发现通常的变异系数相比更大，表明的分散性更加显著。因此，本文以材料参数来刻画物理属性方面的不确定性，并假设材料参数服从期望为，标准差为的正态不确定分布(,)，其分布形式如式(1)所示。

2) 在外界载荷方面。本文考虑与高载信息相关的实验数据不足带来的认知不确定性，假设高载施加的条件是确定的，高载幅值具有不确定性，这种不确定性可以用过载比来刻画。因此，假设过载比服从期望为、标准差为的正态不确定分布(,)，其分布形式如式(1)所示。

3) 在裂纹阈值方面。以裂纹长度为性能参数，对应的阈值即为临界裂纹长度，临界裂纹长度表示材料断裂时的裂纹长度，记为。当样件数量有限时带来临界裂纹长度的认知不确定性，本文假设其服从期望为、标准差为的正态不确定分布(,)，其分布形式如式(1)所示。

综上所述，式(12)对于疲劳裂纹扩展过程的确定性趋势和不确定性的动态变化特征进行了量化描述，同时正态不确定分布(,)、(,)和(,)分别对物理属性、外界载荷和裂纹阈值3个方面的认知不确定性的静态特征进行了量化描述，从而构建出小时间尺度下基于不确定微分方程的疲劳裂纹扩展模型。

2.1.2 确信可靠度函数

在确信可靠性理论中，可靠度被定义为产品裕量大于0的可能性。首先，确信可靠度和常规可靠度都是严格遵循可靠度的基本定义的，即规定条件下规定时间内产品完成规定功能的能力。然而，常规可靠度并不区分随机不确定性和认知不确定性(比如小样本带来的认知不确定性)，均将可靠性定义中的“能力”定义为概率。而确信可靠性理论对随机和认知2类不确定性进行了区分，随机不确定性情况下可靠度仍然采用概率度量，而小样本认知不确定性情况下，由不确定测度度量。

在确信可靠性理论中，为了推导疲劳确信可靠度函数，首先需要建立裕量方程(该方程也即机械、力学领域普遍的极限状态方程)。本文以裂纹长度作为性能参数，临界裂纹长度作为阈值，则疲劳裂纹扩展的裕量定义为临界裂纹长度与当前裂纹长度的距离，即裂纹裕量方程表示为

(13)

式中：为裂纹裕量；为临界裂纹长度；为当前累积载荷循环次数为时的裂纹长度。

式(8)～式(10)描述了疲劳裂纹扩展的确定性规律，随着的增加，当前裂纹长度增加，对应的裂纹裕量减小。式(12)以及(,)、(,)和(,)则表征了疲劳裂纹扩展过程中不确定性的量化结果，即材料参数、过载比、临界裂纹长度以及裂纹扩展过程在时间维度的动态变化均存在不确定性，且均采用不确定测度进行量化。因此，根据式(13)可知，裂纹裕量也是一个不确定变量，且相应的疲劳确信可靠度定义为裂纹裕量大于0的信度。当样件给定时，裂纹裕量与恒幅载荷的最大应力水平和累积载荷循环次数有关，则将裂纹裕量记为(,)，其不确定分布记为()。那么确信可靠度函数的表达式为

(,)=M{(,)>0}=1-(0)

(14)

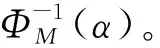
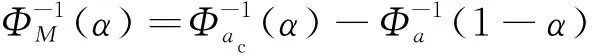
(15)

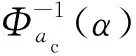
设满足式(12)所示不确定微分方程的解为=(,,)，即表示为材料参数、过载比和Liu过程的函数，的函数形式由式(9)、式(10)和式(12)唯一确定。通过附录A的分析得到，(,,)关于材料参数和Liu过程严格递增，关于过载比严格递减，因此根据定理1得到

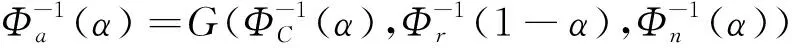
(16)

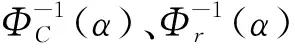
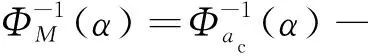
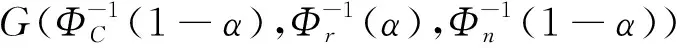
(17)

2.2 统计分析方法

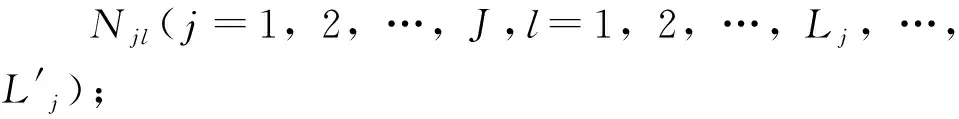
基于不确定微分方程的广义矩估计方法，根据每个样件施加高载前的裂纹长度和对应的载荷循环次数估计未知参数{,,,}。

1) 根据式(18)计算变量(=1, 2, …,;=1, 2, …,-1)，该变量服从正态不确定分布(0,1)。

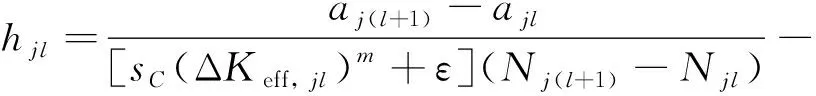
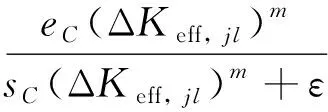
(18)

式中：Δ,为第个样件第次检测的裂纹长度对应的有效应力强度因子范围，且有效应力强度因子范围Δ表达式为Δ=-。施加高载前裂纹在恒幅载荷下扩展，此时Δ,计算公式为

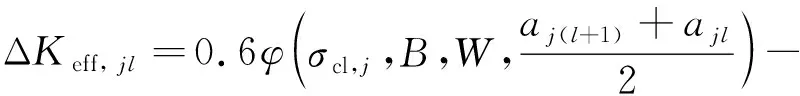
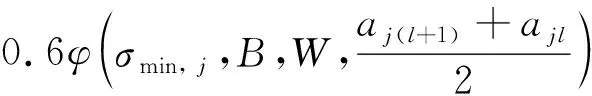
(19)

2) 根据式(20)计算不确定变量的阶矩(=1, 2, 3, 4)。

(20)

3) 求解如下问题的最优解，得到未知参数{,,,}的广义矩估计。

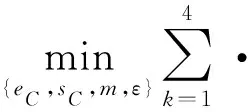
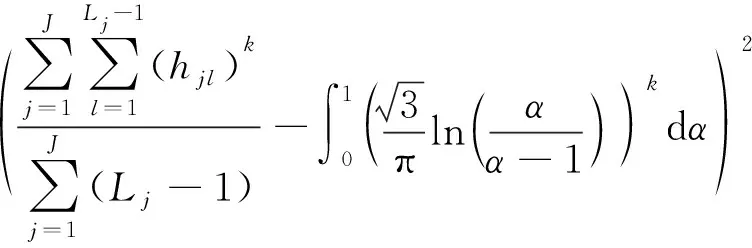
(21)

基于不确定最小二乘方法，根据高载幅值数据估计未知参数{,}。

1) 计算过载比ol,：

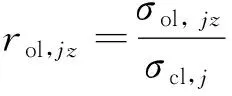
(22)

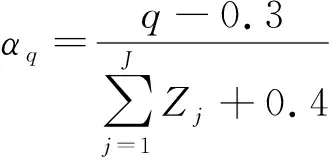
(23)

3) 基于最小二乘原理，求解如下问题的最优解，得到未知参数{,}的估计值。

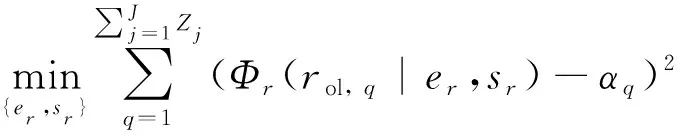
(24)

基于不确定最小二乘方法，根据临界裂纹长度数据估计未知参数{,}。

1) 将样件断裂前最后一次检测时的裂纹长度′(=1, 2, …,)作为临界裂纹长度，然后将′按照升序排列得到(为秩次，=1, 2, …,)，并依据近似中位秩公式给定信度：

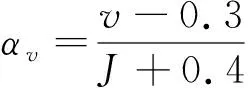
(25)

2) 基于最小二乘原理，求解如下问题的最优解，得到未知参数{,}的估计值。

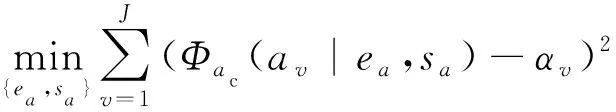
(26)

3 疲劳裂纹扩展实验及模型应用分析

3.1 7075-T6铝合金疲劳裂纹扩展实验

3.1.1 实验设置及实验数据

本案例的数据来源于采用7075-T6铝合金开展的疲劳裂纹扩展实验，实验中5个样件的尺寸如图2所示，样件的载荷谱以及详细的载荷信息分别如图3和表1所示，在裂纹长度达到17.5 mm和22.5 mm时分别施加高载。表示恒幅载荷最大值，表示恒幅载荷最小值，表示裂纹长度17.5 mm时的高载幅值，表示裂纹长度22.5 mm时的高载幅值。实验设计中包含3个应力水平，每个应力下2个样件，但是恒幅载荷最大值20 kN下的另一个样件由于应力加载方式存在缺陷造成数据结果不合理，因此20 kN下只得到一个样件的实验结果，这也是本文采用不确定理论解决此类小样本问题的原因。

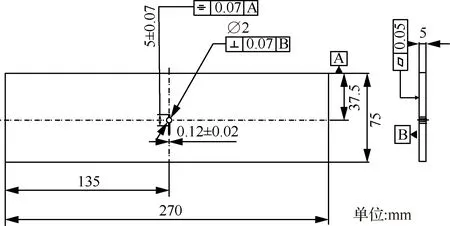
图2 样件几何尺寸Fig.2 Geometry of components

图3 疲劳裂纹扩展实验载荷谱示意图Fig.3 Illustration of loading spectrum of fatigue crack growth experiment

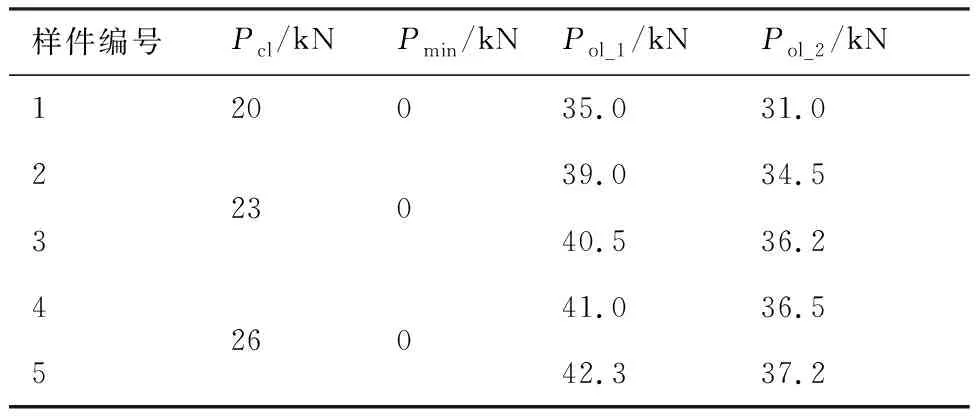
表1 7075-T6铝合金疲劳裂纹扩展实验载荷大小

实验中采用读数显微镜监测裂纹长度，分度值为0.01 mm，并且在数据采集过程中使用安装在显微镜上的叉丝作为参考线。疲劳裂纹扩展实验(FCGE)中记录了裂纹长度和对应的载荷循环次数，数据如图4所示。另外，将每个样件断裂前最后一次检测时的裂纹长度作为临界裂纹长度，如表2所示。

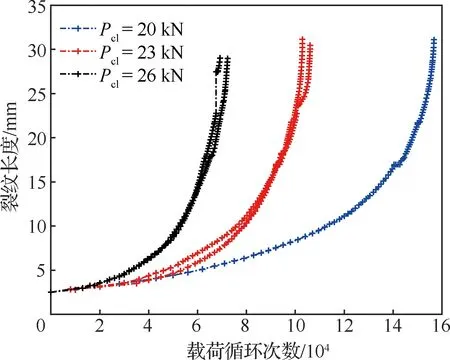
图4 7075-T6铝合金疲劳裂纹扩展实验的裂纹长度与载荷循环次数Fig.4 Crack length and number of load cycles of FCGE with aluminium alloy 7075-T6

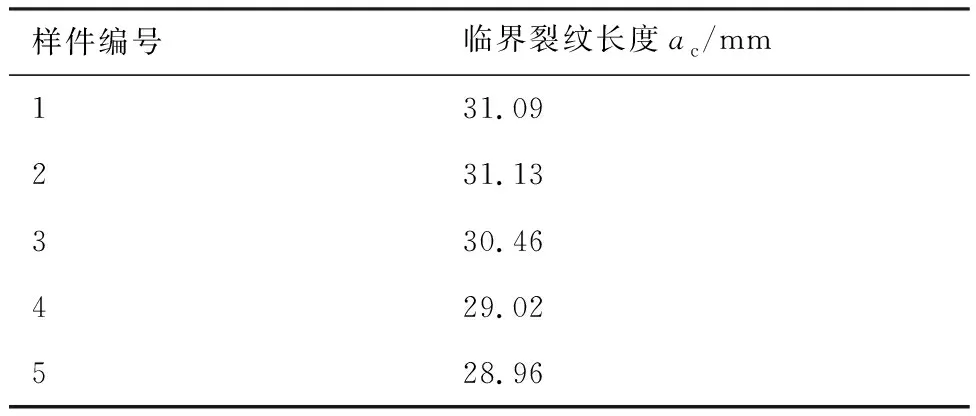
表2 样件的临界裂纹长度Table 2 Critical crack length of components

3.1.2 参数估计结果及确信可靠度评估结果

对于本案例的实验数据，将图4中每个样件施加高载前的裂纹长度和对应的载荷循环次数，表1中恒幅载荷幅值和高载幅值，以及表2中临界裂纹长度作为统计分析的输入数据，然后按照2.2节统计分析方法，得到未知参数的估计结果如表3所示。

表3 未知参数估计结果Table 3 Estimation results of unknown parameters

同时，给出不确定变量、过载比和临界裂纹长度的分布拟合结果，分别如图5～图7所示，从图中可以发现不确定变量、过载比和临界裂纹长度的信度计算值和各自相应的正态不确定分布接近，说明了未知参数估计结果的准确性。另外，不确定变量服从正态不确定分布的推论与材料参数服从正态不确定分布的假设有直接联系，根据文献[26]中的分布假设检验方法，结合图5～图7所示分布拟合结果，材料参数、过载比和临界裂纹长度服从正态不确定分布通过假设检验，验证了2.1节建模方法中模型假设的合理性。

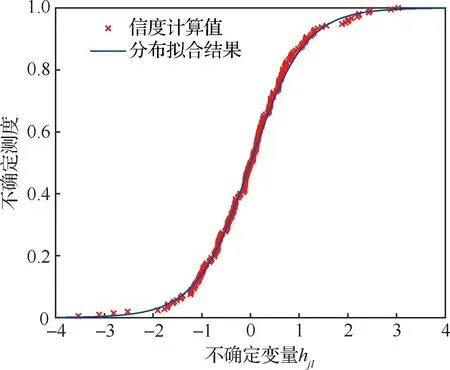
图5 不确定变量hjl的分布拟合结果Fig.5 Fit result of uncertainty distribution of uncertain variable hjl

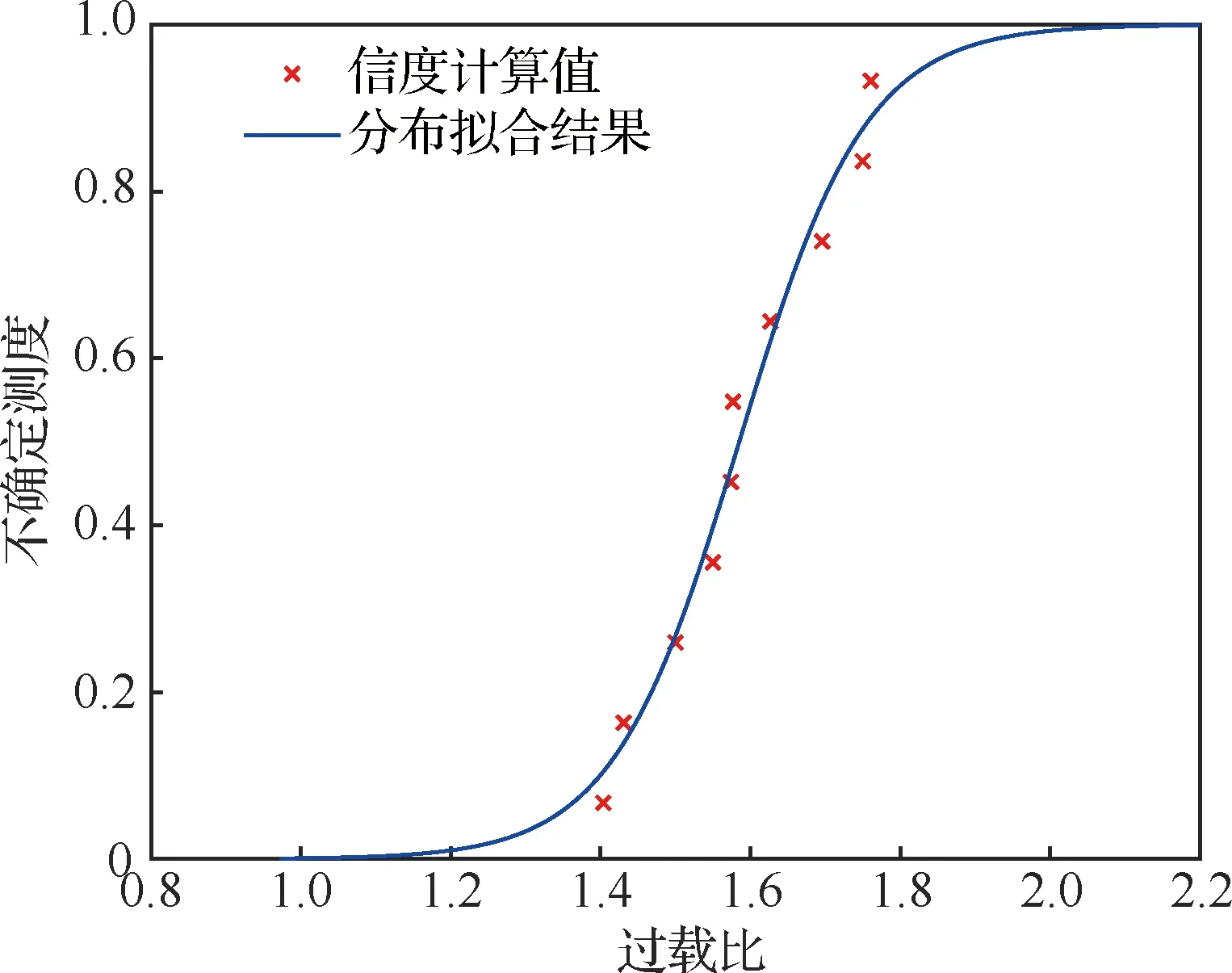
图6 过载比的分布拟合结果Fig.6 Fit result of uncertainty distribution of overload ratio

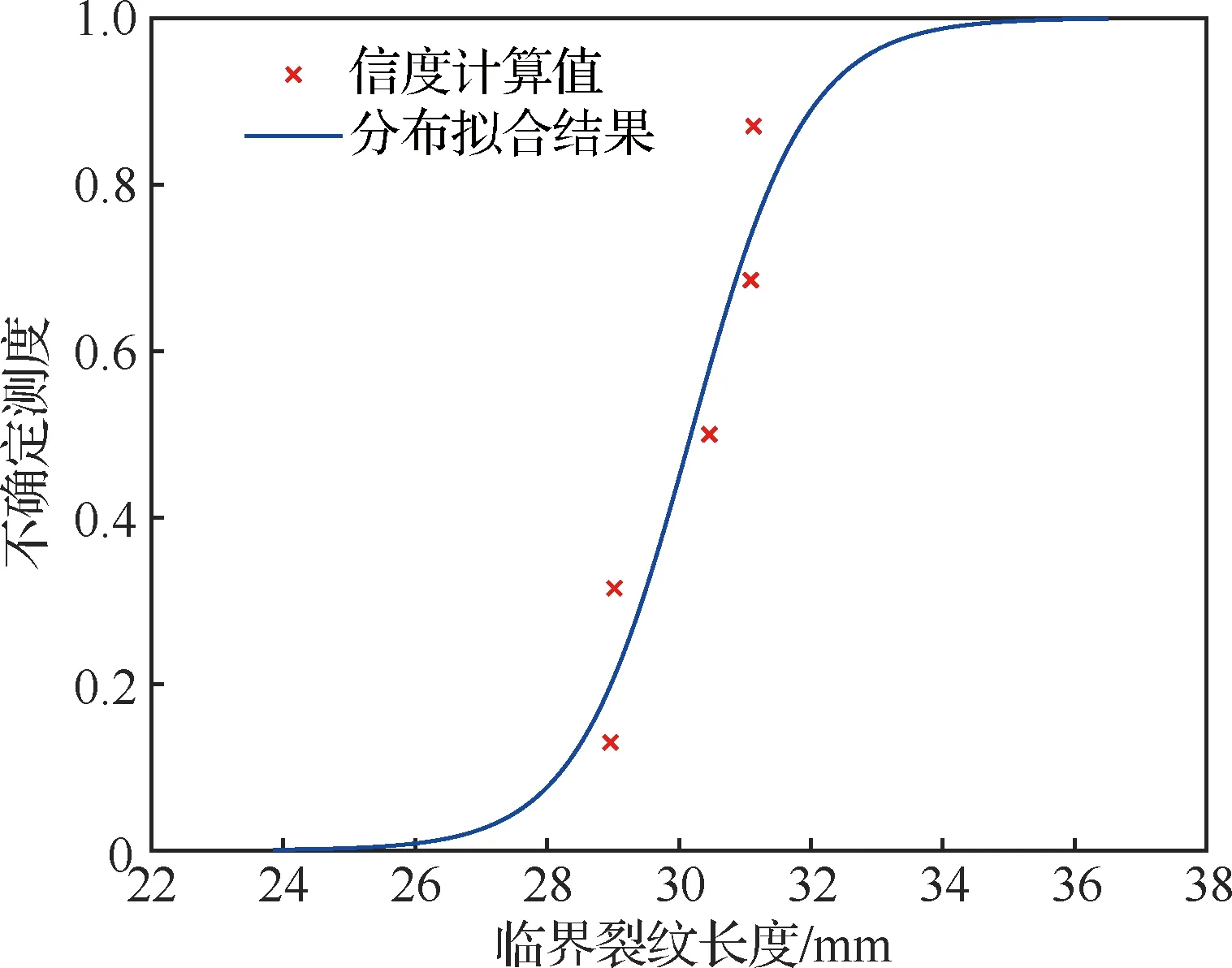
图7 临界裂纹长度的分布拟合结果Fig.7 Fit result of uncertainty distribution of critical crack length

根据参数估计结果和确信可靠度函数式(14)，计算确信可靠度随恒幅载荷最大值和载荷循环次数的变化关系，结果如图8所示。

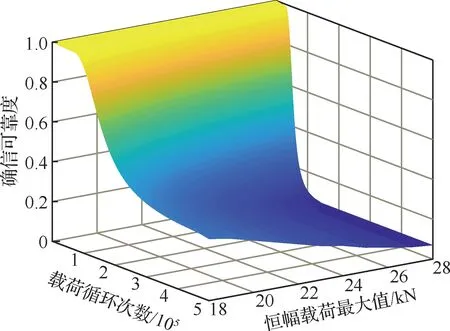
图8 7075-T6铝合金试样的确信可靠度评估结果Fig.8 Result of belief reliability evaluation of specimens with taluminium alloy 7075-T6

3.1.3 裂纹扩展过程确定性趋势预测

为了预测裂纹扩展的确定性趋势，以表3中不确定变量的期望,,分别代表不确定变量、和，结合式(8)～式(10)预测恒幅载荷最大值分别为20 kN、23 kN和26 kN时的裂纹扩展过程的确定性趋势。预测结果如图9所示，在图中同时展示了实验数据。从图中可以看出，预测结果和实验数据比较接近，说明本文提出的模型对于疲劳裂纹扩展确定性趋势的预测较准确。

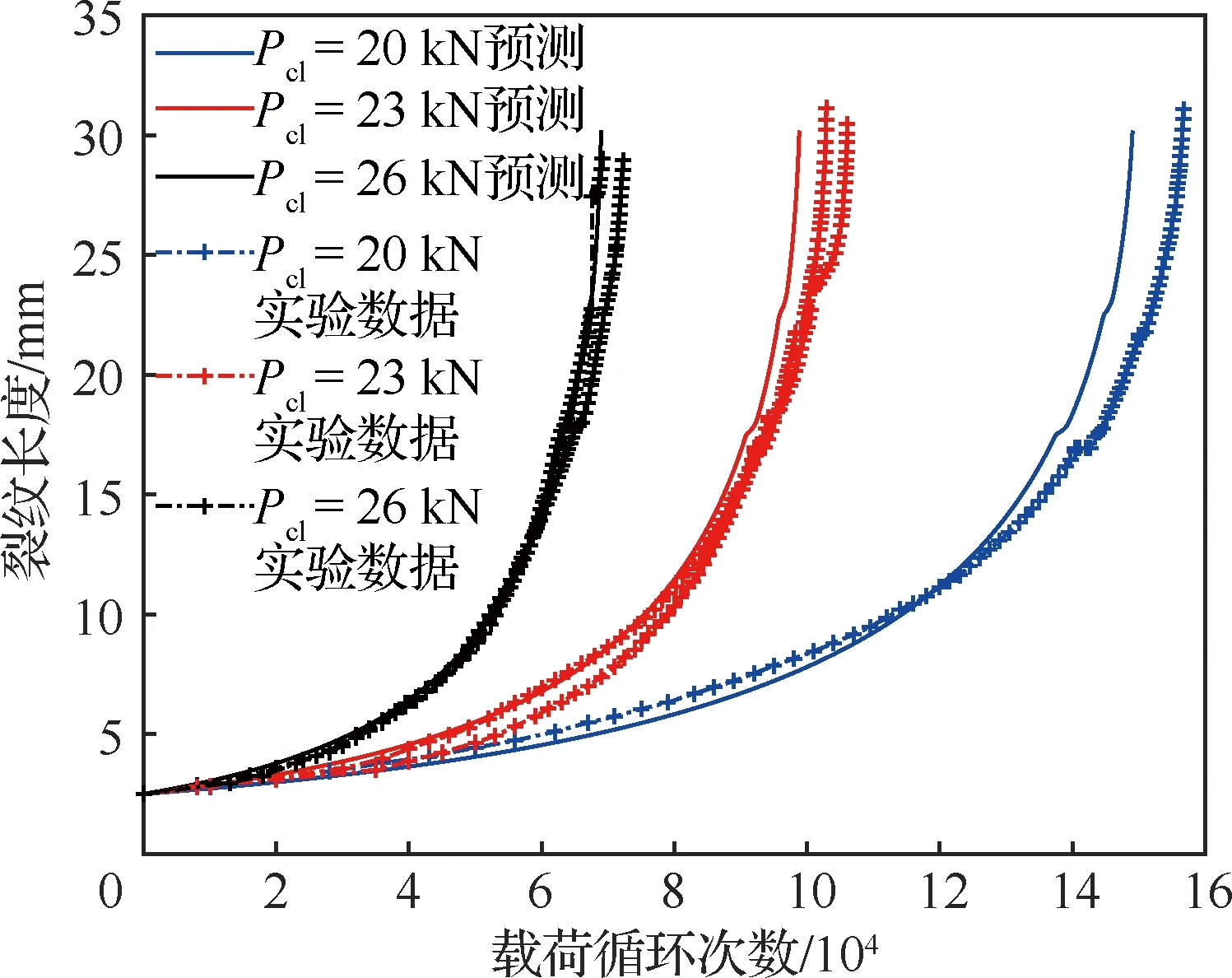
图9 7075-T6铝合金试样裂纹扩展的确定性趋势预测Fig.9 Predicted determinate trends of crack growth of specimens with aluminium alloy 7075-T6

3.1.4 模型对比分析

本文所提出的模型考虑了小时间尺度下疲劳裂纹扩展过程中时间维度的不确定性的动态变化特征以及物理属性、外界载荷和裂纹阈值3个方面的认知不确定性的静态特征，记为模型，本节对该模型在疲劳裂纹扩展的确定性趋势描述和不确定性量化中的表现展开讨论和分析。为此，需要选择不同的对比模型。

文献[19]中考虑了疲劳裂纹扩展实验中物理属性、外界载荷和裂纹阈值的认知不确定性，并采用不确定分布量化描述(记为模型)。其模型形式为在式(8)～式(10)的基础上，假设其、和分别服从正态不确定分布，具体模型可参考文献[19]。模型与本文所提出模型都是在不确定理论框架下量化不确定性，主要区别在于未考虑时间维度的不确定性的动态变化特征。该文献中为了对比概率论和不确定理论在不确定性量化方面的表现，用于与对比的模型考虑物理属性、外界载荷和裂纹阈值具有随机不确定性，并采用概率分布量化(记为模型)。其模型形式为在式(8) ～式(10)的基础上，假设其中的、和分别服从正态分布。相比本文所提出的模型，模型未考虑时间维度的不确定性的动态变化特征，并且在概率论框架下量化不确定性。

本文选用模型和作为对比模型展开讨论分析，且模型中不确定分布的参数估计以及模型中概率分布的参数估计均基于最小二乘原理，详细参数估计方法可参考文献[19]。

1) 确定性趋势预测对比

根据图4、表1和表2的实验数据，进行统计分析分别得到模型和的未知参数估计值。与3.1.3节方法一样，利用、和的数学期望，结合式(8)～式(10)得到裂纹扩展的确定性趋势，并与实验数据进行对比，结果如图10所示。从图中可以发现，模型对于裂纹扩展确定性趋势的预测相比和更为准确，并且模型和的预测结果基本重合。进一步地，本文提出预测结果与实验数据的均方根误差RMSE作为确定性趋势预测准确性的衡量指标，其计算公式为

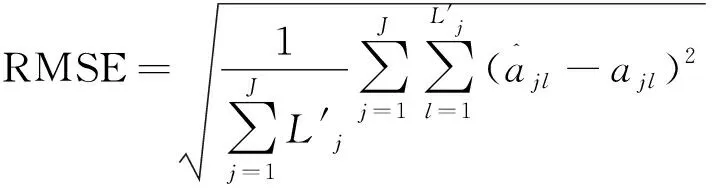
(27)

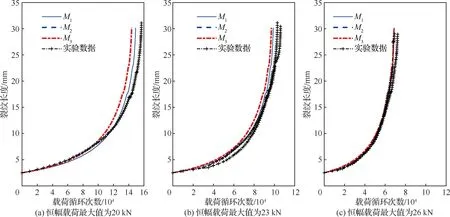
图10 模型M1、M2和M3对于7075-T6铝合金试样疲劳裂纹扩展确定性趋势预测的对比Fig.10 Comparison of models M1, M2 and M3 in predicting determinate trends of fatigue crack growth of specimens with aluminium alloy 7075-T6

2) 不确定性量化结果对比

对不确定性是否细致分类和科学量化，会影响裂纹扩展过程的预测，为此本文利用模型、和在预测裂纹扩展过程时的90%置信区间进行对比分析。

通过仿真得到500组裂纹扩展曲线，并将这500组裂纹扩展曲线上裂纹长度的第5和95百分位数分别作为下边界和上边界，从而得到模型、和预测裂纹扩展过程时的90%置信区间。通过上述方法计算不同模型在预测裂纹扩展过程时的90%置信区间，并与实验数据进行对比，结果如图11所示。从图中可以看出，模型的90%置信区间的范围相比模型和更小，体现了本文所提出的模型在不确定性量化结果中的优势。

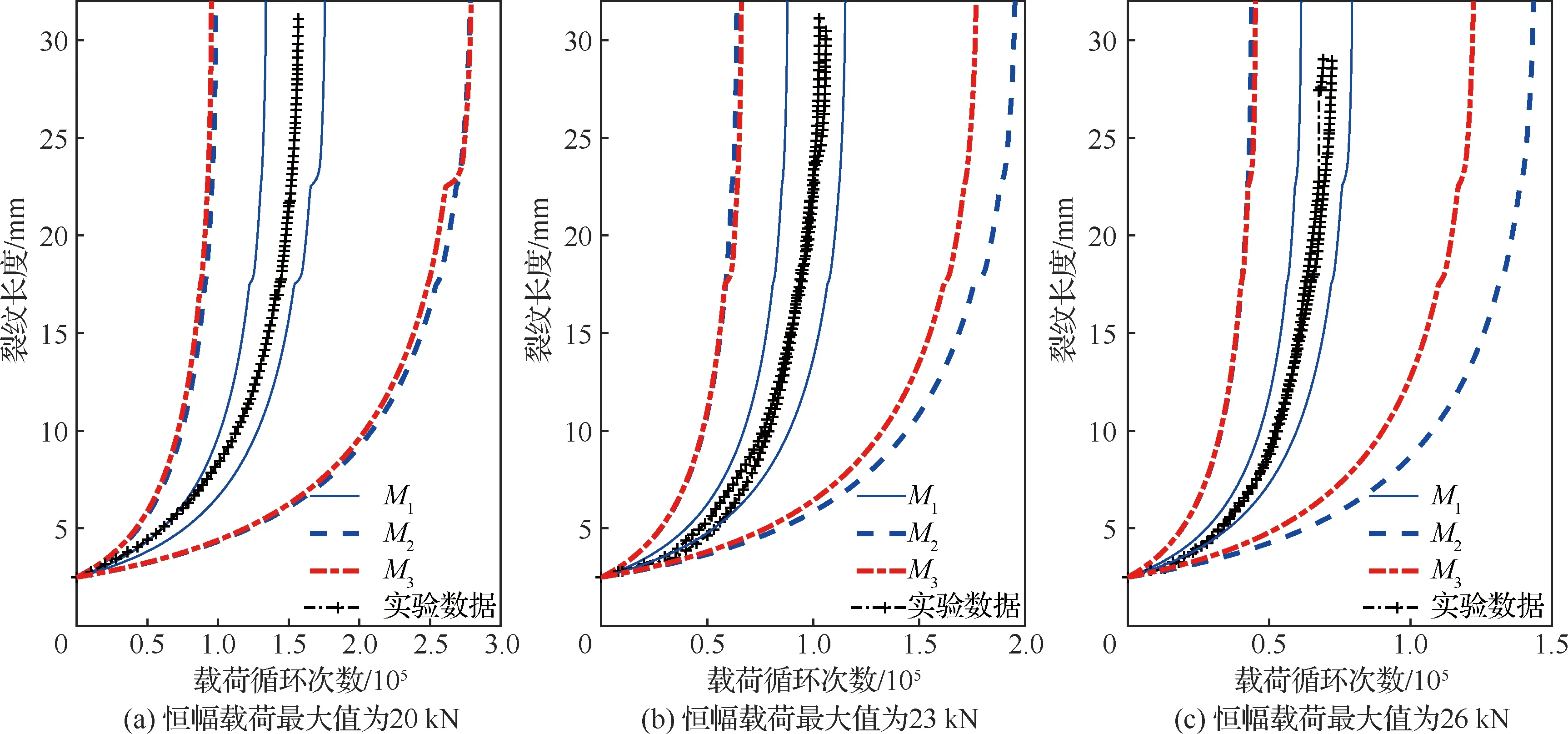
图11 模型M1、M2和M3对于7075-T6铝合金试样疲劳裂纹扩展中不确定性量化的对比Fig.11 Comparison of models M1, M2 and M3 in quantifying the uncertainty of fatigue crack growth of specimens with aluminium alloy 7075-T6

通过上述模型对比分析发现，本文所提出模型在裂纹扩展确定性趋势预测和不确定性量化结果中均体现出优势。一方面是因为本文所提出的模型从小时间尺度出发，基于不确定微分方程进行疲劳裂纹扩展建模，能够更加细致刻画裂纹扩展过程和充分利用实验数据信息，从而在确定性趋势预测中更加准确；另一方面是因为本文所提出的模型相比模型和考虑了疲劳裂纹扩展过程在时间维度的不确定性的动态变化特征，更加全面地考虑了不确定性的来源，同时基于不确定理论量化描述了不确定性的动态变化特征，从而在不确定性量化方面所得到的区间范围更接近实际数据。这表明从小时间尺度出发进行疲劳裂纹扩展建模以及对不确定性进行细致分类和科学量化的重要意义。

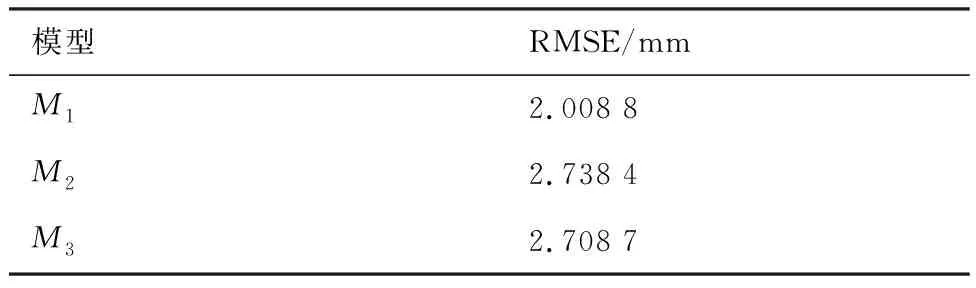
表4 模型M1、M2和M3对于确定性趋势预测的RMSE计算结果

3.1.5 参数不确定性的敏感性分析

在工程应用中，可以通过控制或干预不确定性来减小风险，那么就需要辨识各种不确定性的影响，即物理属性、外界载荷和裂纹阈值3个方面的不确定性的静态特征以及时间维度的不确定性的动态特征对裂纹扩展过程预测的影响。

物理属性、外界载荷和时间维度的不确定性会影响整个裂纹扩展过程，而裂纹阈值的不确定性仅影响裂纹扩展过程的终止条件。因此进行物理属性、外界载荷和时间维度3个方面的参数不确定性的敏感性分析时，采用3.1.4节中的方法比较裂纹长度的90%置信区间。而对于裂纹阈值的参数不确定性的敏感性分析，因为裂纹阈值对于裕量的影响伴随着整个裂纹扩展过程，因此采用裂纹裕量的90%置信区间来表征裂纹阈值的不确定性的影响。

时间维度、物理属性、外界载荷和裂纹阈值4个方面的不确定性分别以动态噪声项·dd、材料参数、过载比和临界裂纹长度的标准差来表征，为了比较这4个方面的不确定性对于裂纹扩展过程预测的影响，作以下分析和计算：

1) 在时间维度方面。式(11)中扩散系数表示了动态噪声项的标准差，进而反映时间维度的不确定性大小，因此设置扩散系数分别为0.5、0.8、1.2和1.5，其中的取值为3.420 9×10，4组扩散系数设置下其余模型参数均如表3所示。4组不同的扩散系数设置下通过仿真分别得到500组裂纹扩展曲线，从而计算裂纹长度的90%置信区间，结果如图12(a)所示。

2) 在物理属性方面。设置材料参数的标准差分别为0.5、0.8、1.2和1.5，其中的取值为7.605 9×10，4组材料参数标准差设置下其余模型参数与表3一致，然后通过仿真方法计算裂纹长度的90%置信区间，结果如图12(b)所示。在外界载荷方面，过载比标准差的设置方法以及裂纹长度的90%置信区间计算方法与物理属性方面类似，不再赘述，结果如图12(c)所示。

3) 在裂纹阈值方面。设置临界裂纹长度的标准差分别为0.5、0.8、1.2和1.5，其中的取值为1.58，4组临界裂纹长度标准差设置下其余模型参数与表3一致。通过500次仿真得到500组裂纹扩展曲线和500组裂纹阈值，然后分别以裂纹阈值减去裂纹长度得到裂纹裕量的变化曲线，从而计算裂纹裕量的90%置信区间，结果如图12(d)所示。

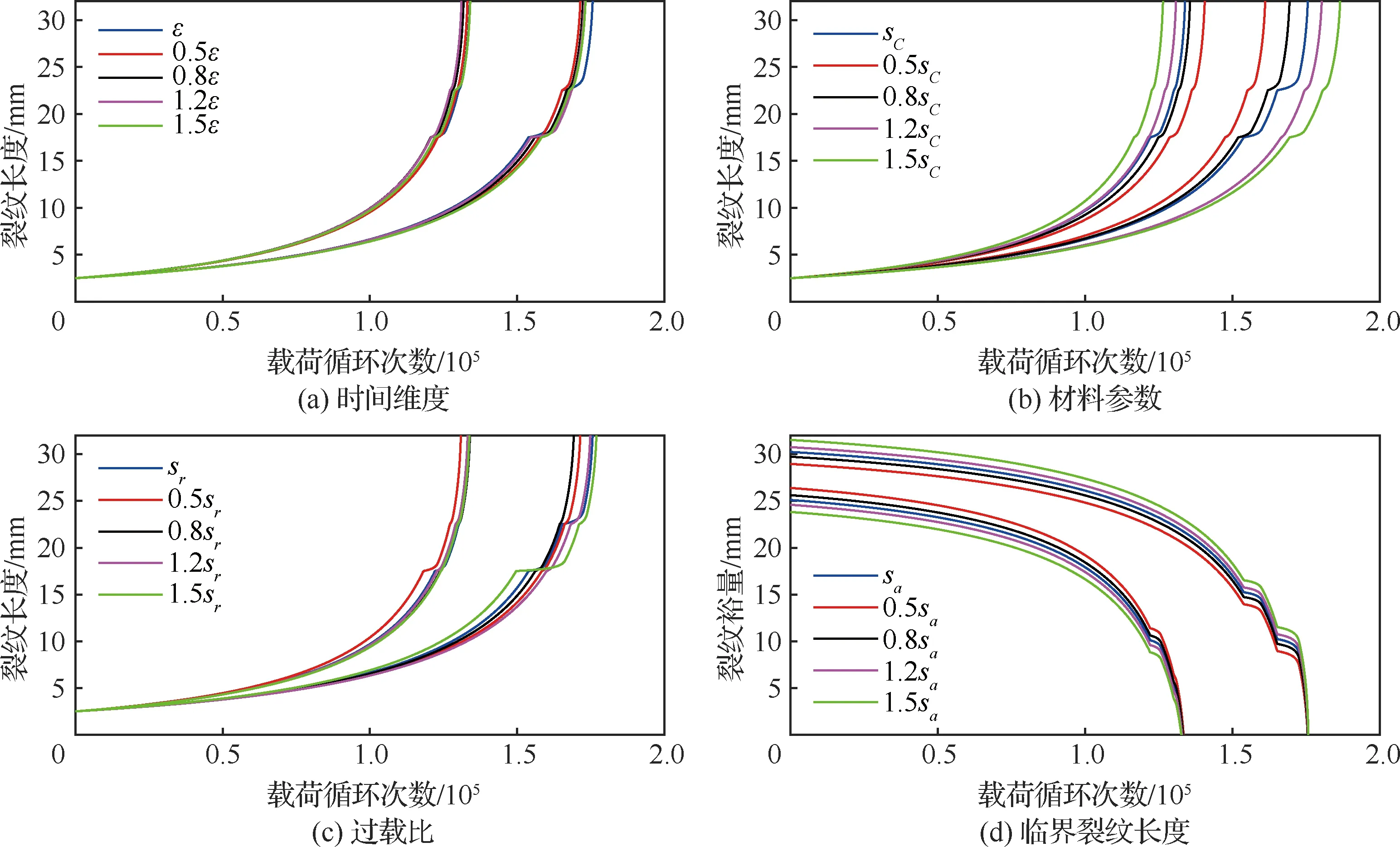
图12 恒幅载荷最大值为20 kN时不同标准差设置下裂纹长度或裂纹裕量的90%置信区间Fig.12 90% confidence intervals of crack length or crack margin under different standard deviations when the maximum of constant amplitude loadings is 20 kN

图12展示了恒幅载荷最大值为20 kN时时间维度、物理属性、外界载荷和裂纹阈值4个方面不同标准差大小设置下裂纹长度或者裂纹裕量的90%置信区间，反映了各方面的不确定性大小对于裂纹扩展过程预测的影响。从图中可以看出，材料参数的标准差大小对于裂纹长度的90%置信区间影响较为明显，即标准差设置越大，裂纹长度的90%置信区间越宽；在不同的时间维度扩散系数和过载比的标准差设置下计算得到的裂纹长度的90%置信区间比较接近，表明时间维度和过载比的不确定性大小对于裂纹扩展过程预测的影响较弱；而临界裂纹长度的标准差大小会对裂纹裕量的90%置信区间产生显著影响。

进一步，提出平均相对误差MRE这一量化指标来对比不同参数的不确定性大小对于裂纹扩展过程预测的影响，即

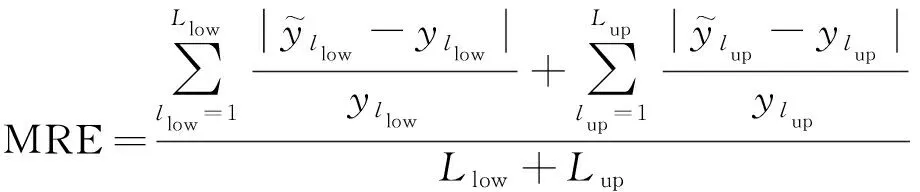
×100%

(28)

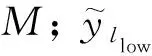
根据式(28)计算恒幅载荷最大值为20 kN时时间维度、物理属性、外界载荷和裂纹阈值4个方面在0.5倍、0.8倍、1.2倍和1.5倍标准差设置下相比1倍标准差下所预测的90%置信区间的MRE，计算结果如图13所示。从图中可以发现，材料参数和临界裂纹长度的标准差在不同设置下得到的MRE值相比时间维度和过载比较大，表明材料参数的不确定性对于裂纹长度预测的影响较大，同样临界裂纹长度的不确定性对于裂纹裕量预测的影响较大。采用同样的方法分别计算恒幅载荷最大值为23 kN和26 kN时不同标准差设置下的MRE值，计算结果如图14和图15所示。图14结果表明材料参数和临界裂纹长度的不确定性对裂纹扩展过程预测的影响较大，而图15中在0.8倍和1.5倍标准差设置下，过载比对应的MRE值均最大，分析原因是恒幅载荷最大值为26 kN时，过载比标准差的变化会造成高载幅值范围更大程度的变化，而高载幅值会影响裂纹尖端的力学特性，进而对裂纹扩展过程预测产生较大影响。

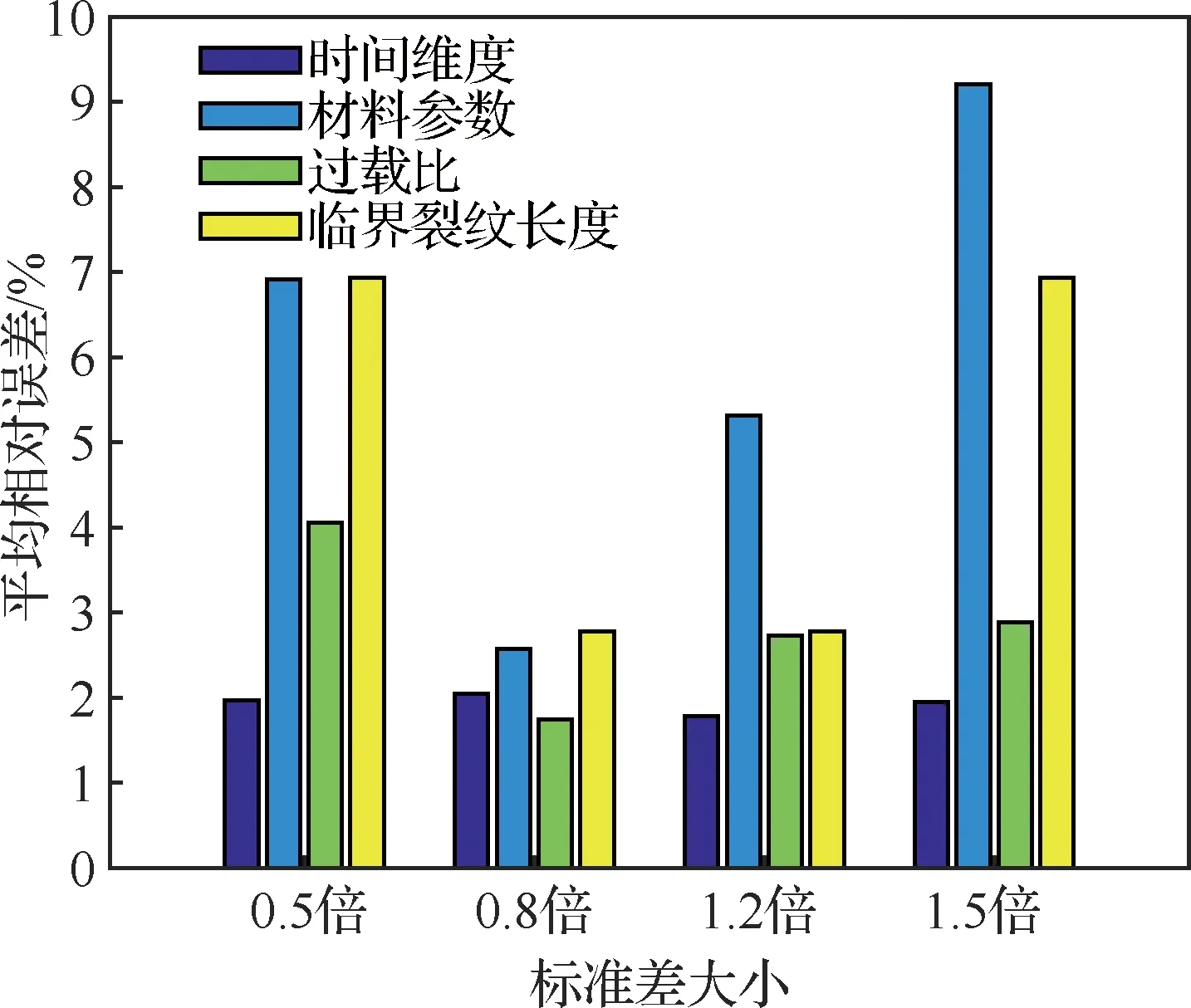
图13 恒幅载荷最大值为20 kN时不同标准差设置下的MRE计算结果Fig.13 Calculation results of MRE under different standard deviations when the maximum of constant amplitude loadings is 20 kN

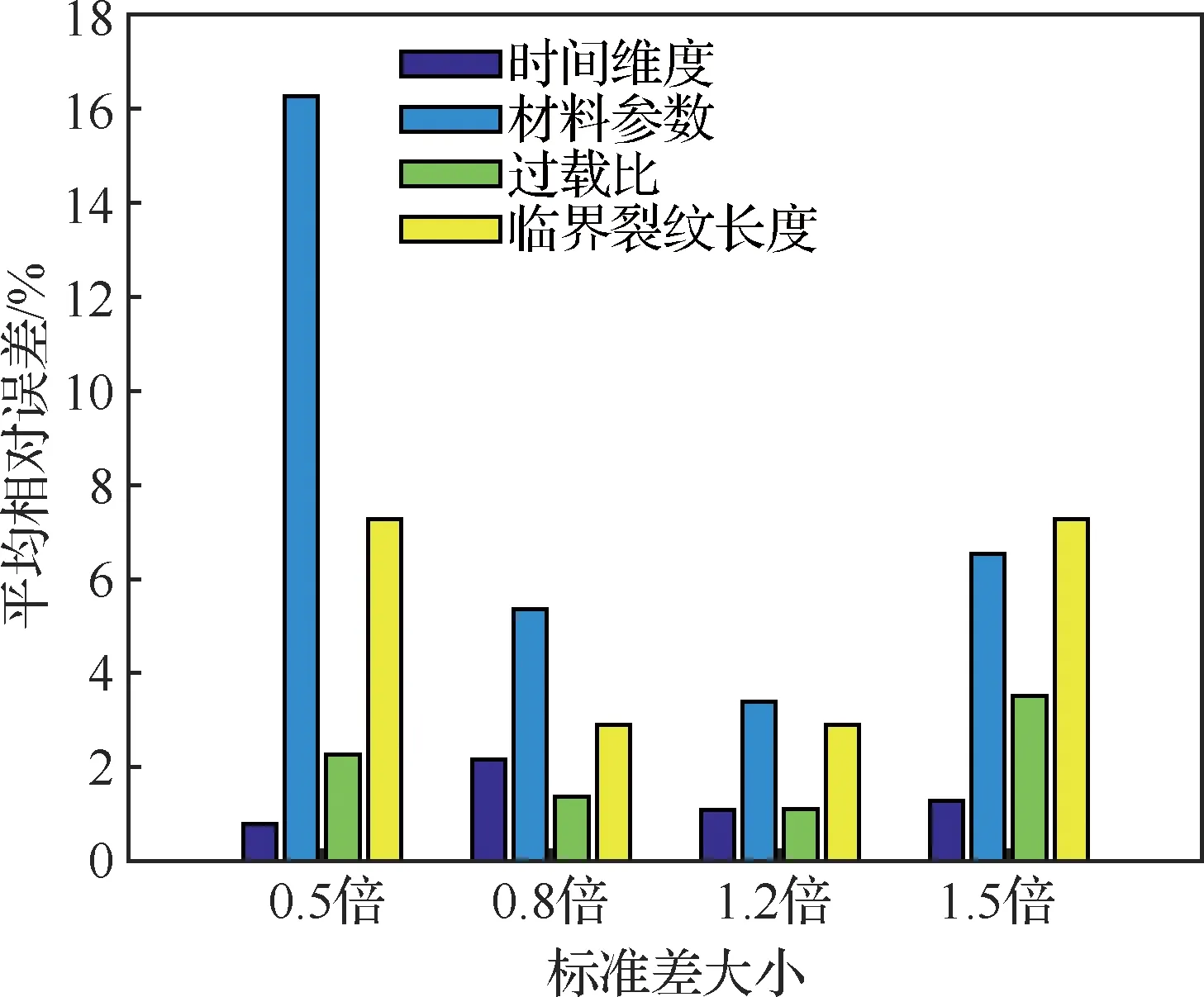
图14 恒幅载荷最大值为23 kN时不同标准差设置下的MRE计算结果Fig.14 Calculation results of MRE under different standard deviations when the maximum of constant amplitude loadings is 23 kN

图15 恒幅载荷最大值为26 kN时不同标准差设置下的MRE计算结果Fig.15 Calculation results of MRE under different standard deviations when the maximum of constant amplitude loadings is 26 kN

进一步，计算不同恒幅载荷最大值下MRE结果的平均值，结果如表5所示。表5中不同标准差设置下材料参数和临界裂纹长度对应的MRE值相比时间维度和过载比均较大，这与图13～图15所分析的结果相对应，表明了材料参数和临界裂纹长度的不确定性对于裂纹扩展过程预测的影响需要重点考虑。

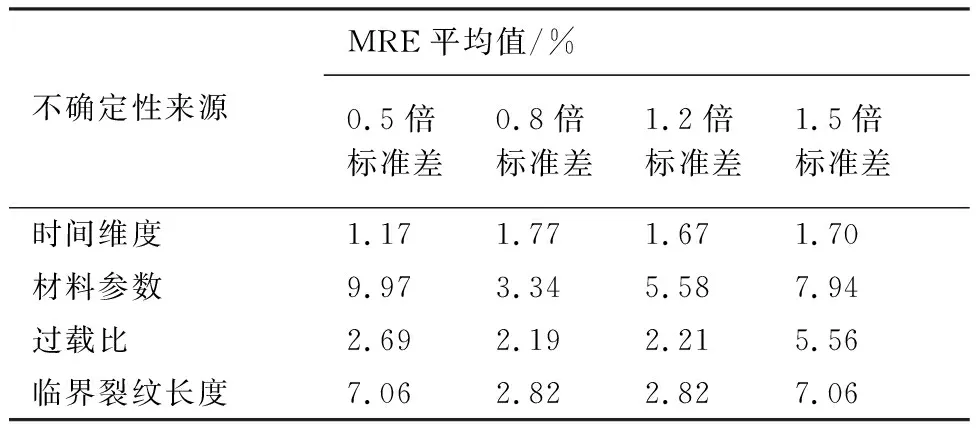
表5 不同恒幅载荷最大值下MRE的平均值

工程生产中，控制或干预材料参数的不确定性可以通过筛选材料、鉴定力学特性和保证产品加工质量(如表面光洁度)等措施来完成。临界裂纹长度的不确定性是很难控制或干预的，因此可以设计裂纹长度的安全阈值，当裂纹长度接近安全阈值时采取维修或更换措施，从而降低产品生产和使用风险，例如将95%置信水平下临界裂纹长度的单侧置信限作为安全阈值，即通过求解式(29)所示方程，结果为27.61mm。

M{≤}=1-()=095

(29)

3.2 基于Virkler疲劳数据集的分析

3.2.1 实验设置及实验数据

本节基于Virkler疲劳数据集分析并验证本文提出模型的有效性。Virkler等的疲劳裂纹扩展实验中用2024-T3铝合金制备了预制裂纹长度为9 mm的中心裂纹拉伸试样，在相同的恒幅载荷条件和环境条件下进行了68次重复实验，每次实验记录了9～49.8 mm范围内共计164组裂纹长度对应的载荷循环次数。试样几何尺寸和实验条件的详细信息可参考文献[1]。该实验得到的疲劳数据如图16所示。

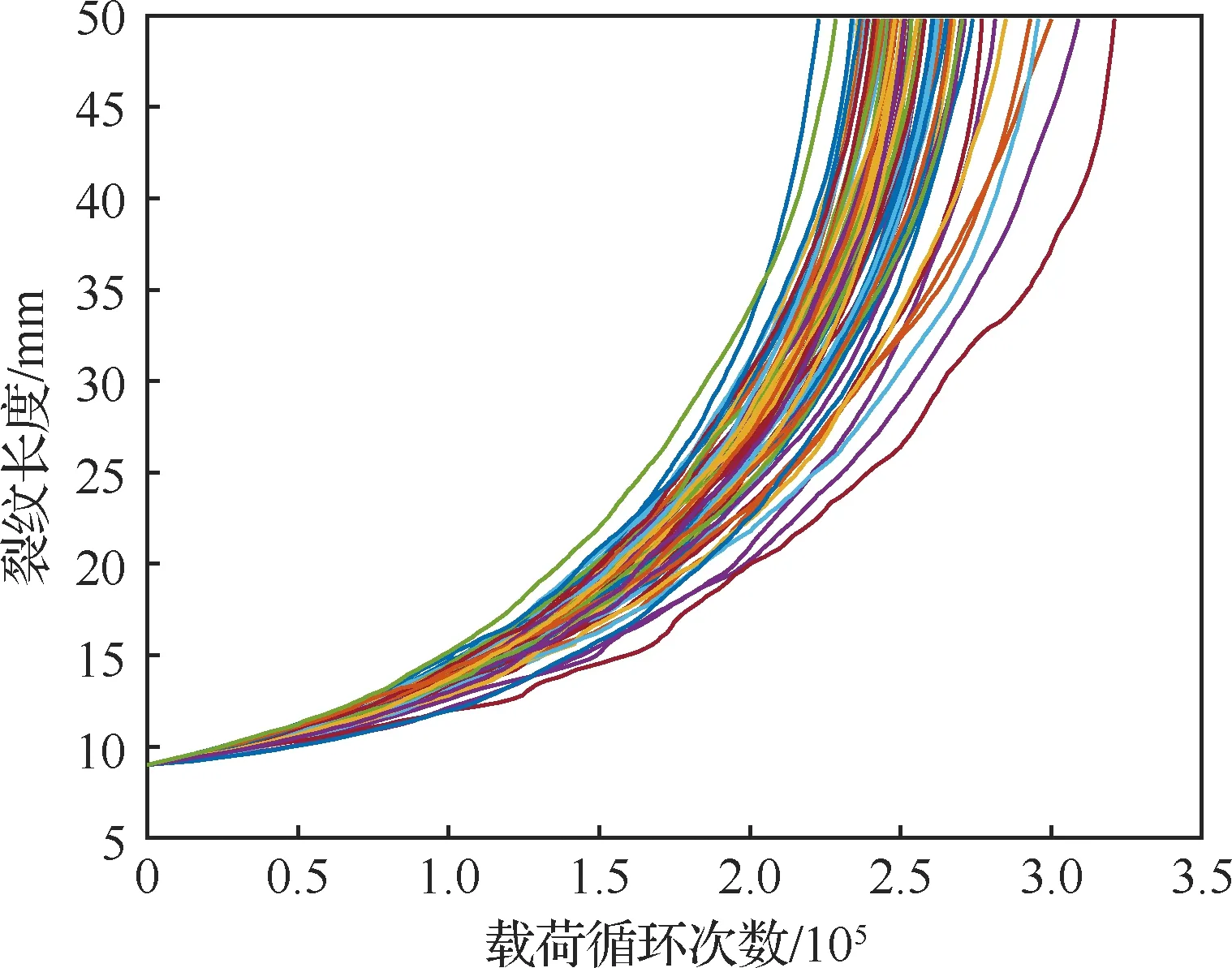
图16 Virkler等的疲劳裂纹扩展实验数据[1]Fig.16 Data of FCGE of Virkler et al.[1]

3.2.2 参数估计结果及确信可靠度评估结果

对照本文所提出的模型，Virkler疲劳数据集中体现出物理属性的不确定性的静态特征和时间维度不确定性的动态特征，实验中不施加高载，临界裂纹长度取常值49.8 mm，这种情况下本文所提出模型依然适用。因此，根据图16中裂纹长度和载荷循环次数，通过2.2节统计分析方法，得到未知参数的估计结果如表6所示。实验数据不含高载信息，所以与高载幅值相关的未知参数{,}缺省。另外，对于固定的临界裂纹长度，其标准差取0。

表6 基于Virkler等的疲劳数据集的未知参数估计结果

根据表6参数估计结果和确信可靠度函数式(14)，计算确信可靠度在恒幅载荷最大值为23.35 kN下(即实验载荷条件)随载荷循环次数的变化关系，得到确信可靠度评估结果如图17所示。

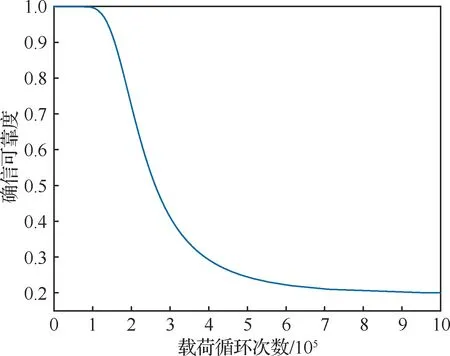
图17 2024-T3铝合金试样的确信可靠度评估结果Fig.17 Result of belief reliability evaluation of specimens with aluminium alloy 2024-T3

3.2.3 模型验证分析

本节将进一步从疲劳裂纹扩展的确定性规律描述和不确定性量化方面展开分析，基于、和开展对比分析，验证本文模型的有效性。

3.1.4节以模型预测的疲劳裂纹扩展过程的均值和90%置信区间分别表征确定性趋势和不确定性量化结果，对模型、和进行了对比分析。本节基于Virkler疲劳数据集，采用与3.1.4节相同的方法分别计算模型、和预测的疲劳裂纹扩展过程的均值和90%置信区间，详细计算方法和过程不再赘述，计算结果分别如图18和图19所示。

图18展示了实际数据的均值，以及模型、和对于裂纹扩展过程确定性趋势的描述结果，可以发现模型、和预测的均值都未完全符合实际数据均值，并且模型和预测的均值基本接近。直观上不容易对比模型、和预测裂纹扩展过程的确定性趋势的准确性，因此以给定裂纹长度下不同模型预测均值曲线上对应的载荷循环次数相比实际数据对应的载荷循环次数均值的平均相对误差来表征模型的准确性。模型、和对应的平均相对误差计算结果分别为4.50%、6.54%和6.66%，表明本文模型在裂纹扩展确定性趋势预测中相比和更加准确。图19展示了全部实际数据，以及模型、和预测裂纹扩展过程时的90%置信区间，可以直观地发现，模型预测的区间范围相比模型和更窄，而且模型预测的区间范围更接近实际数据的边界，体现出本文模型在不确定性量化结果中的优势。

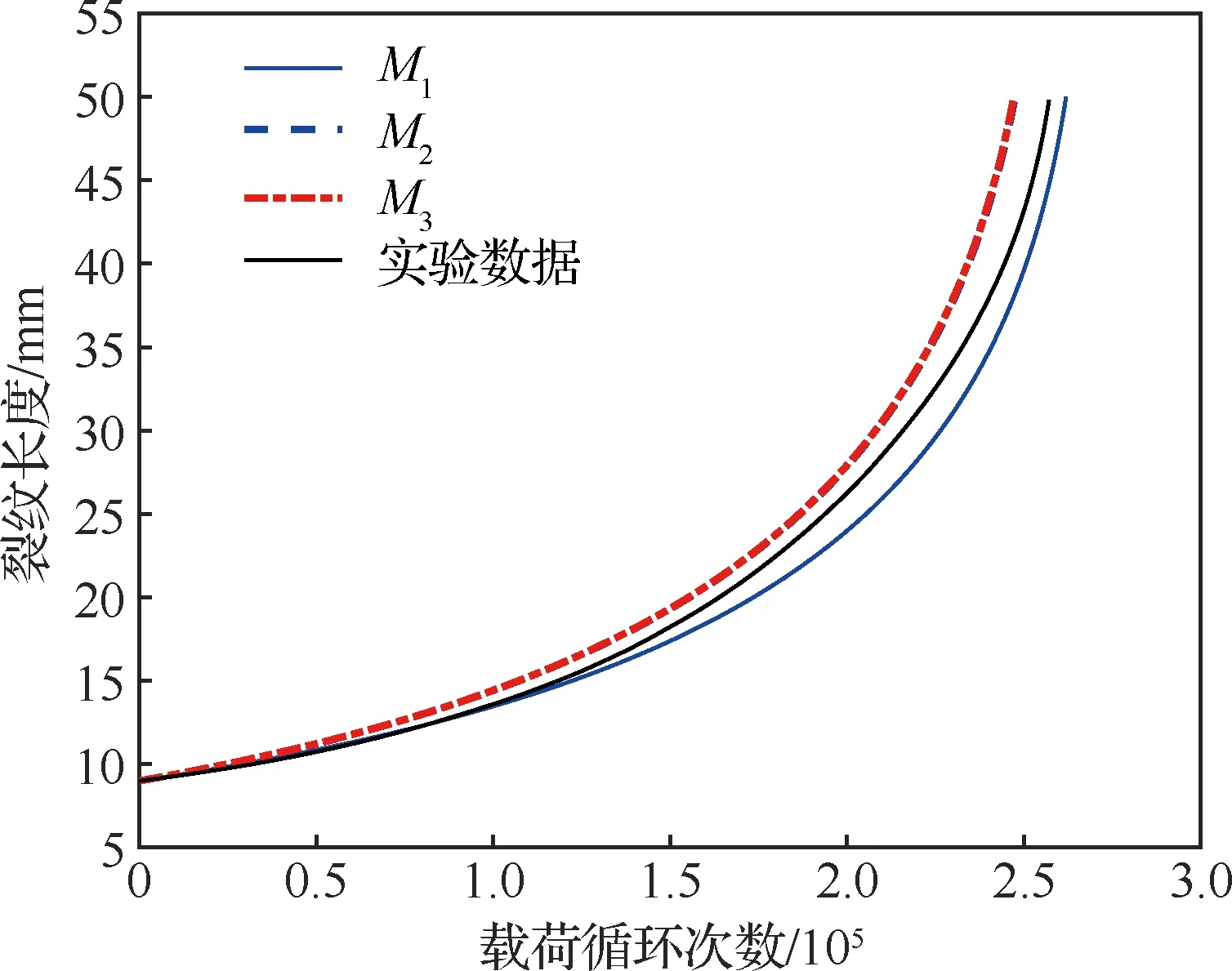
图18 模型M1、M2和M3对于2024-T3铝合金试样疲劳裂纹扩展的确定性趋势预测的对比Fig.18 Comparison of models M1, M2 and M3 in predicting the determinate trends of fatigue crack growth of specimens with aluminium alloy 2024-T3

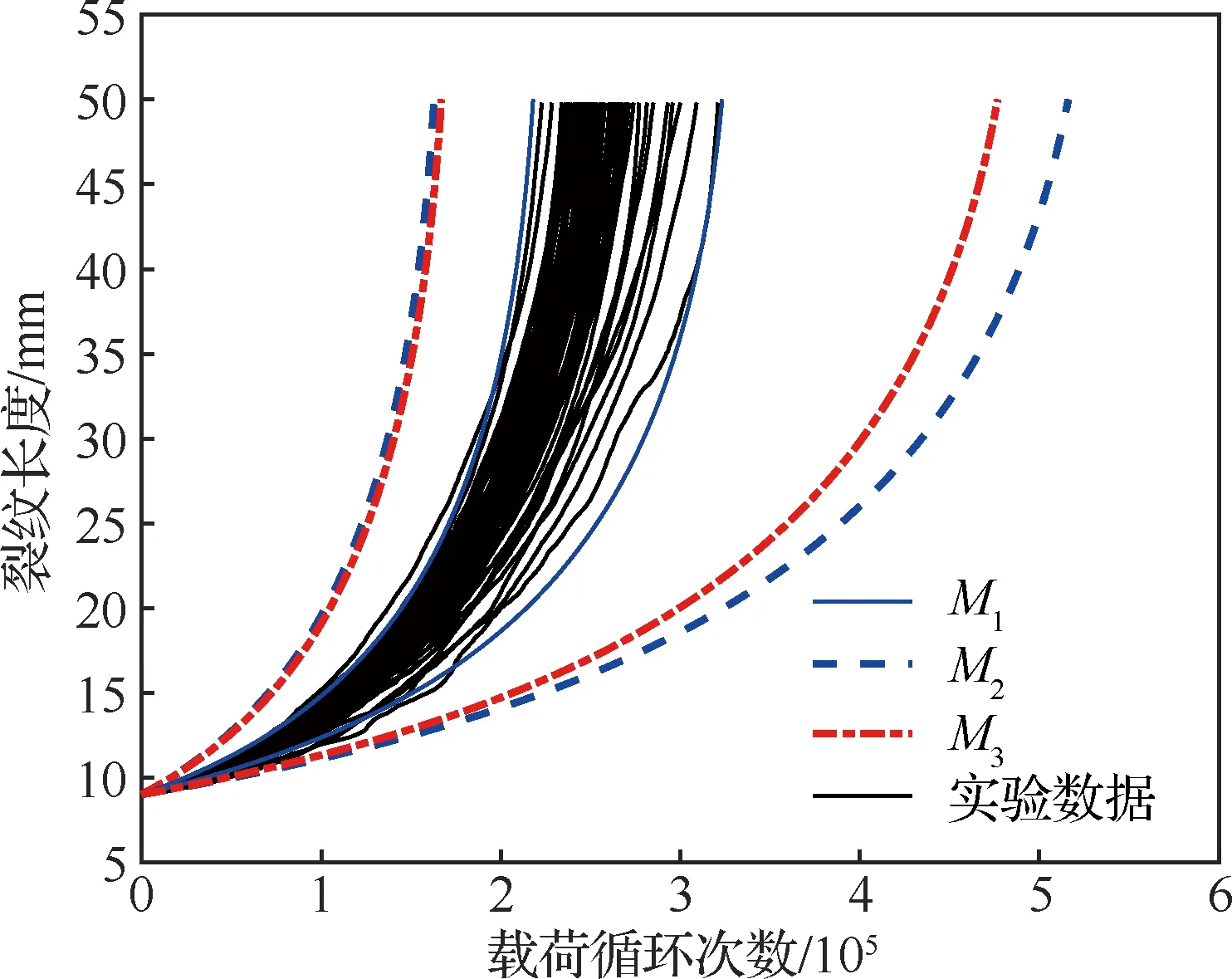
图19 模型M1、M2和M3对于2024-T3铝合金试样疲劳裂纹扩展中不确定性量化的对比Fig.19 Comparison of models M1, M2 and M3 in quantifying uncertainty of fatigue crack growth of specimens with aluminium alloy 2024-T3

通过Virkler疲劳数据集的分析，本文所提出的模型相比模型和在疲劳裂纹扩展的确定性趋势预测和不确定性量化方面都具有优势，与3.1.4节得到的结论相一致，验证了本文所提出模型的有效性。关于模型、和的区别以及模型区别对于确定性趋势预测和不确定性量化结果的影响在3.1.4节已经详细说明，这里不再赘述。