基于互相关移位相乘BOC(m,n)无模糊捕获算法

2022-09-09李明胡辉郭萌禹飞谢虹群

航空学报 2022年8期

李明，胡辉，郭萌，禹飞，谢虹群

华东交通大学信息工程学院，南昌 330013

全球卫星导航系统(Global Navigation Satellite System，GNSS)在各行各业的应用越来越广泛，目前卫星导航正由单GPS(Global Positioning System)进入多星座联合的GNSS时代，传统的卫星导航信号的调制方式使得各种导航信号在有限频段内重叠，相互干扰。二进制偏移载波(Binary Offset Carrier，BOC)调制是以方波作为子载波对伪随机(Pseudo Random Noise，PRN)码进行预调制，使得信号频谱对称分裂于频带边缘，并且可以通过选择不同的调制参数来调整两个分裂主瓣的间距，从而有效解决导航信号间的相互干扰，实现频谱资源的有效利用。

虽然BOC调制有效解决了上述问题，但在±1码片内，BOC信号自相关函数(AutoCorrelation Function,ACF)存在多峰性，使得BOC信号捕获存在两方面的问题：一是误捕到旁峰造成捕获模糊，影响了测距精度；二是相关峰存在的多个零点导致信号漏捕。

近年来，针对上述存在的问题，已经提出了多种方法，目前国内外主要成果有：多载波模型BPSK-Like法，将BOC信号视为无穷个叠加的BPSK(Binary Phase Shift Keying)信号之和，通过本地产生对应的载波来剥离主载波和子载波，最终生成一个类似BPSK信号的单相关峰。这虽然解决了误捕旁峰的问题，但其主峰宽度与BPSK相同，为2个码片，不能保证BOC信号窄相关峰特性。自相关旁锋消除法(Autocorrelation Side-peak Cancellation Technique, ASPeCT)利用了BOC(,)信号自相关函数和BOC(,)/PRN的互相关函数在相同码相位处，旁峰具有类似的特点，通过调整权值系数，减小旁峰与主峰的峰值比，但最优效果难以保证。另外，该算法仅适用于=的情况。子载波相位消除法(Subcarrier Phase Cancellation, SCPC)借鉴了主载波剥离的思想，首先本地产生两路子载波相位正交的BOC信号，然后将BOC、QBOC(Quadrature BOC)的互相关函数平方与BOC的自相关函数平方相加，最终得到了检测峰不含零点的相关曲线，该方法解决了漏捕问题，但BOC信号窄相关峰特性得不到保证。综上所述，目前的主流算法或者能消除多峰性而不能保留BOC信号窄相关峰特性，或者能够保留BOC信号窄相关峰特性，但多峰性明显，甚至有些仅适用于BOC(,)类信号。

目前，相关函数重构算法是一个比较热门的方向，它的核心思路是将相关函数分离成一系列子相关函数，利用子相关函数之间的特点，通过翻转、非线性、截取移位、线性等方法，重新构造一个无旁峰干扰的新相关函数，进而解决BOC信号存在的误捕和漏捕问题。文献[18]提出的CSSPeCT(Correlation Shift-SidePeak Cancellation Technique)技术，将相关函数分离为奇偶两部分，降低了分离和重构过程的复杂度，但其仅适用于=的情况。文献[19]利用自相关函数与自相关绝对值函数主峰大小相等、方向相同、旁峰大小相等、方向相反的特点，给出了一种合成互补方法：该方法对自相关函数的调幅、截取等操作，受接收信号的码相位偏移及多普勒频移影响，而接收信号的相关信息是随机的。文献[20]提出了一种运算量更低且适用于任意阶数BOC信号的捕获算法，其结果存在一定的负峰，牺牲了一定的性能。

针对现有技术存在的问题，本文提出了一种基于互相关函数分离重构的无模糊捕获算法。同时，为了解决该算法运算量大以及适用性单一的问题，提出了一种快速算法。

1 算法分析

1.1 BOC调制信号模型

通常，BOC调制信号以BOC(,)来表示，其中表示信号的子载波频率与基准频率之比，为PRN码码速率与的比值，=1.023 MHz，记=2为BOC调制阶数，其信号特性主要受子载波频率和PRN码码速率的比值影响，即与调制阶数密切相关。

由于BOC信号中的PRN码序列和子载波具有特定的相关性，BOC(,)信号的自相关函数ACF除主峰之外还存在多个旁峰。BOC(1,1)信号的自相关函数的模型为

(1,1)()=

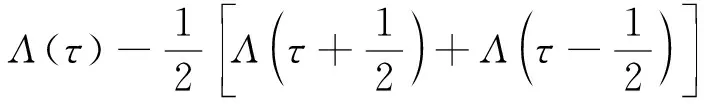
(1)

式中：()为高度1、宽度2、中心在=0处的三角函数；为码相位延迟。BOC/PRN互相关函数即为BOC信号与不经子载波调制的PRN进行相关运算得到。BOC(2,1)信号与PRN的互相函数为

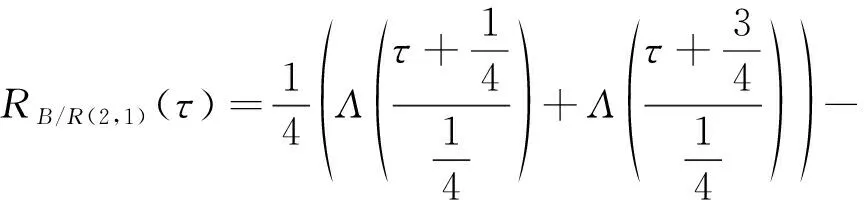
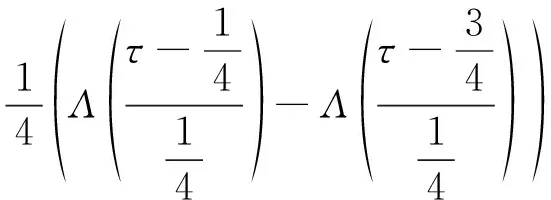
(2)

图1(a)为BPSK、BOC(1,1)和BOC(2,1)自相关函数MATLAB仿真的结果比较，图1(b)为BOC(1,1)/BOC(2,1)与PRN码的互相关函数对比。由图可知，BPSK信号自相关函数只有一个峰值，而BOC(1,1)信号自相关函数主峰宽度只有BPSK的一半，BOC(2,1)则为1/4，这使得BOC信号具有更好的跟踪精度，但其自相关函数有多个旁峰，这就导致捕获过程中存在误捕的情况。调制阶数越高，BOC信号主峰宽度越窄，同时其旁峰数量也越多，旁峰幅值大小越接近主峰，如何将旁峰去除就成了解决问题的关键。

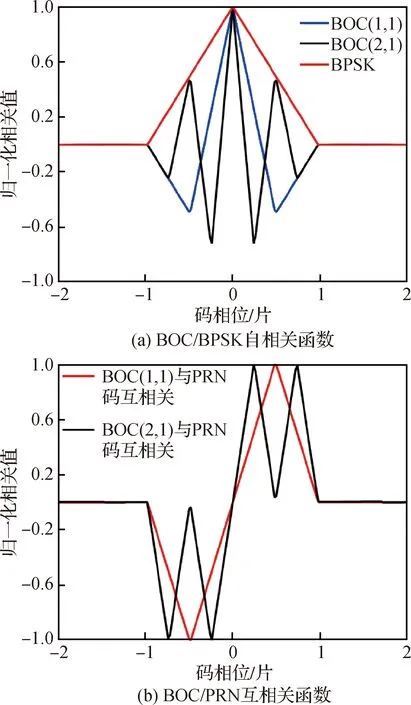
图1 BOC信号相关函数比较Fig.1 Comparison of BOC signal correlation functions

BOC信号与PRN码的互相关函数分为左右两部分，这两部分关于中心原点对称，每一部分都是由多个三角峰组成，其峰值大小的绝对值相等。与自相关函数相同，互相关函数随着调制阶数的增加，每个部分中的相关峰个数增多，宽度变窄，其总个数随调制阶数变化的关系为=，即两部分三角峰个数之和等于信号调制阶数。

对于BOC信号来说，若在捕获过程中没有将旁峰消去，而误捕到了旁峰，在后续的跟踪相位阶段将会导致误锁，特别是高阶的BOC信号，其相关函数的主峰和子峰难以区分，更加容易造成误锁现象，这会引起不容忽视的定位偏差。

1.2 分离重构原理

根据图1(b)所示BOC/PRN互相关函数的性质，我们可对互相关函数进行如下分解重组。

本地PRN信号数学模型可表示为

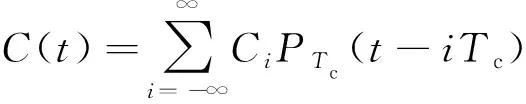
(3)

式中：()为周期为的单位矩形脉冲；为单个PRN码片宽度；∈(-1,1)为第个码片的符号。基于上述信号分离原理，将PRN的每个码片分成等份，截取每一个PRN码片的第一等份，构成第一组子码信号，如式(4)所示：

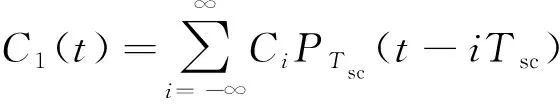
(4)

式中：()为周期为的矩形脉冲；为单个子载波脉冲的宽度，其与PRN码片宽度的关系为=。这样依次截取每个PRN码片的第等份的码片信号，组成第组子码信号()：

()=(-(-1))=1，2，…，

(5)

由式(5)可得第组子码信号()可以由延迟得到，则本地PRN信号被分成组子码信号的和，即为

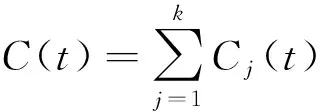
(6)

当输入信号为BOC(2,1)时，调制阶数=4，对应的本地PRN信号的分离结果如图2所示。

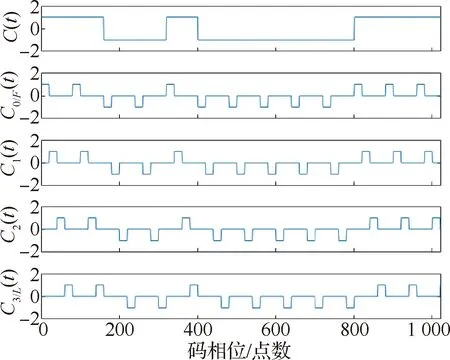
图2 本地PRN信号分离图Fig.2 Decomposition of local PRN

当调制阶数为偶数时，BOC/PRN互相关函数可表示为

()=

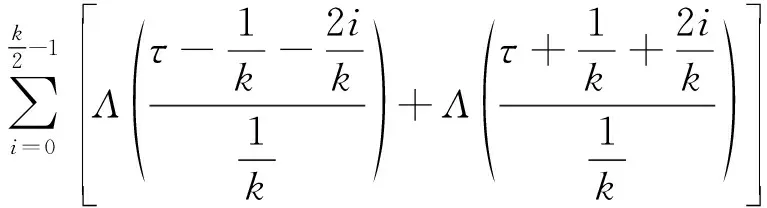
(7)

若定义PRN信号的第组子码信号()与BOC(,)信号的子互相关函数为()，则BOC/PRN互相关函数为个子互相关函数之和：

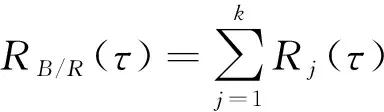
(8)

图3(a)为MATLAB仿真得到的BOC(2,1)信号与PRN信号互相关函数()以及分离后的子互相关函数()结果图，码相位延迟设置为400。

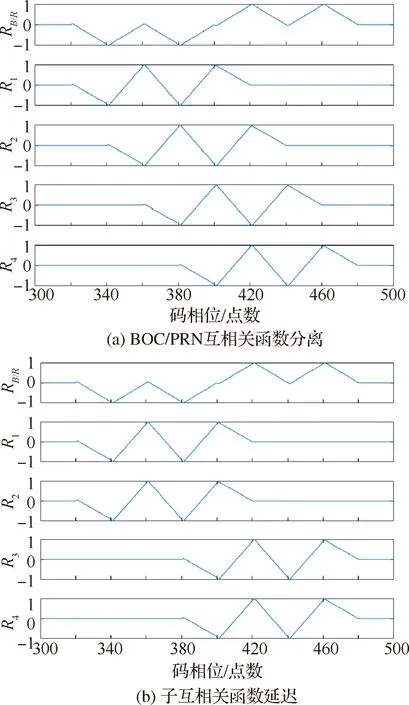
图3 互相关函数分离Fig.3 Decomposition of cross-correlation functions

由图可知子互相关函数()存在峰值相等的多峰，且相邻峰之间的时间延迟均为。若以()为基准，按式(4)中()的定义，则()可由()延迟得到，即

()=(-(-1))=1，2，…，

(9)

若将图3(a)所示的()延迟至与()对齐，将()延迟至与()对齐，结果即为图3(b)所示。此时()和()、()和()关于码相位=400成对称关系，利用该对称性将()和()相乘、()和()相乘可分别得到单峰，再将两个单峰相加得到最终结果。

对于所有为偶数阶的BOC(,)信号都有同样的结论，最终构造得到的相关函数即可用于无模糊度捕获，具体过程如下：

1) 计算分离后的个子相关函数()。

2) 将所有子相关函数分成2组：

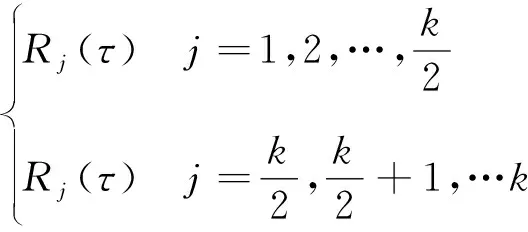
并把第1组中其余子相关函数时延至与()对齐，第2组中与()对齐。

3) 第1组和第2组中互相关于原点对称的子相关函数相乘，即下标之和为的子相关函数两两相乘，得到/2个结果。

4) 所有结果相加得到最终重构的相关函数()，其表达式如式(10)所示，将该算法简记为移位相乘法。

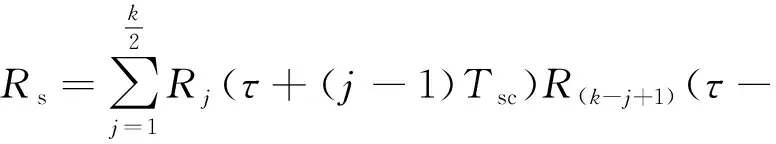
(-1))

(10)

1.3 基于互相关函数分离重构的移位相乘算法

综合1.2节分离重构原理，提出了基于互相关函数分离重构的移位相乘算法，图4显示了该捕获算法的原理框图。图中：NCO为数控振荡器；IFFT表示快速傅里叶逆变换。

输入中频BOC(,)信号的数学模型如下：

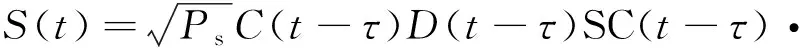
cos(2π(+))+()

(11)

式中：为信号接收功率；()为PRN码序列；()为导航电文；SC()为子载波；为信号中频；为接收信号的多普勒频移；()为噪声部分。

首先，根据式(4)～式(6)将本地信号分离，得到组子码信号；将分离的组子码信号分别和输入中频信号进行互相关运算，这里采用FFT实现。

由于导航电文()在处理过程中幅值恒定，此处忽略其影响，不考虑数据位跳变。假设总共有段数据处理，则第段的数据经积分处理并求模后的输出为

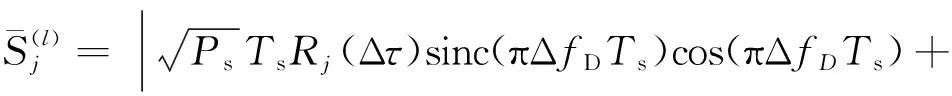
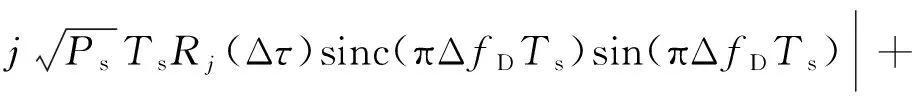
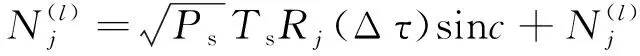
=1,2,…,

(12)

简记为

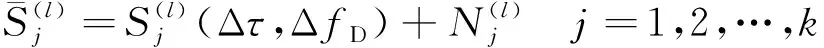
(13)

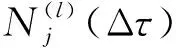
图4 移位相乘算法原理图Fig.4 Schematic diagram of cross-correlation-shift multiplication algorithm

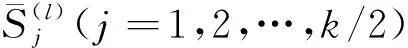
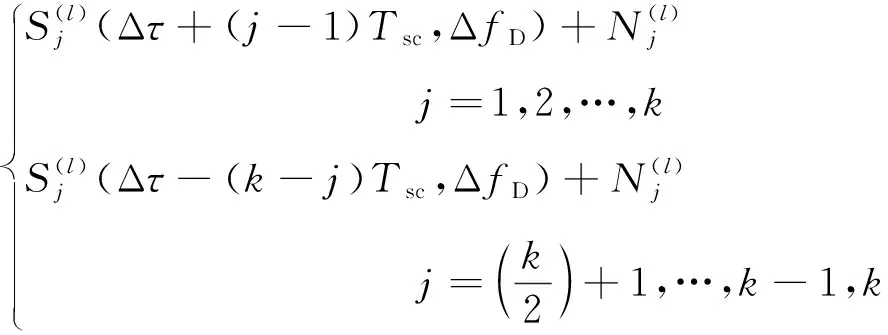
(14)

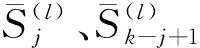
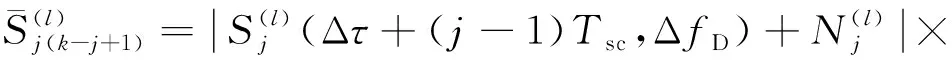
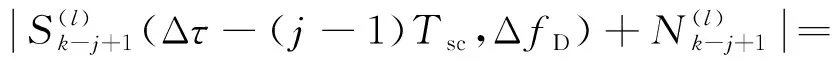
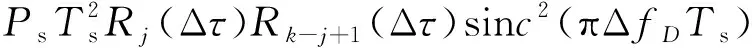
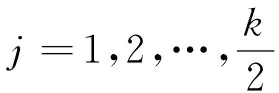
(15)

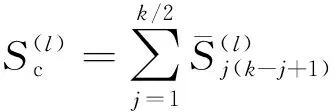
(16)

对于所有的段数据进行非相干累加，即得到图4所示的最终检测量：

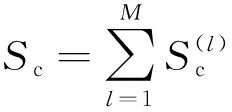
(17)

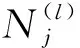
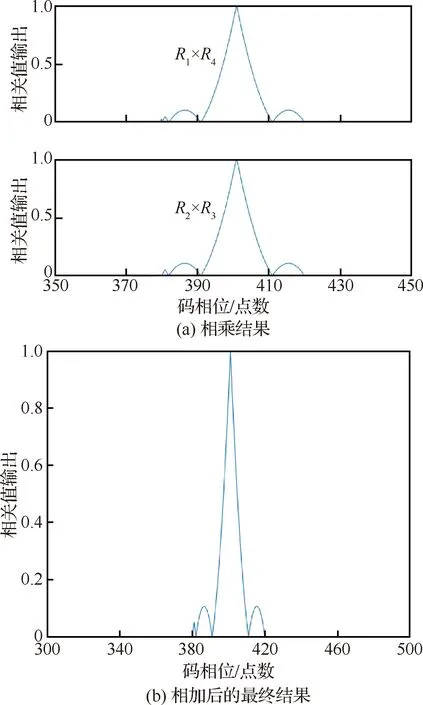
图5 BOC(2，1)重构后的相关函数Fig.5 Reconstruction of BOC(2,1) sub-correlation function

1.4 快速算法

由式(10)所示的移位相乘法，有效消除了旁峰对捕获的影响，但重构结果并未完全消去旁峰，且实现复杂，存在调制阶数为奇数时效果不好的局限性。为解决该算法存在的问题，基于上述移位相乘法提出了一种快速算法。

图6为快速算法原理框图。在图3中，对于分离得到的子自相关函数，取第1个和第个，即()和()，将其相乘得到单峰，以此来降低运算的复杂度，获得较快的处理速度，同时解决了移位相乘法在BOC信号调制阶数为奇数时不适用的局限性。此时得到的结果仍和移位相乘法一样，并未完全将旁峰消去，令()和()乘积为1，观察结果可知，只需将1取绝对值，再和1相减，原来存在的旁峰即可正负相抵消，完全消去，快速算法最终的重构函数为

=|1|+(-1)

(18)

根据式(18)得到图7所示的最终检测量为

(19)

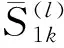
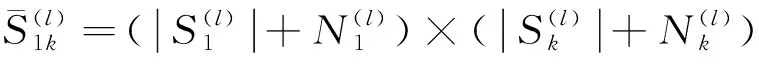
(20)

结合两者优势，快速算法具有比移位相乘法更低的复杂度、更快的处理速度和旁峰消去能力。该算法通过牺牲一部分能量来换取更低的运算量，但其最终输出相当于将主峰叠加，减少了能量的损失，对于低阶BOC调制信号的情况，该算法能量反而有所提高。图7为以BOC(2,1)为例的快速算法结果图。

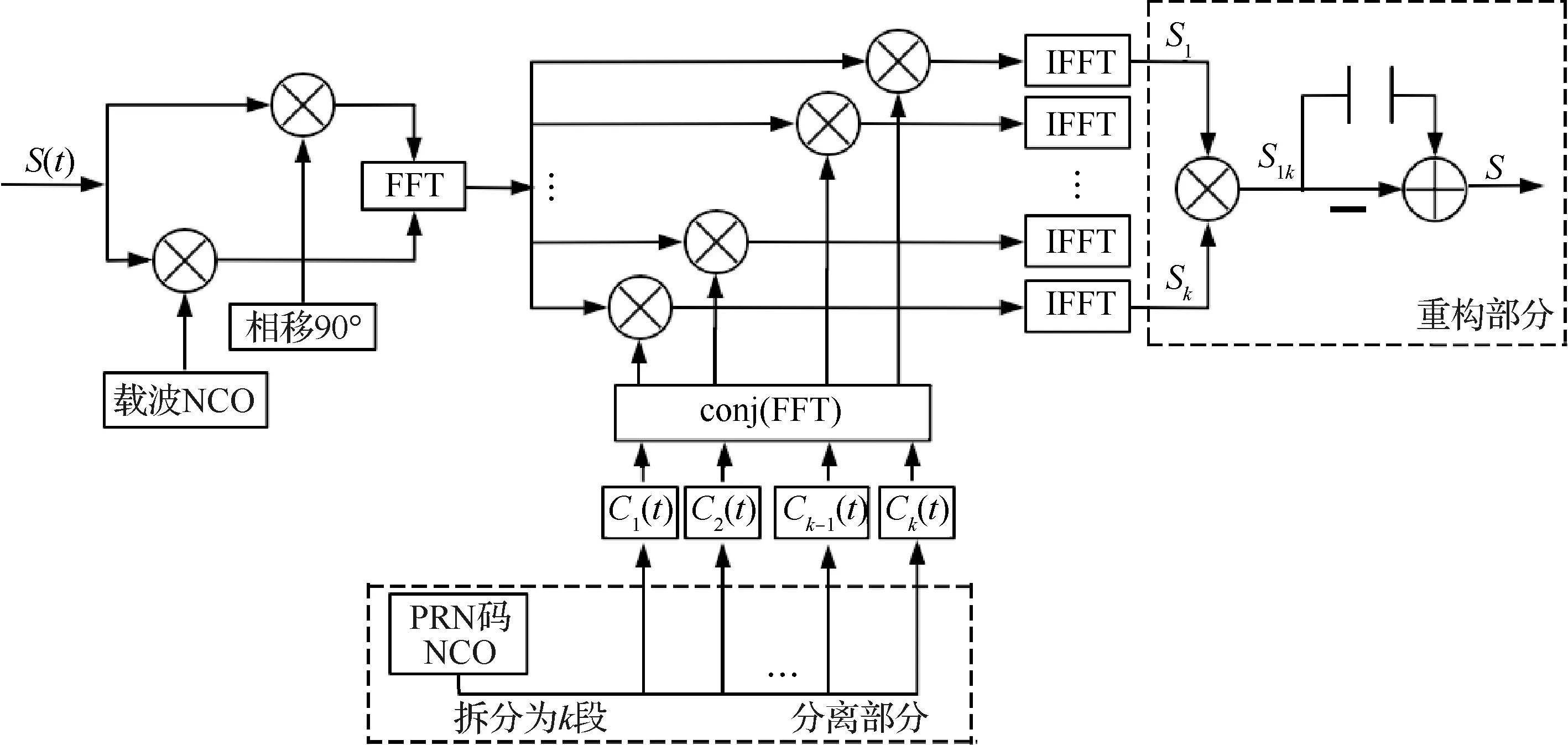
图6 快速算法原理图Fig.6 Schematic diagram of fast algorithm

图7 快速算法相关函数重构结果Fig.7 Reconstruction results of sub-correlation function of fast algorithm

虽然本文提出的移位相乘法及其快速算法均以正弦型BOC调制信号为例分析，但同样适用于余弦型的BOC调制信号。对于余弦型BOC调制信号，当其调制阶数为偶数时，移位相乘法及快速算法与正弦型BOC调制信号消除旁峰的方式基本相同。但是对于奇数阶数的BOC调制信号，其子相关函数个数为奇数，而移位相乘法需将子相关函数分为两组，此时只能使用快速算法，消除旁峰的方式与偶数阶数BOC调制信号相同。

2 检测统计量分析

2.1 移位相乘法检测统计量

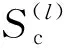
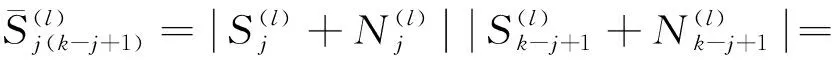
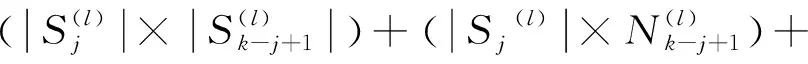
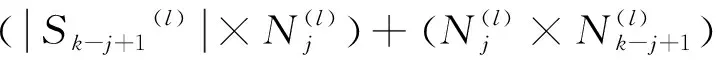
(21)

将式(21)整理得到3部分，纯信号项、纯噪声项以及信号与噪声的交叉项，分别如下所示。

纯信号项：

=|()|×|-+1()|

(22)

纯噪声项：

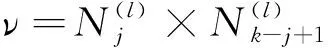
(23)

交叉项：

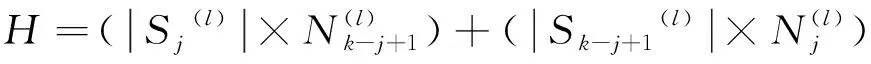
(24)

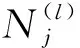
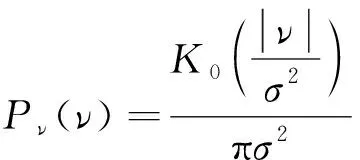
(25)

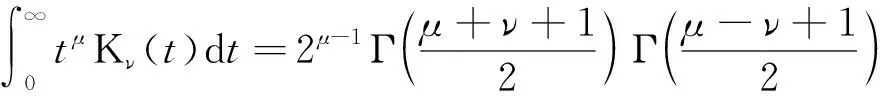
(26)

式中：K(·)为第二类阶修正贝塞尔函数；Γ()为伽玛函数；的方差为

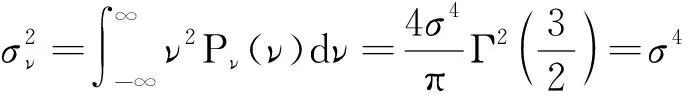
(27)

根据中心极限定理，当数据段数的值很大时，最终检测量中的纯噪声项为类似高斯变量，近似服从正态分布，其方差如式(28)所示：

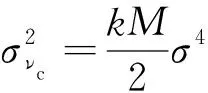
(28)

信号与噪声的交叉项相当于高斯噪声乘以一个常数，其仍然服从高斯分布，因此的方差为

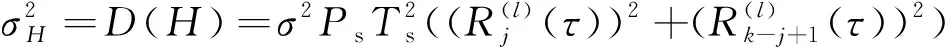
(29)

最终检测量中的交叉项方差为

(30)

综上是高斯噪声与常量的累加，亦服从均值为()、方差为()的高斯分布，的均值和方差如式(31)、式(32)所示：

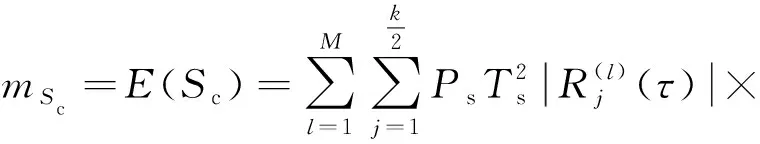
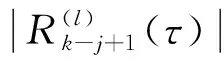
(31)

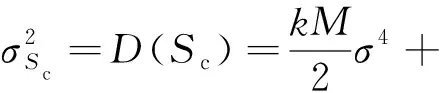
(32)

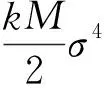
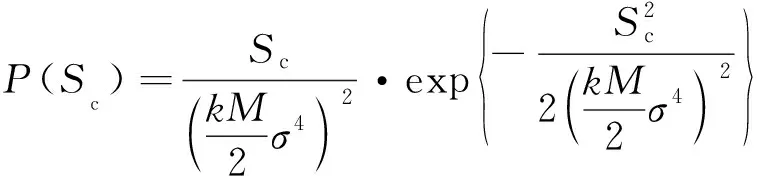
(33)

虚警概率可表示为

(34)

式中：为检测门限值。根据奈曼皮尔逊准则，可计算得条件移位相乘法的门限值。

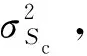
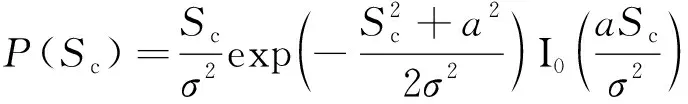
(35)

式中：为信噪比；I()表示第一类零阶修正贝塞尔函数。因此检测概率为

(36)

同理可得条件下移位相乘法的门限值。

2.2 快速算法检测统计量

对于快速算法，按照式(21)～式(36)的分析方法，对式(19)所示的检测量分析有：

在的条件下，的概率密度函数为

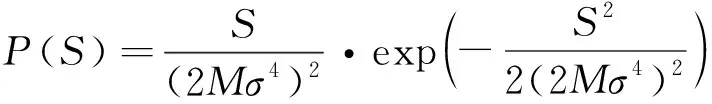
(37)

虚警概率为

(38)

在的条件下，的概率密度函数为

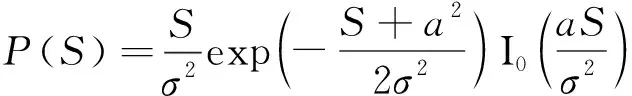
(39)

检测概率为

(40)

根据奈曼皮尔逊准则即可得到和条件下的快速算法门限值。

2.3 性能分析

检测概率是反映捕获算法优劣最好的指标。与传统BPSK信号检测性能的影响因素不同，BOC信号的检测性能由噪声和旁峰共同影响。为了从理论上证明本文算法的有效性，根据2.1节和2.2节分析得到的门限值和检测概率表达式，绘制信噪比与检测概率关系图，分析本文算法的检测性能。图8为通过蒙特卡洛法模拟5种算法在相同条件下，BOC(2,1)的检测概率对比，设置仿真环境的非相干积分时间为1 ms，虚警概率为=001，码长为2 046个码片，采样率为81.84 MHz，信噪比范围为[25，45] dBHz。捕获判定的依据为不同信噪比条件下，最大峰值出现的位置与码相位时延大小之间的误差在±1/4个码片内。

从图8中可以看出，本文算法检测概率较3种传统算法有明显优势。从检测概率的角度来看，本文算法在相同信噪比条件下，检测概率均高于3种传统算法。假设检测概率=90%，移位相乘法在信噪比约37 dBHz时可达到相应的检测性能，快速算法所需信噪比约为37.5 dBHz，而ASPeCT法需在41 dBHz左右,本文算法捕获性能优于ASPeCT法约4 dB和3.5 dB，且优于SCPC和BPSK-Like法3 dB、2.5 dB和6 dB、5.5 dB。原因是本文算法在保留BOC信号窄相关峰特性的同时，有效抑制了旁峰，ASPeCT法不能很好的抑制旁峰的影响，且对于高阶BOC信号其不再适用，而BPSK-Like法和SCPC法虽然达到了抑制旁峰的效果，但两者均未保留窄相关峰特性。在相同条件下，噪声更容易使相关峰值在±1/4个码片之外高于预设的门限值，降低捕获性能；移位相乘法相较快速算法虽具有更多的能量，但并未将旁峰完全消去，快速算法在完全消去旁峰的同时，其最终输出相当于将主峰进行叠加，减少了能量的损失，理论曲线表明快速算法性能与移位相乘法相当，两者差距在0.5 dB以内。

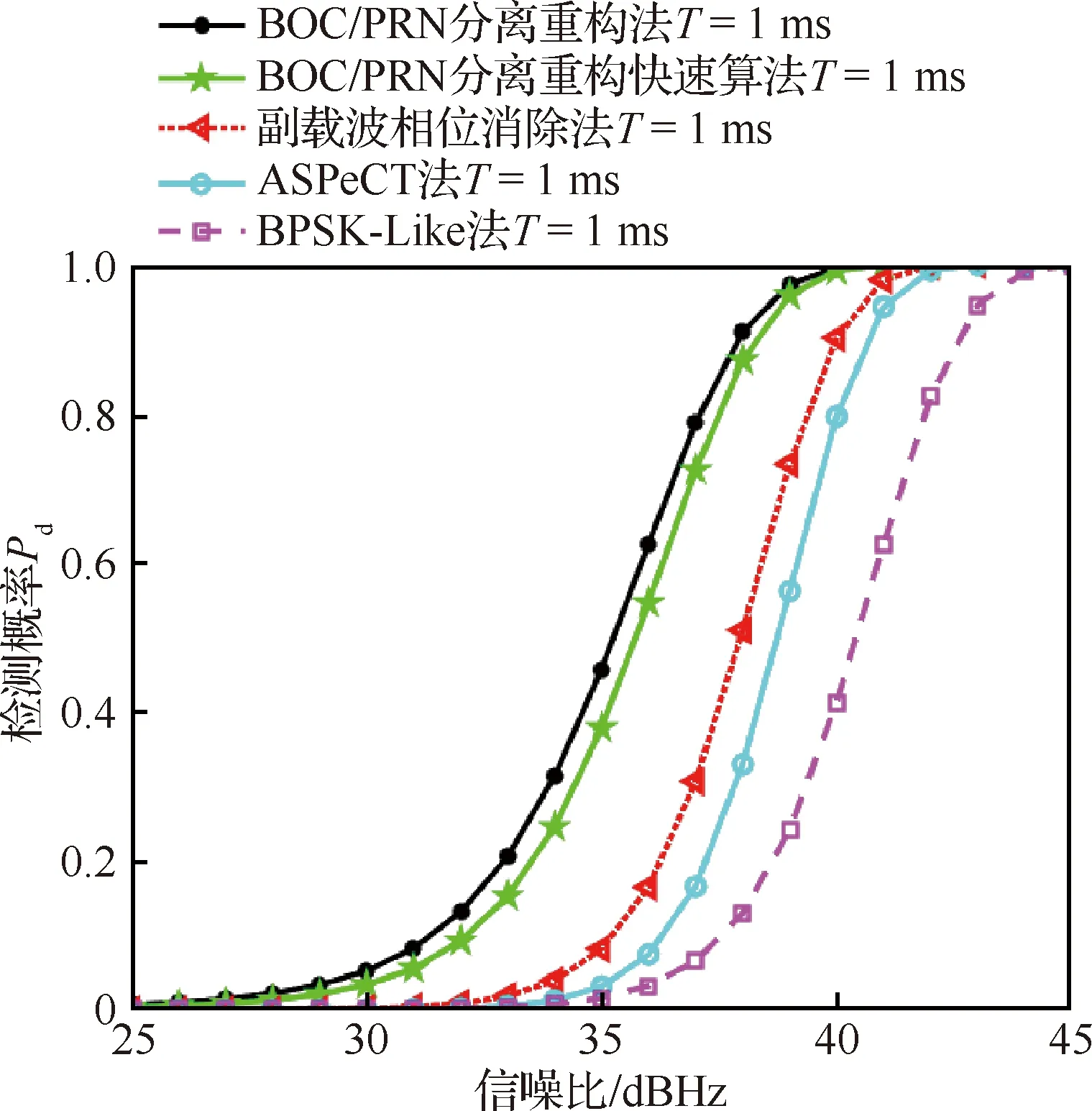
图8 检测概率与信噪比的关系Fig.8 Relationship between detection probability and carrier to noise ratio

3 实验结果与分析

为了验证本文算法的性能，根据第1、第2节部分的算法原理和理论分析，基于MATLAB平台对算法进行仿真实验，设输入中频信号的频率=4.092 MHz，码长为2 046个码片，信噪比为-25 dB，采样率= 81.84 MHz，积分时间= 1 ms，设置多普勒频移= 3 000 Hz，多普勒频率的搜索范围为[-10，10] kHz，频率搜索步长为500 Hz，码相位延迟= 401采样点。给出了本文算法的捕获仿真结果，同时对比了本文算法与SCPC、ASPeCT以及BPSK-Like法的二维捕获结果，分析本文算法的旁峰消除效果。

3.1 三维仿真结果

以BOC(2,1)信号为仿真信号源进行捕获，图9(a)为移位相乘法三维捕获结果图，图9(b)为快速算法三维捕获结果图。

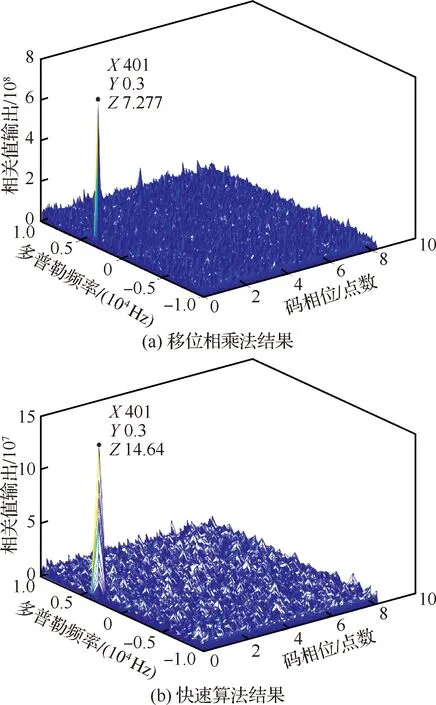
图9 三维捕获结果Fig.9 The 3D acquisition result

由上述实验结果可知，以最大相关峰值作为搜索门限，本文两种算法捕获多普勒均为3 000 Hz，码相位延迟为401个码片，捕获估计参数与预设参数一致，验证了本文算法的可靠性。

3.2 二维仿真结果

图10为5种算法标准化后的旁峰消除效果的二维对比图。从结果图可以明显看出，ASPeCT法并没有很好的旁峰消除能力，其结果存在两个峰值较高的旁峰和多个较小的旁峰，主峰宽度为20个采样点。随调制阶数的增大，ASPeCT法中的旁峰数量不断增多，不再适用于BOC信号捕获。移位相乘算法虽然并没有将旁峰完全消去，但仅存在两个峰值较小的正值旁峰，相较主峰峰值，影响基本可以忽略，在相同码相位误差范围内估计，ASPeCT法旁峰检测量的值为0.548，移位相乘法中旁峰检测量的值为0.105 7，ASPeCT法的误捕概率高出移位相乘法约7 dB，而主峰宽度与ASPeCT相当，为20个采样点。SCPC、BPSK-Like和快速算法均消去了旁峰，但SCPC和BPSK-Like没有保留BOC信号的窄带特性，主峰宽度固定为80个采样点，即两个码片宽度，不满足BOC信号高精度捕获要求；而快速算法在将旁峰完全消除的同时，还保留了主峰的窄带性，其宽度和ASPeCT法、移位相乘法相同。在主峰宽度方面本文算法同ASPeCT法明显优于SCPC、BPSK-Like法，且本文算法随着调制阶数增大，主峰宽度会越窄；在旁峰消除方面，快速算法完全消去了旁峰且保留了窄带特性。

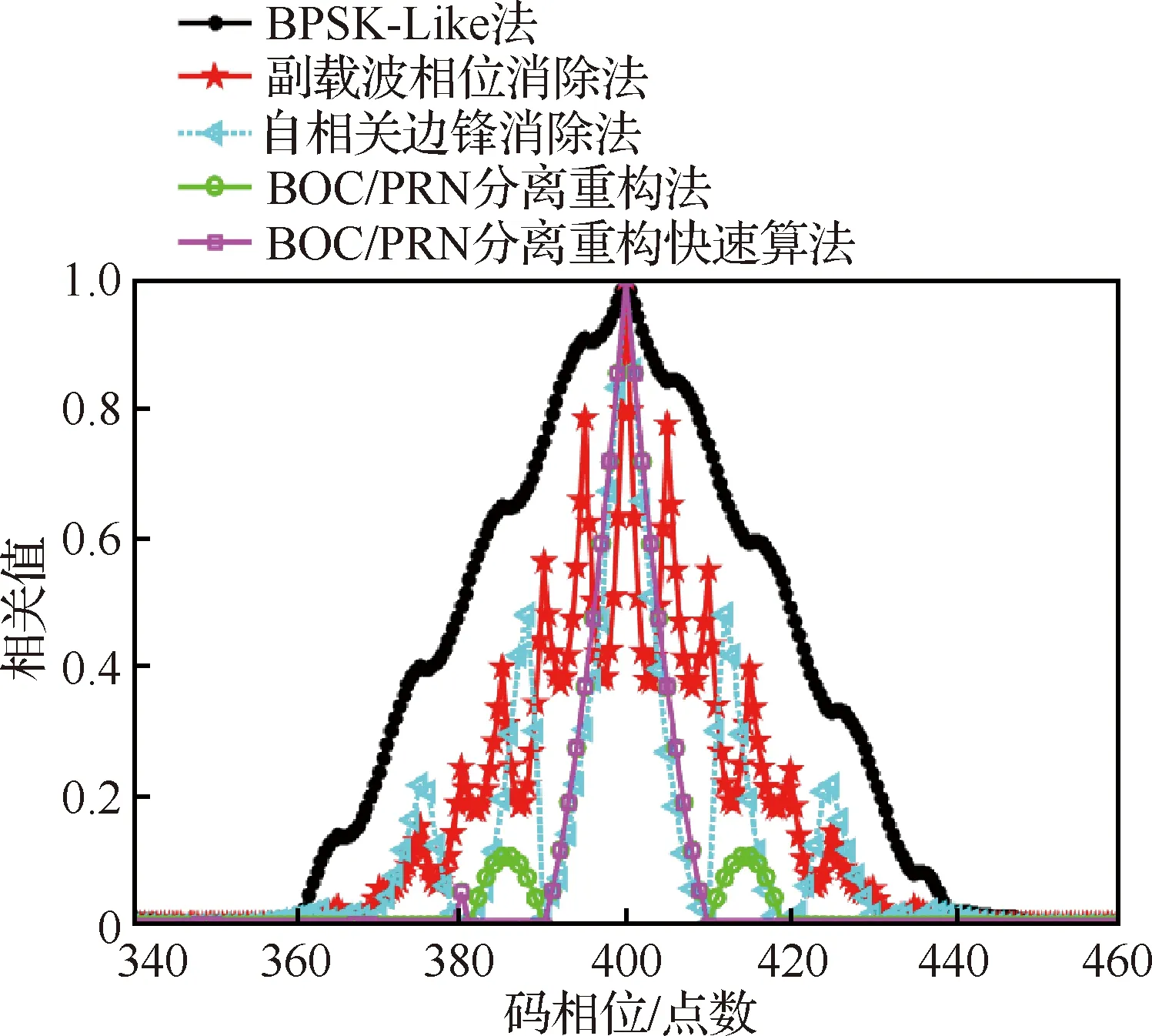
图10 5种算法二维捕获对比Fig.10 2D acquisition result of five acquisition methods

3.3 算法复杂度

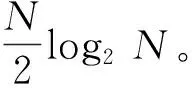
积分时间=1 ms，共81 840个采样点，根据多普勒检测范围和步进可计算得到41个频点。本文提出的快速算法经2次复数乘法运算、1次实数相乘运算和1次实数加法运算，再经5次FFT得到最终检测结果；ASPeCT法的运算量为，8次FFT运算、4次复数乘法运算、2次实数相乘运算；BPSK-Like法的运算量为，4次复数乘法运算、2次实数相乘运算、8次FFT运算；SCPC法则是5次FFT运算、2次复数乘法运算、2次实数相乘运算。

一般来说，一次复数乘法可以分解成4次实数乘法和3次实数加法运算，一次复数加法等同于两次实数加法运算，结合式(41)、式(42)可得5种算法的总运算量。表1为5种算法捕获过程中的计算复杂度对比。

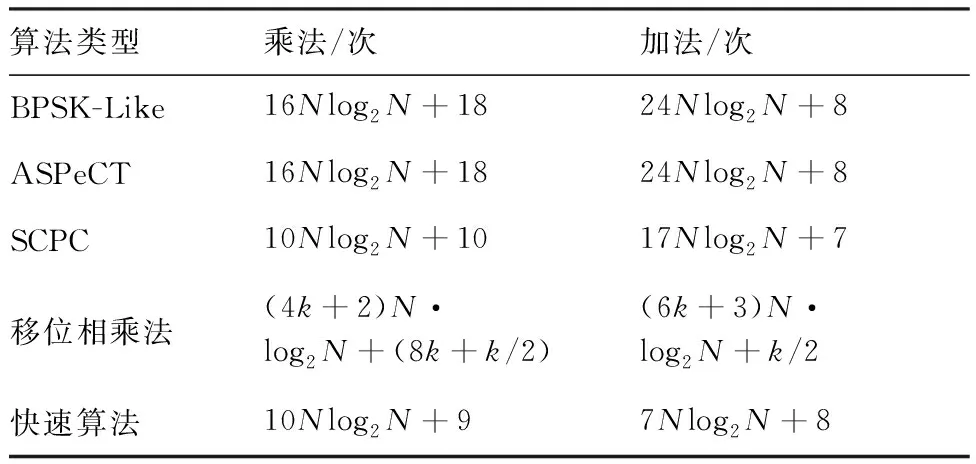
表1 5种算法运算量对比Table 1 Comparison of calculation between five algorithms

若假设一次乘法运算时间和一次加法运算时间均为，将实际参数带入到表1中，可以得到实际的乘法和加法运算次数。以=81 920点FFT为例，比较发现快速算法的计算量为ASPeCT和BPSK-Like算法的58.54%，效率提高了约40%；而与SCPC相比，两者运算量一样。移位相乘法在调制阶数为2时，运算量和SCPC以及快速算法相同，但随调制阶数增大，其运算量要远高于其他四种算法，最为复杂。