基于自适应笛卡尔网格的飞翼布局流动模拟

2022-09-07陈浩华如豪袁先旭唐志共毕林

航空学报 2022年8期

陈浩，华如豪，袁先旭，唐志共，毕林,*

1.中国空气动力研究与发展中心空气动力学国家重点实验室，绵阳 621000 2.中国空气动力研究与发展中心计算空气动力研究所，绵阳 621000

网格生成技术是计算流体动力学(CFD)不可或缺的重要组成部分。计算网格的合理设计和高质量生成是数值模拟的前提条件，直接影响数值模拟过程的稳定性和数值计算结果的精准度，关乎计算的成败。在CFD计算中，网格生成需要频繁的人机交互，是人工工作量最大的部分，且网格生成质量严重依赖用户经验，是制约CFD效率的主要瓶颈。美国Sandia国家实验室的研究表明，前处理过程占据了数值模拟实践中总用时的90%，而网格生成相关的步骤独占总用时的76%。

目前，网格生成技术主要有3类：贴体结构网格、非结构网格和非贴体的笛卡尔网格。相对前两者而言，笛卡尔网格在自动化程度方面有着天然的优势，且易于捕捉流场精细特征，能够保证网格质量。然而，对于自适应笛卡尔网格方法而言，其普及性和推广度不如传统的结构和非结构网格，很大程度上是因为其非贴体特性引起的高精度模拟时网格规模过大，导致计算量和存储量的急剧增加，计算成本可能难以接受，这在当前的计算机硬件条件下仍然是不容忽视的。例如，对于工程型号问题中遇到的复杂构型，往往存在精细和跨尺度结构，此时使用自适应笛卡尔网格时，必须通过足够次数的自适应加密，高保真地刻画模型边界信息，通常会比贴体类网格花费数倍的网格量，甚至有量级上的差距。如果复杂外形存在运动或变形，对于笛卡尔网格带来的计算量过大的问题就更加凸显，计算周期会很长甚至难以接受。

因此，对于自适应笛卡尔网格方法而言，在实现工程实用化的前进道路上，还需要聚焦到上述技术瓶颈，重点解决网格规模控制、网格生成高效算法设计、非贴体壁面高保真处理等关键问题，以实现大规模自适应笛卡尔网格完全自动化高效生成和复杂外形/流场高效高精度地计算，为缩短CFD计算周期，实现工程型号快速迭代设计提供技术支撑。本文正是以此为出发点，对黏性自适应笛卡尔网格方法进行发展，并开展复杂构型流动问题的应用研究。

本文所选取的应用对象为小展弦比飞翼布局飞机，其采用翼身融合的全翼式设计，取消了平尾和垂尾，整体上具备较好的气动特性和隐身特性，是下一代超声速高性能战机的理想构型。由于其气动布局和常规战斗机存在较大差异，目前对其气动特性的认知仍然不足，需要进一步开展研究。

由于小展弦比飞翼飞机构型的特殊性，存在较多的尖点结构，会给贴体网格的高质量生成带来困难。而采用自适应笛卡尔网格方法可自动化生成高质量的空间网格，避免了上述问题并能对空间流动特征进行精细化模拟。目前，从公开发表的文献来看，尚未见基于黏性自适应笛卡尔网格的小展弦比飞翼飞机流动数值模拟。因此，本文选取该构型进行模拟研究，考核本文的黏性自适应笛卡尔网格方法，并深入探究其气动力特性。

1 自适应笛卡尔网格生成技术

自适应笛卡尔网格生成的基本流程如图1所示，图中：为自适应加密时间长;Δ为时间步长。

1) 读取STL(STereoLithography)格式的几何模型数据文件，并构造物面离散单元的二叉树，方便快速检索。

2) 设定计算域，划分初始网格。

3) 构建笛卡尔网格数据结构，建立网格信息存储和链接关系(邻居关系、父子关系、兄弟关系)。

4) 判断网格单元类型(物面内网格单元、物面外网格单元以及物面相交网格单元)。

5) 对于物面相交单元加密一定的次数，直到达到模型保真度的需求。

6) 对于加密过程中新出现的网格单元，重复4)和5)。

7) 对于通过上述加密得到的网格进行光顺优化。

8) 进行初步流场计算，在进行到一定时间步后，根据流场解特征进行进一步自适应，以使空间网格分布更合理。

图1 自适应笛卡尔网格生成流程Fig.1 Flowchart of adaptive Cartesian mesh generation procedure

在上述步骤中，网格数据结构尤其关键，直接决定了网格信息查询效率；网格单元类型判断方法则对网格生成的准确度有着重要影响；几何自适应和流场自适应技术是本文网格自适应加密和粗化的依据；此外，对于非贴体物面边界的处理是构建笛卡尔网格数值求解器的重要前提。下面，分别对上述技术方法展开介绍。

1.1 网格数据结构

叉树结构是自适应笛卡尔网格使用最多的数据结构形式，其易于自适应的特点与笛卡尔网格天然契合。然而，由于笛卡尔网格自适应后是分层式的组织框架，不同层的网格之间的数据交互往往需要递归查询，甚至遍历整个树结构，导致计算量较大，给网格生成和流场计算的高效性带来阻碍。为此，发展了一种全线程树数据结构(Fully Threaded Tree，FTT)。

FTT最初是由Khokhlov提出，该方法的基本思想是：在传统四叉树或八叉树的基础上，将其闲置的叶子节点利用起来，存储指向邻居单元的父节点的指针，以建立它将叉树数据结构中叶子节点闲置的指针利用起来，指向邻居单元的父单元，从而构建邻居单元之间快速交互的“线程”。这种方法不仅可以提高网格生成、信息调用的效率，还能够提高网格存储的利用率。

为了进一步减少网格类型判断过程中相交信息的重复计算，提高网格生成的效率，发展了一种新型的FTT数据结构。该方法的思路是：在传统FTT数据结构的基础上，对于网格相交面元序号，进行动态存储。事实上，父子单元相交面元间存在“继承性”，即与子单元相交的面元肯定与父单元相交，基于这个原则，就可以把相交判断过程中面元检索范围限制在很小的范围，大幅提高网格相交判断的效率，进而提高整体的网格生成效率。

基于上述方式，所构建的笛卡尔网格数据结构如图2所示，Oct和Cell之间的组织关系如图3所示。可以看到，除了传统FTT基本的Oct模块(包含层次OctLv、中心坐标(,,)、父指针OctPr、各方向邻居的父单元OctNb(6)等信息)，还添加了动态数组OctTC(：)，用于存储与笛卡尔网格相交面元的序号。OctCh代表存储的子单元；代表流动矢量。当存在相交面元时，该数组被分配内存和赋值；在完成子单元的计算后，父单元的存储数组就会被释放内存，以减少重复存储。

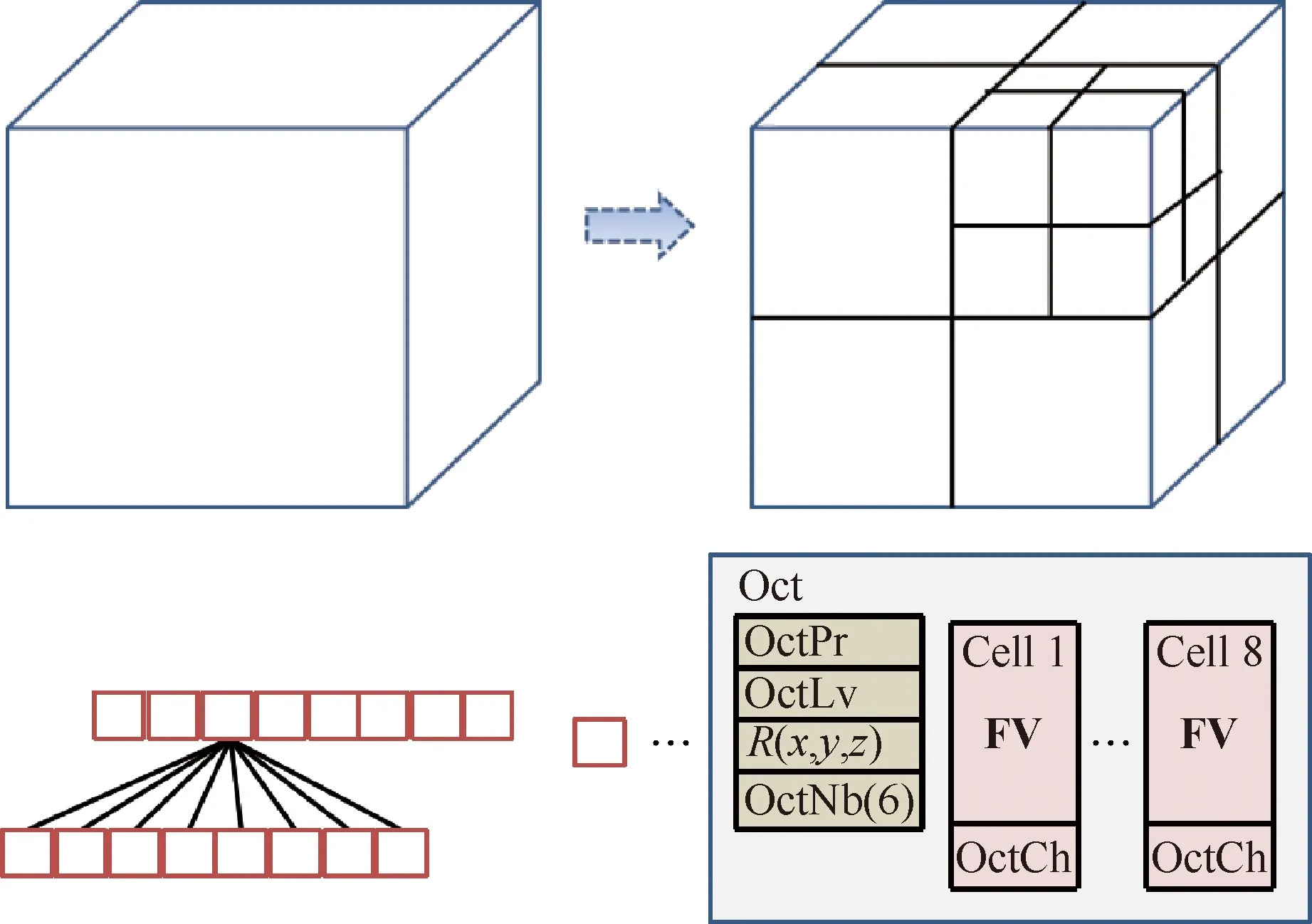
图2 FTT数据结构Fig.2 FTT data structure

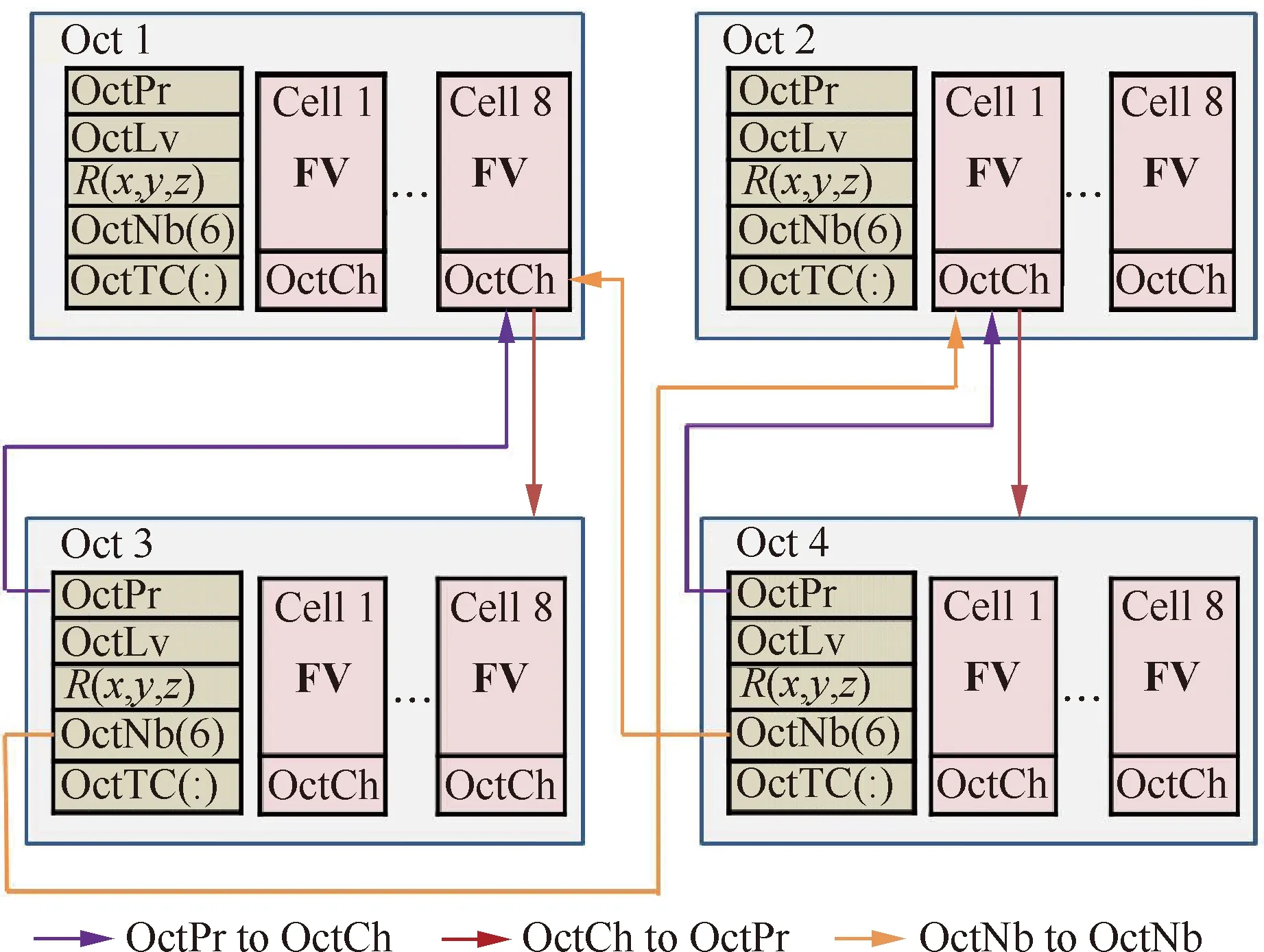
图3 FTT数据结构中Cell和Oct的关系[14]Fig.3 Relationship between Cell and Oct in FTT[14]

1.2 射线相交判断

对于笛卡尔网格单元类型的判断，最常用的方法是射线相交方法。该方法的基本思路是：通过计算过目标点的射线与封闭物面的相交点数目，来确定目标点在物面的内外(奇数时在内部，偶数时在外部)。这种方法简单高效，但是存在特殊情况，如射线经过几何拐点时，若还按照上述判断方法，就会出现错误。因此，有必要准确识别射线经过拐点的情况，如图4所示。图中：、代表正常的射线；1、2代表经过拐点的错误射线。

图4 基于射线相交方法判断目标点位置[14]Fig.4 Illustration of point inside or outside polygon using ray-casting method[14]

针对上述问题，发展了一种奇点检测算法，可以有效识别上述情形。将其与射线相交方法结合，可保证网格点类型判断的准确性。奇异性检测算法的思路是：通过射线方向与拐点位置几何离散单元法向之间夹角的关系，来识别射线对应的目标点在几何内外。

以图5为例，目标点在封闭几何外部所满足的判据为

cos〈,〉·cos〈,〉>0

or cos〈,〉·cos〈,〉>0

〈,〉=〈,〉=>0

目标点在封闭几何内部所满足的判据为

cos〈,〉·cos〈,〉>0

or cos〈,〉·cos〈,〉>0

〈,〉=〈,〉=>0

上述公式的具体论述过程参照文献[14]。本文针对射线经过封闭几何拐点的情况，以二维几何问题为例，具体处理方法如下：

1) 在射线与几何离散单元存在交点时，判断该交点是否为该几何离散单元的端点或边缘点，若是，即射线经过封闭几何拐点。

2) 计算该射线方向，几何离散单元法向。

3) 通过上述判据公式，结合图5，判断目标点在封闭几何的内部还是外部。

图5 射线过拐点的情形[14]Fig.5 Illustration of ray passing inflection point[14]

通过上述步骤，可识别射线经过封闭几何拐点对应的目标点位置情况，避免传统射线相交方法因相交次数计数不准带来的误判。

1.3 网格数据结构

在完成网格类型的判断后，需要根据几何特征加密一定的次数，达到几何信息保真度需求。具体来说，主要包括相交单元自适应和曲率自适应，即分别对于与物面相交的网格单元和曲率变化较大位置的网格单元加密一定的次数，一般后者是在前者的基础上进行的。在针对具体流动问题进行几何自适应加密时，还会考虑边界层网格高度的要求，来确定具体的加密次数，以使得最大壁面网格高度满足约束条件。

对于笛卡尔网格而言，在加密后，相邻层次的粗网格与细网格的尺寸之比值恒定为2，即使在附面层内。这种网格尺寸的大比例变化，会影响近壁面流动模拟的精度和稳定性。针对上述问题，本文借鉴贴体结构网格对于边界层流动特征捕捉的优势，引入虚拟层技术进行近壁面网格的优化，如图6所示。首先根据物面外形数据点沿壁面法向射线方向按照一定规律在边界层内布置一系列点、、、…，由第一层数据点生成初始虚拟面，然后设定虚拟物面沿壁面法向距离层进比例：

式中：为第层网格的高度。该比例的设定借鉴贴体结构网格在边界层内的网格分布特点，得到边界层内多个距离变化均匀的虚拟面，其距离排布类似贴体结构网格。笛卡尔网格单元的加密次数和层级就结合这些虚拟物面确定。

图6 虚拟层方法示意图Fig.6 Illustration of virtual layer method

1.4 流场自适应

为了使网格分布更合理，以节省网格量和精细捕捉流动结构，需要根据流场解的特征进行进一步的自适应加密或粗化。

初始网格的分辨率往往不足以精细刻画流动特征，合理有效的流场解自适应判据是开展流动自适应的前提。根据不同的流动特征，往往需要建立对应的特征识别准则。一般来说，流动的间断区域，如激波，需要速度或压力的梯度进行识别；而涡结构集中的区域，用涡量、速度的旋度等识别效果更好。针对本文的研究对象，即低速不可压缩情况下的飞翼流动模拟，为涡旋结构主导，不存在激波等间断特征，因此，本文选用的是以速度旋度作为流动自适应判据。

在笛卡尔网格框架下，单元cell的速度旋度可表示如下：

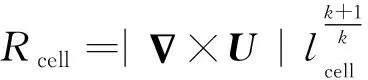
式中：为速度；为网格单元cell的边长，三维情况下=3。

相应的速度的旋度的标准差为

式中：为计算域内所有的网格单元总数；为单元cell的速度的旋度的标准差。具体判据如下：

式中：、为经验系数，需要针对具体的流动问题给出。

2 物面边界条件

基于浸入边界方法处理非贴体笛卡尔网格物面边界的基本思路是：

1) 首先，确定判断物面附近计算模板点是否在物面内部，并对内部的计算模板点标记为虚拟单元(Ghost Cell)。

2) 对于虚拟单元关于物面边界取参考点。

3) 通过临近单元插值方法获取参考点的流场值。

4) 通过物面无滑移、无穿透条件建立虚拟点和参考点的对应关系。

5) 考虑物面曲率的影响，进行曲率修正。

以图7为例，虚拟点在流场中的参考点为，为到壁面投影点的距离。对于参考点的取法，传统方式一般是取关于物面的镜像对称点。这种方法虽然简单，但是在虚拟点很靠近物面的时候，参考点也会离物面很近，导致其插值用到的临近单元会有部分在物体内部，这会对其流场值得计算带来误差。本文的方式是借鉴Forrer和Jeltsch的取法，将参考点沿对称线延长一个当地网的长度，确保临近插值单元均在

图7 非贴体物面处理方法Fig.7 Processing method of non-body-fitted wall

流场之中。Forrer和Jeltsch的研究表明，这种位置取法可以提高边界附近计算的稳定性，而且并不会降低非贴体物面模拟的精度。

参考点流场值通过邻近单元插值获取，以参考点为例，其邻近的4个单元结点分别记作、、、，则其流场值为

式中：、、、分别为点到网格点、、、的距离。

虚拟点和参考点的关系式如下：

式中：为气体常数。

3 数值方法

采用三维守恒型Navier-Stokes方程作为可压缩黏性流动的控制方程，即

式中：和分别为来流马赫数和雷诺数；为守恒变量；、、代表无黏通量；、、代表黏性通量。

对于Navier-Stokes方程的数值离散方法是通过张涵信院士建立的NND格式进行无黏项的离散，以及通过中心差分方法进行黏性项的离散，在避免出现非物理振荡的同时，可实现较高精度的捕捉激波、剪切层、接触间断等流场结构及现象。

以方向上的变量为例(其他方向的形式类似)，采用NND格式的无黏通量空间离散如下：

()=+12--12

对于时间的推进使用的是显式推进方法。显式方法不需要进行大量的矩阵运算，存储量也较小，同时方法的建立和程序实现比较简单。为了保证所构建的全离散格式的TVD性质，本文选取的是具有TVD性质的Runge-Kutta型二阶时间离散格式，如下：

对于自适应笛卡尔网格方法而言，在构建数值离散框架时，需要考虑网格自适应带来的非均匀、粗细过渡的特征，即悬挂网格的处理。其思路是通过插值重构的方式，构造需要的计算模板点，具体可参考文献[27]，这里不再赘述。

4 结果和讨论

本节选取小展弦比飞翼布局飞行器这一复杂构型飞行器，运用本文发展的自适应笛卡尔网格技术开展模拟研究。该飞行器采用隐身布局，同时气动性能较好，在作战飞机设计方面有着广泛的应用前景。该几何标模的外形如图8所示，经由国内多个研究机构联合开展了数值模拟和风洞试验。本文采用该标模来考核验证本文的笛卡网格生成技术和数值求解器，并开展笛卡尔网格自适应技术对于小展弦比飞翼布局飞行器气动力特性影响规律的研究。

图8 小展弦比飞翼布局风洞模型Fig.8 Wind tunnel model of low aspect ratio fly-wing aircraft

来流马赫数为0.2，静温和静压分别为288.15 K 和101 325 Pa，参考实验设计，选取来流攻角分别为=20°、24°、28°、32°、36°、38°、40°、42°、44°、48°、52°，无侧滑角。初始几何自适应网格如图9所示，其中物面网格49 026，为三角形离散单元，经几何自适应加密后，空间笛卡尔网格数目为2 259 042。

图9 几何自适应笛卡尔网格Fig.9 Geometry adaptive Cartesian mesh

图10和图11为流场计算结果的流动自适应网格和压力分布云图、流场流线。可以看出，本文的自适应笛卡尔网格技术能够对于空间流场的特征结构进行很好的捕捉，并进行自适应加密，确保重要流动结构的高精度模拟。网格自适应区域主要集中在翼尖和尾尖牵引的尾流区，同时对于大攻角分离区的流场梯度变化也能很敏锐的捕捉。通过截面图，可以看到在背风区分离涡也有很好的自适应效果。相对28°攻角、40°攻角时在网格分布上展现出了更复杂的分布特性，考虑是由于大攻角流动分离引起的涡结构演化导致的。

图10 来流攻角为28°和40°时的压力和网格分布Fig.10 Pressure and mesh distribution at α=28°，40°

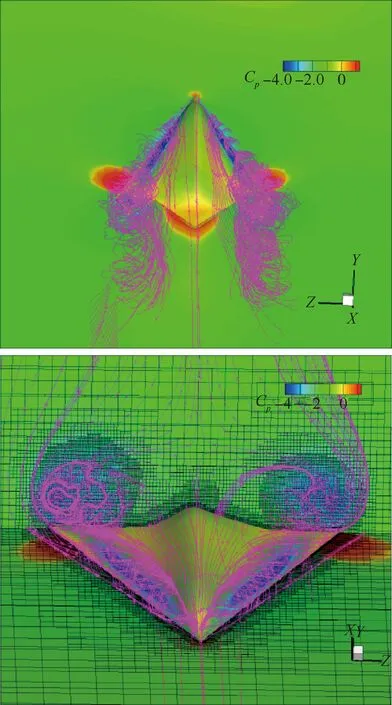
图11 来流攻角为28°时流线和涡结构自适应网格示意图Fig.11 Stream lines and adaptive mesh around votex at α=28°

图12为自适应笛卡尔网格方法得到的不同攻角下的升力系数，并与不同风洞试验数据的对比，呈现了较好的吻合度。可以看出，FD9、FL8、FL12这3组试验结果给出的失速攻角在40°附近，而本文计算结果在38°附近。在计算结果中，升力系数在40°时明显下降，通过对比两者的流场云图可以看出，在40°攻角时，由于大攻角分离，分离再附区减小，涡结构演化时横向流动变强，使得飞行器背风区的压力降低，从而导致升力系数减小。

图12 升力系数的计算结果与风洞试验结果对比Fig.12 Lift coefficient comparison of calculated and experimental results

对于自适应前后流场特性和气动力特性的对比研究，从图13和图14中攻角为28°和40°上表面的压力分布在自适应前后的变化可以看出，在自适应后，攻角为28°的状态下，飞行器背风区上表面的低压区更大，这将导致更高的升力系数。而在40°攻角状态下，背风区压力分布较复杂，上述规律并不明显。自适应对背风区涡结构有着更高精度的捕捉，降低了分离涡的数值耗散，呈现了更大的低压背风区，使得升力系数更高。

图13 不同攻角下自适应前后压力系数对比Fig.13 Pressure coefficient comparison before and after adaptation at different angles of attack

图14 自适应前后涡结构附近网格和流场云图对比结果Fig.14 Mesh and pressure contour comparison before and after adaptation

下面结合涡量图进一步对比网格自适应前后对于流动结构的捕捉能力。从图15中可以清晰看出，在不添加网格自适应时，背风区的流动分辨率很低，无法清晰辨识出涡结构，只能看出大致轮廓。并且在尾部离物面较远处，由于笛卡尔网格粗细不均，导致出现了压力云图的间断。而在引入网格自适应后，对于背风区分离流动的精细涡结构都可以较清晰的捕捉和呈现。本文中采用了NND格式和中心差分格式进行空间离散，数值格式耗散较小，而自适应技术的引入，又能够充分保证流动细节较多的位置的网格密度(见图10，图14～图16)，从而能够较高分辨率地捕捉流场涡结构。此外，还可以看出不同来流攻角下的背风区涡结构演化特征。在来流攻角为28°时，能看到完整的涡条结构，在靠近尾部时才破碎；在来流攻角为40°时，背风区流场基本处于完全破碎的大分离状态，仅在靠近头部有较短、较细的涡条结构。

图15 自适应前后涡量图对比(α=28°)Fig.15 Comparison of vorticity contour before and after adaptation (α=28°)

图16 自适应前后涡量图对比(α=40°)Fig.16 Comparison of vorticity contour before and after adaptation (α=40°)

图17为自适应前后的升力系数、阻力系数以及俯仰力矩系数的对比数据曲线。可以看出，相比之下，自适应加密后与试验结果吻合更好。整体上，自适应加密会使计算结果值变大，这是因为对于背风区流动结构捕捉更精细，使得飞行器上表面的低压区较大，结合前面的网格自适应图和压力云图可以清晰看出。在=38°以下和=40°以上，两者差别相对较小，并且与试验结果也较为接近；在=38°和=40°附近，即接近失速攻角时，差别较为明显。说明在低速大攻角状态下，空间流动结构模拟的精细化程度，对飞行器的气动力特性计算的精准度影响相对较大。尤其是对于俯仰力矩系数，在自适应后与试验结果吻合度很好，尤其是在攻角较小时，纵向静稳定度与试验基本相符。

图17 不同来流攻角的气动力系数计算与试验结果对比Fig.17 Aerodynamic force coefficient comparison between calculated and experimental data at different angles of attach

图18中选取攻角为40°状态下，在小展弦比飞翼不同展向的截面位置上的压力分布，并通过自适应加密前后的数据进行对比。由图可以看出，对于飞翼模型的下表面，即迎风面，表面压力系数分布在自适应前后几乎无变化，这是因为在迎风的高压面，流动梯度变化并不大，自适应起到的效果不明显。而对于流动梯度变化较大的背风区，流场涡结构较为复杂，是网格自适应集中加密捕捉的区域。这使得自适应后飞翼的上表面压力相对更低，从而导致升力系数变大，俯仰力矩变小。这与前面的数据对比结果相一致，并与图13中压力分布云图呈现出的规律相同。