基于改进多目标粒子群算法的土石坝基座体型优化研究

许 佳，孙奔博

(1.新疆寒旱区水资源与生态水利工程研究中心，新疆 乌鲁木齐 830000；2.郑州大学，河南 郑州 475001)

沥青混凝土心墙坝具有对地基条件适应性好，防渗性能强，方便就地取材、沥青心墙延展性好等优点[1]，在国内外水电能源开发中占有重要地位，是今后高土石坝最有力的坝型之一[2]。我国沥青混凝土心墙坝的建设虽然起步较晚，但是发展迅速，且广泛应用于新疆、四川、云南等地区。然而，由于我国西部区域大多位于印度洋板块和亚欧板块附近，这些高沥青混凝土心墙坝的坝址区域范围内地震频繁发生且强度高，一旦强震造成溃坝事故，引发地震次生灾害，将会严重威胁下游人民生命财产、社会稳定与基础设施安全。因此，优化改进高沥青混凝土心墙坝的极限抗震能力至关重要。

在含基座的沥青混凝土心墙坝中，不同基座体型和心墙厚度对大坝性能有较大影响，优化基座体型和心墙厚度对于提高大坝安全性和经济性有着重要作用。周扬等[3]以四川去学沥青混凝土心墙堆石坝为例，通过对比分析四种不同体型的混凝土基座，对原基座体型设计方案进行了优化；刘兆龙[4]通过分析不同混凝土心墙基座变坡脚的大坝应力情况，为大坝基座的优化提供依据。传统的体型优化方法[5-6]通过多个不同尺寸方案的对比分析，得出较优的体型优化方案。然而，采用传统优化方法时，若变量空间设置不合理、存在多个优化变量，则难以找到最优解，优化效果欠佳。因此，若能提出一种满足复杂条件下体型优化的方法，实现多目标优化设计，具有重要的现实意义。

粒子群算法作为新型群智能算法的一种，因其概念简单、收敛迅速、容易实现等优点应用广泛[7-10]，且成功应用于大坝相关优化研究中。王伟等[11]利用粒子群算法的优化能力确定统计模型的回归系数，建立了大坝安全预警评价模型，由预测值和实测值的对比表明该方法用于大坝安全监测领域是可行有效的；刘树峰等[12]通过粒子群优化算法反演了板桥大坝混凝土坝体、坝基的渗透系数，通过与实测值的对比表明使用该算法效果良好；钟登华等[13]建立了以高拱坝跳仓排序规则为变量，以优化施工工期、月浇筑强度、浇筑机械利用率为目标的优化模型，采用粒子群优化算法对该优化问题求解得到了综合最优的仓面排序方案；齐银峰等[14]基于改进粒子群优化算法对BP神经网络的初始权值和阈值进行优化，并将该方法用于大坝变形预测中，结果表明该方法预测精度高、收敛速度快；倪沙沙等[15]借助支持向量机耦合粒子群优化算法建立了大坝渗透系数反演模型，渗透系数反演结果合理。

目前关于土石坝体型智能优化的研究较少，且传统优化方法难以解决日益复杂的研究问题，鉴于此，本文针对沥青混凝土心墙坝的基座体型和心墙厚度，基于改进的多目标粒子群算法和FLAC3D有限差分软件，以坝体最大沉降、混凝土基座大主应力、心墙大主应力和坝坡安全系数为优化目标，以6个尺寸参数为优化变量，建立了沥青混凝土心墙坝基座体型和心墙厚度优化模型，进行多目标的大坝安全性优化研究，为土石坝尺寸优化提供新思路和新方法。

1 改进的多目标粒子群算法原理

单目标优化方法仅能优化单一参数，而随着研究问题的深入，仅优化一个变量难以满足研究要求，多目标优化方法因可同时优化多个参数而被广泛应用。在多目标优化问题中，各个目标函数间往往存在着相互制约的关系，即其中一个目标函数的提高通常以其他某个目标函数的降低作为代价，某个目标函数的最优解对于其他目标函数而言可能不是最优解甚至可能为最劣解。因此，在多目标优化问题中，很难使多个目标函数同时达到最优值，通常只能在多个目标函数间折中协调，尽可能使所有目标函数共同达到较优状态，因此，不同于单目标优化问题，多目标优化问题的解不是单一解而是一组解，该组解集称为Pareto最优解集，Pareto最优解所形成的曲面称为Pareto前沿。多目标优化问题可用如下数学模型描述[16]：

minf(j)={f1(j),f2(j),…,fu(j)}

(1)

(2)

式中:j为m维优化变量；f为目标函数，fq为第q个目标函数，在多目标优化问题中，应使u≥2；h为不等式约束条件；g为等式约束条件；h和g可根据具体研究需求取舍。

若存在目标函数最大化的问题，即max{f(x)}，可将其转为最小化问题min{-f(x)}，目标函数的最大化问题与最小化问题没有本质上的区别[17]。

多目标粒子群算法(Mutli-Objective Particle Swarm Optimization,简称MOPSO)[18]因简单易行，收敛速度快，设置参数少等优点，在多目标优化问题的研究中优势明显。MOPSO运行流程如图1所示,首先初始化种群中粒子的位置和速度，进而根据目标函数计算各个粒子的适应度值，由适应度值生成并更新非劣解集，将非劣解集存入外部档案库中，外部档案库采用拥挤距离的维护机制[9]，生成并更新个体最优粒子和全局最优粒子，在个体最优粒子和全局最优粒子的牵引下更新下一代粒子的速度和位置，迭代次数增加。若计算结果不满足迭代要求，则继续迭代优化。重复上述步骤，直至满足迭代要求为止，最终保存于外部档案库中的非劣解即为最终的优化结果。MOPSO中粒子速度和位置的更新公式如下：

(3)

Xk+1=Xk+Vk+1

(4)

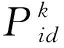
图1 多目标粒子群算法(MOPSO)流程图

惯性权重ω的取值关系到粒子群算法的个体搜索能力和全局搜索能力。较大的ω值有利于提高全局搜索能力，较小的ω值小有利于提高个体搜索能力，因此ω的取值对算法搜寻能力而言至关重要[19]。为了更好地平衡局部搜索能力和全局搜索能力，本文采用Clerc等[20]提出的粒子群改进算法，该算法采用收缩因子来确保MOPSO能够快速达到收敛状态。该改进算法的位置更新公式与标准多目标粒子群算法中位置更新公式相同，速度更新公式如下：

(5)

(6)

α=c1+c2

(7)

在上述改进的多目标粒子群算法中，通常取c1=c2=2.05，则α=4.1，常数乘子χ近似为0.729，且在该方法中，粒子的速度不必再设置上限[17]，方便算法使用。

2 算例分析

2.1 数值模型建立

本文基于某200 m级的高基座沥青混凝土心墙坝算例对基座体型和心墙厚度进行优化研究。该算例中坝高200 m，心墙形式为直心墙，高度为180 m，心墙厚度设置为优化变量，沥青混凝土心墙与混凝土基座间采用水平连接形式。心墙两侧为过渡料，过渡料与沥青混凝土心墙高度齐平。混凝土基座高30 m，基座底部长度30 m，基座上部宽10 m，基座其余尺寸设置为优化变量。计算模型如图2所示，模型中坝基范围沿坝体上下游方向取1倍坝高、沿竖直向取2倍坝高。坐标系以顺河向为x轴正向，以坝轴线指向左岸为y轴正向，以竖直向上为z轴正向。分析该大坝的某一坝段，坝轴向宽10 m。材料均采用摩尔-库仑模型，材料参数如表1所示。大坝筑坝过程分11步，第1步模拟生成地基；第2步模拟生成混凝土基座；第3步至第11步模拟坝体分层填筑至坝顶。

图2 计算模型示意图

表1 材料参数

2.2 土石坝基座体型及心墙厚度优化数学模型

(1) 确定优化参数及参数上下限。选取基座体型和心墙厚度共6个需要优化的尺寸作为优化变量，如表2所示。基座和心墙呈左右对称布置，优化变量示意图如图3所示。

表2 优化变量

(2) 选取优化目标，设置目标函数。本研究中以坝体最大竖直沉降Z、基座大主应力最大值S1、心墙大主应力最大值S2和坝坡抗滑安全系数F为优化目标，优化模型中目标函数设置如式(8)所示：

(8)

2.3 多目标优化分析

采用改进的多目标粒子群算法优化算例中的6个优化变量进行分析，该算法的粒子数目设为20个，迭代次数设为100代。算法搜寻结果如图4所示，并根据目标函数得出Pareto前沿。由图4可知，该算法搜索能力较强，所得的Pareto前沿集中，且各个目标函数间存在冲突关系，即一个目标函数的变优以另一个目标函数的变劣为代价，不能同时使所有目标函数同时达到最优值，决策者可根据实际需求在所得Pareto前沿中选取合适的优化方案。

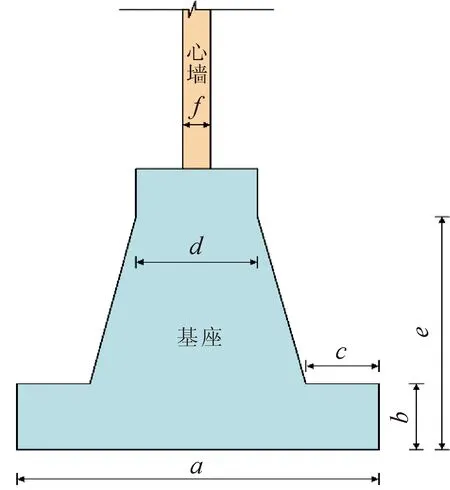
图3 优化变量示意图

图4 优化结果

由于Pareto前沿中有较多的优化方案，为使优化结果简洁明了，本文在Pareto前沿方案中有代表性地进行筛选，筛选条件为四个目标函数值均优于初始方案的目标函数值，在所有符合筛选条件的Pareto前沿方案中选取三个典型的筛选方案，初始方案和筛选方案的尺寸参数如表3所示，各方案的目标函数值如表4所示。

表3 初始方案及筛选方案的优化参数

表4 初始方案及筛选方案的目标函数值

由优化结果可知，三个筛选方案中坝体最大沉降分别较初始方案减少了0.08 cm、0.13 cm和0.14 cm，平均优化0.117 cm，平均优化幅度为0.08%，最大优化幅度为0.93%。在本优化问题中，坝体最大沉降优化程度较小，该优化目标敏感性较低，受到基座体型和心墙厚度影响小；三个筛选方案中基座大主应力最大值分别较初始方案减少了0.445 12 MPa、0.462 16 MPa和0.414 97 MPa，平均减少0.440 75 MPa，平均优化幅度为113.117%，最大优化幅度为118.61%，通过本文的优化方法，基座大主应力最大值受改善程度较大，将基座大主应力最大值由正值优化为负值，该优化目标的敏感性较高，受基座体型及心墙厚度的影响大；三个筛选方案中心墙大主应力最大值分别较初始方案减少了0.011 52 MPa、0.010 29 MPa和0.011 12 MPa，平均减少0.010 98 MPa，平均优化幅度为7.644%，最大优化幅度为8.02%，表明心墙大主应力最大值有一定程度的改善；三个筛选方案中边坡安全系数分别较初始方案增加了0.502、0.531和0.581，平均增加0.568，平均优化幅度为28.303%，最大优化幅度为29.48%，边坡安全系数改善程度较大，优化效果好，大坝边坡的安全性得到较大改善。

在沥青混凝土心墙坝多目标优化研究中，基座大主应力最大值受优化幅度最大，其次是边坡安全系数和心墙大主应力最大值，受优化幅度最小的是坝体最大沉降，表明基座大主应力最大值敏感性最大，在后续的优化分析中需要重点考虑基座体型和心墙厚度对该优化目标的影响，而坝体最大沉降受优化变量的影响较小，优化幅度基本可忽略，在后续优化分析中，可不将该参数纳入优化目标中，减少该参数对其他优化目标的影响，提高多目标优化的效率和精度。

3 结 论

(1) 相较传统的粒子群算法，本文使用改进的多目标粒子群算法，可针对多个目标函数进行多个优化变量的优化，使用外部档案库用于存储更新非劣解集，使用收缩因子提高算法的搜索能力和收敛速度。

(2) 优化结果与初始方案相比，优化效果明显，决策者可根据实际需求在Pareto解集选取合适的优化方案。三个筛选方案中，四个优化目标的优化程度由高到低依次为：混凝土基座大主应力、边坡安全系数、心墙大主应力和坝体最大沉降位移，平均优化程度依次为113.117%、28.303%、7.644%和0.08%，使用优化方法可达到对坝体体型多目标优化的效果。