砂土中螺旋锚理论扭矩相关系数工程适用性探讨
2022-09-06郝冬雪王金宇孔纲强
郝冬雪,王金宇,陈 榕,孔纲强,薛 楠
(1.东北电力大学建筑工程学院,吉林 吉林 132012;2.河海大学岩土力学与堤坝工程教育部重点实验室,江苏 南京 210098;3.河海大学土木与交通学院,江苏 南京 210098;4.浙江省送变电工程有限公司,浙江 杭州 310020)
螺旋锚或桩基础具有安装便捷,环境扰动小,噪声低及能够充分发挥深层土体抗力等优点而广泛应用于各类岩土工程问题中,尤其对于抗拔承载力需求较高的工程[1,2].目前,预测螺旋锚上拔承载力的方法有三种:圆柱剪切法,承载量法和安装扭矩方法,前两种为理论方法,后者为经验方法.安装扭矩经验法是根据安装过程中的实测扭矩,由经验关系推测螺旋锚或桩的承载力,即Qu=Kt·T,其中,Qu为极限承载力,Kt为扭矩相关系数,T为安装扭矩.这一公式被加拿大基础工程手册[3]所采用,在过去的20年中,已成功地应用于数千个锚的施工中.
扭矩在安装过程中沿深度不断变化,加拿大基础工程手册[3]建议利用整个埋深范围内的安装扭矩平均值,而Hoyt和Clemence[4]建议使用最后贯入深度3D范围内安装扭矩的平均值,并通过对91个多盘螺旋锚上拔力分析,建议对于杆径小于89 mm的方杆和圆杆螺旋锚,Kt=33 m-1;杆径等于89 mm时,Kt=23 m-1;杆径为219 mm时,Kt=9.8 m-1.对于小杆径锚,Zhang[5]同样认为可采用Kt=33 m-1来计算螺旋桩的上拔力.国际建筑规范等[6,7]建议杆径为73 mm时Kt=29.5 m-1.Hubbell集团[8]建议杆径为89 mm、114 mm时,Kt=23 m-1和20 m-1.加拿大基础工程手册[3]建议杆径接近200 mm时,Kt=9.8 m-1.上述规范或手册中的Kt建议值未考虑土质条件的影响,对于非常软、松或敏感性土体,Kt比规范中的建议值小[8].Livneh等[9]给出砂土中两个全尺寸螺旋锚的载荷试验数据,测量的Kt值为24.3 m-1和32.7 m-1,Sakr[10]报告了安装于油砂中杆径为178 mm螺旋桩的载荷试验,上拔时,Kt=10.3m-1~12.2 m-1,下压时Kt约为上拔时的双倍,取值为23.3m-1~23.9 m-1.值得注意的是,Kt值是在螺旋锚顺利安装的情况下获得的,即每旋转一周锚贯入土中深度为一个螺距.
尽管经验扭矩系数Kt的概念简单,但实际工程中诸多因素影响该值.扭矩测量方法、确定平均扭矩的深度、加载方向、锚桩垂直度、钻进速率、锚杆形状和尺寸、锚盘数量和尺寸、螺距、锚间距、安装和加载时间间隔、土壤性质等对Kt值均有影响[8,11,12],在理论上很难考虑各个影响因素.Tsuha等[11]给出砂土中深埋螺旋桩安装扭矩与承载力的理论关系,并进行离心机试验和界面直剪试验验证这个表达式.Giovanni等[13]分别利用加拿大和日本规范中的抗拔承载力公式,计算了不同上拔力设计值时不同密实度砂土中不同盘径与轴径条件下螺旋桩的安装深度,并利用Tsuha等[11]安装扭矩理论公式来评估螺旋桩的安装功率.
已有文献对螺旋锚安装扭矩的理论分析较少,Kt的取值基本是经验的,且多数适用于小直径螺旋锚;对于大直径螺旋锚,Kt如何取值的报道很有限.因此,本文基于Tsuha等[11]理论计算方法,计算砂土中不同几何尺寸及埋深时螺旋锚的扭矩相关系数Ktc,研究Ktc取值随土性参数、锚埋深、锚片直径等的变化规律,并与已有文献的经验建议值Kt进行对比,分析理论扭矩相关系数的工程适用性,可为大直径螺旋锚或桩利用安装扭矩估算上拔承载力提供参考.
1 扭矩相关系数理论计算
1.1 计算理论
螺旋锚上拔承载力为锚杆侧摩阻力与锚盘抗拔力之和[3,12],即
Qu=Qs+∑Qhi,
(1)
公式中:Qs为锚杆侧摩阻力,Qs=πdLqs;d为锚杆直径;L为锚杆与土体接触摩擦长度,取顶锚埋深H减去一倍盘径D;qs为锚杆侧壁摩阻力;qs=σ′vKstanδcv,σ′v为有效自重应力;Ks为侧向土压力系数,Ks=2(1-sinφ)[12];φ为土体内摩擦角;δcv为锚盘与土残余接触摩擦角.
Qhi为各锚盘抗拔力,Qhi=γ′HAhFq,其中Ah为锚盘投影面积,即锚盘面积减去锚杆截面积,γ′为土体有效重度,Fq为上拔承载力因数[14-16],本文分析采用了文献[8]建议的Fq,即取Meyerhof[16]深埋条件下的系数Nq的1/2,其建议的Fq比其他文献建议值低,以反映安装扰动对螺旋锚抗拔力的影响[17].
Tsuha和Aoki[11]利用扭矩平衡给出了安装扭矩的计算公式为
(2)

根据公式(1)和公式(2),可获得理论扭矩相关系数
(3)
1.2 砂土中不同几何尺寸螺旋锚的Ktc计算值
按照上述理论可以计算扭矩相关系数Ktc,为分析Ktc的影响因素,以单盘螺旋锚为例,变化基础几何尺寸及土性参数进行理论计算.根据文献[5],一般情况螺旋锚埋深比H/D>5可认为深埋,故下面选择深埋情况进行计算.保持d/D=0.25不变,选择盘径D=200 mm~600 mm,埋深比H/D=8、12、16,20,在内摩擦角φ为25°、30°、35°、40°、45°的砂土中进行计算,共计算了100个工况,获得的理论Ktc值如表1所示.其中,内摩擦角的变化范围可体现不同密实度的土质条件;螺盘材料和土质相对密度及摩擦角对δcv影响很小,对于平均粒径小于0.2 mm砂土,δcv可取29°[11].
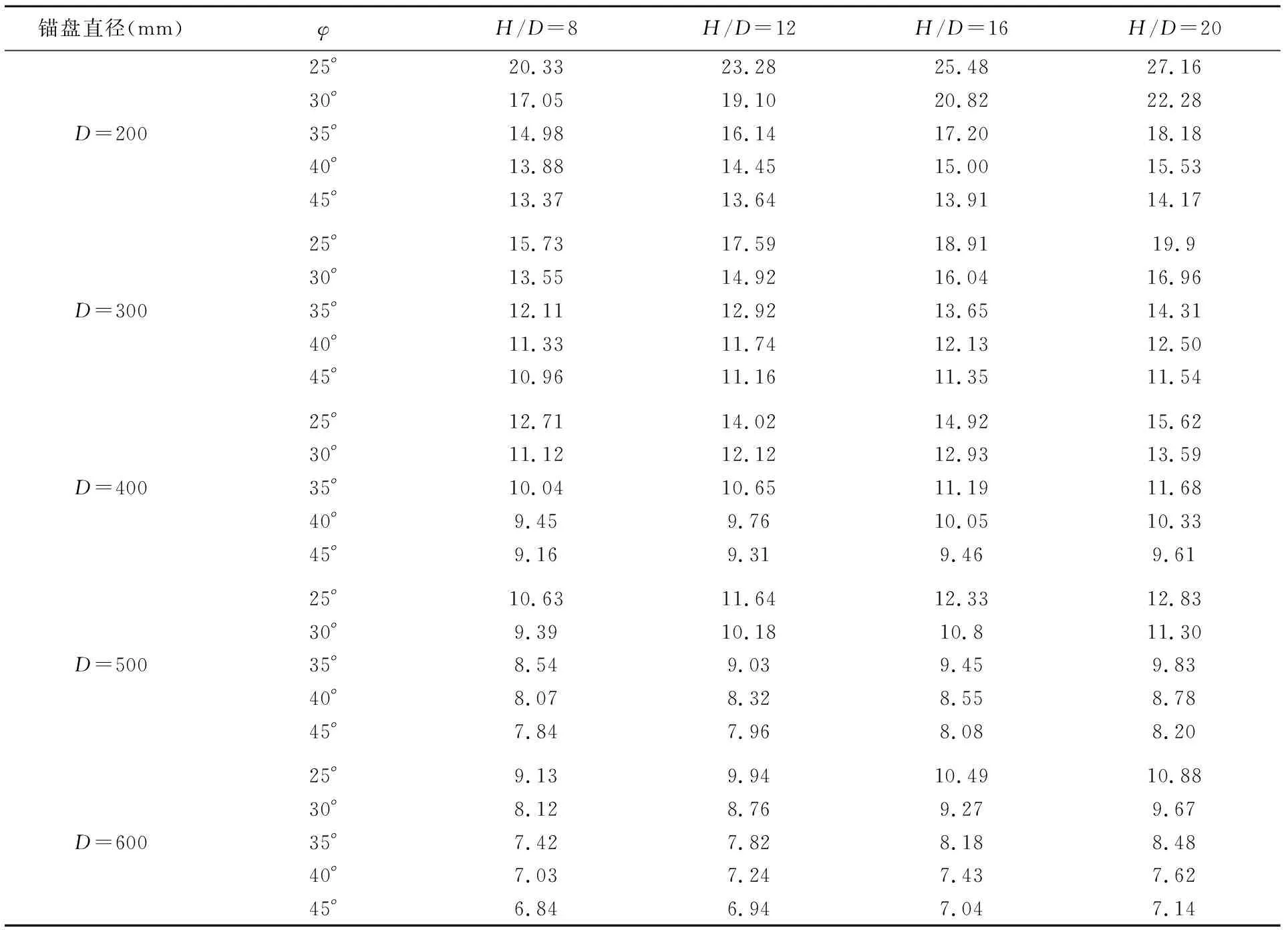
表1 不同几何尺寸砂土中螺旋锚的Ktc计算值
2 扭矩相关系数的影响因素分析
2.1 几何尺寸对Ktc的影响
φ=35°时不同埋深比下单盘螺旋锚理论扭矩相关系数与盘径关系曲线Ktc-D,如图1所示.由图1可见,相同埋深比时,随着盘径增加,扭矩相关系数Ktc随之减小,这与现场试验[3,10,11]获得的规律相同.对于φ=35°的情况,埋深比H/D在8~20之间变化时,D从200 mm增大到600 mm,Ktc降低了50.5%~53.3%.
当φ=35°时三种盘径尺寸下的扭矩相关系数与埋深比关系曲线Ktc-H/D,如图2所示.由图2可见,相同盘径时,Ktc随着埋深比H/D的增加而增大,且在大盘径时H/D对Ktc的影响减弱.D=200 mm时,H/D=20比H/D=6时的Kt值增加26.5%;而D=600 mm时,H/D=20则比H/D=6时Ktc值增加17.7%.相比于上述盘径的影响,埋深比对Ktc的影响较小.

图1 Ktc与D关系曲线(φ=35°,d/D=0.25) 图2 Ktc与H/D关系曲线(φ=35°,d/D=0.25)
2.2 内摩擦角对Ktc的影响
当D=200 mm不同埋深比时的扭矩相关系数和内摩擦角的关系曲线Ktc-φ,如图3所示.可以发现,当盘径及埋深比相同时,内摩擦角φ越大,扭矩相关系数Ktc减小,这与离心机和现场试验获得的规律相同[11],随着内摩擦角增加,Ktc减小速率放缓.埋深比越大,内摩擦角的影响越大,H/D=6时,φ为35°、40°和45°时的Ktc值较φ=30°时分别减低了9.6%、14.4%和16.6%;而H/D=20时,φ为35°、40°和45°时的Ktc值较φ=30°时分别减低了18.4%、30.2%和36.4%.
当H/D=12五种盘径时的扭矩相关系数和内摩擦角的关系曲线Ktc-φ,如图4所示.由图4可见,盘径越大,内摩擦角对Ktc的影响越小,即较大盘径时,随着内摩擦角增加,Ktc减小速率放缓.D=200 mm时,φ为35°、40°和45°时的Ktc值较φ=30°时分别减低了15.5%、24.3%和28.6%;D=600 mm时,φ为35°、40°和45°时的Ktc值较φ=30°时分别减低了10.7%、17.3%和20.7%.

图3 不同埋深比时Ktc-φ关系曲线(D=200 mm)图4 不同盘径时Ktc-φ关系曲线(H/D=12)
3 Ktc预测上拔承载力的工程适用性
3.1 扭矩相关系数实测值及与理论值对比分析
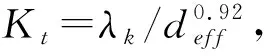
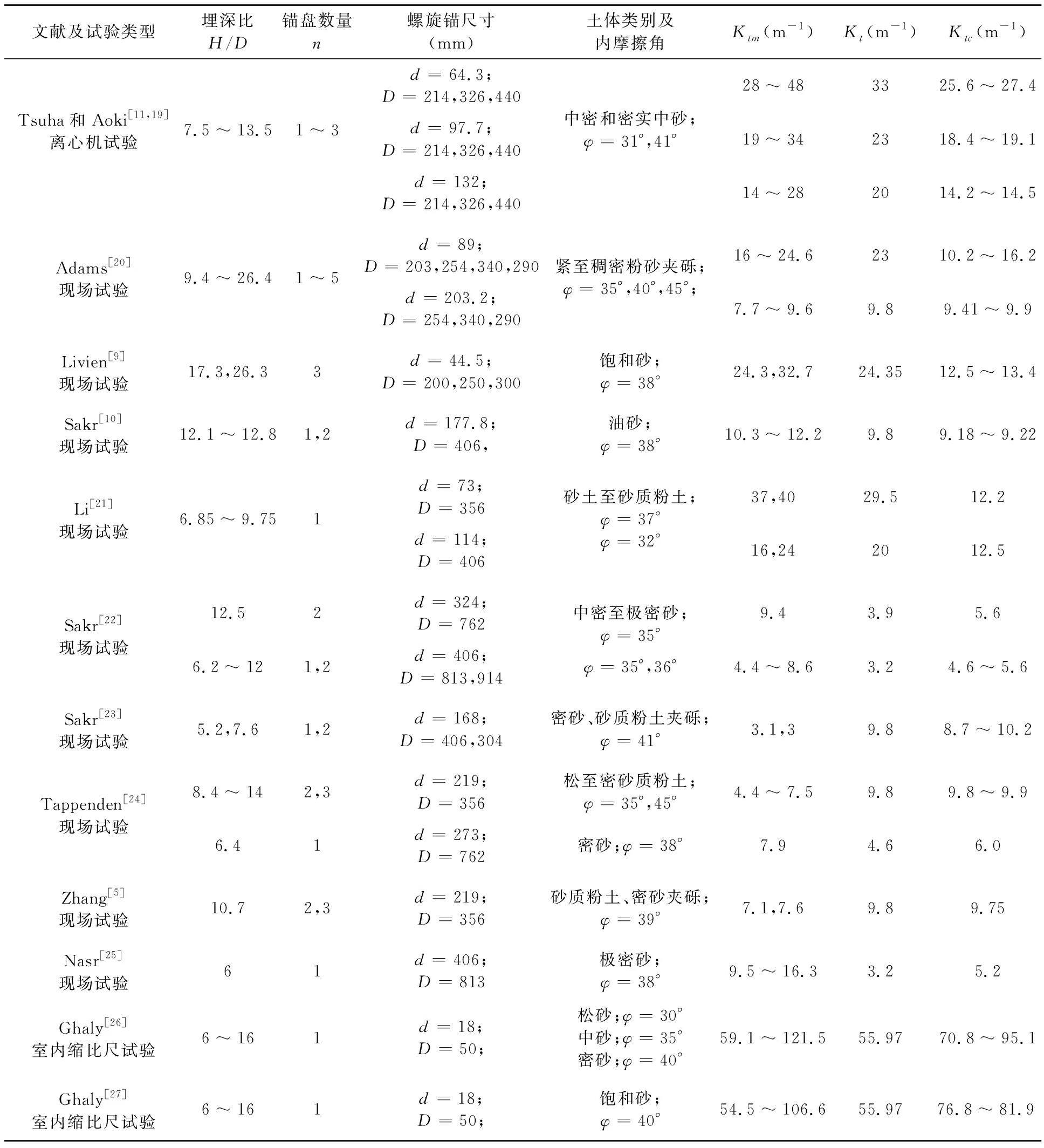
表2 已有文献试验扭矩相关系数
表2中105例试验数据的扭矩相关系数理论值Ktc与实测值Ktm,如图5所示.其中,方块点为离心机试验数据,圆圈为现场试验数据,三角形为室内缩比尺试验数据;实心代表理论计算值Ktc,空心代表实测值Ktm.由图可见,相同埋深比时,室内缩比尺模型试验的Ktm值明显高于现场及离心机试验,这与螺旋盘径D有关,D值越小,Kt值越大;由于理论Ktc值能够反映D的影响,因此,相应地,相同的试验方法时,Ktm值与Ktc值比较接近.为更清楚地分析理论扭矩相关系数Ktc的准确度,将不同试验方法的理论与实测扭矩相关系数之比Ktc/Ktm,如图6所示.离心机试验共18个数据点,D=214 mm~440 mm,d/D=0.3,H/D=7.5~13.5,其中δcv采用原文献提供的值19.8°,Ktc/Ktm的范围0.51~1.01;现场试验共42个数据点,除三个异常高估的试验点外,其它Ktc/Ktm的范围为0.41~1.37;室内缩比尺模型试验共45个数据点,Ktc/Ktm的范围为0.72~1.49.整体上,105例试验数据绝大多数Ktc/Ktm值在0.5~1.5之间,仅有三个高于1.5和六个低于0.5的数据点,这九个点为现场试验数据,主要是因为现场地质条件复杂,为成层土或非均质土、有地下水等,用于计算Ktm的T值为平均值,而理论Ktc值是基于均匀土体的计算结果.由上述对比分析可见,对于不同试验条件、不同几何尺寸螺旋桩或锚,理论计算的扭矩相关系数Ktc与实测结果Ktm较为一致.

图5 不同试验条件下的扭矩相关系数Kt图6 理论与实测扭矩相关系数之比Ktc/Ktm
3.2 Ktc预测上拔承载力的工程适用性
工程中预测螺旋桩或锚上拔承载力的方法有理论公式和安装扭矩经验法,理论方法根据可能发生的破坏模式(柱状或独立破坏模式)选择不同的计算公式,一般工程中认为盘间距比S/D=3即达到了独立破坏模式,可采用公式(1)计算;经验方法根据经验获得的Kt值乘以安装扭矩来估算上拔承载力,关于Kt的经验取值上文已描述,工程中仅提供不同杆径时的Kt值,对其它因素的影响未体现.因此,本文提出采用理论扭矩相关系数Ktc来预测上拔承载力,下面对表2中105例试验条件下的上拔承载力预测来讨论其工程适用性.
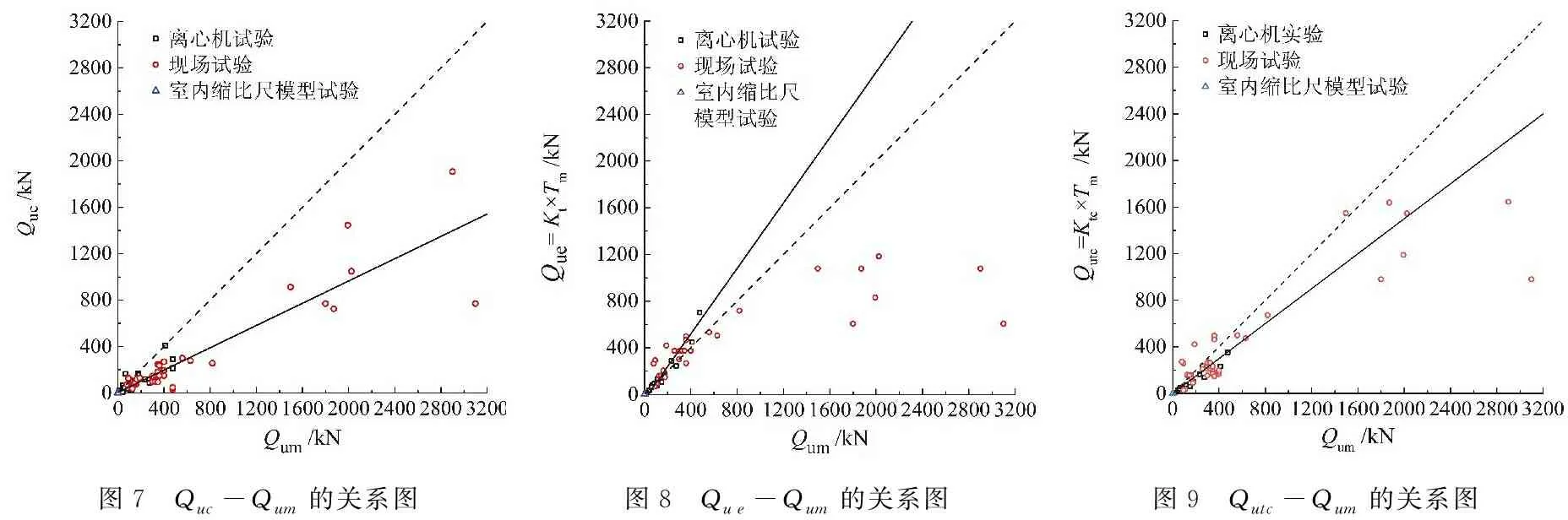
图7 Quc-Qum的关系图图8 Que-Qum的关系图 图9 Qutc-Qum的关系图
由理论公式(1)计算的螺旋桩或锚的上拔承载力Quc、经验Kt值估算的上拔承载力Que及本文所建议采用理论Ktc来估算的上拔承载力Qutc与实测值Qum的关系,虚线为斜率等于1的直线,实线为各方法预测的Qu与Qum关系的线性拟合,如图7~图9所示.现场试验点较离散,这可能是由于现场土质条件复杂,或者安装扭矩测量的误差引起的.图7、图8和图9中拟合直线的斜率分别为0.48、1.42和0.75,相关指数R2分别为0.84、0.95和0.93.由此可见,基于理论相关扭矩系数Ktc估算的上拔承载力与实测值吻合效果最好,由理论公式直接计算和理论相关扭矩系数计算的结果整体上较实测值分别低估52%和25%,而根据经验扭矩相关系数的计算结果则高估42%.通过上面对比分析,无论从安全性还是从准确性的角度,由Ktc估算Qu的方法效果最好,因此,建议工程中采用这种理论扭矩安装系数与实测安装扭矩相结合的方式来估算螺旋桩或锚的极限上拔承载力.
4 结 论
基于已有安装扭矩的理论计算公式,提出采用理论扭矩相关系数来预测螺旋锚极限上拔承载力.通过变化螺旋锚几何尺寸和土性参数分析其对扭矩相关系数的影响规律;利用搜集整理的相关试验数据,对比预测上拔承载力各方法的准确性,探讨本文所提方法的工程适用性,主要结论如下:
(1)盘径、埋深和内摩擦角对扭矩安装系数Ktc均有影响,其中盘径的影响最大.Ktc随着盘径增加明显减少,随埋深比H/D的增加而增大,且在大盘径时H/D对Ktc的影响减弱.随着内摩擦角φ增加,Ktc减小,且减小速率逐渐放缓.埋深比越大,内摩擦角的影响越大,盘径越大,内摩擦角对Ktc的影响越小.
(2)105例已有文献试验数据对比结果表明,对于不同工程地质条件、不同几何尺寸螺旋桩或锚,理论计算的扭矩相关系数Ktc与实测结果Ktm较为一致,绝大多数试验点的Ktc/Ktm值在0.5~1.5之间.
(3)通过极限上拔承载力理论公式直接计算、扭矩相关系数经验法和基于理论相关扭矩系数Ktc估算的上拔承载力与实测值进行对比,结果表明,利用Ktc的估算结果效果最好,因此,本文建议工程中采用这种理论扭矩安装系数与实测安装扭矩相结合的方式估算极限上拔承载力.
(4)值得注意的是,本文所用的安装扭矩的理论计算公式未考虑锚片厚度、顶部压力、钻进不连续等复杂情况,因此,对于较特殊的安装情况,应进行专门研究.
