基于伴随方程复杂管网泄漏反向寻源的数值模拟研究

韩宇波，常 畅，宋 琪，洪文鹏

(1.珠海横琴能源发展有限公司，广东 珠海 519015；2.东北电力大学能源与动力工程学院，吉林 吉林 132012)

目前大多比较先进成熟的泄漏检测定位方法和技术均是针对单一的长直管道，例如长输油、输天然气管道[1-3].然而，对于拓扑结构复杂的多分支型管网来说，例如供热管网、供水管网，这些方法将不能直接被利用.复杂供水管网广泛存在破损、泄漏等问题.给社会生产和人民生活造成巨大经济损失以及诸多不便，因此，为了及时的发现，定位，并修补泄漏，消除水泄漏造成的潜在危险，本文针对供水管网泄漏检测定位，提出了基于伴随方程的反向寻源方法.

1994年，靳世久[4]提出基于负压波的管道泄漏检测定位方法.1996年，杨开林、郭宗周[5]提出了基于恒定流动模拟的静态泄漏检测法和基于水力瞬态模拟的瞬态泄漏检测法.2001年，Verde和Mpesha[6-7]分别提出了最小非线性观测器和频率响应法来确定泄漏点的位置.2002年，Costa[8]运用参数估计法来对管网进行泄漏检测和泄漏点定位.2003年，Ferrante[9]提出了基于小波的分析方法，根据上、下游传感器的时间差进行泄漏点定位.2007年，刘畅等[10]利用多元统计学上的聚类分析方法，对管网故障模拟的数据进行聚类分析，并利用多元统计学上的判别分析方法，对泄漏情况进行故障定位.2010年，杨红英等[11]研究了基于Duffing振子的管道泄漏检测方法.2014年，吕玉坤等[12]对于单点泄漏的枝状供热管网，引入插入虚拟节点的方法，来判断管网是否泄漏与泄漏可能发生的位置.2015年，Wachla等[13]采用人工神经模糊模型对供水管道泄漏进行定位.2015年，燕山大学黄满义等[14]针对单一参数研究输油管道泄漏，引入混沌特性分析及递归图方法对管道泄漏检测与定位方法进行分析.2016年，刘炜，刘宏昭[15]从时间序列角度出发，提出一种基于模糊集理论的输油管道泄漏检测定位方法.

Enting[16]将反问题用于大气污染物扩散研究.Bagtzoglou[17]将反演方法用于地下水污染定位研究.郭少东等[18]采用计算流体力学的方法求解伴随方程和MCMC方法的室内污染源反演结果的研究.Zhang[19]将源项反演方法用在室内污染源定位研究.

Liu和Zhai[20-22]使用伴随方法实现了室内污染源的快速辨识，但他们并没有将其作为最优化方法使用，而是利用伴随方法的特性，将在流场固定的基础上实现了时间和对流项的取反，以反向方法的方式实现了污染源的辨识.

总结以上国内外研究现状发现，现有的管网漏损检测定位方法并不能满足日常管网漏损检测的需求，在精度或者经济性上均存在一定的缺点.目前，基于流场求解的反向寻源技术能够实现准确地检测和定位，在诊断空气污染和水污染源头的方向上取得了较好的效果，因此，本文将基于伴随方程的反向寻源技术应用于供水管网中，以更快的实现复杂管网的泄漏检测和定位.

1 数学模型的建立

1.1 单相流瞬态伴随方程的推导

建立管网流场瞬态方程，找出与流场瞬态压力耦合的参数，保留这些参数，对流场瞬态方程进行简化.

不考虑摩擦、阻尼等因素的影响，一维半无限区间下压力瞬态流动方程为

(1)

初始条件为

当t=0时，p(x，t)=0，v(x，t)=0；

边界条件为

当x=0时，p(x，t)=p0(t)，v(x，t)=0；当x→+∞时，p(x，t)=0；

公式中：p为压力，Pa；v为液体流速，m3/s；a为压力波速，m/s；ρ为液体密度，kg/m3.

(1)以管网泄漏对流场形成的压力波影响为依据，选取适当敏感度函数.所选取的压力波敏感函数

h(α，p)=p(x，t)δ(x-x*)δ(t-t*)，

(2)

公式中：p(x，t)为压力波传播函数；α为狄克拉函数，α与α为泄漏或堵塞故障发生的位置与时间；α为敏感度参数(过程变量)；p为压力.

(2)将敏感度函数对压强求导，并引入伴随算子，推导管网流场瞬态伴随方程.利用高斯散度定理处理，设置边界条件，得到流场瞬态伴随方程.

量化系统状态量的度量目标函数

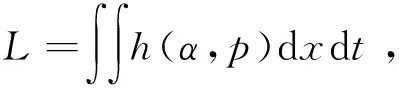
(3)

公式中：h(α，p)为系统状态函数；α为系统矢量参数(例如[v，D，a]；p为压力，积分区间是给定的空间-时间区间，系统关于矢量参数αk的临界灵敏度可以通过对参数αk求微分得到

(4)

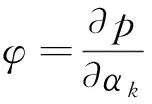
(5)

初始条件为

当t=0时，Φ(x，t)=0；当t=0时，λ(x，t)=0；

边界条件为

当x→+∞时，φ(x，t)=0；

当x=0时，λ(x，t)=0，φ(x，t)=0；当x→+∞时，λ(x，t)=0.

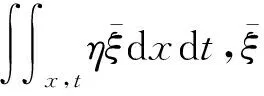
(6)

初始条件为

φ*(x，T)=0，λ*(x，T)=0；

边界条件为

φ*(0，t)=p0(t)，λ*(0，t)=0.

这样伴随方程(6)中未定义函数仅剩余h(α，p)项，它的形式还需要根据所要研究的具体工况条件确定，将方程(2)中选取的适当函数两边取偏导可得

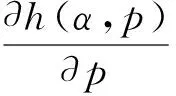
(7)

将方程(7)带入到伴随方程(6)中，经过整理得

(8)

初始条件为

φ*(x，T)=0，λ*(x，T)=0；

边界条件为

φ*(0，t)=p0(t)，λ*(0，t)=0.

考虑流动过程中摩擦阻力，最终得出管网流场瞬态伴随方程

(9)

边界条件为

φ*(0，t)=p0(t)，φ*(L，t)=0，λ*(0，t)=0，λ*(L，t)=0；

初始条件为

φ*(x，T)=0，λ*(x，T)=0.

公式中：t为时间变量；x为距离变量；L为距离常数；T为时间常数.

(3)将伴随方程进行空间与时间的反向处理，应用拉普拉斯变换和傅里叶变换求解析解，得到反向寻源模型.

做反向处理，τ=td-t，x为-x，可得反向伴随方程

(10)

公式中：τ=td-t，td为检测的时间；xd为检测的位置.

1.2 模型验证

传统的正向求解方法是通过对每个可能的泄漏位置进行正向求解，判断泄漏点的位置，但是这种方法因为需要多次求解从而变的低效.因此，本文利用伴随理论和数学方法结合流体力学中的单相流体控制方程推导伴随方程，建立逆向模型，如图1所示.

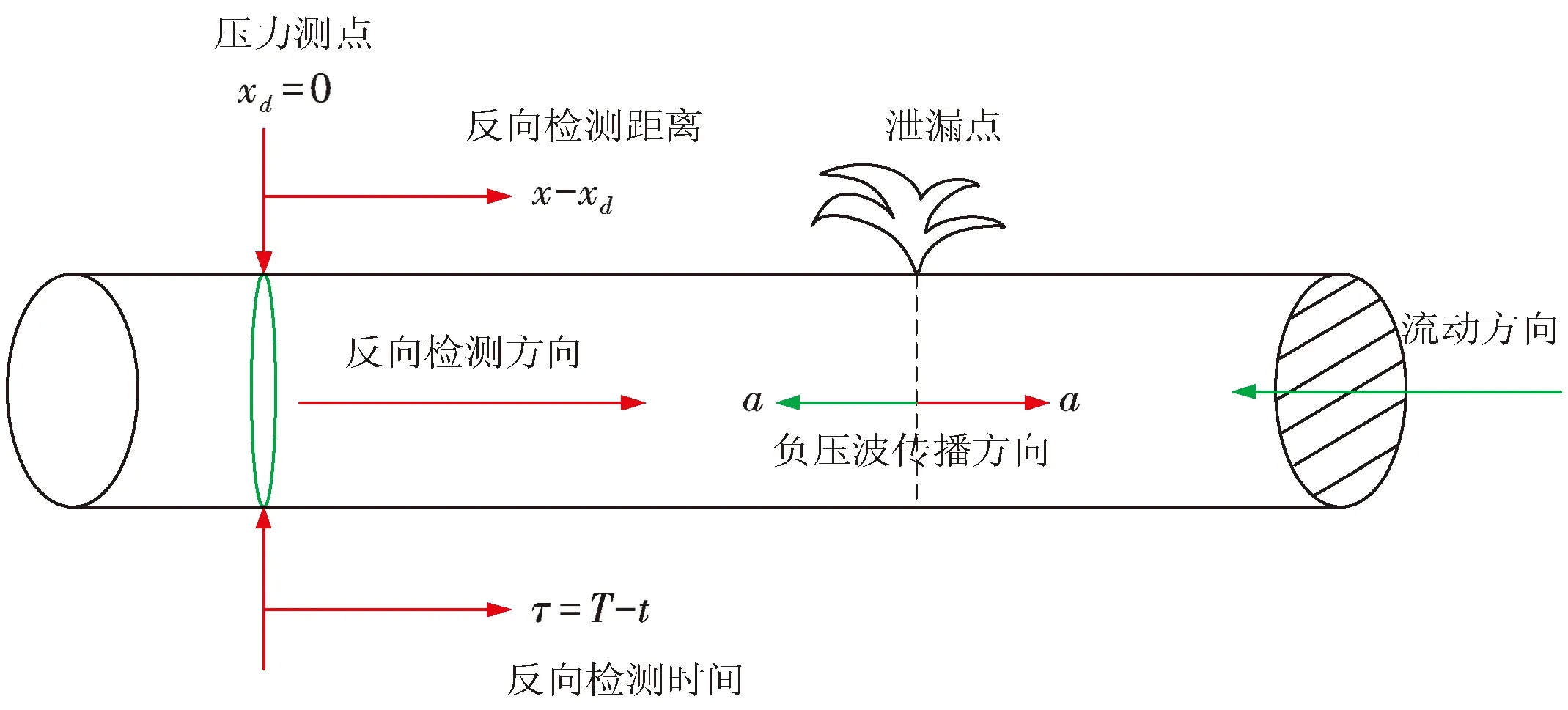
图1 泄漏位置检测原理图

从检测点开始传播的压力变化曲线，如图2所示.从图2中可以看到明显的突升变化过程，该曲线是通过在假定的压力测定点出检测到负压波信号，并设置为xd=0，即为原点，得到反向传播时间，τ=5 000 m/1 300 m/s，且泄漏点出的压力变化为突升25 kPa.

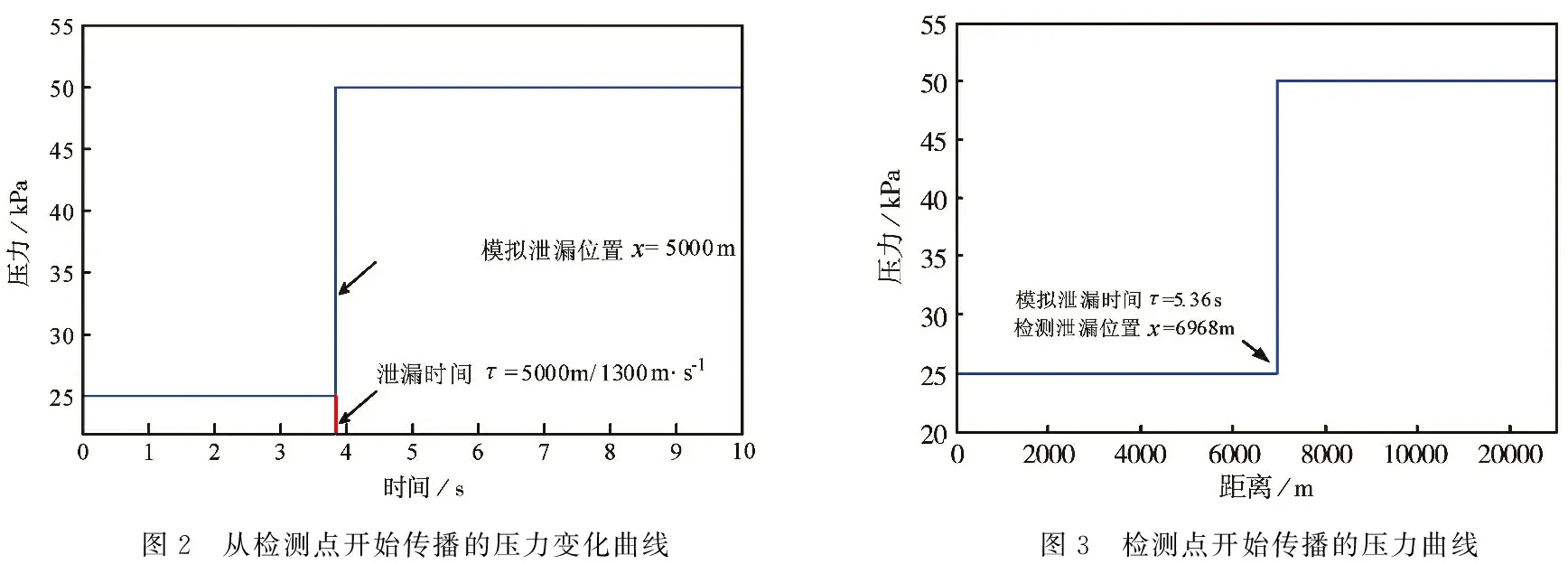
图2 从检测点开始传播的压力变化曲线图3 检测点开始传播的压力曲线

假设在xd=0监测点处开始检测压力波，如图3所示，模拟了泄漏时间τ=5.36 s时，压力波反向传播变化曲线，压力值从25 kPa突变到50 kPa，泄漏突变的位置在x=6 968 m处.

综上所述，基于压力输运控制方程，应用伴随理论及一些数学方法推导出相应的管网瞬态伴随方程，通过MATLAB模拟了检测点处逆向压力波变化规律，明确了由压力输运方程推导出来反向伴随方程可以应用于管道泄漏检测与定位.

2 实验结构及数值模拟计算

2.1 实验结构

以实验为基准验证使用Open FOAM进行数值模拟的结果，实验中对管道泄漏前后以及泄漏瞬间的压力进行了测量.实验系统图如图4所示，主要由一个实验段，五个压力变送器，两个电磁流量计，两个过滤器，一个水箱，一个水泵，一个数据采集仪和一个电脑组成，整体分为复杂管网微缩实验系统、信号传输系统和数据处理系统三个基础部分.

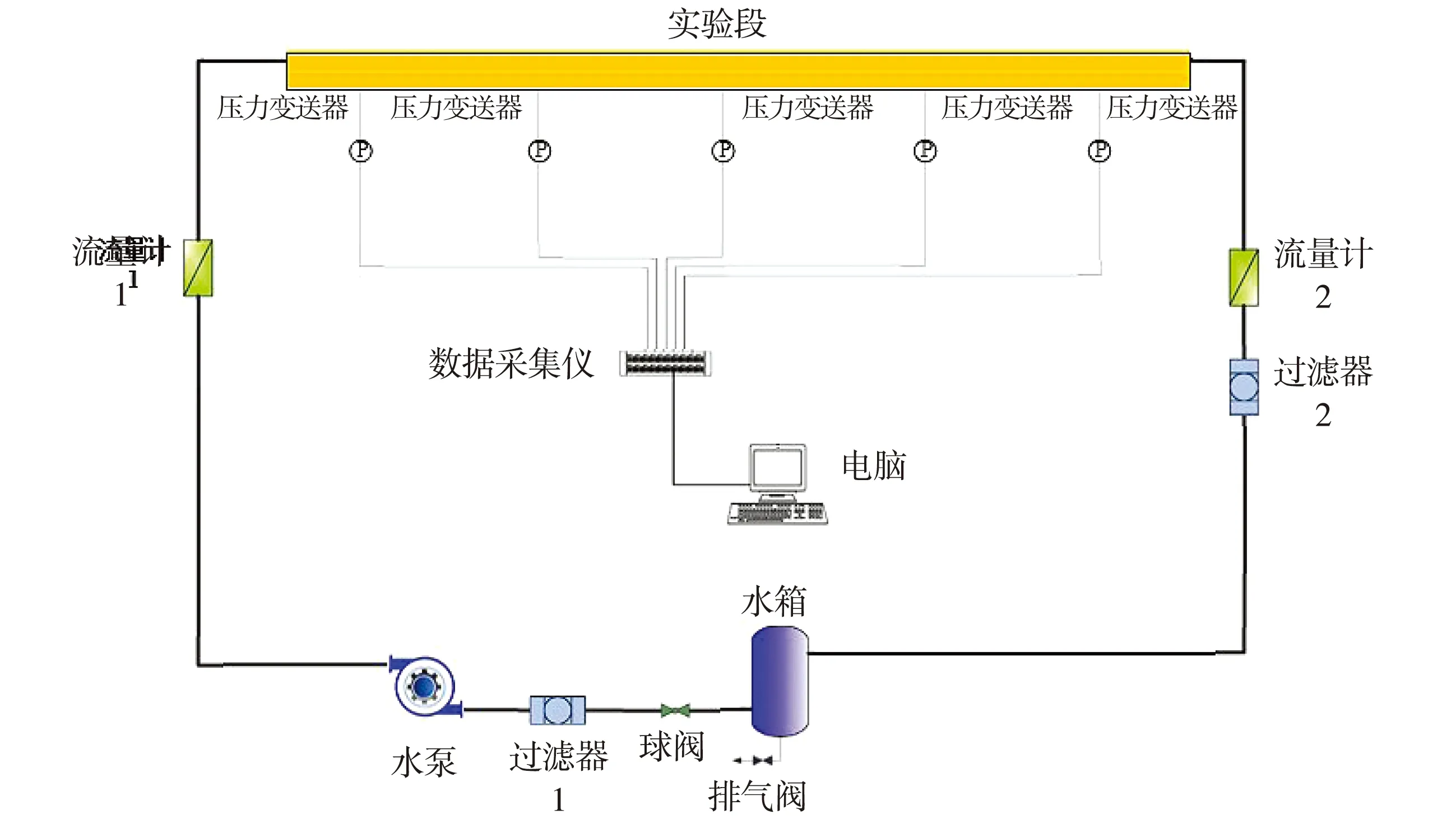
图4 实验系统图

由于实际供水管网雷诺数大致范围在5×104到4×105之间，且管网稳定运行时管内流态为阻力平方区，结合模拟供水管网、运行参数及实验室空间，根据相似理论进行了管网模型设计.选择水为管网运行介质，为了满足可视性，使用强度大、安全性高、安装简单等要求，选择有机玻璃为管网主体管道，U-PVC为阀门和四通材料.

管网主体为4×4复杂环状管网，如图5所示.管材为内径12 mm外径20 mm的有机玻璃，泄漏内径4 mm，外径6 mm.管网各环管段尺寸相同，长均为0.85 m，宽均为0.38 m，管段中共有25个节点，其中5个节点为压力测点.共设置20个泄漏点，其中10个位于管段节点，另外10个为管段中点，分别对节点和管段中泄漏进行研究.

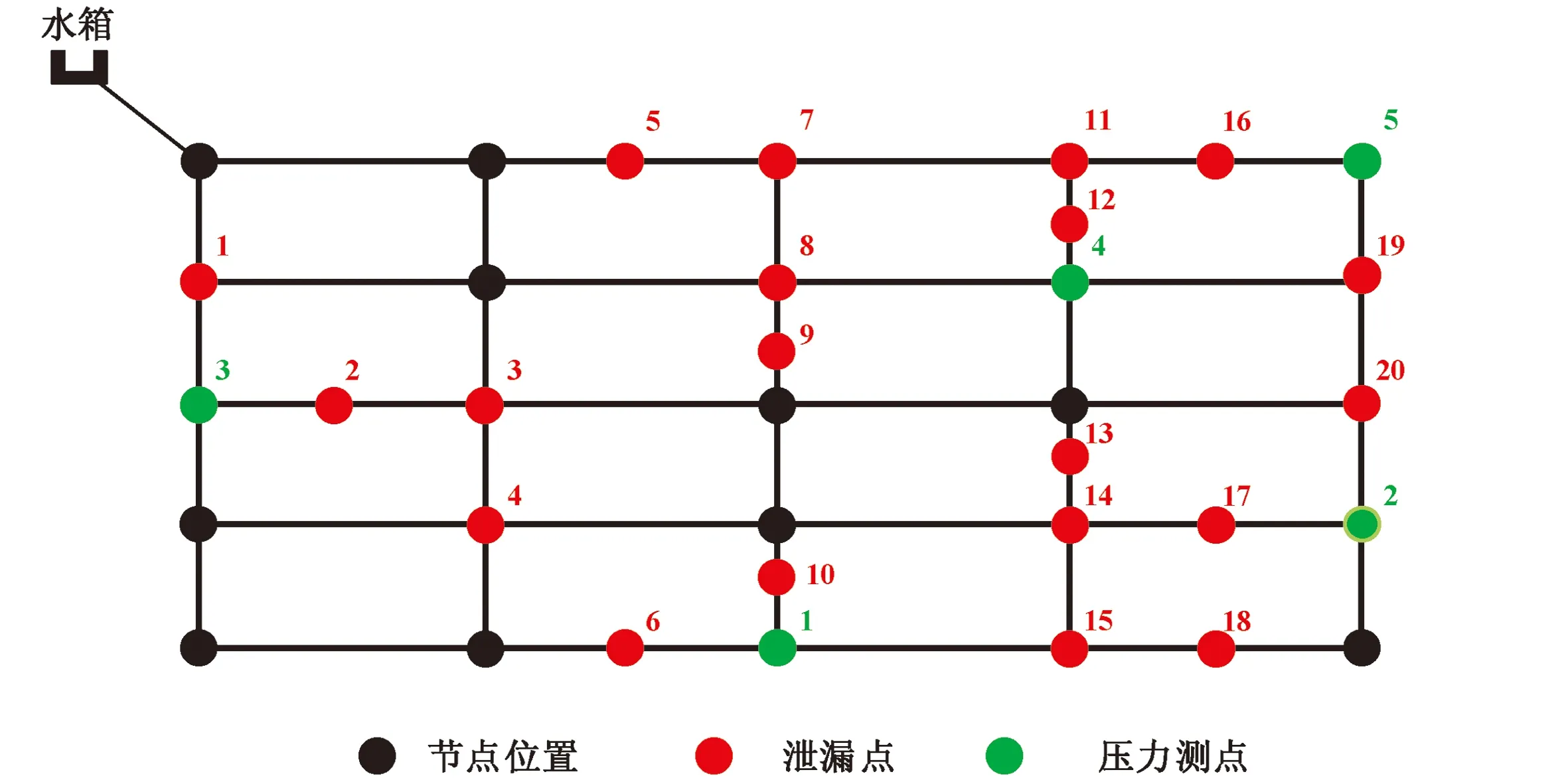
图5 实验台压力测点和泄漏点的分布

2.2 数值模拟计算

2.2.1 网格的划分

根据实验段尺寸，建立模拟模型，忽略壁厚，管道直径12 mm，泄漏孔直径4 mm，整体采用三维六面体结构化网格，管道交叉处的与泄漏口处分别采用Y-Block和O-block，实验段为4×4管网，网格数达9 061 188，为了便于计算，将其简化为2×2管网，网格数减少到4 420 092，计算效率大大提高.

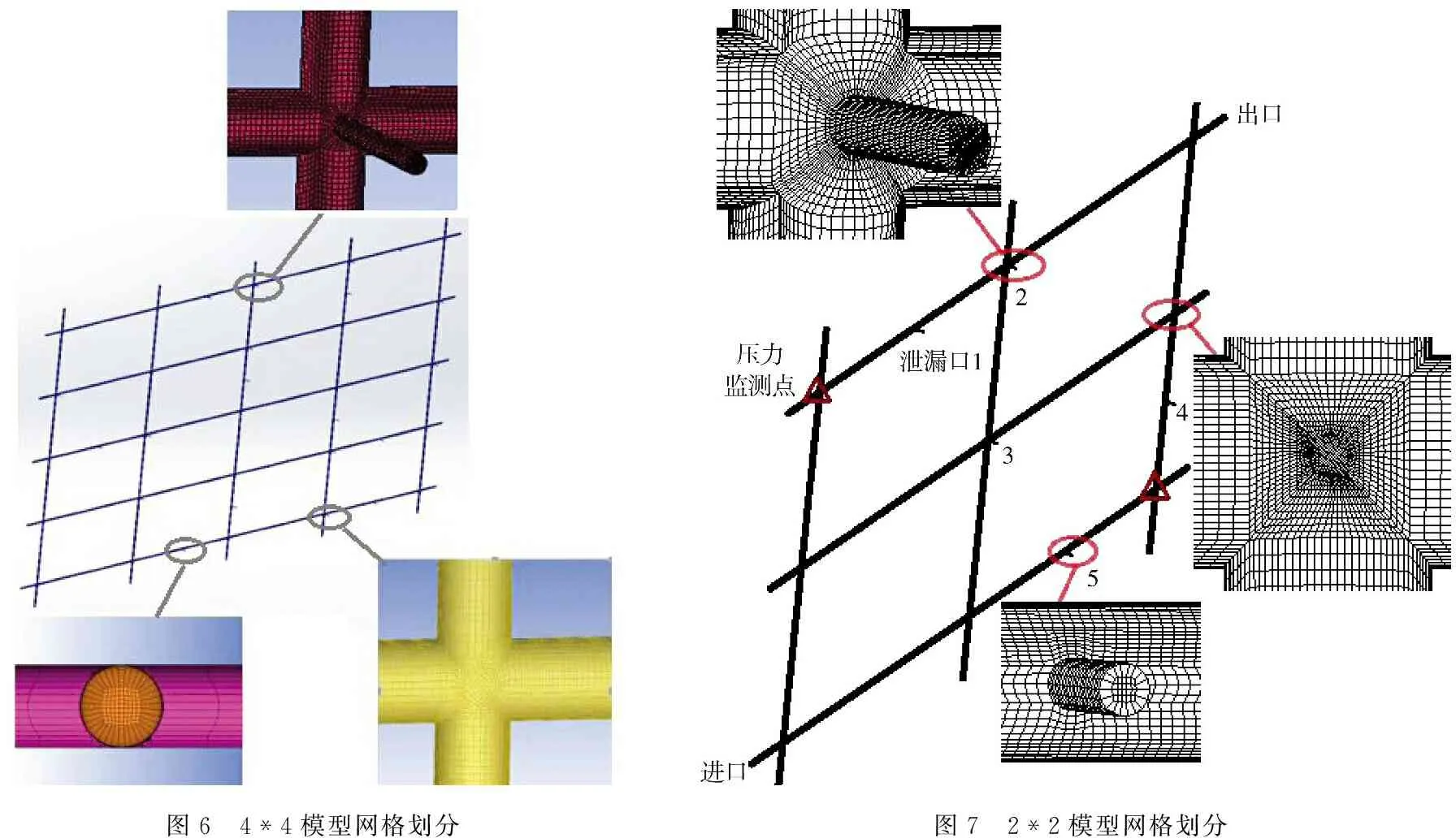
图6 4*4模型网格划分图7 2*2模型网格划分

本文选择三维六面体结构化网格，如表1所示.表1做了网格无关性验证，本次模拟采用的网格数为4 420 092.

表1 网格无关性验证

由表1可知，以泄漏点1为例，当网格数达到400万，监测点压力的压降几乎不变，为了提高管网泄漏模拟计算的精度和效率，对管道相贯处，相贯处的泄漏点，以及管道进出口等进行了网格加密处理.

2.2.2 复杂管网泄漏检测及相关性分析

同一泄漏源产生的压力波，其传播到不同传感器所需的时间不同，因此不同传感器上所接收到的信号记录也不会相同，但是当把两个传感器记录其中之一给予一定的时移后，会发现此时两个信号序列之间具有很大的相似性.根据压力波传到两个监测点的时间差，压力波波速即可确定泄漏点的位置.

为提高时延估计的精度，采用了希尔伯特变换和二次相关法相结合的新时延估计方法，其基本思路在于结合两种分析方法，将其与相关函数的绝对值相减，相关峰值点被保留，其附近的点的相关值相应的减小，主峰值点被锐化，精度大大提高，在如上所述的二次相关法的基础上，加入了希尔伯特变换，并结合了二次相关方法，原理如图8所示.

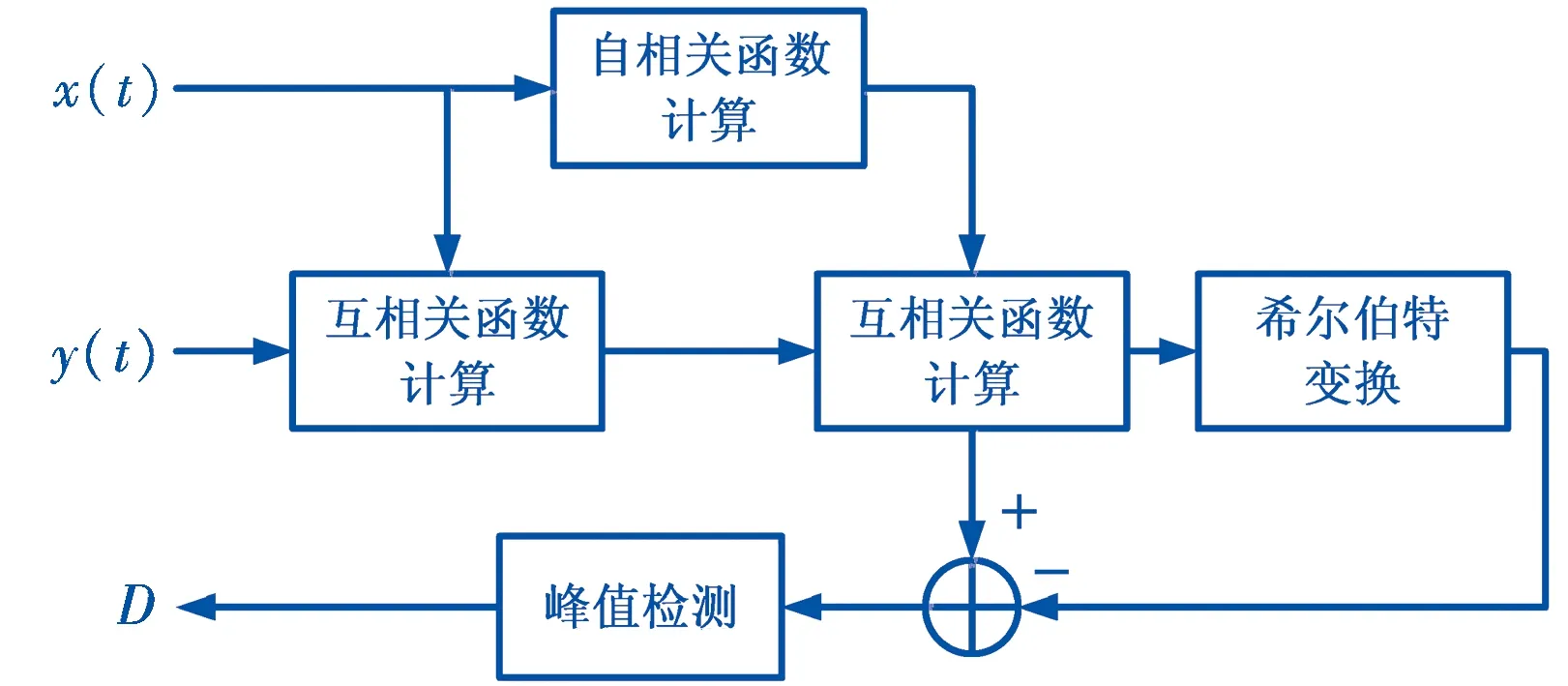
图8 新时延估计法原理图

锐化了主峰值点后，利用互相关系数法判断信号相似程度，其原理是两列信号的相关系数在泄漏前通常在零值附近，出现泄漏后，信号的相关系数在零附近有所偏移，信号峰值点所对应的时间就是相关系数最大时所对应的时间点.假定两列不同随机信号s1(t)、s2(t)，互相关函数为

(11)

公式中：RS1S2(τ)可以计算出s1(t)和s2(t)信号的相似程度，它是信号的相关函数，其中，τ为时移.

以泄漏孔1、泄漏孔2、泄漏孔3为例，压力波的传播速度1 483.2 m/s，设置时间步长为5e-7s，采用PISO算法，自定义求解器，管网内流体流动稳定到2 s，出现泄漏.

简化4×4管网之后的管网系统图，如图9所示.设置两个压力测点，测点1(左上方测点)和测点2(右下方测点)，监测泄漏前后的压力波信号.模拟泄漏前和整个过程测点1和测点2通过新时延估计法和互相关分析法处理后得到的信号相关性图，如图10～图12所示.相关系数的最大值在泄漏前通常在零值附近，出现泄漏后，信号相关系数的最大值在零附近有所偏移，通过相关性对比图可知，管道泄漏的出现，最大相关系数的值下降，我们通过对比管道泄漏前后的阈值，判断管道是否出现了泄漏.

图9 管网布置示意图

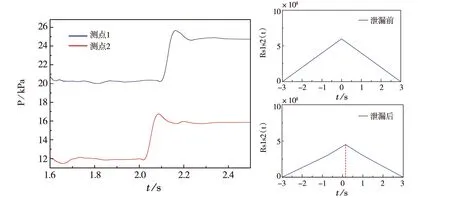
图10 不同测点，1点泄漏前后压力及相关性对比图

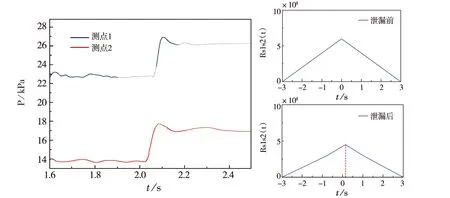
图11 不同测点，2点泄漏前后压力及相关性对比图

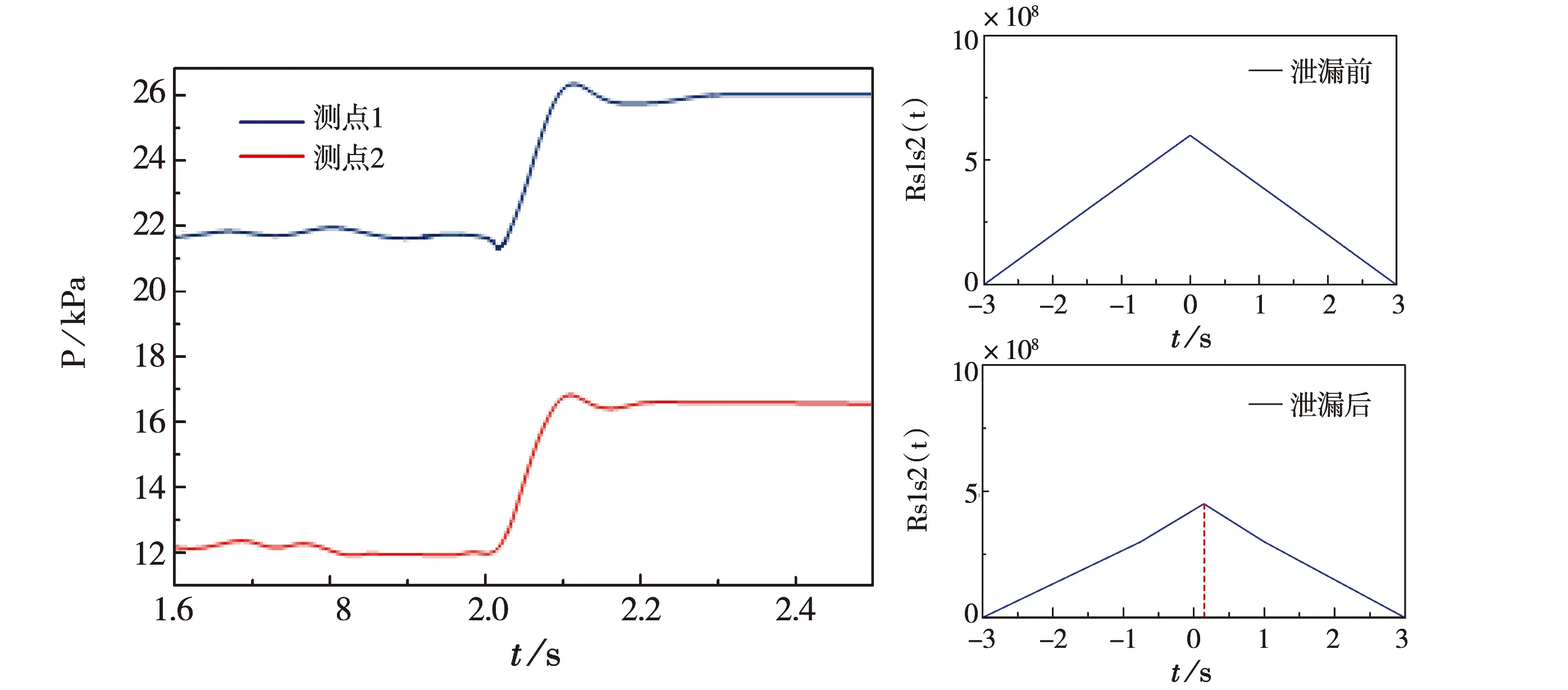
图12 不同测点，3点泄漏前后压力及相关性对比图

从上图10至图12中可知，管网出现泄漏后，压力瞬间增大，与实际实验数据相反，这是由于模拟过程添加了逆向伴随模型，大大加快了计算效率.管网流动稳定后，2 s时出现泄漏，压力波迅速向管道上下游进行传播，在泄漏后的0.2 s内压力变化明显，出现上升的趋势，管道内部的沿程压力也升高，略微波动后稳定于略微高于管道正常压力的值.管道入口我们采用速度进口，入口速度一定即流量一定，泄漏后短时间内，泄漏点上游的流速下降后又恢复到了泄漏前的稳定值，左上方测点距离泄漏孔较近，右下方测点较远，其接收到压力波信号时间大于左上方测点，压力值大于左上方测点，总体趋势相同，压力变化范围在10 kPa～28 kPa之间，泄漏后相关系数减小，最大相关系数对应的时间有延迟，符合相关性验证.

管道内流体流动2 s稳定后，1，2两点同时发生泄漏的模拟图，相对于一点泄漏，两点泄漏的峰值差更小，压力变化范围也较小，但总体趋势一致，符合逆向模型得出的结果，可以利用上述方法对管网实现在线监测，如图13所示.

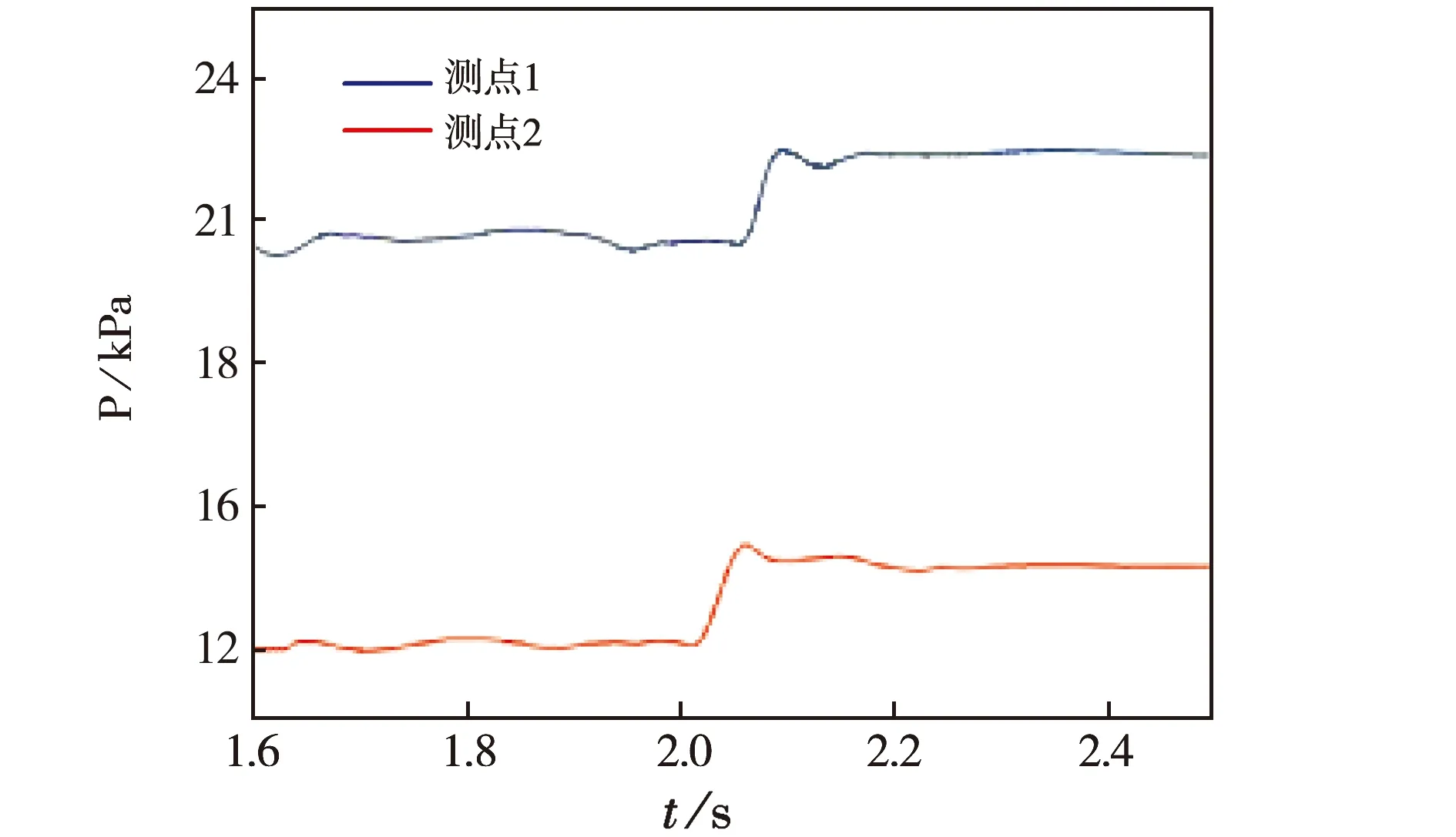
图13 不同测点，1，2两点同时泄漏前后压力对比图

综上所述，管道突然出现泄漏后，相比于泄漏前，管道首末两端的压力差更大，压降作用也更明显.加入了反向模型的管网，泄漏后管网各个监测点的压力迅速上升后略有降低，之后维持在一个较高的值，比较不同泄漏位置的压力值，泄漏位置靠近管道进口，下游压力降低幅度越高，越靠近管道出口，上游压力下降幅度越小，根据管道沿程各监测点收集到的压力值梯度，可知泄漏情况的发生.

2.2.3 复杂管网泄漏位置的确定

管网泄漏检测及定位流程图，如图14所示.当管网出现泄漏时，我们首先通过上述方法进行泄漏检测，确定可能发生泄漏的位置，判断各部分泄漏量的多少，然后利用全局搜索方式，最终确定泄漏点.

结合模拟结果，我们分析了两列信号s1(t)和s2(t)的相关性(以1点泄漏采集为例)，计算可知压力波传到两个监测点的时间差为△t=1.15×10-3s，根据已知的压力波波速信息就能计算出泄漏孔距离两个测点的距离，两者距离差约五倍，由于管网线是同程的，可知可能出现泄漏的位置如下图所示的A-D，根据图15所示，测点1测得的压力值较大，且有所延迟，说明泄漏点在测点2附近，泄漏位置则是泄漏点A或B.

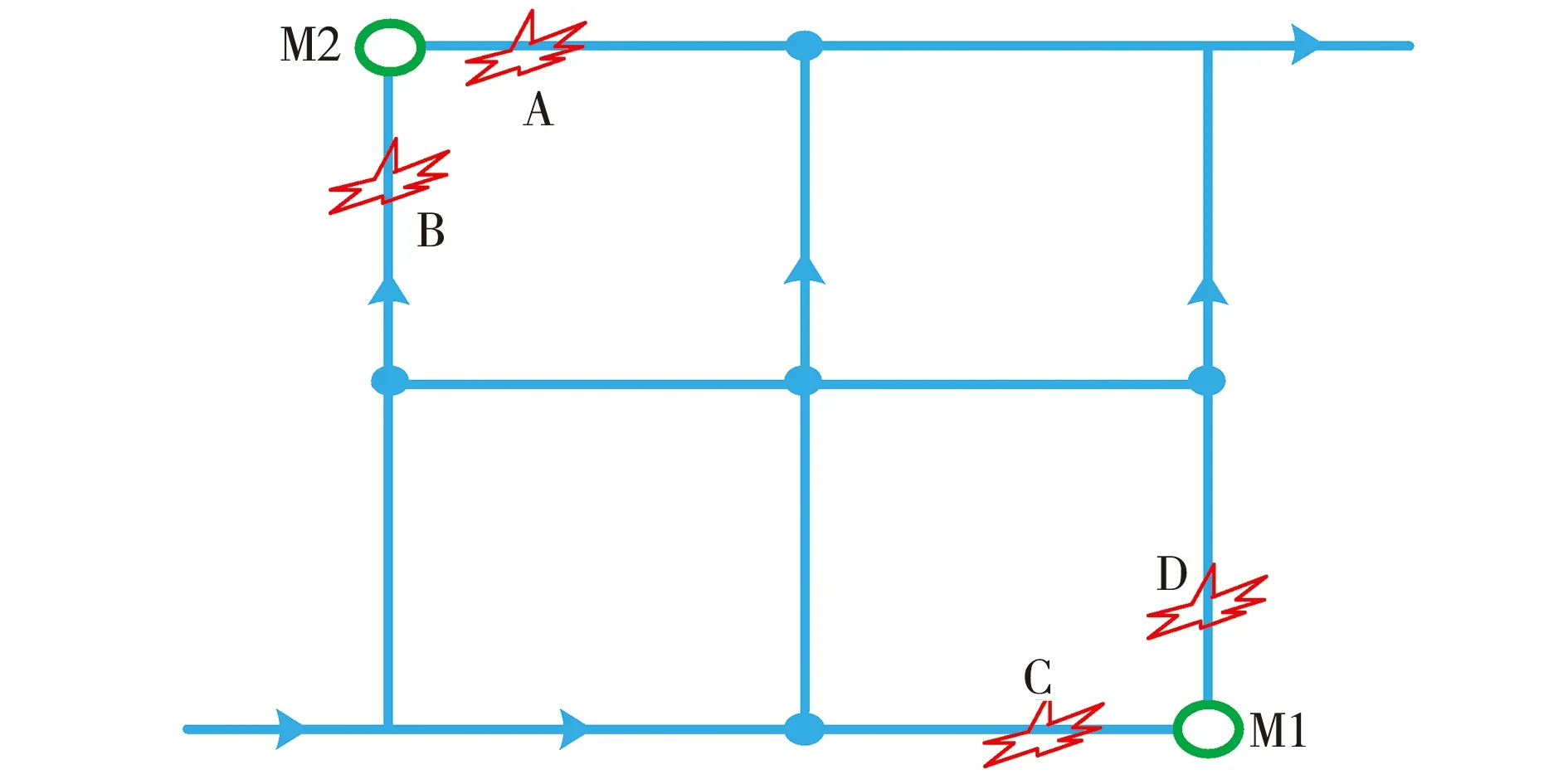
图15 泄漏可能出现位置示意图

因此，为了识别泄漏位置，提出了一种搜索算法.为了排出其他泄漏点，我们采取了新的方案，该方案包括两个特点：它包括环形网络；测量点的排列可以符合试验的要求.这个管道泄漏产生的负压波可以到达压力测量点通过不同的方式，我们可以利用这个特性实验误差分析.具体地：

步骤1：搜索最接近泄漏位置的节点

(12)

公式中：tj、tk为在tj和tk时刻，在节点j和k检测到泄漏瞬变；Si为较小的残值表示泄漏发生在i节点的概率较高；τik为让我们把节点i到k的最短旅行时间表示出来.

假如泄漏在节点i发生，当i=1……N(N=管网中的节点数目)，从而

(tj-tk)-(τij-τik)=0.

(13)

然而，由于时间、测量和其他误差，这个等式的左边永远不会为零.

步骤2：沿着连接到最近节点的管道段搜索泄漏位置.

在这一步骤中，沿着步骤1确定的与节点ni相连的管道部分(即沿着图模型的边缘)放置一组新的虚拟节点.

第一步是对网络中所有节点进行粗略的全局搜索；

第二步在最近的节点估计附近执行本地搜索，以确定沿着管道段的最可能泄漏位置.

此外，管道泄漏产生的压力波传播将通过不同的路径到达测量点，我们可以以A点泄漏时，M1和M2点为例.

图16 A点泄漏时，传递到测点M2的路径

图17 A点泄漏时，传递到测点M1的路径

如图16和17所示，假设A点泄漏，则最符合本次模拟的路线是图16中的(a)和图17中的(b).

表2为根据图14所示的方法计算出的的每个节点的Ei值，由表中可以看出节点3的Ei值最小，节点4的Ei值次之，故离泄漏位置最近的节点为3，并且泄漏位置介于节点3和4之间，泄漏点为点A.根据△t=1.15×10-3s，已知压力波的波速，我们可以求出泄漏点最终确定泄漏位置414 mm，实际泄漏点在431 mm处(泄漏孔1)，在误差允许的范围内，所以该方法可行.

表2 不同节点Ei计算结果

同时，模拟了不同泄漏孔大小和不同进口压力下的5个泄漏点的定位情况，分别进行了30次和20次模拟计算，为了便于分析，取以测点2为起点，传播路径最短的一组数据，现以泄漏孔3和泄漏孔5为例，定位情况如表3、表4所示，误差均在允许的范围内，说明该方法可行.

表3 以泄漏孔3为例的不同泄漏孔的定位情况

表4 以泄漏孔5为例的不同进口压力的定位情况

2.2.4 不同方法及算法对比

2.2.4.1 不同方法对比

由表5可知，近些年现有的检测方法如ITA(Inverse Transient Analysis)，Model Falsification & EPANET，PSO-SVM(Particle Swarm Optimization-Support Vector Machine)等方法的定位能力较高，均在90%以上.本文提到的于反向寻源法定位的准确度在92%～96%之间，在复杂管网的泄漏定位中有一定的应用价值.

表5 不同泄漏检测及定位方法对比

2.2.4.2 算法对比

如图18所示，利用表1中经过网格无关性验证的网格数为442 009的管网模型，在相同的边界条件和参数的设置下，对比了在50 000、100 000、150 000、200 000计算步数下，SIMPLE、PISO及加入伴随方程的PISO算法所需的迭代时间，随着计算步数的增多，三种方式的计算时间均增长.结果表明，SIMPLE算法应用于管网泄漏模拟中，计算速度最慢，伴随方程的PISO算法计算速度最快.

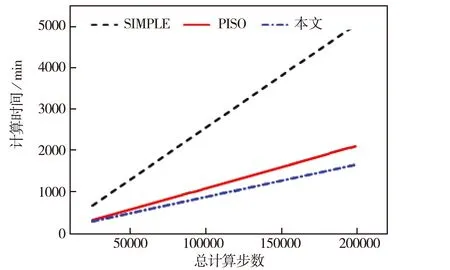
图18 不同计算方法计算速度对比

我们利用了进行了网格无关性验证的管网模型了，进行了一段时间的计算，对比了SIMPLE算法，PISO算法和本文加入了伴随方程的PISO算法，在相同的时间步长下，本文的计算速度明显加快.

2.3 实验验证

在此部分通过对不同漏点进行实验，分析管网中的压力变化规律，将实验数据同模拟结果进行对比分析.以泄漏点1为例，模拟和实验压力变化规律同模拟结果符合度较高.

如图19所示为以泄漏孔1为例的泄漏孔处的压力变化曲线，图中蓝色线条代表压力变化的总体趋势，黑色线条分别为试验和模拟条件下压力变化趋势.从压力变化曲线中可以发现两者变化规律相同，实验数据在泄漏前压力值保持在一个高位水平，泄漏瞬间压力值突降，在到达最底端后，恢复值一个较低的压力值，并逐渐稳定.而模拟数据与实验变化规律相反，这是由于添加了逆向模型的缘故.对比实验和模拟数据，模拟过程阻力小于实验，无噪声的影响，因此模拟压力的最大值高于实验，而泄漏前后的压降大小基本相同.总的来说，从横轴观察泄漏瞬间对应的时间差值可以发现，泄漏是在一瞬间发生的压力变化时间极端，这与模拟的结果相吻合，并且正向压力传播曲线与模拟所得反向压力传播曲线呈现的压力变化趋势相吻合.

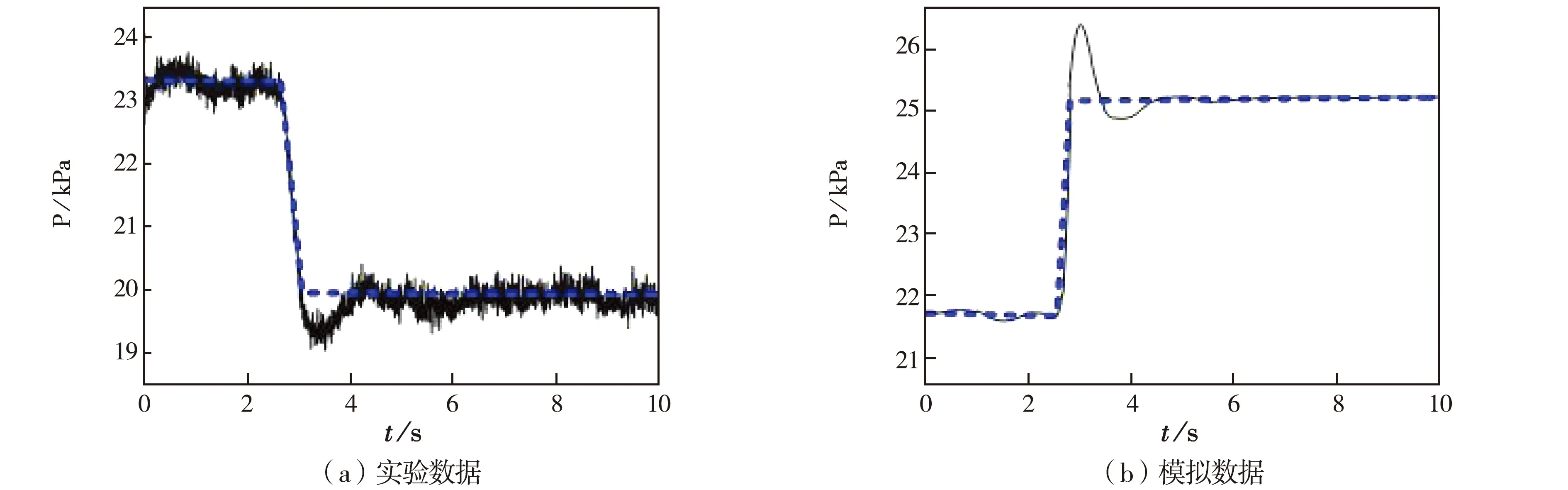
图19 实验模拟对比图

接下来为了进一步验证方法的合理性，对与模拟工况对应的多组实验数据做了处理，将50组实验和模拟的工况进行了计算，对比了各自的定位准确度，如图20所示.

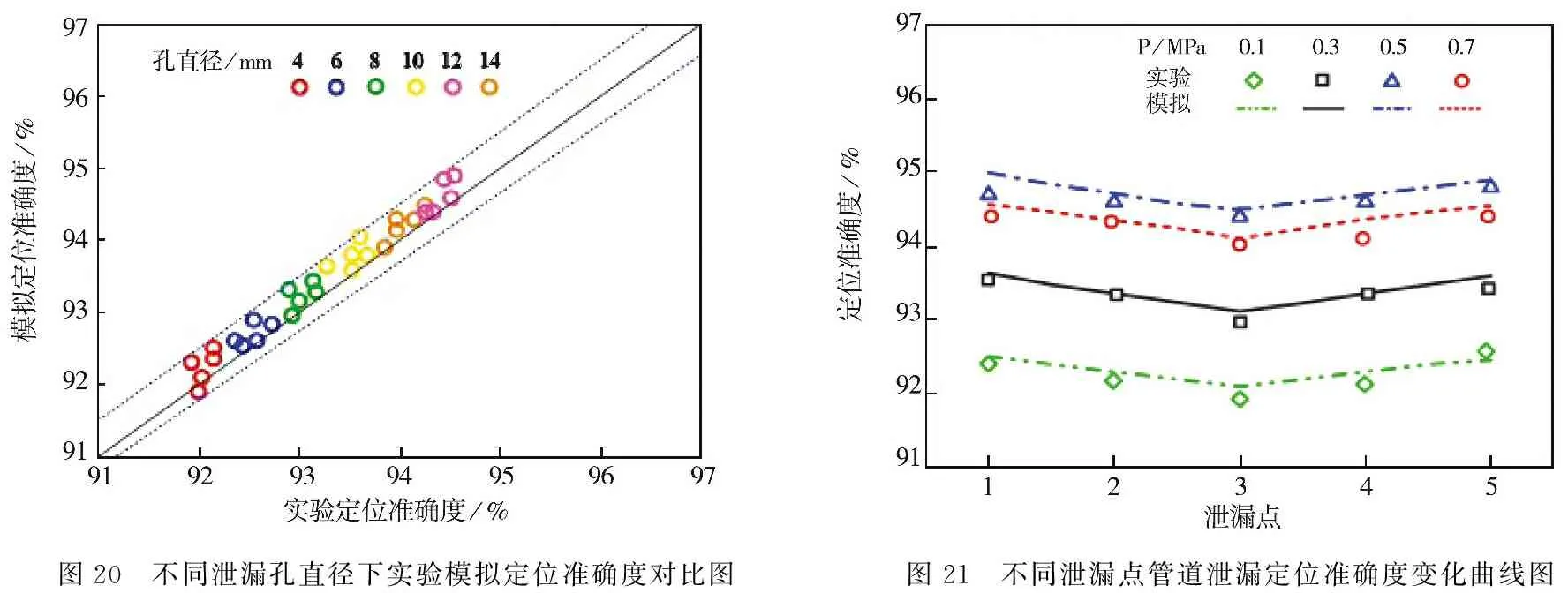
图20 不同泄漏孔直径下实验模拟定位准确度对比图图21 不同泄漏点管道泄漏定位准确度变化曲线图

不同泄漏孔直径下实验模拟定位准确度对比图，如图20所示.可知随着泄漏孔直径增大实验和模拟点位准确度均增大，但当泄漏孔直径达到12 mm时，再增大泄漏孔，由于泄漏孔径很大，泄漏产生的压力波经过两个测点时间很短，时间差计算不准确，进而导致定位位置计算不准确，准确度有所下降.总的来说，实验结果与模拟结果相近，定位准确度在2%左右波动.

不同泄漏点管道泄漏定位准确度变化曲线图，如图21所示.实验管网的形状以及五个泄漏点的位置一定，泄漏点1和泄漏点5距离两个压力测点路径长度一致，定位准确度基本一致，泄漏点2距离测1距离相对较远，误差比1、5大，泄漏点3的定位准确度最低，3点泄漏信号传递到两个压力测点，无论怎样传递都要两次经过四通，并且距离两个测点的长度较长，定位准确度比较低.

总体来说，实验结果与模拟结果基本吻合，均在误差允许的范围内，该方法可行.另外本研究是基于实际管网进行的简化，实际地下供热管网没有四通，多用二个临近三通来代替，压力波的反射情况完全不同，给复杂实际管网检测中带来一定的干扰，但是这种干扰只是增加了一部分计算过程中的局部阻力，压力波传递情况稍有改变，对整体压力变化趋势以及泄漏检测和定位精度影响较小.

3 结 论

本文的主要结合反向寻源原理及伴随方法，推导瞬态流场反向伴随方程.借助MATLAB软件和开源有限元软件OpenFOAM，构建单管和复杂管网流体流动数值模拟模型，在OpenFOAM自定义求解器，将反向寻源问题转化为伴随方程的求解问题.根据得到的图形分析不同测点的压力等参数的变化，结合新时延估计方法和互相关方法，对管网的运行状态进行分析检测，完成对伴随方程的验证和求解，确定泄漏源的可能泄漏位置，最终利用全局搜索方法完成了泄漏源的定位.得出以下结论：

(1)基于正向压力输运模型，引入目标函数，将伴随理论与灵敏度分析方法相结合推导了正向伴随方程.使敏感度函数对压强求导，并引入伴随算子，推导了瞬态流场反向伴随方程，求得了其解析解，并用MATLAB软件，完成了伴随模型的验证，结果证明反向寻源方法可用于管网泄漏检测.

(2)在OpenFOAM中完成了复杂管网流体流动数值模拟模型的构建和伴随方程的求解，并监测了泄漏孔泄漏瞬间压力变化，运用新时延估计方法锐化了峰值点，最后用互相关法进行了相关性分析，发现管道泄漏后，信号相关系数的最大值在零附近有所偏移，通过相关性对比图可知，管道泄漏的出现，最大相关系数的值下降，以泄漏点1为例证明了方法的可行性.

(3)比较了不同泄漏孔大小及不同进口压力下，模拟泄漏定位的准确度，结果表明，运用基于反向寻源法定位的准确度在92%～96%之间，说明此方法可以应用在复杂管网泄漏检测及定位中.

(4)本文在不同计算步数时，对比了单一的SIMPLE、PISO及加入伴随方程的PISO算法所需的迭代时间，结果表明，结合伴随方程的PISO算法的计算速度要明显优于单一的SIMPLE和PISO算法，以此证明了伴随方法的优越性.

在本文中，基于复杂管网泄漏检测及定位模型，未考虑同样引起泄漏的堵塞、变形及污染等问题，应定义相应的求解器，设置相应的参数及边界条件，尽可能将定位方法转化成OpenFOAM语言，便可通过模拟体系，直接得到不同情况下的诊断结果.此外，实验系统存在一定的不稳定性和局限性，与实际复杂管网还有一定差距，只是在宏观上完成了伴随方程的求解和验证，需进一步结合实际工况强化实验和模拟.