航天“Ω”形铝氨槽道热管传热特性分析
2022-09-06路义萍付伟达徐金柱孟柯含
王 斌,路义萍,付伟达,徐金柱,孟柯含
(哈尔滨理工大学机械与动力工程学院,黑龙江 哈尔滨 150080)
热管作为一种高效的传热元件,在建筑、交通、化学、纺织、生产及生活等各个领域得到了广泛的应用[1-2].“Ω”形槽道热管由于截面形状变化而产生毛细力,并利用氨的蒸发冷凝进行热量的传递,具有渗透性强、均温性好等优点,因此在航天领域得到广泛应用[3-4],本文重点研究有无、重力条件下,充液率、底板加热功率对“Ω”形槽道热管的气液两相分布及传热特性的影响.
目前,国内外学者对“Ω”形槽道热管的启动特性及相变传热机制展开研究.Suman[5-6]在考虑基板温度影响时,对V型热管进行数值模拟,提出了新的计算燃烧极限的方法,并推广到任意形状截面的热管,为槽道热管数值分析的进一步深入建立了基础.Zhang[7]建立轴向燕尾型微槽热管的热力和流体力学模型,并进行数值求解,结果表明,蒸发段气液界面的换热系数大于冷凝段.姚峰等[8]建立“Ω”形轴向槽道热管瞬态传热的数学模型,计算结果证明,热管的壁面温度在启动过程中能达到统一的瞬态响应.张程宾[9]对Ω形轴向槽道热管最大传热能力预测,进一步分析讨论了热管结构参数对最大传热能力的影响.Kaimin Yang[10]对热管热特性进行实验和CFD模拟,结果表明随着通道数量的增加,热管的耐热性和最大传热能力呈上升趋势,但等效导热性逐渐降低.杨开敏[11-12]对轴向“Ω”形槽的热管热特性进行实验研究,并使用UDF功能建立热管传热传质模型,结果表明工作温度对热管的等效换热系数影响较大,倾斜角度对等效换热系数的影响不明显.张燕辉[13]等通过VOF模型建立重力热管的数学模型,以水基纳米流体为工质,并编写相变UDF,分析充装率和加热功率对热阻的影响.Anand[14]建立轴向开槽铝-甲烷热管传热性能预测模型,研究液-气界面剪切应力的影响对气液界面半径的轴向变化,并且用单根轴向槽铝甲烷热管来验证模型准确性.Jiachao[15]等利用CFD方法建立完整的二维轴对称物理模型,采用VOF模型,预测传热传质特性.Mansouri[16]建立微通道中轴向传热与传质的数学模型,预测热管的最大换热能力.Aibo Wei[17]利用CFD方法研究了零重力条件下Ω型铝氨槽道热管的流动和传热分析,结果表明随着热流密度的增加,热管的最大温差随之增大,当充液率为25%-35%范围时,热管热阻随填充率的增加而增大.Cotter[18]假设热管内气液相为稳态不可压缩层流,为本文研究指明方向.另外,部分学者[19-20]利用实验研究热管的传热能力.
综上所述,大多数研究都是数值模拟或者搭建实验台测量分析气液两相流动、传质及换热,对于航天重力变化情况下,热管的气液两相分布及传热特性分析研究较少,且地面条件难以实现无重力场条件下的实验,因此本文采用三维数值模拟对于有、无重力环境下的管内气液两相分布流动变化、热阻及传热能力进行详细模拟研究,使用地面实测数据对模型参数进行预测校正,对比总结有、无重力场下不同充液率、底板加热功率下的热管传热特性.
1 模型建立
1.1 几何模型
建立三维“Ω”形槽道热管的物理模型,如图1所示.热管长度L=649 mm,底板宽30 mm,厚度为1.5 mm,槽道个数为20,槽道热管的几何参数见图1.

图1 铝氨槽道热管的物理模型
1.2 网格划分
此模型具有左右对称性,因此建立二分之一模型并进行网格划分,如图2所示.为了保证计算准确性,在槽道及近壁面物理量的梯度变化较大处进行加密处理.

图2 铝氨槽道热管网格划分示意图
2 数学模型
2.1 控制方程
为准确研究管内气液分布和流动情况,选择VOF模型进行计算,可以精确捕捉到交界面相变.在VOF模型计算过程中,为了完整的计算出任何计算单元中不同流体之间的交界面,规定计算域内任何一个控制容积中,所有相体积分数额总和为1,不存在控制容积内不含任何流的情况.假设某一控制单元内存在n相流体,其中第q相流体体积分数为αq,此时控制单元内流体的相体积分数满足的条件[6]为
(1)
当某一控制容积内存在n相流体时,此控制容积平均密度表示为
(2)
在VOF模型中,求解一个或多个相的体积分数的质量守恒方程,对于第q相流体,其质量守恒、动量守恒、能量守恒方程的表达为
(3)
(4)

(5)

(6)
热管的热阻R、蒸发段对流表面传热系数he、冷凝段对流表面传热系数hc分别表示为
(7)
(8)
公式中:Q为蒸发段的热源功率;twe、twc分别为蒸发段、冷凝段平均壁温;Ae、Ac分别为蒸发段和冷凝段的表面积;twa为绝热段平均壁温.
2.2 边界条件及算法设置
在蒸发段底板处设置恒热流密度,冷凝段外壁面设置为恒壁温,绝热段热流密度设置为0,蒸发段热流密度值为施加在热管上的功率与蒸发段面积的比值.
蒸发及冷凝出现在气液交界面处,并考虑表面张力及接触角等对热管的影响,且氨的物理特性(密度、热导率、比热)随着温度、压强等条件发生变化,故对其参数进行拟合,运用多项式插值法进行数值计算,为了准确的模拟初始相位分布,热管内部气液两相流动及传质的过程较为复杂,且离散方法对计算结果的影响很大,因此采用压力-速度耦合方法中的PISO(Pressure Implicit Splitting of Operator),压力差分格式为交错压力格式,对于动量、密度及能量等选用二阶迎风格式,为了准确模拟出交界面的瞬态变化,采用界面重构法对界面进行重构,并运用非稳态过程进行数值计算.
3 结果与分析
3.1 网格独立性验证及计算结果准确性验证
由于网格的质量大小,关乎所求解控制方程的收敛性、计算用时以及模拟出的结果能否准确还原物理现象等方面.对于所研究的热管采用了5套不同的网格数量,且对模拟过程进行监测,稳定运行后,取蒸发段五处壁面的平均温度作为网格独立性的验证标准,如图3所示.从图3看出,随着网格的加密,蒸发段温度不断的减小,计算表格A1到A3的温度变化分别为1.3 K和0.5 K.当网格数量超过A3时,温度的变化率下降的速度变慢.继续增加网格数温度没有明显变化,所以选用1 248 143(A4)网格数量进行计算,既可以得到稳定数值解,又可以节省时间.
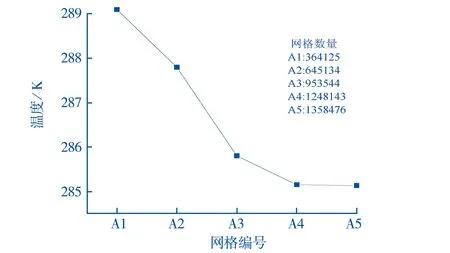
图3 铝氨槽道热管工作温度随网格数量变化
数值模拟设置采用与实验过程中相同的热源功率35 W,冷凝段功率-35 W,此时对应初始压力即饱和压力为6.151 bar,热管为水平放置(沿Z轴方向),重力方向沿y轴负方向,大小为9.8 m/s2.实验时,测点位置分别为8 cm,16 cm,36 cm,46 cm,56 cm处五个测点的温度,地面实验装置[20]如图4所示.

图4 实验装置图
为验证计算模型的精度和可靠性,将对重力场条件下,“Ω”形槽道热管温度分布特征进行数值模拟,并将数值模拟结果与地面实测数据进行对比如图5所示.由图5可知,模拟的壁面温度沿着冷凝方向逐渐减小.与实验相比,误差在0.4 K以内,在误差允许的范围之内.这是因为实验测量存在误差,且测量位置在上方圆柱体,而整体温度分布高温区集中在底板,导致平均温度升高.因此,数值模拟的仿真结果与实验较吻合,该模型轴向温差可以用于分析铝氨热管的基本工作特性,结果可靠,可进行数值计算.

图5 数值模拟结果与实验结果对比
3.2 热管温度分布特征
本文研究有无重力场条件下,7组不同充液率对热管壁面温度的影响,由于部分曲线基本重合,为便于观察,五组不同充液率情况如图6所示.由图6可知,在不同充液率下温度分布变化基本一致,沿轴向温度成阶梯式分布,蒸发段平均温度最高,冷凝段平均温度最低,温度拐点出现在蒸发、绝热及冷凝的交界面处.当充液率为21%时,蒸发段的温度上升趋势变大,热管蒸发段内的沸腾更加剧烈,此时会产生大量的气泡,气泡汇聚在蒸汽腔内以及槽道内形成气液塞,内部有大量的高温气体,隔断了冷凝回流的液体,使蒸发段的气液相不连续分布,使回流受阻,壁温升高,从而可能导致热管蒸发段出现异常情况而失效,故要保证热管的正常工作,充液率应该大于21%.热管存在最佳充液率,初步计算可知,在30%的充液率下,蒸发段与冷凝段平均温差最小,传热性能最好.为了保证热管能在该充液率下正常启动并稳定工作,本文监测热管壁面温度瞬态变化,为研究热管正常工作时的传热特性提供依据.

图6 壁面温度随充液率变化曲线
图7为无重力条件下,21%充液率下蒸发段端部0.05 m截面工质温度随时间变化图,从图7中可知,t=0 s至t=15 s时,蒸发段内部工质温度从283.5 K上升到289 K,温度升高5.5 K,t=15 s时温度不再升高,并且突然下降,是由于冷凝段流体回流所导致,也是热管完成启动循环的标志.t>25 s时,温度继续呈现出有规律的振荡变化,但是整体温度不再有上升的趋势,平均温度保持在288.5 K,振荡幅度为±1 K.热管蒸发段温度并没有达到稳定的数值,而是出现振荡的形式,这是因为此区域的温度较高,热管蒸发段内的工质沸腾更加剧烈,此时产生大量的气泡,气泡汇聚在热管槽道内形成气液塞现象,如图8所示.内部有大量的高温气体,隔断了冷凝回流的液体,使蒸发段的气液相不连续分布,此时气塞内是高温的气体工质,液相内是回流的低温冷凝工质,当不连续的液相流过监测面时会导致温度的上下波动,严重会导致热管失效,故不推荐在该充液率下工作.
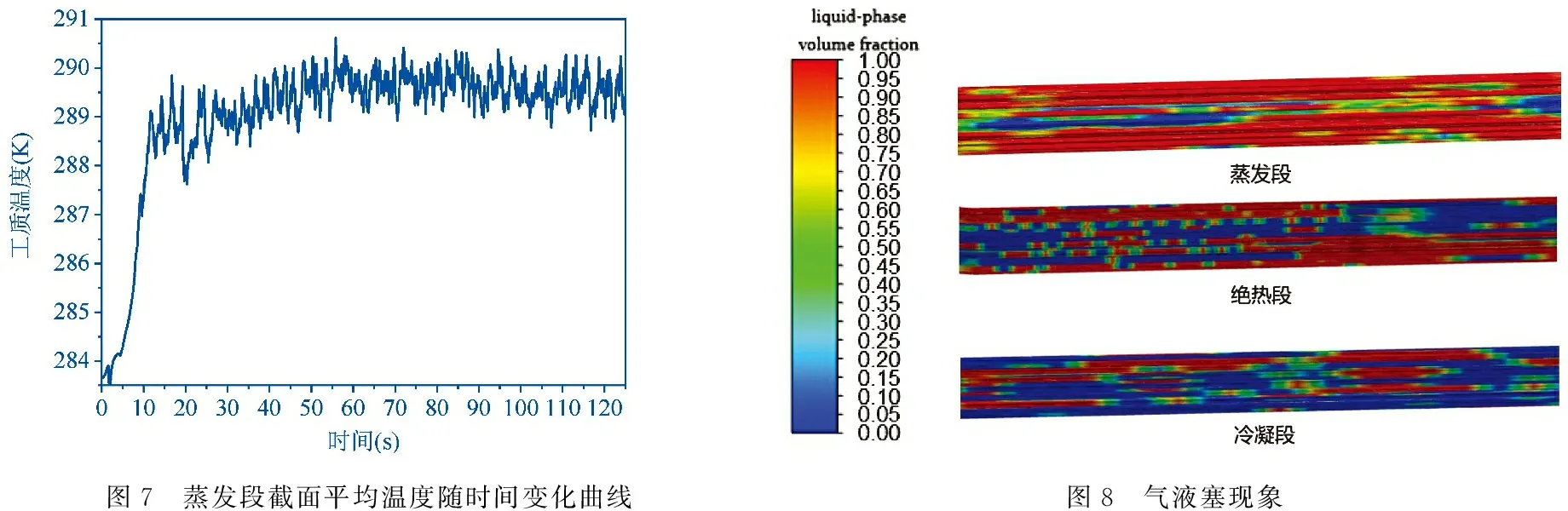
图7 蒸发段截面平均温度随时间变化曲线图8 气液塞现象
3.3 气液分布变化特征
在热源底板加热功率为35 W,冷凝段功率-35 W,充液率为30%时,Z=0.5 m处(冷凝段)XOY截面在t=15 s、25 s、35 s时刻气液两相分布示意图如图9、图10所示.由图9可知,有重力时,气液两相处于上下分层状态,液相聚集在热管气腔底部,形成液池,稳定运行后,大部分槽道内也充满液相,个别槽道内由于气相的存在,压力较大,因此液相分布较少.由图10可知,无重力时,气相充满整个气腔,液相大多位于槽道内,并未在热管底部气腔内形成液池.在有、无重力场条件下,蒸汽均是首先在气腔壁面及窄缝处冷凝形成液膜,并开始汇聚,由于毛细力的作用,液相在由窄缝进入槽道内聚集流动,在蒸发段蒸发,冷凝段冷凝,依次循环往复来传递热量,数值模拟将热管内部的气液两相分布更加直观的展示,如下图所示.
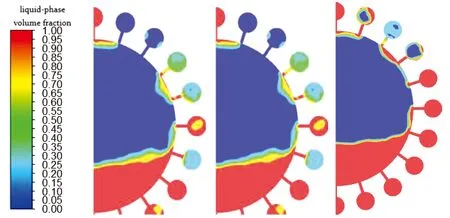
(a)t=15 s (b)t=25 s (c)t=35 s图9 有重力情况下不同时刻冷凝段气液两相分布图

(a)t=15 s (b)t=25 s (c)t=35 s图10 无重力情况下不同时刻冷凝段气液两相分布图
3.4 有无重力条件下热管的传热分析
在理想条件下,“Ω”形轴向槽道热管气液分布的最佳状态为蒸汽充满热管的蒸汽腔,同时回流的液体恰好充满槽道,此时为热管的理论充液率.本文热管蒸汽腔面积为S1=78.54 mm2,槽道面积为S2=1.131 mm2,窄缝面积S3=0.13 mm2,本文研究热管为20个槽道,因此槽道总面积S4=(S2+S3)*20=25.22 mm2,则热管的理论充液率为S4/(S1+S4)=25%,但是应考虑到热管实际不可能按着理性状态运行,一般以理论充液率的1.2倍充装,故本文采用的是30%为基础充液率,研究充液率变化对传热性能的影响,见图11(a)、11(b).
图11(a)显示在热源功率为35W时,有重力场的热阻要大于无重力场条件下的热阻阻值,二者在充液率30%时热阻最小,说明热管传热性能最好,当充液率大于30%,热阻阻值明显有增大趋势.图11(b)显示充液率30%的条件下,当有重力时,随着底板加热功率的增加热管的热阻略有下降,因为受到重力作用,在热管底部形成液池现象,底板加热功率增大,更多的液体工质受热蒸发为气氨,蒸发冷凝段温差减小;当无重力时,加热功率小于45 W时,热管的热阻随功率的增加而减少,当加热功率超过45 W时,热管的热阻随着加热功率的增大而增大,这是由于随着加热功率的增加,液态工质蒸发剧烈,造成局部干烧现象恶化了热管的性能传热,故本文仅研究加热功率小于45 W时的工况.

图11 热阻变化曲线
由图12(a)可知,当热源为35 W,有、无重力场时,充液率从24%增加到30%,二者的对流表面传热系数he随着充液率增大而升高,当热管的充液率达到30%时he最高,整体无重力场条件下he数值高于重力场he数值,因为无重力条件下液氨较均匀分布在槽道参与换热,气氨则均匀分布在整个蒸汽腔内,更加符合理论上热管的工作过程,故热管he增大.图12(b)知,当充液率为30%,有重力条件下,随着加热功率增加he不断增大,he的增加幅度逐渐减小,在无重力条件下加热功率对he大小的影响较大,随着功率的提高,蒸发段温度升高,壁面汽化核心增加,气泡扰动增加,强化换热.但在有重力时随着功率的增加,这种增加的趋势减弱.而无重力时,气化核心对液态工质的扰动更加明显.

图12 蒸发段对流表面传热系数变化曲线

图13 冷凝段对流表面传热系数变化曲线
图13(a)为热源加热功率为35 W条件下,充液率为30%时,有、无重力场状态下冷凝段对流表面传热系数均最大,当热管充液率增加或减小都会使hc降低,但是整体无重力场传热系数大于有重力场.图13(b)为充液率30%条件下,随着功率增加hc升高,二者的hc均呈增大趋势.无重力时,随着底板加热功率的增大,hc的增幅逐渐升高,冷凝段的液膜厚度和积液增加,当加大功率时,更多的高温工质蒸气流向冷凝段,参与相变的工质增多,故换热能力增强.
4 结 论
本文分别在有重力条件和无重力条件下,针对不同底板加热功率及不同充液率的“Ω”形铝氨槽道热管进行气液两相流动及传热的数值模拟.在所研究的充液率范围,底板加热功率范围内,得出以下结论:
(1)有重力时,在热管气腔底部有液氨汇聚形成液池,气腔上部为气相氨,上下分层现象明显,在槽道内及气腔壁面处液氨汇集成股,液膜厚度增加且伴有气液塞现象;无重力时,液氨由于冷凝在槽道及壁面处形成液膜,气相充满整个蒸汽腔,液相大多位于槽道内,并未在热管底部气腔内形成液池,气液两相分布更加合理,接近理想状态.
(2)当热管充液率为30%充液率时,热管热阻最小,对流表面换热系数最大,传热性能最好.
(3)底板加热功率建议在15 W到45 W内,该区间内对流表面传热系数随加热功率的增大而增加,45 W时传热性能最好.
(4)无重力条件下的热管整体传热性能比有重力条件情况提升5%~20%.
