回转体高速入水载荷的数值计算研究

王禹开，王 璐，刘平安

(哈尔滨工程大学航天与建筑工程学院，黑龙江 哈尔滨 150001)

近年来世界各国由于对科技发展的急切渴望以及对各类资源的迫切需求，海上资源和领土的争夺日益升温.尤其是能源资源短缺越来越严重，在这样的背景下，各国对海洋资源的争夺更加激烈，相互之间很难做出让步、妥协.

“入水”现象在海上十分常见，在军工装备科技领域如深水炸弹、空投鱼雷、水上飞机、破障炮、航天飞行器的回收、反潜武器和跨介质飞行器等诸多方面都有实际应用[1-6].入水过程从运动体头部触及自由水面瞬间开始，在触点附近水域产生一个使水域流动的扰动，扰动在水域中迅速向四周传播，随着时间的推移，运动体进入到水域中达到稳定状态完成入水过程.而在运动体与自由液面相接触时，尤其是高速入水条件下的接触瞬间，运动体会受到极大的砰击力的作用，虽然砰击力的作用时间很短，但是这种强大的载荷可能会导致运动体结构损伤.故为了实现安全有效的高速入水，首先需要研究运动体入水载荷的相关影响因素及变化规律.

运动体入水初期开始于诸多学者的实验研究，Thompson[7]对水上飞机降落的受到的最大压力进行了实验研究.Wagner[8]在VonKarman的基础之上进一步考虑了撞击水面时自由液面的升高现象，提出了小斜升角模型的近似平板理论.孙明根等[9]通过高速摄影的方法，对几种简单的线形弹头垂直入水的情况进行了实验研究，测得了模型在入水时的加速度并且观察了其入水时的运动状态.

在数值仿真方面，人们从平板等简单模型入手，逐渐进行更加深入研究.易文俊分别利用FLUENT和SCAV软件在小攻角下对水下高速炮弹的超空泡流场进行了仿真计算[10-11]，得出射弹的航行攻角显著的影响超空泡形态的轴对称性.徐胜利等[12]采用纹影、阴影流场显示的方法对弹体的倾斜入水进行了实验研究，观察到了弹体倾斜入水过程中流场变化.

目前国内对入水问题的研究较多关注于垂直入水问题，针对入水空泡、入水弹道等发展变化过程往往做定性分析.本文在垂直入水的计算基础上进一步对有角度入水的弹体载荷进行计算，并通过对弹身不同部分的划分计算，详细的对弹体入水载荷变化进行了对比分析.

1 计算方法

1.1 VOF多相流模型

VOF模型可以实现对运动相界面的追踪，通过对整个求解流域内进行计算，以每一个网格单元定义相函数，以得到每一个所需求解网格内介质种类定性和定量的分析，VOF方法的控制方程与其他计算流体力学方法有相似之处，它是通过求解多相的一个连续的体积分数方程来完成的.对于第q相，其方程[13]为

(1)

(2)

体积分数方程可通过下述隐式或显式方程求解：

欧拉显式方程

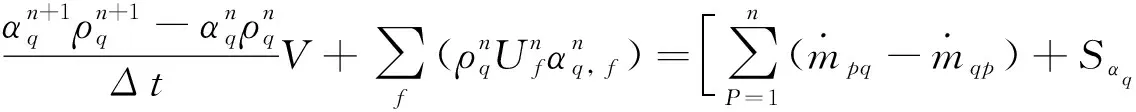
(3)

隐式方程

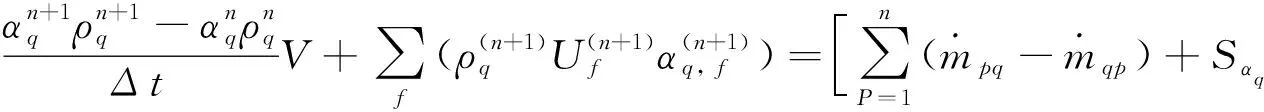
(4)

公式中：n+1为新时间步长的指针；n为前一时间步长的指针；αq， f为一阶迎风、二阶迎风，算法中的第q相体分数的数值；V为单元的体积；Uf为以法向速度通过面的体积流量.

控制方程

(1)连续方程

(5)

(6)

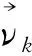
(2)动量方程

(7)

公式中：P为压力；S为源项[14]；τij为剪切应力；τij的计算式为

(8)

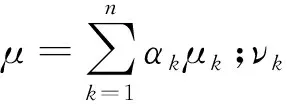
(3)能量方程

(9)

公式中：keff为有效热传导；Sh为源项；T为温度；E为能量，其中E采用平均变量为

(10)

1.2 湍流模型

标准k-ε两方程模型对于解决弯曲壁面和弯曲流体的问题有所缺陷，而且其在时均应变率比较大的时候，有可能导致负的正压力.而Realizablek-ε模型为了使流动更加符合湍流规律，对正应力进行了某种特别的约束，这种约束主要是让计算式中的系数Cμ不再以常数的形式存在，而是与应变率联系起来.Realizablek-ε模型较标准k-ε模型相比能够更加有效的用于各种复杂的湍流仿真计算，包括弯管内流动、带旋转的剪切流流动以及分离流流动.

综上所述，Realizablek-ε湍流模型所具有的特点最符合所需，故选用Realizablek-ε湍流模型，其相关控制方程[15]如下：

k和ε的运输方程：

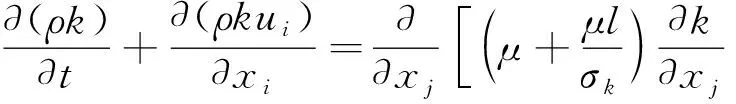
(11)

(12)

公式(12)中：

(13)

公式(12)中，μt与Cμ按下式计算为

(14)

公式(14)中：

(15)

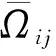
1.3 空化模型

本文所研究的弹体入水速度较高，入水时存在空化现象，采用基于Rayleigh-Plesset气泡动力学方程的Schnerr-Sauer空化模型，该模型将气体和液体的混合物当做含有大量球形气泡的液体来处理，其凝结率和汽化率大致一样，相关控制方程为

Schnerr-Sauer空化模型的相关控制方程[16]如下：

(16)

(17)

(18)

公式中：RB为气泡直径，其计算式为

(19)

公式中：n为气泡的数密度.

2 计算方案

2.1 计算模型

在弹体入水的过程中，弹体载荷会在各个方向表现出一定差异并呈现出一定规律性，在弹体本身的各个不同部分其载荷也有很大差别.为了能对弹身各部分载荷变化规律进行详细分析，本文将弹体进行分块，如图1所示，分为空化器部分(body1)，锥体头部(body2)，柱体弹身部分(body3)，后体部分(body4)四个大块，每个大块又分为迎水侧和背水侧两部分，共8个小部分，具体尺寸如图2所示.

图1 弹体模型分割示意图

图2 弹体尺寸图(单位：mm)

2.2 计算设置

本文数值仿真计算采用VOF多相流模型，Realizablek-ε湍流模型，Schnerr-Sauer空化模型，在第2节中已详细叙述不再赘述.除此之外，六自由度求解器对于在流场中运动的刚体的加速度的计算比较精确，对于作用在流体中刚体的受力和力矩的计算也较为理想，所以本文采用六自由度求解器模型对弹体的运动进行描述.

计算所用边界条件如图3所示，为了避免在入水数值计算的过程中壁面发生条件反射背景区域的上面、下面、左面、背面均设置为速度入口.为了减少数值计算的工作量，由于弹体模型为一个三维回转体，所以本文以弹体轴截面为分割面将其分割为两半，只对其中半个弹体进行数值计算.因此，背景计算区域也以弹体轴线分割面分成两半，将该分割面定义为对称面.背景区域右侧定义为压力出口，背景区域其他边界均设置为速度入口.前侧边界条件选定为对称平面，其理由也是为了只计算以弹体轴向截面为分割面的一半区域，以减少网格数量，减少计算时间提高计算效率.由于弹体为一密闭刚体，所以弹体表面边界条件均选定为无滑移壁面.其余为重叠网格区域，其边界条件均设为重叠网格.

图3 计算边界条件示意图

3 计算结果分析

3.1 网格无关性验证

分别对三套不同网格(网格数分别约为：40万、90万、200万)进行计算，因为高速入水时入水瞬间的冲击载荷为整个计算过程的重中之重，故提取三套网格的撞水峰值载荷计算结果如下表所示，由表中可以看出当网格数从90万提升至约200万时，其峰值载荷变化不大，仅为0.20%，综合考虑计算的时间因素，本文采用网格数约为90万.

表1 网格无关性验证结果

3.2 垂直入水过程及载荷分析

根据100 m/s垂直入水的数值仿真结果，弹体入水全过程如图4所示.对整个入水过程分析如下：

(1)弹体由空气中运动至临近气液交界面，水面开始有轻微波动，体现出气垫效应；

(2)弹体头部逐渐深入液面之下，与此同时，弹体表面开始出现空泡，空泡从头部开始向后将弹体在液面之下的部分包裹在内；

(3)弹体在完全进入水中后水面不会马上闭合，处于开空泡阶段；

(4)随着弹体深入水中空泡长度继续增长，水面慢慢开始闭合；

(5)空泡趋于稳定，水面和空泡尾部基本闭合，进入水下航行阶段.

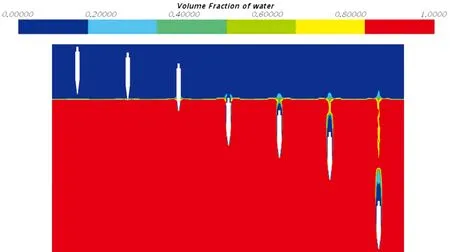
图4 垂直入水过程液相图

100 m/s、150 m/s和200 m/s速度垂直入水弹体的液相图，如图5所示.通过对比可以看出，当其他条件保持相同时，随着弹体速度的增大弹体在水中航行阶段的初期空泡长度和大小明显增大，同时，空泡闭合更晚，后激水花更为明显.

图5 不同速度垂直入水液相图

根据计算结果，入水载荷的变化如曲线图6所示，对其分析如下：

(1)弹体在与水面接触之前，其载荷主要来自于高速运动使得弹体头部压缩空气产生高压区，尾部产生低压区，从而产生的压差阻力；

(2)当弹体与液面相接触时，弹体头部撞水过程时间极短，瞬间产生了一个极大的载荷峰值.瞬间载荷峰值分别达到了185.38 N、368.24 N和444.49 N，分别是弹体撞水前所受载荷的4 838.00%、5 324.78%和5 356.59%.100 m/s速度弹体的撞水载荷峰值仅为150 m/s弹体撞水载荷峰值的50.34%，150 m/s速度弹体的撞水载荷峰值仅为200 m/s弹体撞水载荷峰值的82.85%；

(3)在弹体卸载过后，水下弹身被空泡包裹，所受的载荷主要来自于头部，由于头型相同载荷变化趋势相近，其波动主要来自于空泡演化和弹身不同部分与水体的先后接触；

(4)弹体完全入水之后，弹体所受载荷逐渐趋于平稳，如图7所示，通过与文献中实验曲线[9]对比，其呈现相同的变化趋势，载荷的峰值大小差异是由速度条件差异造成.

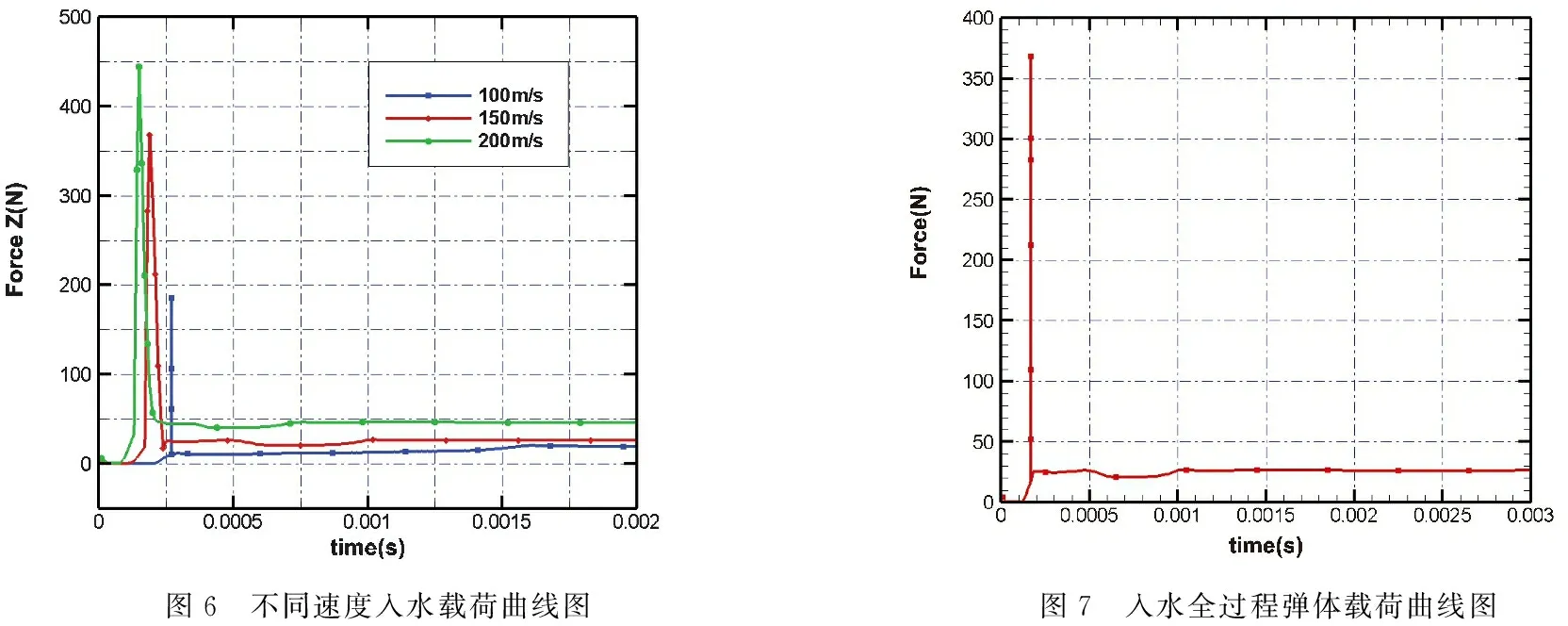
图6 不同速度入水载荷曲线图图7 入水全过程弹体载荷曲线图

3.3 斜入水过程及载荷分析

弹体30°入水和60°入水过程如图8和图9所示.发现弹体与水面相撞时头部两侧水面出现水花，其中弹身迎水侧水花较小，背水侧水花较大，且水花与弹身之间的距离也呈现为迎水侧水花紧贴弹身，而背水侧水花远离弹身.除此之外，通过不同入水角度弹体之间的对比可以发现，当入水角度减小时这种现象越发明显，弹体逐渐入水过程中，弹身两侧水面水花逐渐增大，弹体背水面的水花会向远离弹身侧流动，这种现象将使得斜入水弹体除头部空化器表面外，其迎水侧受载也会很强，更易引起结构损伤.同时可以看出，平头弹体在入水过程中弹道较为稳定，在入水初期不易发生明显的弹道偏移现象.

图8 弹体30°入水液相图

图9 弹体60°入水液相图

弹体斜入水时其载荷特性如图10所示，发现斜入水时载荷峰值和变化规律与垂直入水存在明显差异，根据计算结果具体分析如下：

(1)弹体的载荷峰值随入水角度变化呈现出一些规律，其中90°入水的弹体轴向载荷远大于其他角度入水的轴向载荷，其撞水载荷的峰值为60°入水的140.07%，为30°入水的163.04%，载荷峰值随入水角度的减小而减小；

(2)弹体各部分的压强载荷特性如图11所示，发现弹体与液面接触前，各部分压强载荷较小.body1前压强略高于大气压强，body1l部分压强始终高于body1r部分压强.body2、body3的各部分也都存在相似的情况，而body4两侧存在低压区，这是由尾部的几何形状造成的尾部低压区；

(3)在弹体撞水瞬间，其body1出现压强载荷峰值，头部body1的压强瞬间增加到了107数量级，且body1l压强明显比body1r压强高，其中body1l峰值平均压强为16 349 564.15 Pa，body1r峰值平均压强为13 476 740.75 Pa，为body1l平均压强的82.43%；

(4)随着弹体逐渐入水卸载，body1的压强载荷下降至106数量级并逐渐趋于稳定；

(5)在弹体完全入水之后，body1两侧的l和r部分的压强载荷仍呈现出l侧比r侧更大；body2，body3，body4三部分的平均压强同样呈现出l侧比r侧更大，然而其平均压强较body1相比要低得多，这是因为弹体在水下航行阶段其弹身被空泡完全包裹，弹身周围均处于空泡内的低压区，而body1前端与水相接处，故其平均压强与其他部分相比较高.由此可见，其他部分由于空泡的保护压强较小，在水下航行阶段承担大部分载荷的仍是弹体头部前缘空化器部分.

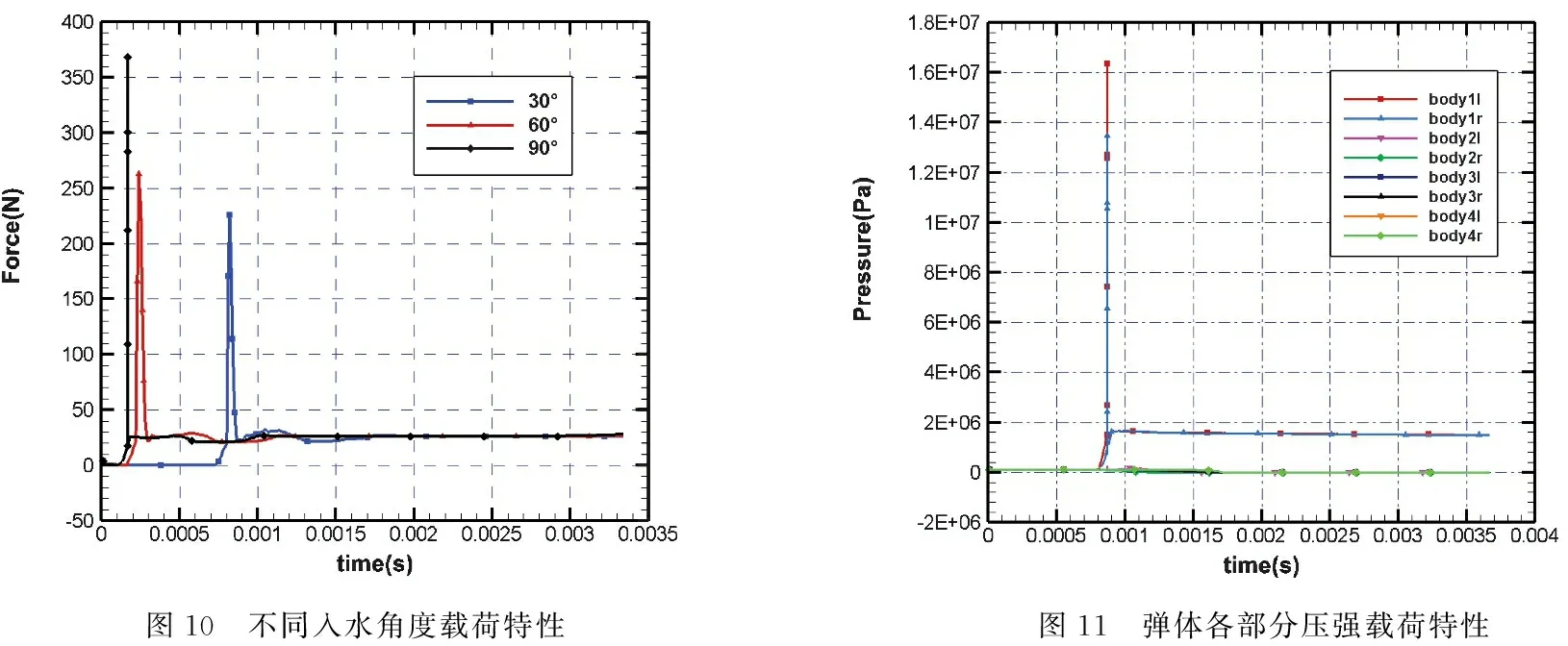
图10 不同入水角度载荷特性图11 弹体各部分压强载荷特性

4 结 论

本文以三维回转体弹型为计算对象，借助Star-CCM+软件平台，采用重叠网格技术；使用VOF模型捕捉气液交界面，Schnerr-Sauer模型描述弹体周围的空化过程；运用六自由度求解器对弹体运动过程中的受力、力矩和加速度等进行计算.详细的讨论了不同速度条件下垂直入水过程及载荷变化规律，并进一步将弹身进行分割并讨论了不同入水角度条件下弹体入水过程及整体载荷和弹身各部分载荷变化规律，得出以下结论：

(1)弹体在入水之前的空气中运动阶段，其运动状态较为稳定，载荷较小，对弹体结构产生的影响几乎可以忽略.

(2)撞水瞬间会在弹体头部产生极强的冲击载荷，其压强载荷峰值可达撞水前的数百倍以上，本文弹体模型条件下轴向受力载荷峰值可达撞水前的50倍以上.

(3)在弹型和其他初始运动参数相同的条件下，弹体载荷受速度影响极大.在本文选取计算的速度中100 m/s入水载荷峰值仅为150 m/s入水载荷峰值的50.34%，150 m/s入水载荷峰值仅为200 m/s入水载荷峰值的82.85%.

(4)弹体在斜入水时，受载随入水角度减小而减小，其头部前缘空化器部分与垂直入水时一样为受载主体，然而斜入水时头部受载极其不均，迎水侧受载明显高于背水侧，更容易引起弹体损伤.